字符串学习笔记
今天重新拾起字符串。其实本来早就学过的,但是早就忘光了。所以复习一下,笔记记在这里,以免自己以后再忘掉。
字符串哈希
什么是字符串哈希
将某个字符串压缩成一个数字的方法。
设字符串为 \(S\)。其对应的唯一的哈希值为 \(\mathrm{hash_{S}} = \sum \limits_{i = 1}^{|S|} S_i b ^ {|S| - i} \bmod P\)。也就是对应了一个 \(b\) 进制的数。
对于哈希有两条性质:
-
哈希值不同的两个字符串一定不相等。
-
哈希值相同的两个字符串不一定相等。这也就是所谓的哈希冲突。
哈希冲突的概率与 \(P\) 的大小成反比。因此需要选择大质数来做模数,以避免哈希冲突。
如何求字符串哈希
按照定义模拟即可。时间复杂度 \(\Theta(|S|)\)。
如何求子串哈希
假设要求子串 \(S[l \sim r]\) 的哈希值。设 \(S[1 \sim r]\) 的哈希值为 \(\mathrm{hash_r}\),\(S[1, l - 1]\) 的哈希值为 \(\mathrm{hash_{l - 1}}\)。那么可以看出,\(\mathrm{hash_{r}} = \sum \limits_{i = 1}^{r} S_i b ^ {r - i}\), \(\mathrm{hash_{l - 1}} = \sum \limits_{i = 1}^{l - 1} S_i b ^ {l - i - 1}\)。因此求子串哈希 \(\mathrm{hash_{S[l, r]}} = \mathrm{hash_r} - \mathrm{hash_{l - 1}} \times b ^{r - l + 1}\)。
其他技巧
-
由于取模需要很长时间,在实现过程中可以用
unsigned int或unsigned long long来存储哈希值。由于unsigned有自动溢出的特性,这样相当于自动对 \(2 ^ {31} - 1 / 2 ^{64} - 1\) 取模了。 -
如果担心有人卡哈希,可以尝试一下换个模数或者写双哈希。
哈希模板:
struct hash_string {
string S; int mod, p;
vector<long long> h;
vector<long long> p_pow;
hash_string() {}
hash_string(int mod, int p):mod(mod), p(p) { p_pow.emplace_back(1ll); h.emplace_back(0ll); }
hash_string(string S, int mod, int p) : S(S), mod(mod), p(p) { // 初始化字符串和模数
p_pow.emplace_back(1ll); h.emplace_back(0ll);
for (auto c : S) {
h.emplace_back((h.back() * p + c) % mod);
p_pow.emplace_back(p_pow.back() * p % mod);
}
}
void insert(char c) { // 插入字符
S += c; h.emplace_back((h.back() * p + c) % mod);
p_pow.emplace_back(p_pow.back() * p % mod);
}
int hash_value(int l, int r) { // 查询哈希值
return ((h[r] - h[l - 1] * p_pow[r - l + 1] % mod) % mod + mod) % mod;
}
};
struct double_hash {
string S; hash_string hash1, hash2;
double_hash() {}
double_hash(string S) : S(S) { // 初始化。传入字符串,哈希模数为原定。
hash1 = hash_string(S, (int)1e9 + 7, 1331);
hash2 = hash_string(S, (int)1e9 + 9, 1331);
}
double_hash(string S, int mod1, int p1, int mod2, int p2) : S(S) { // 初始化,传入字符串和哈希模数
hash1 = hash_string(S, mod1, p1);
hash2 = hash_string(S, mod2, p2);
}
bool equal(int l1, int r1, int l2, int r2) { // 判断两段串是否相等。
return (hash1.hash_value(l1, r1) == hash1.hash_value(l2, r2) and
hash2.hash_value(l1, r1) == hash2.hash_value(l2, r2));
}
void insert(char c) { // 插入字符
hash1.insert(c), hash2.insert(c);
}
};
例题
\(\text{P3805 【模板】manacher 算法}\)
线性时间内求出最长回文子串。
显然,这道题需要用 \(\text{manacher}\) 算法来做。但是哈希也可以线性水过。
- \(O(n ^ 2)\) 算法
先求一遍正反哈希,然后枚举回文中心。再枚举回文长度 \(k\)。这里的 \(k\) 是指回文中心前后相同的长度都为 \(k\)。然后在用哈希判断是否相等。
这样只能解决奇串?分讨或者在中间加空白字符就好了嘛。
- \(O(n \log n)\) 算法
\(O(n ^ 2)\) 的枚举回文长度改成二分即可。
- \(O(n)\) 算法
考虑设 \(Ans_i\) 表示以 \(i\) 为结尾的最长回文子串。易得 \(Ans_i \le Ans_{i - 1} + 2\)。因此计算 \(Ans_i\) 时从 \(Ans_{i - 1} + 2\) 开始倒序枚举至合法即可。
感性的理解复杂度:如果每次 \(Ans_i = Ans_{i - 1} + 2\) 就非常好。如果每次 \(Ans_i < Ans_{i - 1} + 2\),那么每次需要暴力循环至少 \(1\) 次才能找到最长回文子串。这看似是 \(O(n ^ 2)\) 的。但是实际上,由于 \(Ans_i\) 恒大于零这个限制,可以发现最多暴力匹配 \(2n\) 次。
因此如果考场上忘了怎么写马拉车,也可以直接写哈希艹过。
ULL get_hash(int l, int r, int op) {
if (op == 1) return (h1[r] - h1[l - 1] * p[r - l + 1]);
if (op == 2) return (h2[l] - h2[r + 1] * p[r - l + 1]);
}
bool check(int now, int pos) { // 以 i 为右端点的长度为 now 的回文子串是否存在
if (now > pos) return false;
int k = now >> 1;
ULL A = get_hash(pos - k + 1, pos, 1);
ULL B = get_hash(pos - now + 1, pos - now + k, 2);
return A == B;
}
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
p[0] = 1;
for (int i = 1; i <= n; i ++ ) {
h1[i] = 1ull * h1[i - 1] * P + s[i];
p[i] = 1ull * p[i - 1] * P;
}
for (int i = n; i >= 1; i -- )
h2[i] = 1ull * h2[i + 1] * P + s[i];
ans[1] = 1;
for (int i = 2; i <= n; i ++ ) {
int now = ans[i - 1] + 2;
while (now != 1) {
if (check(now, i)) break;
now -- ;
}
ans[i] = now;
}
}
原本把子序列看成子串了,还以为这个紫这么简单。
首先将 \(a\) 哈希一下。然后考虑每次加 \(x\),原数列变成 \(\{ a_i + x\}\),它的哈希变成 \(\sum \limits_{i = 1}^{n} (a_i + x) \times p ^ {n - i} = \sum \limits_{i = 1}^{n} a_i \times p ^ {n - i} + x \sum \limits_{i = 1}^{n} p ^ {n - i}\)。设 \(s = \sum \limits_{i = 1}^{n} p ^ {n - i}\),则新的哈希就是原哈希 $ + xs$。
枚举 \(x \in [0, m - n]\),计算出 \(\{ a_i + x\}\) 的哈希并存储。可以搞个 map / unordered_map 之类的存。
接下来该解决 \(b\) 序列的匹配问题了。考虑到 \(a\) 是一个排列,那么 \(b\) 的合法子序列一定是排序后连续的。考虑将 \(b\) 按照权值排序,然后按照权值插入空序列,插入位置为其在原序列位置,即保持原偏序不变。然后每插入一次求一边当前哈希,看看 map / unordered_map 中有没有对应的 \(a\) 序列。如果当前序列 \(b\) 构造的新序列长度大于 \(n\),那么就删除新序列中权值最小的点。
要求支持插入和删除操作,显然一个权值线段树就能搞。由于平衡树太难写了,所以我拿权值线段树实现的。时间复杂度 \(O(n \log n)\)。我在这里假设 \(n, m\) 同阶。
卡哈希卡了好久,最后发现直接开 unsigned long long / unsigned int 自然溢出就可过。
kmp 算法
-
\(\text{border}\) :一个字符串的最长相等前后缀。
-
模式串:
较长的那个串 -
模板串:
较短的那个串
假设模式串长度为 \(n\),模板串长度为 \(m\)。
首先考虑暴力做法:每次将模板串往前挪一位,然后看看匹不匹配。时间复杂度 \(O(n \times m)\)。
接下来考虑优化这个算法:字符串哈希 \(O(n + m)\)。
字符串哈希有一定的错误概率,这就是学习 \(\text{kmp}\) 算法的意义了。
首先考虑首先考虑下面这个例子:
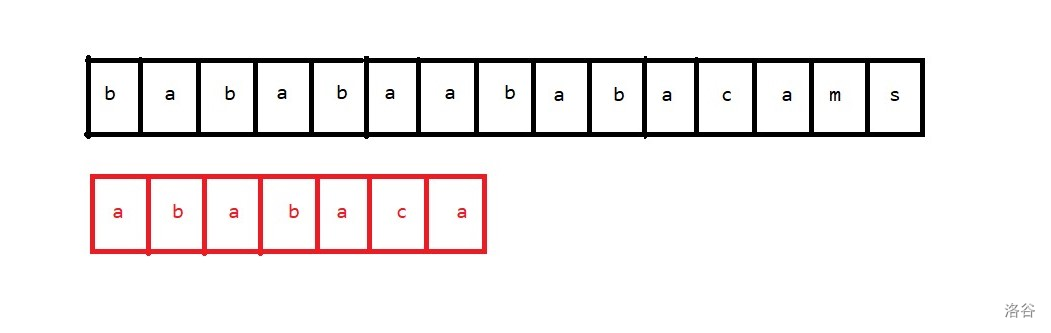
上面的串是模式串 \(s\),下面这个串是模板串 \(p\)。
首先要求出模板串每个前缀串的 \(\text{border}\),记为 \(next_i\)。然后考虑每次失配。假设是下面的情景:
\(\text{We can assume that it's been this situation:}\)
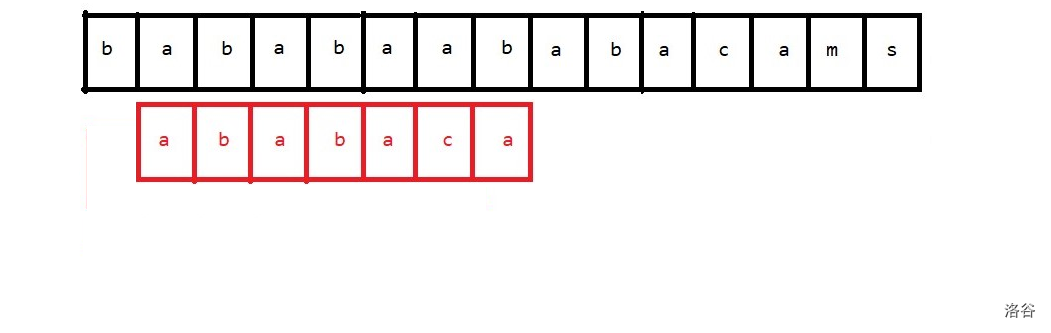
现在在模板串的第 \(6\) 的字符失配了。应该是 \(\texttt{c}\),但是匹配到了 \(\texttt{a}\)。
如果按照原来的暴力,就需要这样移动:
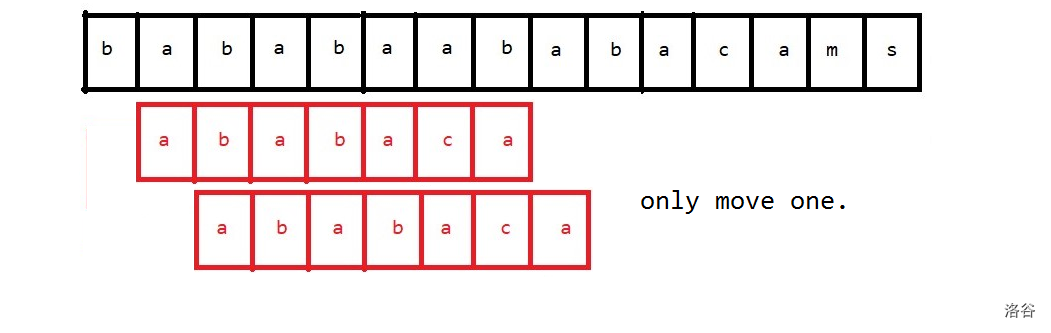
但是这样第一个字符明显是无法匹配的,这样白白浪费了时间。
因此考虑像这样移动:
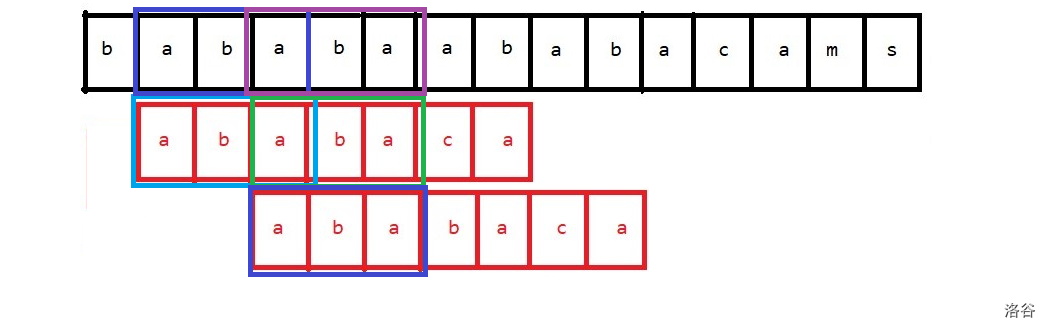
我拿彩色框框框起来的都是相同的子串。可以看出,这样前三个字符是一定匹配的。这样就很优秀。
也就是说,我们要首先找到 失配字符之前的子串最长相同前后缀,然后把模式串的前缀移动到和后缀匹配起来。
也就是说像下面的情景:
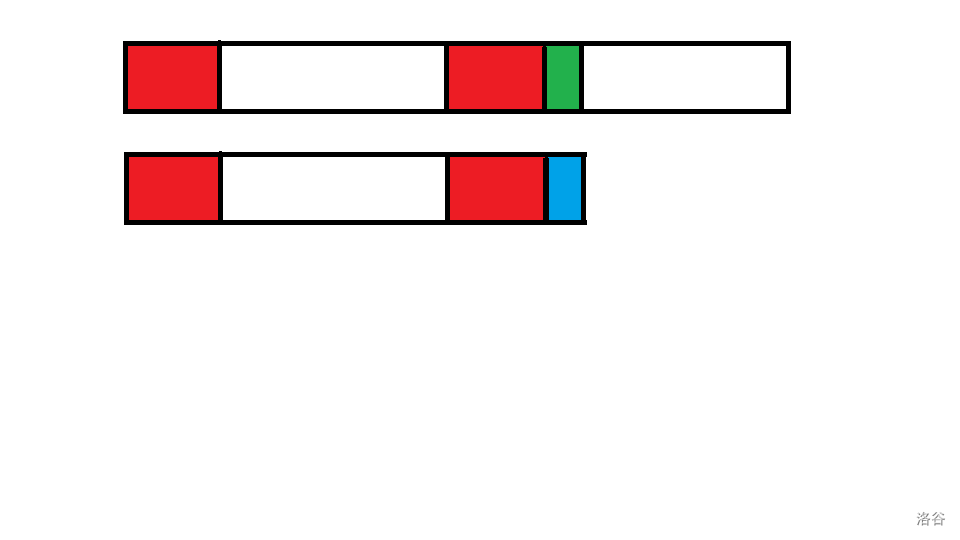
现在红色的串都相等,蓝色的字符和绿色的字符是第一个失配的字符。那么需要这样移动:
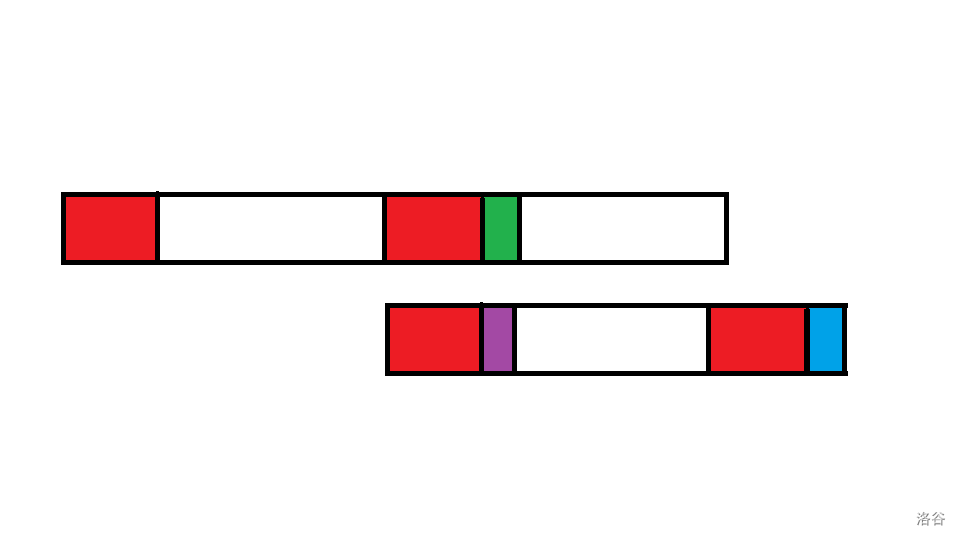
可以看出,现在第一个串的第二个红色段和第二个串的第一个红色段还是匹配的,这样就省了许多移动。现在就只需要比较绿色和紫色字符是否一样就行了。如果不一样,继续按照上面的说法,求出红色串的 \(\text{border}\),然后重复操作就可以了。
如何证明复杂度是 \(O(n)\) 的?不会。大概是因为短串单调右移?
char s[N], p[N];
int n, m, ne[N];
int main() {
scanf("%s", s + 1); // s 为模式串
scanf("%s", p + 1); // p 为模板串
n = strlen(s + 1), m = strlen(p + 1);
for (int i = 2, j = 0; i <= m; i ++ ) {
while (j and p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j; // ne 存的是每个前缀串的 border
}
for (int i = 1, j = 0; i <= n; i ++ ) {
while (j and s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m) {
printf("%d\n", i - m + 1);
j = ne[j];
}
}
for (int i = 1; i <= m; i ++ )
printf("%d ", ne[i]);
}
字典树 trie
允许使用单次 \(O(|T|)\) 复杂度匹配多字符串的算法。
从根节点开始,每个节点指出大小为字符集的出边。没什么好说的,一万年以后我也会。
建议用指针建,省空间。
struct node {
bool end, repeaten;
node *s[26];
node() {
end = false, repeaten = false;
for (int i = 0; i < 26; i ++ )
s[i] = nullptr;
}
}*root;
void insert(node *u, string str) {
if (str.empty()) { u -> end = true; return; }
int c = str[0] - 'a'; str.erase(str.begin());
if (u -> s[c] == nullptr) u -> s[c] = new node();
insert(u -> s[c], str);
}
string query(node *u, string str) {
if (str.empty()) {
if (!u -> end) return "WRONG\n";
if (u -> repeaten) return "REPEAT\n";
u -> repeaten = true; return "OK\n";
}
int c = str[0] - 'a'; str.erase(str.begin());
if (u -> s[c] == nullptr) return "WRONG\n";
return query(u -> s[c], str);
}
01 trie
不想写了,反正会写。也就求个最大 \(\operatorname{xor}\) 和。
思路大概就是根据异或的性质进行贪心。
AC 自动机
\(trie\) 上的 \(kmp\)。对于每个节点 \(x\) 建一个 \(fail\) 指针,它指向的点 \(y\) 到根的路径组成的字符串 \(S_y\) 是 \(S_x\) 的最长后缀。匹配的复杂度为 \(O(|S|)\),但是建立 \(\text{fail}\) 指针的复杂度是错误的。
Fail 树
将 \(fail\) 边都抽出来发现是树形结构。每个节点到根路径上的点均为其后缀。每个节点的父亲都是他的最长后缀。
然后会有很多有趣的性质。
trie 图
朴素 AC 自动机构建 fail 指针的复杂度是 \(O(n ^ 2)\) 的。trie 图用来优化 AC 自动机 fail 指针的构建过程。
具体地,对于一个节点 fa 来说,如果他的儿子 x 在 trie 树中存在,那么就把他的 fail 指针设成他父亲 fail 的对应儿子。即 tr[fa] -> son[x] -> fail = tr[fa] -> fail -> son[x]。如果它的儿子不存在,那么就把这个孩子设成父亲 fail 指针的对应儿子,也就是 tr[fa] -> son[x] = tr[fa] -> fail -> son[x]。这样的复杂度是 \(O(n)\) 的。
void trie_graph() { // 建 trie 图
queue<int> q;
for (int i = 0; i < 26; i ++ )
if (tr[0].s[i]) q.push(tr[0].s[i]);
while (q.size()) {
auto t = q.front(); q.pop();
for (int i = 0; i < 26; i ++ ) {
int v = tr[t].s[i];
if (!v) tr[t].s[i] = tr[tr[t].fail].s[i];
else {
tr[v].fail = tr[tr[t].fail].s[i];
q.push(v);
}
}
}
}
使用 trie 图 构建了无用节点的 fail 指针。用的时候只需要把有用的 fail 指针抽出来就是 fail 树了。
后缀数组 SA
原名应该是 \(\text{suffix-array}\)。
首先四个定义:
-
\(rk[i]\) 表示以 \(i\) 为开头的后缀在所有后缀中排名为 \(rk[i]\)。
-
\(sa[i]\) 表示排名为 \(i\) 的后缀的开头在原串中的 \(i\) 位置。\(sa\) 和 \(rk\) 互为逆运算。
-
\(hs[i]\) 表示以 \(i\) 开头的后缀与以排名比 \(i\) 小一的位置开头的后缀的最长公共前缀。即 \(\mathbf{LCP}(s[sa[rk[i] - 1] \cdots n], s[i \cdots n])\)。
-
\(hr[i]\) 表示排名为 \(i\) 的后缀与排名为 \(i - 1\) 的后缀的最长公共前缀。
下面通过倍增求 \(rk[], sa[]\) 两个数组。
首先将所有后缀按照其首字母进行排序可以得到 \(rk\) 数组。然后把 \(rk\) 累加到桶里做前缀和,从前往后 / 从后往前跑一边即可求出 \(sa\)。
for (int i = 1; i <= ls; i ++ ) bin[rk[i] = s[i]] ++ ;
for (int i = 1; i <= sz; i ++ ) bin[i] += bin[i - 1];
for (int i = ls; i >= 1; i -- ) sa[bin[rk[i]] -- ] = i;
接下来倍增。设当前有了后缀长度为 \(j\) 的 \(rk, sa\),要求长度为 \(2j\) 的 \(rk, sa\)。可以将长度 \(2j\) 的每个后缀看做长度为 \(j\) 的两个后缀拼起来。那么以第一个后缀为第一关键字,第二个后缀为第二关键字排序就可以得到新的 \(sa\)。这个算法实现非常简便,但是复杂度明显是 \(\Theta(n \log ^ 2 n)\) 的。
接下来考虑继续利用桶排。首先利用第二关键字排个序,把对应的第一关键字的位置存在 \(tp\) 数组里。然后按照刚开始以第一个字符为基准的求法桶排,就可以求出来新的 \(sa\) 数组。
for (int i = ls - j + 1; i <= ls; i ++ ) tp[ ++ tt] = i; // 最后 j 个的第一关键字最小。
for (int i = 1; i <= ls; i ++ )
if (sa[i] > j) tp[ ++ tt] = sa[i] - j; // 接下来按照第二关键字从小到大枚举。
for (int i = 1; i <= sz; i ++ ) bin[i] = 0;
for (int i = 1; i <= ls; i ++ ) bin[rk[i]] ++ ;
for (int i = 1; i <= sz; i ++ ) bin[i] += bin[i - 1];
for (int i = ls; i >= 1; i -- ) sa[bin[rk[tp[i]]] -- ] = tp[i];
然后考虑如何用新的 \(sa\) 数组求出新的 \(rk\) 数组。显然可以根据 \(rk[sa[i]] = i\) 这个性质。但是我们希望相同串排序相同。那不是很简单吗?如果两个位置第一关键字和第二关键字的 \(rk\) 都一样,辣么这两个后缀就一样力,然后就把原来的这两个位置的 \(rk\) 拍扁成一个就好啦。
然后跑完了。
swap(rk, tp); tt = rk[sa[1]] = 1; // rk 数组还有用,所以和 tp 交换一下。也可以 memcpy
rep(i, 2, ls) {
int x = (tp[sa[i]] != tp[sa[i - 1]]); // 如果不是一二关键字都相同就为 1,否则为 0
x |= (tp[sa[i] + j] != tp[sa[i - 1] + j]);
rk[sa[i]] = rk[sa[i - 1]] + x;
}
接下来考虑如何求 \(hs, hr\)。首先有性质 \(hs[i] \ge hs[i - 1] - 1\)。先这样更新着,然后从当前 \(hs\) 所在位置和 \(i\) 对应位置( \(i\) 排名减一所在位置)暴力判断判断,相等就加,直到不等。
然后跑完了。可以证明,上面的暴力算法复杂度是线性的。
rep(i, 1, ls) { // 求出 hs,hr 数组
hs[i] = max(hs[i - 1] - 1, 0);
while (s[i + hs[i]] == s[sa[rk[i] - 1] + hs[i]]) hs[i] ++ ;
hr[rk[i]] = hs[i];
}
总代码如下(输出了 \(sa\) 和 \(hr\)):
#include <iostream>
#include <cstring>
#include <cstdio>
#define rep(i, a, b) for (int i = (a); i <= (b); i ++ )
#define per(i, a, b) for (int i = (a); i >= (b); i -- )
using namespace std;
const int N = 1000010;
int sa[N], rk[N], sz;
int ls, tt, tp[N], bin[N];
int hs[N], hr[N];
char s[N];
int main() {
scanf("%s", s + 1);
ls = strlen(s + 1);
sz = max(ls, 255); // 255 为字符集大小
// 求出以第一位为基准的排序。
rep(i, 1, ls) bin[rk[i] = s[i]] ++ ;
rep(i, 1, sz) bin[i] += bin[i - 1];
per(i, ls, 1) sa[bin[rk[i]] -- ] = i;
// 求出以第 2j 位为基准的排序。
// 以前 j 位为第一关键字,[j, 2j] 位为第二关键字。
for (int j = 1; j <= ls; tt = 0, j <<= 1) {
rep(i, ls - j + 1, ls) tp[ ++ tt] = i; // 这个第二关键字就小,因为有空字符。
rep(i, 1, ls) if (sa[i] > j) tp[ ++ tt] = sa[i] - j; // 按照 sa 排序来看。
rep(i, 1, sz) bin[i] = 0; // 和上面一样,就是基排。
rep(i, 1, ls) bin[rk[i]] ++ ;
rep(i, 1, sz) bin[i] += bin[i - 1];
per(i, ls, 1) sa[bin[rk[tp[i]]] -- ] = tp[i];
swap(rk, tp); tt = rk[sa[1]] = 1; // rk 数组还有用,所以和 tp 交换一下。也可以 memcpy
rep(i, 2, ls) {
int x = (tp[sa[i]] != tp[sa[i - 1]]); // 如果不是一二关键字都相同就为 1,否则为 0
x |= (tp[sa[i] + j] != tp[sa[i - 1] + j]);
rk[sa[i]] = rk[sa[i - 1]] + x;
}
if (rk[sa[ls]] == ls) break; // 所有后缀都不相同,说明排完了。
}
rep(i, 1, ls) { // 求出 hs,hr 数组
hs[i] = max(hs[i - 1] - 1, 0);
while (s[i + hs[i]] == s[sa[rk[i] - 1] + hs[i]]) hs[i] ++ ;
hr[rk[i]] = hs[i];
}
rep(i, 1, ls) printf("%d ", sa[i]); puts("");
rep(i, 1, ls) printf("%d ", hr[i]);
return 0;
}
后缀数组应用的核心是 \(hs[], hr[]\) 两个数组,最主要的是 \(hr[]\)。有这样一个性质:
排名相邻的两个后缀的 \(\mathbf{LCP}\) 具有极大性。
这个性质非常有用。另外一个 \(\text{trick}\):子串集就是后缀的前缀集。
接下来是几道例题 / 典题:
例题1
\(\texttt{P4051 [JSOI2007] 字符加密}\)
求一个字符串置换的排序。
字符串的置换:如 \(\texttt{abcd}\) 的置换就为 \(\texttt{abcd, bcda, cdab, dabc}\)。
很显然的,将原串复制一份接到原来的后面,然后跑 \(\text{SA}\)。\(sa\) 数组中 \(\le n\) 的保持原偏序就是答案。
例题2
给定 \(n\) 个字符串,求出其两两最长公共子串。
\(n \le 50, \sum |s| \le 10 ^ 6\)。
首先考虑两个字符串应该怎么做。设两个字符串为 \(s1, s2\),将他们两个拼起来,中间加个分隔符。然后跑后缀数组。考虑将每个后缀 \(i, j\) 染色为 \(1\) 或 \(2\),表示其为 \(s_1\) 或 \(s_2\) 的后缀。接下来,由于 \(\mathrm{LCP}\) 的极大性,贪心地,我们需要让两个不同颜色的后缀靠的尽可能近。开个辅助数组记一下距离它最近的不同色后缀在哪里(当然是记他们中间的最小 \(\mathrm{LCP}\)),然后更新答案就好了。
多个字符串思路类似。全都接起来跑 \(\mathrm{SA}\),然后按照上述方法,记录距离每个点最近的不同色的最近后缀即可。
时间复杂度 \(\mathcal{O(|S| \log |S| + n |S|)}\)。
例题3
\(\texttt{P5546 [POI2000] 公共串}\)
求 \(n\) 个字符串的最长公共子串。
看起来很简单捏。
把 \(n\) 个串加个分隔符拼起来,然后跑 \(\text{SA}\)。然后考虑将每个后缀染色,染色为 \(i\) 表示开头字符在第 \(i\) 个字符串中。
然后转化成了这样的问题:找到公共 \(\mathrm{LCP}\) 最长的包含所有颜色的段。这个过程可以二分实现,同时也可以用双指针和单调队列。因为这个段需要尽量短,所以固定左指针,需要向右指针向右移动至恰好满足条件。然后根据 \(hr\) 维护单调递增队列即可。
例题4
求字符串 \(S\) 中不同子串个数
考虑利用容斥的思想。对 \(S\) 串跑 \(\text{SA}\) 之后,答案即为每个后缀的长度减去其 \(hs\) 之和。也就是所有子串的个数 \(C_n^2\) 减去本质相同的所有子串。
另外,此题也可以使用后缀自动机 \(\text{SAM}\) 来求解。这里不加赘述。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号