高级数据结构笔记
在本文中，你可能找到：线段树，可持久化数据结构（主席树等），李超树，K-D Tree，树套树，莫队等算法。
I 树套树
顾名思义，就是一个树套一个树。。。
广义的树套树是指嵌套多层的数据结构。常见的有：线段树套线段树（二维线段树），线段树套平衡树（“二逼平衡树”），分块套平衡树，树状数组套线段树（带修主席树）等等。
在这里，由于 set，map 等 STL 内部实现是平衡树，因此将这些 STL 的嵌套也算作树套树。
I.I 树套树解决偏序问题
树套树最典型的应用就是解决各种各样的偏序问题。
I.I.I P3810 【模板】三维偏序（陌上花开）
经典解法是 CDQ 分治。这里使用树状数组套权值线段树解决。
首先第一维是经典的排序，第二维可以使用树状数组维护起来。树状数组的每个节点维护一棵动态开点线段树，维护这个节点范围内所有节点的第三维信息。
时间复杂度 \(O(n \log ^ 2 n)\)，空间 \(O(n \log n)\)。
放一下主体部分代码：
struct node {
int ls, rs, s;
}tr[M];
#define lc tr[u].ls
#define rc tr[u].rs
#define mid (l + r >> 1)
void add(int &u, int l, int r, int x) {
if (!u) u = ++ cnt; tr[u].s ++ ;
if (l == r) return;
if (x <= mid) add(lc, l, mid, x);
else add(rc, mid + 1, r, x);
}
void ADD(int x, int y) {
for (int i = x; i <= m; i += (i & -i)) add(rt[i], 1, m, y);
}
int sum(int &u, int l, int r, int x) {
if (!u or l > x) return 0;
if (r <= x) return tr[u].s;
return sum(lc, l, mid, x) + sum(rc, mid + 1, r, x);
}
int SUM(int x, int y, int s = 0) {
for (int i = x; i; i -= (i & -i)) s += sum(rt[i], 1, m, y); return s;
}
I.I.II P3157 [CQOI2011] 动态逆序对
将删点操作倒过来，就是逆序加点的过程。
将加点的顺序（即时间轴）看做第一维，将下标看做第二维，将权值看做第三维。
这就是典型的三维偏序问题。直接树套树带走。
I.II 树套树解决二维数点问题
这里的二维数点定义比较广泛，包括点个数的计数，以及满足某些性质的点集查询等。
通常，二维数点问题有以下几种做法：
-
将第一维分块，块内套
set等数据结构维护第二维。同时对于每个 \(x\) 坐标建立一个set，用于维护散块信息。 -
对第一维建线段树，线段树节点里面套
set/ 平衡树。 -
对第一维建树状数组，树状数组每个节点里套
set/ 平衡树。
对于第一种方法，直接对于整块 / 散块里的平衡树 lower_bound 即可。
对于第二种方法，定位到线段树上的 \(O(\log n)\) 个区间之后和第一种一样。
对于第三种方法，需要根据情况具体分析。有时需要维护树状数组后缀 \(\max\) 或者前缀 \(\max\)，有时需要维护点数等等。优势是常数小。
I.II.I CF19D Points
很好的一道题。但是由于题目丧心病狂的卡常，我至今没有用树状数组套 set 卡过去。
题目显然是二维数点，属于求满足某种条件的点集类型题目。条件是某个点右上方的最左下的点。
第一种思路是分块套 set。对于横纵坐标离散化之后，对于每个横坐标维护一个 set，记录横坐标为该值的所有纵坐标。同时对每个块维护一个类型为 pair 的 set，维护横坐标在该块内的所有点。
每次插入和查询复杂度都是 \(O(\log n)\)。查询复杂度需要查询 \(O(\sqrt n)\) 个整块，每个整块需要 \(O(\log n)\) 的复杂度。需要查询 \(O(\sqrt n)\) 个单点，单点复杂度 \(O(\log n)\)。因此总复杂度 \(O(m \sqrt n \log n)\)。轻松的跑过去了。
第二种思路是树状数组套 set。对于纵坐标用树状数组维护，内层套 set 维护横坐标。插入的时候只需要在右端点 \(< y\) 的节点的 set 内插点就可以了。对于查询操作，只需要在左端点 \(\ge y\) 的节点 set 内 lower_bound 即可。复杂度 \(O(m \log ^ 2 n)\)。
不知道为什么，常数和复杂度都小的树状数组套 set 没有卡过去/kk
树状数组套 set ：
set<PII> s[N]; vector<int> p;
int n, lim;
struct Q { int op, x, y; }q[N];
void add(int x, int y) {
for (int i = y; i; i -= (i & -i)) s[i].insert(mp(x, y));
}
void del(int x, int y) {
for (int i = y; i; i -= (i & -i)) s[i].erase(mp(x, y));
}
PII ask(int x, int y) {
PII ans = mp(INF, INF);
for (int i = y; i <= lim; i += (i & -i))
ans = min(ans, *s[i].lower_bound(mp(x, y)));
return ans;
}
int main() {
read(n);
rep(i, 1, n) {
char ch[7]; int x, y;
scanf("%s", ch); read(x, y);
if (*ch == 'a') q[i] = {0, x, y};
if (*ch == 'r') q[i] = {1, x, y};
if (*ch == 'f') q[i] = {2, ++ x, ++ y};
p.push_back(y);
} sort(all(p)); p.resize(unique(all(p)) - p.begin());
lim = p.size();
auto find = [](int x) -> int {
return lower_bound(all(p), x) - p.begin() + 1;
};
rep(i, 1, n) q[i].y = find(q[i].y);
rep(i, 1, lim) s[i].insert(mp(INF, INF));
rep(i, 1, n) {
if (q[i].op == 0) add(q[i].x, q[i].y);
if (q[i].op == 1) del(q[i].x, q[i].y);
if (q[i].op == 2) {
register PII ans = ask(q[i].x, q[i].y);
if (ans.first == INF) puts("-1");
else write(' ', ans.first, p[ans.second - 1]), pc('\n');
}
} return 0;
}
I.II.II Intersection of Permutations
比较套路的一道题。若有 \(b_x = a_y\)，那么记 \(t_x = y\)。
问题转化成了：
-
查询操作：查询在 \(l_b \sim r_b\) 中，有多少 \(t_i \in [l_a, r_a] \bigcup \mathbb{Z}\)。
-
修改操作：交换 \(t_x, t_y\)。
这是一个带修的二维数点，直接树状数组套权值线段树带走。
注意要写空间回收，要不然会 MLE。
struct node { int ls, rs, s; }tr[M];
#define ls tr[u].ls
#define rs tr[u].rs
#define mid (l + r >> 1)
int New() { return !top ? ++ cnt : stk[top -- ]; }
void add(int &u, int l, int r, int x, int v) {
if (l > x or r < x) return;
if (!u) u = New(); tr[u].s += v; if (l == r) return;
add(ls, l, mid, x, v), add(rs, mid + 1, r, x, v);
if (!tr[u].s) stk[ ++ top] = u, u = 0;
}
void ADD(int x, int p, int v) {
for (int i = x; i <= n; i += (i & -i)) add(rt[i], 1, n, p, v);
}
int ask(int u, int l, int r, int L, int R) {
if (!u or r < L or l > R) return 0;
if (l >= L and r <= R) return tr[u].s;
return ask(ls, l, mid, L, R) + ask(rs, mid + 1, r, L, R);
}
int ASK(int la, int ra, int lb, int rb, int s = 0) { lb -- ;
for (int i = rb; i; i -= (i & -i)) s += ask(rt[i], 1, n, la, ra);
for (int i = lb; i; i -= (i & -i)) s -= ask(rt[i], 1, n, la, ra); return s;
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, n) scanf("%d", &a[i]), bin[a[i]] = i;
rep(i, 1, n) scanf("%d", &b[i]);
rep(i, 1, n) t[i] = bin[b[i]], ADD(i, t[i], 1);
while (m -- ) {
int op, la, ra, lb, rb, x, y;
scanf("%d", &op);
if (op & 1) {
scanf("%d%d%d%d", &la, &ra, &lb, &rb);
printf("%d\n", ASK(la, ra, lb, rb));
} else {
scanf("%d%d", &x, &y);
ADD(x, t[x], -1); ADD(y, t[y], -1);
swap(t[x], t[y]); ADD(x, t[x], 1); ADD(y, t[y], 1);
}
} return 0;
}
I.II.III CF785E Anton and Permutation(动态逆序对)
不知道应该归为二位数点问题还是偏序问题了。暂且放到这里。
考虑交换两个值 \(a_x, a_y(x < y)\) 后的结果。假设有一个值 \(a_z\)：
-
若 \(z < x\) 或者 \(z > y\)：交换之后对逆序对没有影响。
-
若 \(x < z < y\)，\(a_z < \min(a_x, a_y)\) 或 \(a_z > \max(a_x, a_y)\)：交换之后对逆序对没有影响。
-
若 \(x < z < y\)，\(a_x < a_z < a_y\)：
-
若 \(a_x > a_y\)，则交换后减少两个逆序对。
-
若 \(a_x < a_y\)，则交换后增加两个逆序对。
-
综上所述，问题转化为查询下标在 \(x \sim y\)，权值在 \(a_x \sim a_y\) 中的数的个数。
将下标看成横轴，权值看做纵轴，是经典的二维数点问题。直接树状数组套权值线段树带走。
int New() { return !top ? ++ cnt : stk[top -- ]; }
void add(int &u, int l, int r, int x, int v) {
if (l > x or r < x) return;
if (!u) u = New(); tr[u].s += v; if (l == r) return;
add(ls, l, mid, x, v), add(rs, mid + 1, r, x, v);
if (!tr[u].s) stk[ ++ top] = u, u = 0;
}
void ADD(int x, int p, int v) {
for (int i = x; i <= n; i += (i & -i)) add(rt[i], 1, n, p, v);
}
int ask(int u, int l, int r, int L, int R) {
if (!u or l > R or r < L) return 0;
if (l >= L and r <= R) return tr[u].s;
return ask(ls, l, mid, L, R) + ask(rs, mid + 1, r, L, R);
}
int ASK(int l, int r, int lv, int rv, int s = 0) {
for (int i = r; i; i -= (i & -i)) s += ask(rt[i], 1, n, lv, rv);
for (int i = l; i; i -= (i & -i)) s -= ask(rt[i], 1, n, lv, rv);
return s;
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, n) ADD(i, a[i] = i, 1);
while (m -- ) {
int x, y; scanf("%d%d", &x, &y);
if (x == y) { printf("%lld\n", last); continue; }
if (x > y) swap(x, y); bool f = (a[x] > a[y]);
ADD(x, a[x], -1), ADD(y, a[y], -1); swap(a[x], a[y]);
ADD(x, a[x], 1), ADD(y, a[y], 1);
if (f) last = last - 2ll * ASK(x, y - 1, a[x], a[y]) - 1;
else last = last + 2ll * ASK(x, y - 1, a[y], a[x]) + 1;
printf("%lld\n", last);
} return 0;
}
Double exp：P1975 [国家集训队] 排队
I.III 树套树解决带修区间第 \(k\) 大问题
不带修的区间第 \(k\) 大，正经解法就是主席树。
那么如果带修了呢？
可以外层一个树状数组维护下标，内层一个权值线段树维护这个区间的权值。
这样相当于把一棵主席树拆成了许多个动态开点线段树。树状数组每个节点上存这个区间里面所有线段树的根。
修改时，每次修改树状数组的 \(\log\) 个节点，每修改一个节点需要一个老哥，所以就是 \(O(\log ^ 2 n)\)。
查询就是前缀和的容斥。前缀和要在树状数组上做，所以是两个 \(\log\)。
经典例题：
I.III.I P2617 Dynamic Rankings
放一下主体部分代码：
struct node {
int ls, rs, s;
}tr[M]; int rt[N];
vector<int> L, R;
int n, m, cnt, a[N];
#define lc tr[u].ls
#define rc tr[u].rs
#define mid (l + r >> 1)
void add(int &u, int l, int r, int x, int v) {
if (l > x or r < x) return;
if (!u) u = ++ cnt; tr[u].s += v;
if (l == r) return;
add(lc, l, mid, x, v); add(rc, mid + 1, r, x, v);
}
void ADD(int x, int v, int c) {
for (int i = x; i <= n; i += (i & -i))
add(rt[i], 0, V, v, c);
}
int ask(int l, int r, int k) {
if (l == r) return r; int s = 0;
for (auto &u : R) s += tr[lc].s;
for (auto &u : L) s -= tr[lc].s;
if (k <= s) {
for (auto &u : L) u = lc;
for (auto &u : R) u = lc;
return ask(l, mid, k);
}
for (auto &u : L) u = rc;
for (auto &u : R) u = rc;
return ask(mid + 1, r, k - s);
}
int ASK(int l, int r, int k) {
L.clear(); R.clear(); l -- ;
for (int i = r; i; i -= (i & -i)) R.pb(rt[i]);
for (int i = l; i; i -= (i & -i)) L.pb(rt[i]);
return ask(0, V, k);
}
I.IV 树套树解决动态二维问题
就是二维线段树。第一维维护 \(x\) 第二维维护 \(y\)。第二维需要动态开点。
不过二维线段树一般没有写的，正常的矩形求和外面可以直接套一个树状数组。
查询的时候，只需要求横坐标在 \(1 \sim x_2\) 内，纵坐标在 \(y_1 \sim y_2\) 内的和，再减去横坐标在 \(1 \sim x_1 - 1\)，纵坐标在 \(y_1 \sim y_2\) 内的就可以了。
本质上还是一个二维偏序问题。
I.IV.I P3755 [CQOI2017] 老C的任务
二维线段树模板题。不带修矩形求和。横纵坐标达到 \(10 ^ 5\) 级别。
这里只放核心代码，离散化应该没有人不会。
struct node {
int ls, rs; LL s;
}tr[M];
#define ls tr[u].ls
#define rs tr[u].rs
#define mid (l + r >> 1)
void add(int &u, int l, int r, int x, LL v) {
if (l > x or r < x) return;
if (!u) u = ++ cnt; tr[u].s += v; if (l == r) return;
add(ls, l, mid, x, v), add(rs, mid + 1, r, x, v);
}
void ADD(int x, int y, LL p) {
for (int i = x; i <= V; i += (i & -i)) add(rt[i], 1, V, y, p);
}
LL ask(int u, int l, int r, int L, int R) {
if (l > R or L > r) return 0ll;
if (l >= L and r <= R) return tr[u].s;
return ask(ls, l, mid, L, R) + ask(rs, mid + 1, r, L, R);
}
LL ASK(int l1, int r1, int l2, int r2, LL s = 0ll) {
for (int i = r1; i; i -= (i & -i)) s += ask(rt[i], 1, V, l2, r2);
for (int i = l1 - 1; i; i -= (i & -i)) s -= ask(rt[i], 1, V, l2, r2);
return s;
}
// main
rep(i, 1, n) ADD(x[i], y[i], P[i]);
rep(i, 1, m) printf("%lld\n", ASK(x1[i], x2[i], y1[i], y2[i]));
Summary： 在大部分时候，需要维护的信息具有左 / 右端点固定或者可差分性时，使用树状数组套数据结构是一个不错的选择。
当然，有时分块套数据结构可以获得意想不到的小常数。
II 主席树
也就是可持久化线段树，可以解决区间 \(k\) 小值等经典问题。
II.I 主席树解决区间 \(k\) 小值问题
II.I.I P3834 【模板】可持久化线段树 2
-
如果只求一次 \(k\) 小值：
nth_element完美解决。 -
如果是全局 \(k\) 小值：
sort完美解决。 -
如果是区间 \(k\) 小值：树套树完美解决。
-
如果要求 \(O(n \log n)\) 复杂度。。。
这里需要用到主席树。主席树的本质是 \(n\) 颗权值线段树（其实也相当于是一个树套树，是数组套权值线段树（如果你把数组也当做数据结构的话））。第 \(i\) 颗线段树存储前 \(a_1 \sim a_i\) 的信息总和。之后可能会把外层的数组成为第一维，内层的权值线段树称为第二维。
比如在求区间 \(k\) 小值，第 \(i\) 颗树可以作为一个桶，将前 \(i\) 个元素都扔到桶里。求答案的时候，只需要把第 \(r\) 颗树和第 \(l - 1\) 颗树（这里的树就是桶）的对应位置相减，然后线段树二分即可。
比如数组 a = [3, 1, 3, 4, 2]，访问 \([2, 4]\) 的第 \(3\) 小值。
第 \(4\) 颗树是这样子的：[1, 0, 2, 1]，表示 \(1\) 出现 \(1\) 次，\(2\) 出现 \(0\) 次，以此类推。
第 \(1\) 颗树是这样子的：[0, 0, 1, 0]。
二者对应位置相减得到：[1, 0, 1, 1]。这个对应位置相减的树不需要建出来，只需要线段树二分的时候做就可以了。
想法是很好的，但是不可能把这 \(n\) 线段树都建出来。因为全部都建出来，空间将会达到珂怕的 \(O(n V)\)。
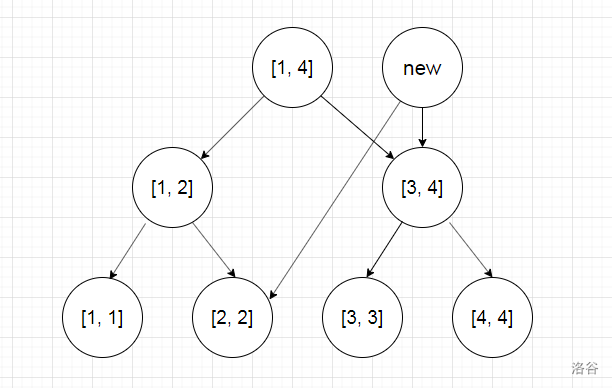
主席树使用了一个非常厉害的空间压缩方法：公用节点。
如果我们做的是单点修改，线段树每一层只会修改一个节点，一共只修改 \(\log n\) 个节点。也就是说，大部分节点和原来是完全一样的。
所以，每次修改只需要把变了的 \(\log n\) 个节点拎出来新建，剩下的节点原封不动复制过来就行了。这个复制过程也不需要进行，两个树可以共用同一个节点，所以直接把不变的旧节点挂到新树的对应位置就行了。
挂一张 OI-wiki 的图辅助理解。
红色的就是改动的点，黑色的都是不变的点，也是共用节点。
于是这道题完美解决。
需要注意的是，由于每次需要新建 \(\log V\) 个节点，因此空间复杂度应该是 \(n + m \log V\)。
const int N = 200010, V = 1e9;
int n, m, cnt, a[N], rt[N];
struct node {
int ls, rs, s;
}tr[N * 40];
#define lc tr[u].ls
#define rc tr[u].rs
#define mid (l + r >> 1)
void ins(int &u, int v, int l, int r, int x) {
if (l > x or r < x) return;
tr[u = ++ cnt] = tr[v], tr[u].s ++ ;
if (l == r) return; ins(lc, tr[v].ls, l, mid, x);
ins(rc, tr[v].rs, mid + 1, r, x);
}
int ask(int u, int v, int l, int r, int k) {
if (l == r) return r;
int s = tr[lc].s - tr[tr[v].ls].s;
if (s >= k) return ask(lc, tr[v].ls, l, mid, k);
else return ask(rc, tr[v].rs, mid + 1, r, k - s);
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, n) scanf("%d", &a[i]);
rep(i, 1, n) ins(rt[i], rt[i - 1], 0, V, a[i]);
while (m -- ) {
int l, r, k; scanf("%d%d%d", &l, &r, &k);
printf("%d\n", ask(rt[r], rt[l - 1], 0, V, k));
} return 0;
}
对于一般的写法，主席树需要先建树。不过我个人感觉没必要。
II.I.II P2633 Count on a tree（树上路径第 k 小）
非常简单题，只不过把主席树放到了树上。
这里的第二维和原来有所不同，表示的是从 \(i\) 号节点到根节点上的权值集合。
当然，共用节点肯定儿子共用了父亲的，也就是在父亲的基础上建儿子（序列上的主席树是在 \(i - 1\) 的基础上建新树。这是不同的地方）。
剩下的就是一个树上差分的事情了。复杂度 \(O(n \log n)\)。
马蜂有点毒瘤，凑付着看吧。
int n, m, cnt, w[N], rt[N];
int h[N], e[M], ne[M], idx;
int fa[N][21], dep[N], last;
struct node {
int ls, rs, s;
}tr[N * 20];
#define ls(u) tr[u].ls
#define rs(u) tr[u].rs
#define mid (l + r >> 1)
void add(int a, int b) {
e[ ++ idx] = b, ne[idx] = h[a], h[a] = idx; }
void ins(int &u, int v, int l, int r, int x) {
if (l > x or r < x) return;
tr[u = ++ cnt] = tr[v]; tr[u].s ++ ; if (l == r) return;
ins(ls(u), ls(v), l, mid, x); ins(rs(u), rs(v), mid + 1, r, x);
}
int ask(int u, int v, int w, int x, int l, int r, int k) {
if (l == r) return r;
int s = tr[ls(u)].s + tr[ls(v)].s - tr[ls(w)].s - tr[ls(x)].s;
if (s >= k) return ask(ls(u), ls(v), ls(w), ls(x), l, mid, k);
else return ask(rs(u), rs(v), rs(w), rs(x), mid + 1, r, k - s);
}
void dfs(int u, int f) {
ins(rt[u], rt[f], 1, p.size(), w[u]);
fa[u][0] = f; dep[u] = dep[f] + 1;
for (int i = h[u]; i; i = ne[i]) if (e[i] ^ f) dfs(e[i], u);
}
void init() {
rep(j, 1, 20) rep(i, 1, n) fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
int lca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
dep(i, 20, 0) if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
if (u == v) return u;
dep(i, 20, 0) if (fa[u][i] ^ fa[v][i]) u = fa[u][i], v = fa[v][i];
return fa[u][0];
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, n) scanf("%d", &w[i]);
rep(i, 1, n) p.push_back(w[i]);
sort(all(p)); p.resize(unique(all(p)) - p.begin());
rep(i, 1, n) w[i] = lower_bound(all(p), w[i]) - p.begin() + 1;
dfs(1, 0); init();
rep(i, 1, n - 1) {
int a, b; scanf("%d%d", &a, &b); add(a, b); add(b, a);
} dfs(1, 0); init();
while (m -- ) {
int u, v, k; scanf("%d%d%d", &u, &v, &k);
u = u ^ last; int l = lca(u, v);
int s = ask(rt[u], rt[v], rt[l], rt[fa[l][0]], 1, p.size(), k) - 1;
printf("%d\n", last = p[s]);
} return 0;
}
II.I.III Noble Knight's Path
还没写这个，感觉有点毒瘤，不过思路还是非常简单的。本质是上一道题的加强带修版。
首先肯定是树剖。套一个主席树。第一维维护时间，第二维维护权值（\(1\) 表示没有被亵渎，\(0\) 表示被亵渎了）。查询的时候直接线段树上二分就行了。
时间当然是 \(O(n \log ^ 2 n)\)。看起来有点大，但是树剖小常数还有 \(4.00\) 秒时限，优势在我。
II.II 主席树解决区间 mex 问题
II.II.I P4137 Rmq Problem / mex
主席树内层仍然是权值线段树，只不过维护的信息不同了。
先转化一下问题：对于 \([1, r]\) 这个区间里面，最后一次出现下标小于 \(l\) 的最大数。
这里需要维护的信息是：当前权值区间里面，最后一次出现下标最小的下标是多少。最后只需要在 \(r\) 这颗权值线段树里面二分即可。
当然，这是一个比较麻烦的做法。更好的做法是将操作离线下来之后，按照右端点排序，一颗线段树就可以解决问题。这样空间和时间都更优秀。
void ins(int &u, int v, int l, int r, int x, int c) {
if (l > x or r < x) return;
tr[u = ++ cnt] = tr[v]; if (l == r) return void(tr[u].mn = c);
ins(lc, tr[v].ls, l, mid, x, c), ins(rc, tr[v].rs, mid + 1, r, x, c);
tr[u].mn = min(tr[lc].mn, tr[rc].mn);
}
int ask(int u, int l, int r, int v) {
if (l == r) return r;
if (tr[lc].mn >= v) return ask(rc, mid + 1, r, v);
else return ask(lc, l, mid, v);
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, n) scanf("%d", &a[i]);
rep(i, 1, n) ins(rt[i], rt[i - 1], 1, V, a[i] + 1, i);
while (m -- ) {
int l, r; scanf("%d%d", &l, &r);
printf("%d\n", ask(rt[r], 1, V, l) - 1);
} return 0;
}
III 线段树进阶
建议有一定的线段树基础后食用。
会提到一些关于线段树的常见技巧。
III.I 线段树势能分析
往往与 \(\gcd, \varphi\) 与开根相关。
III.I.I hdu5828 Rikka with Sequence（区间加区间开根）
称线段树中 \(\max - \min > 1\) 的节点为关键点。
设 \(\Phi\) 为关键点个数，一次区间加会使得 \(\Phi\) 增加 \(O(\log n)\)，一次区间开根可以使 \(\Phi\) 增加 \(O(\log n)\)。但是一个区间开根 \(O(\log \log V)\) 次就不是关键点了。
因此 \(\Delta \Phi = O(m \log n)\)。每次对着非关键点打 tag，对着关键点暴力开根就可以了。
时间复杂度 \(O(n \log n \log \log V)\)。
上文中的 \(\Phi\) 就是势能。
III.I.II CF438D The Child and Sequence
仍然设关键点的个数为势能 \(\Phi\)。每次取模后一个数要么不变，要么减半。当且仅当模数大于被模数时不变。
\(\Phi\) 的变化和上面一道题相同，不同的是一个数被取模 \(O(\log V)\) 次会不变。
所以 \(\Delta \Phi = O(m \log n)\)。每次修改的时候，如果当前区间的 \(\max\) 比模数小则跳过，否则暴力递归。时间 \(O(m \log n \log V)\)。
III.I.III Another possible problem HDU Rikka with Phi
分析过程和上面类似，就不说了。
III.II 线段树优化建图
有的时候会遇到一个节点向编号连续的一堆点连边，或者一堆编号连续的点连边一个点。点数多的时候复杂度会爆到 \(O(n ^ 2)\)。
于是有了线段树优化建图。
线段树优化建图分为两颗树，一颗叫出树，另一颗叫入树。出树边由父亲指向儿子，入树由儿子指向父亲。
下面是一颗出树。
假设需要将一个点与编号在 \([2, 4]\) 里的所有点连边。首先先定位出两个区间 \([2, 2], [3, 4]\)。然后将新点连到这两个节点上去。然后就做完了。。。
每次只会定位出来 \(O(\log n)\) 个区间，所以每次只需要连 \(O(\log n)\) 条边。复杂度当然就是 \(O(m \log n)\)。
出树同理，可以解决编号在 \([l, r]\) 里所有点向某个点连边的问题。
平时我大多写 ST 表优化建图（感觉更简单，常数也更小），没有写过线段树优化建图。但是例题还是照例放一下：
III.II.I CF786B Legacy
这个是板子题。给一个 ST 表优化建图的代码，线段树优化建图可以类比参悟一下。
read(n, q, s);
rep(i, 1, n) st[i][0][0] = st[i][0][1] = ++ cnt;
rep(j, 1, 20) rep(i, 1, n) {
if (i + (1 << j) - 1 > n) break;
st[i][j][0] = ++ cnt; add(st[i][j - 1][0], cnt, 0);
add(st[i + (1 << (j - 1))][j - 1][0], cnt, 0);
st[i][j][1] = ++ cnt; add(cnt, st[i][j - 1][1], 0);
add(cnt, st[i + (1 << (j - 1))][j - 1][1], 0);
} while (q -- ) {
int op, u, v, l, r, w; read(op);
if (op == 1) read(v, u, w), add(v, u, w);
else {
read(v, l, r, w);
int k = log2(r - l + 1);
if (op & 1)
add(st[l][k][0], v, w), add(st[r - (1 << k) + 1][k][0], v, w);
else
add(v, st[l][k][1], w), add(v, st[r - (1 << k) + 1][k][1], w);
}
}
fill(d + 1, d + cnt + 1, INF);
priority_queue<PLL, vector<PLL>, greater<PLL>> q;
q.push({0, s}); d[s] = 0;
while (q.size()) {
auto u = q.top().second; q.pop();
if (vis[u]) continue; vis[u] = true;
for (int i = h[u]; i; i = ne[i]) {
int v = e[i]; if (d[v] > d[u] + w[i])
d[v] = d[u] + w[i], q.push({d[v], v});
}
} for (int i = 1; i <= n; i ++ )
printf("%lld ", d[i] == INF ? -1 : d[i]);
IV. k-D Tree(KDT , k-Dimension Tree)
KDT 是一种特殊的二叉搜索树，可以高效处理 \(k\) 维空间信息。
其相对于 CDQ 分治的优点是可以高度模板化，而不需要额外写函数；另外还可以带修。
在算法竞赛中，一般 \(k = 2\)。下文中如果无特殊说明，\(k = 2\)。
首先假设平面上有这么一堆点：
我要维护这一堆点。
首先有一个简单的想法：找到一个点，以这个点为分界点，在它左边（横坐标比他小）的分到他的左子树，剩下的分到右子树。左右递归处理。
但是这样做是不对的。比如在上图中我选点，依次选 \(F, E, B, D, C, A\)，树高直接干到 \(O(n)\)。这是非常不好的，因为这意味着我查询的时候可能要遍历所有点。
所以想到了另外的一种方法：每次按照横坐标排序，找到横坐标中位数所对应的点。把这个点当做划分点。这样左右两边的点数就相等了（？）。
乍一看，这样每次都能减少一半的点，树高就是 \(\log n + O(1)\) 了。但是其实不然。比如你想这样一种情况：假设所有点的横坐标都相等，那么每次有 \(n - 1\) 个点被划分到左边。所以还是会被卡成一条链。
因此需要更牛逼的优化：交替建树。
交替建树的思想是这样的：首先按照 \(x\) 坐标排序，选择中位数作为划分点。与刚才做法不一样的是，他的左右儿子应该选择按照 \(y\) 坐标排序，选择中位数作为划分点。接下来再按照 \(x\)，再按照 \(y\)，以此类推。由于排序键值交替变化，所以叫做交替建树。
可以发现，这样做，构建出的 K-D Tree 高度就是 \(\log n + O(1)\) 了。
比如刚才那个图中，建树过程是这样的：
建出的树形态是这样的：
于是，KDT 就以划分的方式，维护了平面上的 \(n\) 个点。
有人说 KDT 像线段树，但我觉得更像平衡树。因为线段树的非叶节点是不存储信息的，而 KDT 存储信息。另外，KDT 也具有可二分性。对于一个点 \(k\)，假设其划分依据为 \(z(z = 1, 2)\) 维，那么其左边的 \(z\) 维小于它，右面的大于它。这也与 BST 更为相似。
KDT 建完了，那么该如何进行操作呢？
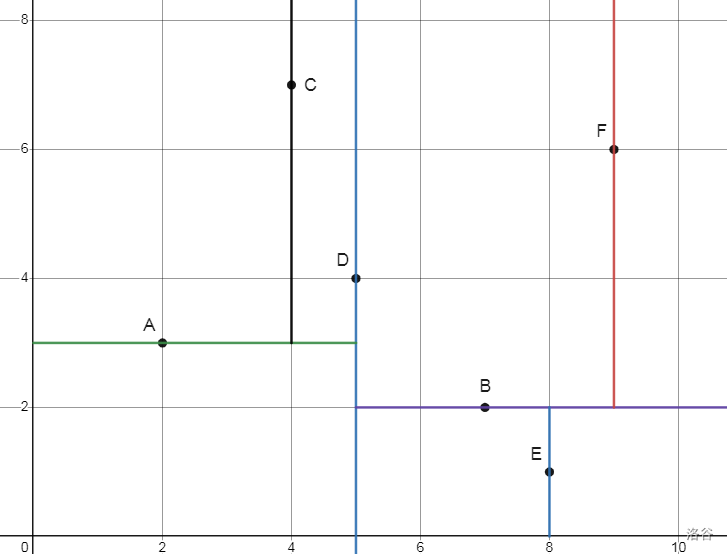
说起来非常玄学，KDT 进行操作的方法就像是暴力剪枝。对于一个点来说，对于每个维度 \(z(z \in \mathbb{Z}, z \le k)\)，需要维护这个维度意义下最靠左的点和最靠右的点。这样相当于把整个平面划分成了若干个矩形。
如果当前子树对应的矩形与所求矩形没有交点，则不继续搜索其子树；如果当前子树对应的矩形完全包含在所求矩形内，返回当前子树内所有点的权值和；否则，判断当前点是否在所求矩形内，更新答案并递归在左右子树中查找答案（这段话来自 OI-wiki，因为写的太好了就直接摘过来了）。
时间复杂度我不会证明啊，有兴趣看 OI-wiki 吧。最后结论是 \(T(n) = O(n ^ {1 - \frac{1}{k}})\)。
下面开始肝题。
IV.I. KDT 解决最近 / 最远点对问题
IV.I.I. P1429 平面最近点对（加强版）
求平面上 \(n\) 个点钟最近点对之间的距离（距离为欧氏距离）。
这是 KDT 的板子题。
首先按照刚才说的建树方法建树。询问的时候，从 \(1\) 到 \(n\)，每次钦定 \(i\) 号点作为点对中的一个，只需要找到距离这个点最近的点就可以了。
定义 \(m_l\) 表示左子树里面到 \(i\) 号点最近可能是多少。注意这里是可能。右子树同理。
如果 \(m_l\) 大于当前的答案，说明左子树无论怎么搞都不可能有成为答案的希望了。那么直接 ban 掉。\(m_r\) 同理。
如果 \(m_l < m_r\)，那么优先递归左子树（毕竟希望更大一些）。否则递归右子树。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define rop(i, a, b) for (int i = (a); i < (b); i ++ )
using namespace std;
const int N = 200010;
int cur, K, n;
double ans;
struct node {
int ls, rs;
double d[2], mn[2], mx[2];
// d[i] 表示第 i 维度的坐标值。
// mx[i] 表示第 i 维度最大的值。
// mx[i] 表示第 i 维度最小的值。
bool operator < (const node &t)const { // 按照第 K 维进行排序
return d[K] < t.d[K];
}
}tr[N];
#define ls tr[u].ls
#define rs tr[u].rs
void chkmin(double &a, double b) { a = min(a, b); }
void chkmax(double &a, double b) { a = max(a, b); }
void pushup(int u) {
rop(i, 0, 2) {
tr[u].mn[i] = tr[u].mx[i] = tr[u].d[i];
if (ls) chkmin(tr[u].mn[i], tr[ls].mn[i]), chkmax(tr[u].mx[i], tr[ls].mx[i]);
if (rs) chkmin(tr[u].mn[i], tr[rs].mn[i]), chkmax(tr[u].mx[i], tr[rs].mx[i]);
}
}
int build(int l, int r, int k) {
if (l > r) return 0;
int u = l + r >> 1;
K = k; nth_element(tr + l, tr + u, tr + r + 1); // 求出中位数并划分
ls = build(l, u - 1, k ^ 1); rs = build(u + 1, r, k ^ 1); // k ^ 1 交替建树
pushup(u); return u;
}
double sq(double x) { return x * x; }
double dist(int u, double s = 0.00) {
for (int i = 0; i < 2; i ++ )
s += sq(tr[cur].d[i] - tr[u].d[i]);
return s;
}
double mndis(int u, double s = 0.00) { // 最小的可能距离
rop(i, 0, 2) s += sq(max(tr[cur].d[i] - tr[u].mx[i], 0.0));
rop(i, 0, 2) s += sq(max(tr[u].mn[i] - tr[cur].d[i], 0.0));
return s;
}
void ask(int u) {
if (!u) return; if (u != cur) chkmin(ans, dist(u));
double dl = mndis(ls), dr = mndis(rs);
if (dl < dr) { if (dl < ans) ask(ls); if (dr < ans) ask(rs); }
if (dr < dl) { if (dr < ans) ask(rs); if (dl < ans) ask(ls); }
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
scanf("%lf%lf", &tr[i].d[0], &tr[i].d[1]);
int root = build(1, n, 0); ans = 2e18;
for (int i = 1; i <= n; i ++ ) cur = i, ask(root);
printf("%.4lf\n", (double)sqrt(ans));
return 0;
}
