多项式(Poly)笔记
开头先扔板子:多项式板子们
定义
多项式(polynomial)是形如 的代数表达式。其中 是一个不定元。
称为这个多项式的次数。
多项式的基本运算
- 多项式的加减法
- 多项式的乘法
- 多项式除法
这里讨论多项式的带余除法。
可以证明,一定存在唯一的 满足 ,且 。
称为 除 的商式, 称为 除 的余式。记作:
特别的,若 ,则称 整除 , 是 的一个倍式, 是 的一个因式。记作 。
有关多项式的引理
-
对于 个点可以唯一确定一个 次多项式。
-
如果 都是不超过 次的多项式,且它对于 个不同的数 有相同的值,即 。则 。
多项式的点值表示
如果选取 个不同的数 对多项式进行求值,得到 ,那么就称 为 的点值表示。
快速傅里叶变换(FFT)
快速傅里叶变换是借助单位根进行求值和插值,从而快速进行多项式乘法的算法。
单位根
将复平面上的单位圆均分成 份,从 轴数,第 条线与单位圆的交点称为 次单位根,记作 。
根据定义,可以得到:。
根据欧拉恒等式,可以得到:。
由此那么可以得到下面的性质:
离散傅里叶变换(DFT)
离散傅里叶变换,是将 代入 和 中求值的过程。
对于朴素的方法,每次代入一个单位根,然后用 的复杂度计算函数值。时间复杂度 。
离散傅里叶变换利用了单位根的性质巧妙优化了这个过程。离散傅里叶变换过程如下:
首先将 根据次数的奇偶性拆成两部分,分别分为:
设
则 。
将 代入得到:
然后你发现, 和 仅仅差了一个符号!!!
所以只需要求出 和 对 ()上的取值,就可以推出 在两倍点数上的取值。
每次问题规模缩小一半,因此时间复杂度 。
离散傅里叶逆变换(IDFT)
假设对于两个多项式都得到了 个点值,设为 。
那么可以知道,多项式 的点值表示一定为:
现在,只需要将这 个点插值回去,就可以得到 了。
先设这 个点值分别是:,设最后的多项式为 ,这里直接给出结论:
由此可见,IDFT 和 DFT 仅仅有一个负号的区别。只要将所有的单位根从 变成 即可。
void FFT(cp a[], int n, int op) {
if (n == 1) return;
cp a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
cp Wk = {1, 0};
rop(i, 0, n >> 1) {
a[i] = a1[i] + Wk * a2[i];
a[i + (n >> 1)] = a1[i] - Wk * a2[i];
Wk = Wk * Wn;
}
}
void FFT(cp a[], cp b[], int n, int m) {
m = n + m; n = 1;
while (n <= m) n <<= 1;
FFT(a, n, 1); FFT(b, n, 1);
rop(i, 0, n) a[i] = a[i] * b[i];
FFT(a, n, -1);
rep(i, 0, m) a[i].x = a[i].x / n;
}
FFT 优化
- 三次变两次优化
原本的朴素 FFT,将 两个序列分别求值,乘起来再 IDFT 插值一下,一共跑了三次 FFT。这是不好的。
三次变两次优化是这样的:将原序列合并成一个复数:。做一遍 DFT 把求出的每个函数值平方。因为 。因此把虚部取出来以后除以 就是答案。
void FFT(cp a[], int n, int op) {
if (n == 1) return;
cp a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
cp Wk = {1, 0};
rop(i, 0, n >> 1) {
a[i] = a1[i] + a2[i] * Wk;
a[i + (n >> 1)] = a1[i] - a2[i] * Wk;
Wk = Wk * Wn;
}
}
int main() {
read(n, m);
rep(i, 0, n) scanf("%lf", &a[i].x);
rep(i, 0, m) scanf("%lf", &a[i].y);
m = n + m; n = 1;
while (n <= m) n <<= 1;
FFT(a, n, 1);
rop(i, 0, n) a[i] = a[i] * a[i];
FFT(a, n, -1);
rep(i, 0, m) printf("%d ", (int)(a[i].y / 2 / n + 0.5));
}
- 蝴蝶变换优化
后面再补吧。其实本人感觉这个优化不是那么必要,因为三次变两次实在太快了。
FFT 例题
可以设 ,把 写成 的形式()。同理可以把 转化为多项式 。
这样求两个数相乘就是求 啊。
所以直接 做完了。
给出 个数 ,定义
对 ,求 的值。
首先发现这个除以 就是没用。所以可以化简成:
先看前面这个式子。答案就是:
设 。可以发现,
再看后面这一块的式子。我们把 的系数翻转,变成 。那么可以发现 。
跑两次 FFT 就完事了。
首先发现加减相对于两个手环是对称的。因此可以把对一个手环的减法转化成对另一个手环的加法。这样可以假设全是在第一个手环上执行的加减操作。
第一个手环执行了加 的操作,且旋转过之后的序列为 ,第二个手环为 。计算差异值并化简,可以得到差异值是:
可以发现,这个序列只有最后一项是不定的。
因此将 序列翻转后再复制一倍,与 卷积,答案就是卷积后序列的 项系数的 。
直接暴力枚举 ,加上前面依托就行了。
快速数论变换(NTT)
快速数论变换就是基于原根的快速傅里叶变换。
首先考虑快速傅里叶变换用到了单位根的什么性质。
-
互不相同。
-
。
-
。
数论中,原根恰好满足这些性质。
对于一个素数的原根 ,设 。那么:
我们发现它满足 的全部性质!
因此,只需要用 带替全部的 就可以了。
tips:对于一个质数,只有当它可以表示成 ,且需要满足多项式的项数 时才能使用 NTT。 后面有个加一,是因为 指数的分子上出现了 ; 需要时二的整数次幂,是因为每次都要除以 。
bonus:常用质数及原根
void NTT(int *a, int n, int op) {
if (n == 1) return;
int a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
NTT(a1, n >> 1, op), NTT(a2, n >> 1, op);
int gn = qpow((op == 1 ? g : invg), (mod - 1) / n), gk = 1;
rop(i, 0, n >> 1) {
a[i] = (a1[i] + 1ll * gk * a2[i]) % mod;
a[i + (n >> 1)] = (a1[i] - 1ll * gk * a2[i] % mod + mod) % mod;
gk = 1ll * gk * gn % mod;
}
}
NTT 优化:蝴蝶变换
盗大佬一张图
这是进行 NTT 的过程中数组下标的变化。
这样看似乎毫无规律。但是把他们写成二进制:
变换前:
变换后:
可以发现,就是对每个下标进行了二进制翻转。
因此可以先预处理出每个下标在递归底层对应的新下标。然后从底层往顶层迭代合并。
预处理每个下标的二进制翻转:
rop(i, 0, n) rev[i] = rev[i >> 1] >> 1 | (i & 1) << bit;
优化后的 NTT:
void NTT(int *a, int n, int op) {
rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
int gn = qpow((op == 1 ? g : invg), (mod - 1) / (mid << 1));
for (int i = 0, gk = 1; i < n; i += (mid << 1), gk = 1)
for (int j = 0; j < mid; j ++ , gk = 1ll * gk * gn % mod) {
int x = a[i + j], y = 1ll * a[i + j + mid] * gk % mod;
a[i + j] = Mod(x + y), a[i + j + mid] = Mod(x - y);
}
}
}
当然了,FFT 也可以用蝴蝶变换来优化。实践证明,速度变快了至少二分之一。
FFT 的迭代实现
void FFT(cp *a, int n, int op) {
rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
cp Wn = {cos(pi / mid), op * sin(pi / mid)};
for (int i = 0; i < n; i += (mid << 1)) {
cp Wk = {1, 0};
for (int j = 0; j < mid; j ++ , Wk = Wk * Wn) {
cp x = a[i + j], y = Wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
任意模数多项式乘法(MTT)
计算 的结果( 不一定能够表示成 的形式)。
这个东西有两种做法,但是我只学会了三模 NTT。
首先,卷积之后每个系数最多达到 的大小。拿模板题举例,这个东西就是 。因此只需要找三个模数 ,满足 ,然后用他们分别 NTT,最后再 CRT / exCRT 合并即可。
int CRT(int a, int b, int c, int p) {
int k = 1ll * Mod(b - a, p2) * inv1 % p2;
LL x = 1ll * k * p1 + a;
k = 1ll * Mod((c - x) % p3, p3) * inv2 % p3;
x = (x + 1ll * k * p1 % p * p2 % p) % p;
return x;
}
void MTT(int *a, int n, int *b, int m, int p) {
int B = ((n + m) << 2) + 1;
rev = new int [B]();
int *a1 = new int [B](), *b1 = new int [B]();
int *a2 = new int [B](), *b2 = new int [B]();
int *a3 = new int [B](), *b3 = new int [B]();
rop(i, 0, B)
a1[i] = a2[i] = a3[i] = a[i], b1[i] = b2[i] = b3[i] = b[i];
NTT(a1, n, b1, m, p1); NTT(a2, n, b2, m, p2); NTT(a3, n, b3, m, p3);
inv1 = inv(p1, p2); inv2 = inv(1ll * p1 * p2 % p3, p3);
rep(i, 0, n + m) a[i] = CRT(a1[i], a2[i], a3[i], p);
}
这里选择的模数为:。他们的原根都为 。
多项式求逆
求多项式 的逆元 。 的逆元定义为满足 的多项式 。
使用倍增法即可求出多项式的逆元。
首先假设已经求出了 。再假设 意义下逆元为 。那么有:
两边同时乘以 ,可以得到:
倍增求即可。
void Inv(int *f, int *g, int n) {
if (n == 1) {
g[0] = inv(f[0]); return;
} Inv(f, g, (n + 1) >> 1);
int m = 1, bit = 0;
while (m < (n << 1)) m <<= 1, bit ++ ; bit -- ;
rop(i, 0, n) tmp[i] = f[i];
rop(i, n, m) tmp[i] = 0;
rev = new int [m + 5]();
rop(i, 1, m) rev[i] = (rev[i >> 1] >> 1) | (i & 1) << bit;
NTT(tmp, m, 1); NTT(g, m, 1);
rop(i, 0, m) g[i] = (2ll - 1ll * g[i] * tmp[i] % p + p) % p * g[i] % p;
NTT(g, m, -1); int invn = inv(m);
rop(i, 0, m) g[i] = 1ll * g[i] * invn % p;
rop(i, n, m) g[i] = 0;
free(rev); rev = NULL;
}
分治 FFT
给定序列 ,求序列 。
其中 ,边界为 。
答案对 取模。
其实这是个多项式求逆板子
首先考虑生成函数 。然后可以发现:
因此 ,也就是:
所以直接设 ,然后把 求逆就行了。
read(n);
rop(i, 1, n) read(g[i]);
rop(i, 1, n) g[i] = Poly::p - g[i];
(g[0] += 1) %= Poly::p; Poly::Inv(g, n);
rop(i, 0, n) write(' ', g[i]); return 0;
多项式对数函数(Polyln)
给定 ,求多项式 使得
前置知识:简单的求导和积分,以及基本的多项式模板。
首先设 ,那么
然后对同余方程两边同时求导,得到
根据复合函数求导公式 可得,
然后又有 ,因此
计算 和 作为 。计算 得到 ,然后求 的积分就好了。
积分公式:。
void der(int *f, int n) { rep(i, 1, n) f[i - 1] = 1ll * i * f[i] % p; f[n] = 0; }
void Int(int *f, int n) {dep(i, n, 1) f[i] = 1ll * inv(i) * f[i - 1] % p; f[0] = 0; }
void Ln(int *f, int n) {
int B = (n << 2) + 5; int *_f = new int[B]();
rep(i, 0, n) _f[i] = f[i];
der(_f, n), Inv(f, n);
NTT(f, n, _f, n); Int(f, n);
free(_f); _f = NULL;
}
多项式指数函数(PolyExp)
给定多项式 ,求 满足 。
前置知识:牛顿迭代。
牛顿迭代是用来求函数零点的有力工具。
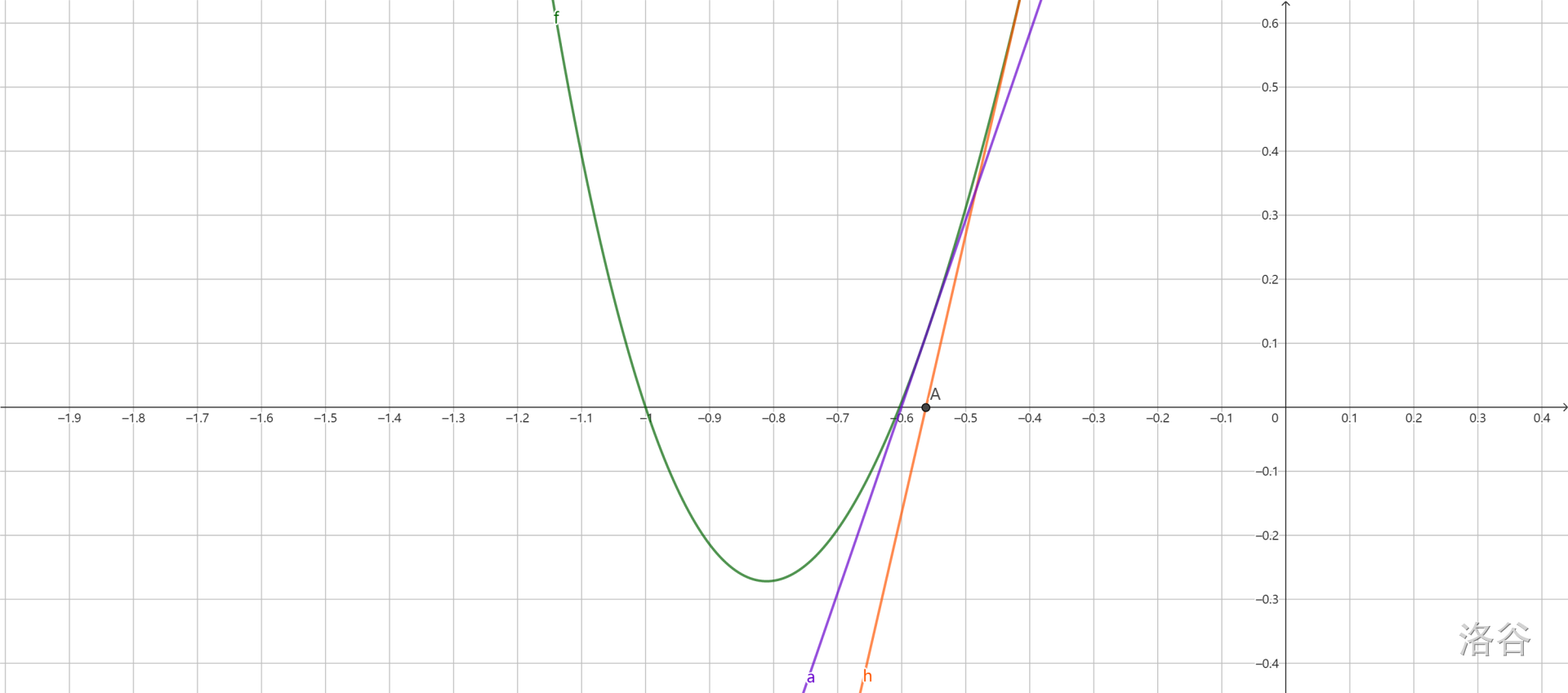
例如,下面这个图是使用牛顿迭代法求 零点的过程。
首先,随便选择一个点 ,过这个点做 的切线。切线方程是 。它与 轴交于一点 。
接下来,再令 ,过点 再做 的切线,与 轴交于点 。
再令 ,如此迭代下去。可以发现, 会逐渐逼近零点。
刚才说切线方程为 。如果令 ,得到的 便是切线方程与 轴的交点,为
运用于多项式,假设要求使 的多项式 ,并且已经知道 。
那么可以说,
接下来解决多项式 Exp。所求为 使得 。两边都取 得到:
移项得:
设 ,那么所求就是 的零点。
假设已经有 使得 ,根据上面的牛顿迭代,有:
根据这个柿子倍增求即可。每次需要计算一个 ,一个乘法,时间 。
写的有点丑,超级大肠数。
void Exp(int *f, int *g, int n) {
if (n == 1) return void(g[0] = 1);
Exp(f, g, (n + 1) >> 1);
int B = (n << 2) + 5; int *lnb = new int[B]();
rop(i, 0, n) lnb[i] = g[i]; Ln(lnb, n);
tmp = new int[B](); rop(i, 0, n) tmp[i] = f[i];
rop(i, 0, n) tmp[i] = (1ll * tmp[i] - lnb[i] + p) % p;
tmp[0] ++ ; NTT(g, n, tmp, n);
free(tmp); tmp = NULL; free(lnb); lnb = NULL;
}
多项式快速幂(PolyPower)
在模 意义下计算 。
有了前面的知识铺垫,这部分就非常的简单。
根据对数恒等式,有 。
因此 。
把 乘以 ,求多项式 ,然后再 exp 回来就行了。
void Power(int *f, int n, int k) {
Ln(f, n); rop(i, 0, n) f[i] = 1ll * f[i] * k % p; Exp(f, n);
}
多项式开根
在模 意义下计算 。
这个最简单。直接把 ,然后多项式快速幂。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【.NET】调用本地 Deepseek 模型
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库