浅谈泰勒展开

什么是导数

对于一个一次函数 \(\mathrm{f(x) = kx + b}\) 来说，我们发现 \(\mathrm{x}\) 每增加一个单位长度，\(\mathrm{f(x)}\) 都会相应的增加 \(\mathrm{k}\) 个单位长度。\(\mathrm{k}\) 就被称为一次函数 \(\mathrm{f(x) = kx + b}\) 的斜率。

同样的，我们想要推广到 \(\mathrm{f(x) = x^2}\) 上。但我们发现对于 \(\mathrm{x_0}\)，将它增加 \(\mathrm{\Delta x}\) 之后，\(\mathrm{f(x_0)}\) 增加的大小并不一定一样。因此我们发明了导数。

---

对于一个特定的 \(\mathrm{x}\)，我们将 \(\mathrm{x}\) 附近极小范围内的一段函数斜率记为函数 \(\mathrm{f(x)}\) 在 \(\mathrm{x}\) 的导数，记作 \(\mathrm{f(x)^{'}}\)。

将上面的文字数学化，即为：

\[\mathrm{f(x)^{'} = \lim_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x}} \]

花费一点时间，可以发现导数运算的一些规律：

• \({(f(x) + g(x)) ^ {'} = f(x)^{'} + g(x)^{'}}\)
• \({(f(x) - g(x)) ^ {'} = f(x)^{'} - g(x)^{'}}\)
• \({(f(x) \cdot g(x)) ^{'} = f(x)^{'}g(x) + f(x)g(x)^{'}}\)
• \((\dfrac{f(x)}{g(x)})^{'} = \dfrac{f(x)^{'} g(x) - f(x)g(x)^{'}}{g(x)^2}\)

同时，我们将 \(f(x)^{''}\) 写作 \(f(x)^{(2)}\)，表示 \(f(x)\) 的二阶导数，也就是求导两次。

可以发现，\(f(x) = x^a\) 的 \(a\) 次导数就是就 \(a!\)。

一些常用导数

• \((x^{a})^{'} = ax^{a - 1}\)
• \((e^x)^{'} = e^x\)
• \((\sin x)^{'} = \cos x\)
• \((\cos x)^{'} = - \sin x\)

什么是泰勒展开

老祖宗告诉我们，计算一个函数，我们更喜欢计算多项式，而不喜欢计算 \(\sin x\) 这样的东西。

因此，我们希望找到一个多项式来代替 \(\sin x, \cos x\) 这样的函数。这种方法叫做泰勒展开。

先考虑一个简单情况，我们希望用多项式拟合 \(f(x) = \cos x\) 这个函数。记这个多项式为 \(g(x) = a_0 x^0 + a_1 x^1 + a_2 x^2 + \cdots + a_n x^n\)，把 \(g(x)^{(i)}\) 定义为 \(g(x)\) 的第 \(i\) 项。

首先在 \(x = 0\) 处进行拟合。首先要让 \(g(0)\) 的函数值与 \(f(0)\) 相等吧？所以 \(g(0)^{(0)} = f(0) = 1\)。我们称之为线性逼近。

拟合函数如下：

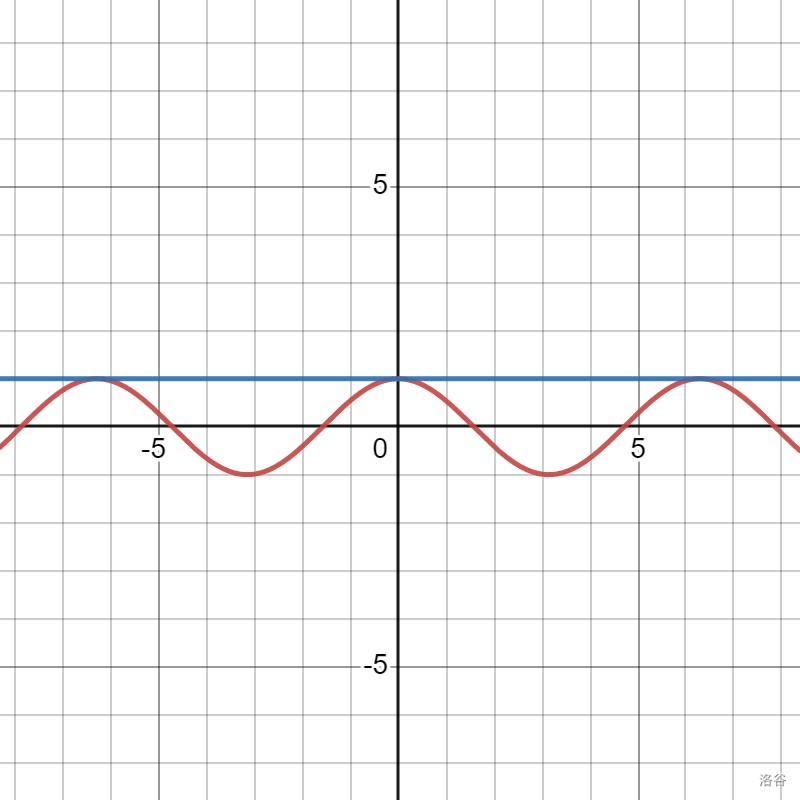
可以发现，\(g(x)\) 与 \(f(x)\) 拟合度很差，仅在 \(x = 0\) 时函数值相等，还需要继续改进。

我们可以让 \(g(0)^{(1)}\) 与 \(f(0)\) 导数相等，不妨设 \(g(x)^{(1)} = \dfrac{a_i}{1!} x^1\)，\(a_i = f(0)^{(1)} = (\cos 0)^{(1)} = - \sin 0 = 0\)。所以 \(g(x)^{(1)} = 0\)。我们称为一次逼近。这时 \(g(x) = 1\)。

同样的，我们可以推广到二次逼近，也就是让 \(a_2 = f(0)^{(2)} = (\cos 0)^{(2)} = - \cos 0 = -1\)。这时 \(g(x) = 1 + \dfrac{-1}{2!} x^2\)。拟合函数如下：

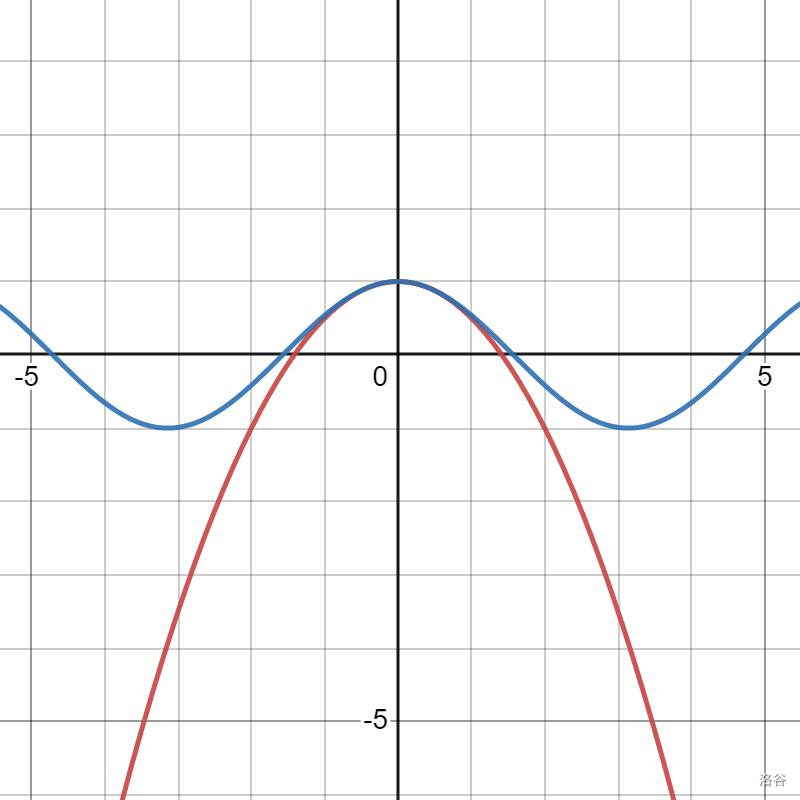
可以发现，这时的拟合比第一次准确的多。

当然，我们也可以考虑四次逼近，八次逼近。四次逼近时要让 \(a_3 = f(0) ^ {(3)}, a_4 = f(0)^{(4)}\)。

这里给出四次逼近的式子：

\[g(x) = \dfrac{f(0)}{0!} x^0 + \dfrac{f(0)^{(1)}}{1!} x^1 + \dfrac{f(0)^{(2)}}{2!} x^2 + \dfrac{f(0)^{(3)}}{3!} x^3 + \dfrac{f(0)^{(4)}}{4!} x^4 \]

即为：

\[g(x) = \dfrac{1}{0!} x^0 + \dfrac{0}{1!} x^1 + \dfrac{-1}{2!} x^2 + \dfrac{0}{3!} x^3 + \dfrac{1}{4!} x^4 \]

\[g(x) = \dfrac{1}{0!} x^0 - \dfrac{1}{2!} x^2 + \dfrac{1}{4!} x^4 \]

拟合函数图像如下：

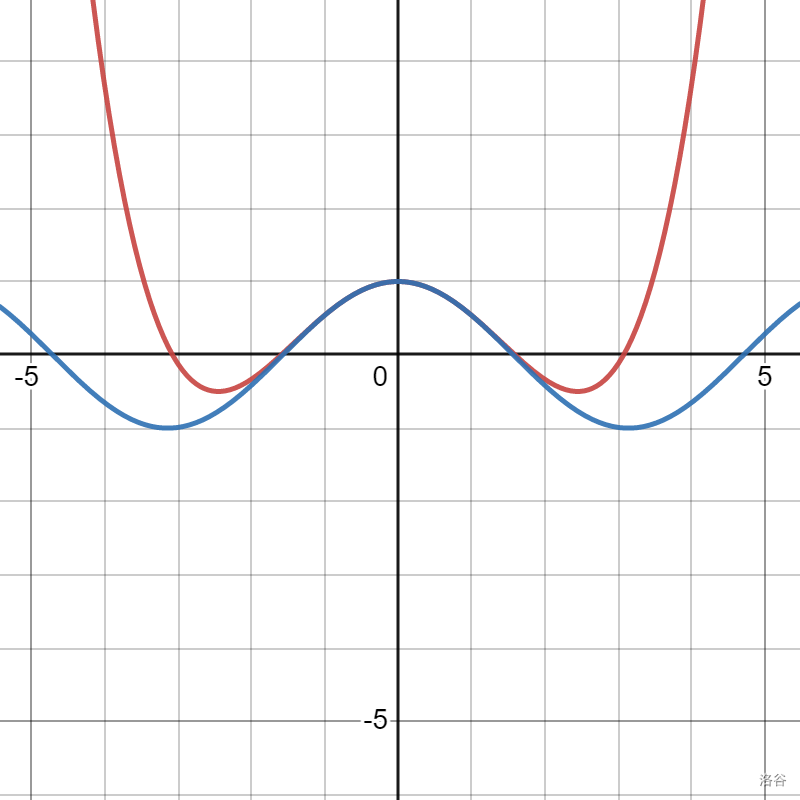
同样的，八次逼近的图像如下：

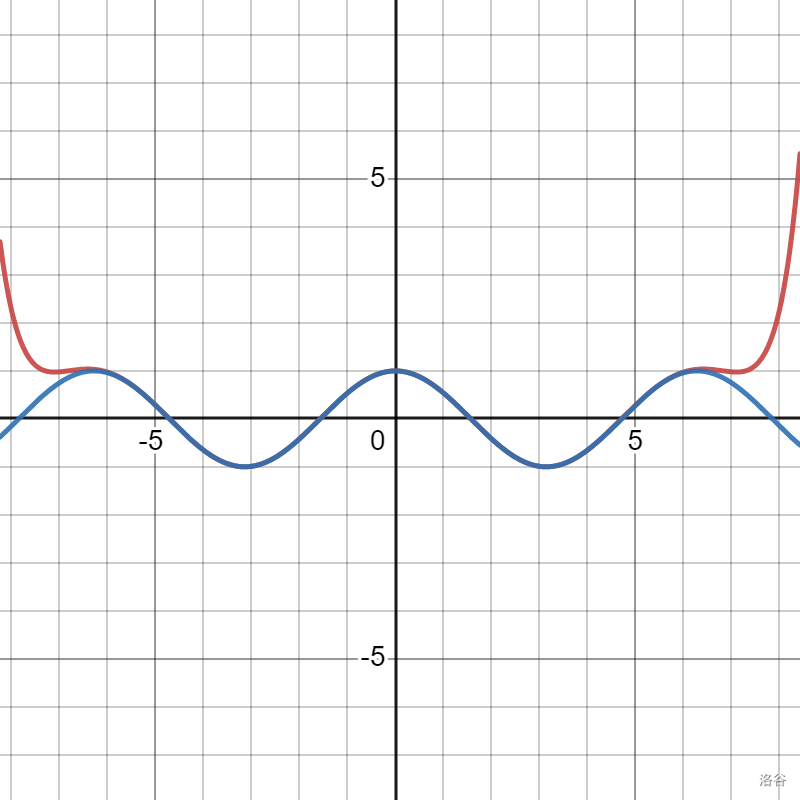
在这里有 \(n\) 小于等于 \(16\) 的交互式图像。cos x 的泰勒展开

可以发现，随着 \(n\) 的增大，\(g(x)\) 的图像无限逼近 \(f(x)\)。当 \(n \rightarrow + \infin\)，两个函数的曲率相等。因此，可以将展开写成这样的形式：

\[g(x) = \sum_{i = 0}^{ + \infin} (-1) ^ i + \dfrac{x^{2i}}{(2i)!} \]

这种从 \(0\) 开始展开的式子被称为 麦克劳林展开。一般来说，麦克劳林展开有公式

\[g(x) = \sum_{i = 0}^{n} \dfrac{f(0)^{(i)}}{i!} x^i + R_n(x) \]

这里的 \(R_nx\) 指皮亚诺余项，可以理解为误差。

常见的麦克劳林展开有下面几种：

• \(\sin x = \sum_{i = 0}^{ + \infin} (-1)^i \dfrac{(x^{2i + 1})}{(2i + 1)!} + R_n(x)\)
• \(\cos x = \sum_{i = 0}^{ + \infin} (-1) ^ i \dfrac{x^{2i}}{(2i)!} + R_n(x)\)
• \(e ^ x = \sum_{i = 0}^{ + \infin} \dfrac{x^i}{i!} + R_n(x)\)