leetcode516. 最长回文子序列

题目链接：https://leetcode-cn.com/problems/longest-palindromic-subsequence/

子序列和子串的不同就是子序列可以不连续，可以任意删除中间的某些字符，但顺序依然无法改变。

对于一个长度大于2的回文序列来说，去掉首尾两个字符，该序列依然是回文的，所以本题可以用动态规划求解。

五部曲：

1. 确定dp数组的定义以及下标的含义

   dp[i][j]表示字符串s下标[i,j]范围内的最长回文子序列的长度。

2. 递推公式

   前面说过了任意回文序列去掉首尾两个字符依然回文，所以对于dp[i][j]就可以通过dp[i+1][j-1]来推导。

   这里要分两种情况：

   • 如果s[i] = s[j]，那么 dp[i][j] = dp[i+1][j-1] + 2;

     首尾字符相同，加上依然回文，所以直接+2

   • 如果s[i] != s[j]，那么 dp[i][j] = max(dp[i+1][j], dp[i][j-1]);

     如果不相同，那就在首尾两个字符中选一个看看哪个可以使回文序列变长，取两者中较大的即可。

3. dp数组的初始化

   因为是回文序列嘛，肯定要求 0<i≤j<n ，那么所有i > j的 dp[i][j]=0;

   而对于i=j的，因为一个字符就相当于长度为1的回文序列，所以对于0≤i<n，dp[i][i] = 1;

   对于 i<j 的，也初始化为0，遍历的时候计算。

4. 遍历顺序

   

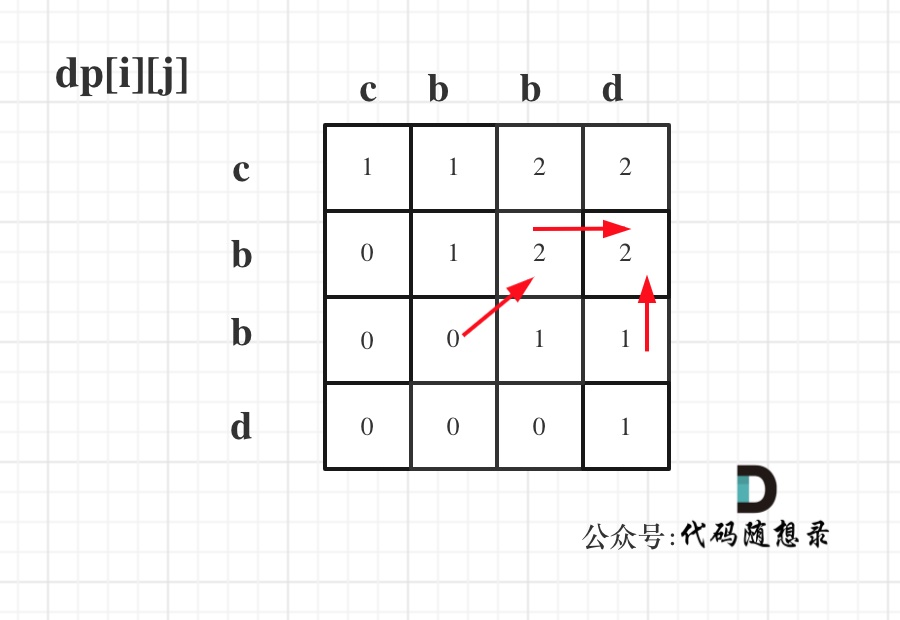
   根据这个图，可以看出dp[i][j]要么是通过i+1（下面一行）要么是通过j-1（左边一列）得出的，所以遍历顺序是i从大到小，j从小到大

5. 举例推导dp数组

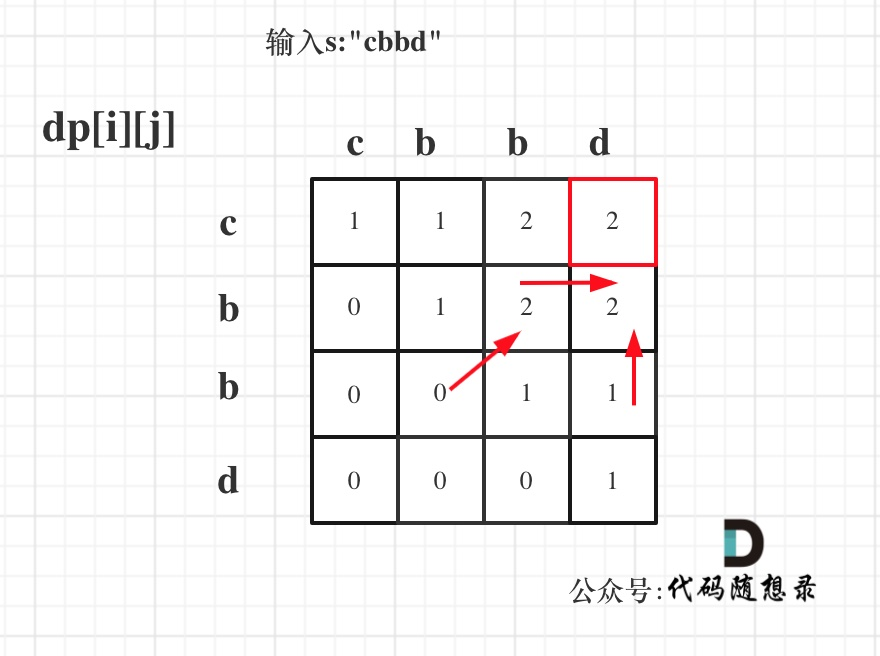
遍历之后的状态如图所示，最终返回结果为dp[0][3]

C++代码：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        for(int i = n - 1; i >= 0; i--){
            dp[i][i] = 1;
            for(int j = i + 1; j < n; j++){
                if(s[i] == s[j]){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][n - 1];
    }
};