Machine Learning Notes Ⅲ

欠拟合与过拟合

欠拟合：特征选择不够或所选的函数次数过低导致拟合不完全，一些内在性质没有被反映出来。

过拟合：特征选择过多或所选的函数次数过高导致拟合仅仅反映了样本数据的特殊性质，忽略了内在联系。

解决方法：特征选择算法、非参数学习算法。

参数学习算法与非参数学习算法

参数学习算法("Parametric" learning algorithm)：
一种有固定数目的参数来进行数据拟合的算法。训练完成后可以得到一组参数，在对新数据进行预测时就不再需要训练数据。

非参数学习算法("Non-parametric" learning algorithm)：
一种n（参数数量）随m（样本数量）增长所增长（一般为线性增长）的数据拟合算法。在每次预测时还要依赖之前的训练数据进行重新训练。

局部加权回归(locally weighted regression)

它是一种非参数学习算法。基本思路是：假如现在要对x这个位置进行预测，我们希望能够降低那些离x较远的样本对结果的影响。所以通过对优化判据进行一些修改，给每个样本增加一个权重，变成最小化\(J(\theta)=\sum_{i=1}^{m}{w_{(i)}*(h_{\theta}(x^{(i)})-y^{(i)})^2}\)。其中\(w_{(i)}\)与\(x^{(i)}\)和\(x\)的距离相关，具体关系式为\(w_{(i)}=exp(-\frac{(x^{(i)}-x)^2}{2\tau^2}) \quad (\tau \gt 0)\)，公式中\(\tau\)越大，距离远的样本的权重越大。

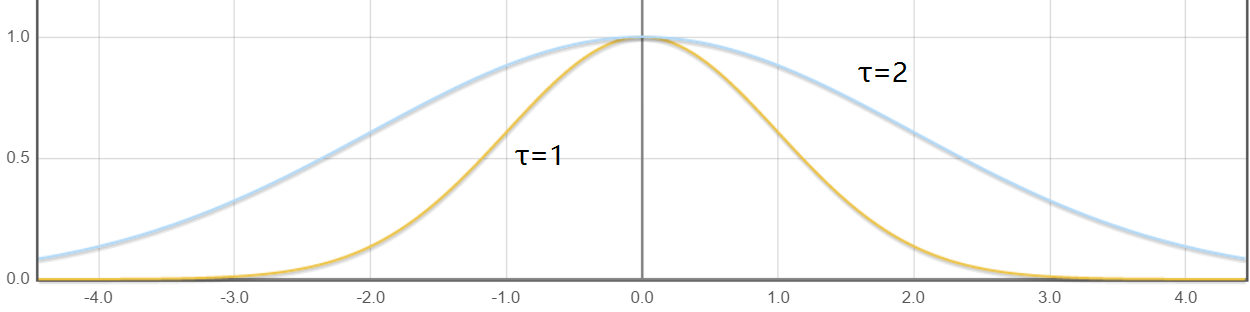
以上是\(\tau\)分别等于\(1,2\)时\(w\)函数的图像。

为什么使用最小二乘

在之前线性回归时，我们直接使用\(J(\theta)=\frac12 *\sum_{i=1}^m{(h_{\theta}(x^{(i)})-y^{(i)})^2}\)作为优化判据，现在我们尝试对它进行概率上的证明。

首先，我们假设\(y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}\)，其中\(\epsilon\,\)是对未建模效应的捕获。可以将\(\epsilon\,\)看成是许多互相独立的随机变量的综合影响，根据中心极限定理可以推测\(\epsilon\,\)满足高斯分布，我们假设\(\epsilon \sim N(0,\sigma^2)\)。
那么\(P(\epsilon^{(i)})=\frac1{\sqrt{2\pi}\sigma}exp(-\frac{(\epsilon^{(i)})^2}{2\sigma^2})\)，可以计算出\(P(y^{(i)}\mid x^{(i)};\theta)=\frac1{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})\)。
所以\(P(y^{(i)}\mid x^{(i)};\theta) \sim N(\theta^Tx^{(i)},\sigma^2)\)。
定义似然函数\(L(y=A\mid x=B)\)为当\(x=B\)时，\(y=A\)的似然性大小。注意似然性不是概率，因为\(y\)可能不是一个随机变量而是一个未知的常量。\(L\)函数没有取值范围的限制，仅仅用它的相对大小来描述当\(x=B\)时\(y=A\)的“合理性”。
令\(L(\theta)\)来表示在当前样本的情况下，系数为\(\theta\)的似然性。则$$L(\theta)=P(\vec y \mid x;\theta)=\prod_{i=1}^{m{\frac1{\sqrt{2\pi}\sigma}exp(-\frac{(y}-\theta^Tx)^2}{2\sigma2})}$$所以我们的目标就是找到一个\(\theta\)的取值使得似然性最大。令\(l(\theta)=\ln{L(\theta)}\)，原问题就变成了最大化\(l(\theta)\)。

\[\begin{align*} \\ l(\theta)&=\ln{L(\theta)} \\ &=\ln{(\prod_{i=1}^m{\frac1{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})})} \\ &=\sum_{i=1}^m{\ln{\frac1{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})}} \\ &=m*\ln{\frac1{\sqrt{2\pi}\sigma}}+\sum_{i=1}^m{\ln{(exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}))}} \\ &=m*\ln{\frac1{\sqrt{2\pi}\sigma}}+\sum_{i=1}^m{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}} \\ \end{align*} \]

考虑到\(\sigma\)为一个正常量，所以最大化\(l(\theta)\)就是最小化\(\frac12\sum_{i=1}^m{(y^{(i)}-\theta^Tx^{(i)})^2}\)，也就是我们所定义的\(J\)函数。

第一个分类算法

因为\(y \in \lbrace 0,1\rbrace\)，所以我们令估计函数的取值范围为\([0,1]\)。
基于某种原因，我们选择了sigmoid函数：\(g(z)=\frac1{1+e^{-z}}\)。
令\(h_\theta(x)=g(\theta^Tx)=\cfrac1{1+e^{-\theta^Tx}}\)，\(h_\theta(x)\)的值代表我们对于这个数据，输出结果为\(1\)的概率。
同样做概率分析：
有\(P(y=1\mid x;\theta)=h_\theta(x)\)，\(P(y=0\mid x;\theta)=1-h_\theta(x)\)。
我们令\(P(y\mid x;\theta)={h_\theta(x)}^y {(1-h_\theta(x))}^{1-y}\)。当\(y=1\)时，这个式子的结果等于\(h_\theta(x)\)；当\(y=0\)时，这个式子的结果等于\(1-h_\theta(x)\)。
同样：

\[\begin{align*} \\ L(\theta)&=P(\vec y\mid x;\theta) \\ &=\prod_{i=1}^m{P(y^{(i)}\mid x^{(i)};\theta)} \\ &=\prod{i=1}^m{ {h{\theta}(x^{(i)})}^{y^{(i)}}(1-h_\theta(x^{(i)}))^{(1-y^{(i)})}} \\ \end{align*}$$$$l(\theta)=\ln{L(\theta)}=\sum_{i=1}^m{y^{(i)}\ln{h_\theta(x^{(i)})}}+\sum_{i=1}^m{(1-y^{(i)})\ln{(1-h_\theta(x^{(i)}))}} \]

现在，我们的目标就是求出一组\(\theta\)使得\(l(\theta)\)最大。我们将梯度下降法做一些修改（将每次迭代的等式里的减号变成加号），就可以直接处理这个问题。
这里直接给出\(\frac{\partial l(\theta)}{\partial \theta_j}=\sum_{i=1}^m{(y^{(i)}-h_\theta(x^{(i)}))x^{(i)}_j}\)。
同样的，在样本数量较大时，也可以使用随机梯度下降法来减少算法运行时间。

感知器算法(Perceptron algorithm)

感知器算法是另一种用于分类问题的学习型算法。这次我们定义了一个更加和问题贴近的函数

\[g(z)=\begin{cases} 1, & z \geq 0 \\ 0, & \text{otherwise} \\ \end{cases} \]

令\(h_\theta(x)=g(\theta^Tx)\)。
课程中只提到了这个算法使用了与之前不同的学习规则，没有给出优化判据\(J(\theta)\)，而是直接给出了对其求偏导的结果\(\frac{\partial J(\theta)}{\partial \theta_j}=\sum_{i=1}^m{(y^{(i)}-h_\theta(x^{(i)}))*x^{(i)}_j}\)。