Hamming code-汉明码(中文)

汉明码

维基百科，自由的百科全书

 

本文提供了参考文献列表，但其来源尚不清楚，因为它没有足够的内联引文。请通过引入更精确的引用来帮助改进本文。 （2013年3月）（了解如何以及何时删除此模板消息）

二进制汉明码
海明（7,4）代码（r = 3）
而得名	理查德·汉明
分类
类型	线性块代码
块长	2 - [R - 1，其中[R ≥2
讯息长度	2 r − r − 1
率	1 − r/（2 r − 1）
距离	3
字母大小	2
符号	[2 r − 1，2 r − r − 1，3] 2代码
性质
完美的代码
v Ť Ë

在电信领域中，汉明码是一类线性纠错码。汉明码最多可以检测两位错误或纠正一位错误，而无需检测未纠正的错误。相反，简单的奇偶校验码不能纠正错误，并且只能检测到奇数个错误位。汉明码是完美的代码，也就是说，汉明码的块长和最小距离为三，可以实现最高的编码率。^[1]理查德·汉明（Richard W. Hamming）于1950年发明了汉明代码，作为一种自动纠正打孔卡引入的错误的方法 读者。Hamming在他的原始论文中阐述了他的总体思想，但特别关注了Hamming（7,4）代码，该代码将三个奇偶校验位添加到四个数据位。^[2]

用数学术语来说，汉明码是一类二进制线性码。对于每个整数 r ≥ 2 存在一个分组长度 n = 2^r - 1 、n = 2^r - r - 1 的编码。因此，汉明码的码率为R = k / n = 1- r /（2 ^r -1），对于最小距离为3的代码（即，从任意距离到位所需的最小位数的变化）是最高的代码字到任何其他代码字都是3），块长度（或分组长度）为2^r − 1。通过列出所有长度为 r的非零列来构造汉明码的奇偶校验矩阵，这意味着汉明码的对偶码是缩短的Hadamard码。奇偶校验矩阵具有以下特性：任意两列都是成对线性独立的。

由于汉明码添加到数据的冗余性有限，因此仅在错误率较低时，它们才能检测和纠正错误。在计算机内存（ECC内存）中就是这种情况，在这种情况下，极少出现误码并且广泛使用汉明码。在这种情况下，经常使用具有一个额外奇偶校验位的扩展汉明码。扩展的汉明码实现的汉明距离为4，这使解码器可以区分何时最多出现一位错误和何时出现两位错误。从这个意义上讲，扩展的汉明码是单错误纠正和双错误检测，缩写为SECDED ^{[ 需要引用 ]}。

内容

• 1历史
  • 1.1汉明之前的代码
    • 1.1.1奇偶校验
    • 1.1.2五分之二的代码
    • 1.1.3重复
• 2个汉明码
  • 2.1通用算法
• 3个具有额外奇偶校验的汉明码（SECDED）
• 4[7,4]汉明码
  • 4.1G和H的构造
  • 4.2编码
  • 4.3[7,4]带有附加奇偶校验位的汉明码
• 5另请参见
• 6笔记
• 7参考
• 8个外部链接

历史

哈明码的发明者理查德·汉明（Richard Hamming）在1940年代后期在贝尔实验室（Bell Labs）研发了Bell Model V计算机，这是一种基于机电继电器的机器，周期时间以秒为单位。输入内容通过打孔的纸带进给，该纸带宽八分之七英寸，每行最多六个孔。在工作日中，当检测到继电器故障时，机器将停止运转并闪烁，以使操作员可以纠正问题。在下班时间和周末，当没有操作员时，机器只是继续进行下一个工作。

Hamming在周末工作，由于发现错误而不得不从头开始重新启动程序，对此感到越来越沮丧。海明在录音带中接受采访时说：“所以我说，'该死，如果机器能够检测到错误，为什么它不能找到错误的位置并进行纠正呢？'” ^[3]在接下来的几年中，他致力于纠错问题，开发了功能越来越强大的算法。1950年，他发表了现在称为汉明码的汉明码，该代码至今仍在ECC存储器等应用程序中使用。

汉明之前的代码

在汉明码之前使用了许多简单的错误检测码，但是在相同的空间开销下，没有一个像汉明码那样有效。

奇偶校验

主条目：奇偶校验位

奇偶校验添加一个位，该位指示前面的数据中的个数（值为1的位位置）是偶数还是奇数。如果传输中的位数更改为奇数，则消息将更改奇偶校验，并且此时可以检测到错误；但是，更改的位可能是奇偶校验位本身。最常见的约定是，奇偶校验值为1表示数据中奇数个1，奇偶校验值为零表示奇偶数个。如果更改的位数为偶数，则校验位将有效，并且不会检测到错误。

此外，奇偶校验不会指示哪位包含错误，即使它可以检测到它也是如此。数据必须全部丢弃，并从头开始重新传输。在嘈杂的传输介质上，成功的传输可能需要很长时间或可能永远不会发生。但是，尽管奇偶校验的质量很差，但由于它仅使用单个位，因此此方法的开销最少。

五分之二的代码

主条目：五分之二的代码

五分之二的代码是一种编码方案，它使用正好由三个0和两个1组成的五个位。这提供了十种可能的组合，足以代表数字0–9。该方案可以检测所有单个位错误，所有奇数位错误和一些偶数位错误（例如两个1位的翻转）。但是，它仍然无法纠正任何这些错误。

重复

主条目：三重模块化冗余

当时使用的另一个代码会重复每个数据位多次，以确保正确发送。例如，如果要发送的数据位为1，则n = 3 重复码将发送111。如果接收到的三个位不相同，则在传输期间发生错误。如果通道足够干净，则大多数情况下每个三元组仅更改一位。因此，001，010和100分别对应于0位，而110，101和011对应于1位，其中更多的相同数字（“ 0”或“ 1”）指示什么数据位应该是。在出现错误的情况下具有这种能力来重构原始消息的代码称为纠错码。该三重重复码是具有m = 2的汉明码，因为有两个奇偶校验位，而2 ^2-2-1 = 1个数据位。

但是，此类代码无法正确修复所有错误。在我们的示例中，如果通道翻转两位并且接收器得到001，则系统将检测到错误，但得出的结论是原始位为0，这是不正确的。如果将位串的大小增加到四个，我们可以检测到所有两位错误，但无法纠正它们（奇偶校验位的数量是偶数）；在五个位上，我们可以检测并纠正所有两位错误，但不能检测并纠正所有三位错误。

此外，增加奇偶校验位字符串的大小效率很低，在我们的原始情况下将吞吐量降低了三倍，并且随着我们增加每个位的重复次数以检测和纠正更多错误，效率急剧下降。

 

通用算法

以下通用算法为任意数量的位生成单错误纠正（SEC）代码。主要思想是选择纠错位，使得index-XOR（所有包含1的位的XOR）为0。我们将位置1、10、100等（二进制）用作错误-纠错位，以确保可以设置纠错位，以使整个消息的索引XOR为0。如果接收方接收到的索引XOR为0的字符串，则它们可以得出结论：没有损坏，否则，index-XOR表示损坏位的索引。

以下步骤实现了该算法：

1. 从1：1、2、3、4、5、6、7等位开始编号。
2. 以二进制形式写入位数：1、10、11、100、101、110、111等。
3. 所有为2的幂的位位置（在其位置的二进制形式中只有一个1位）是奇偶校验位：1、2、4、8等（1、10、100、1000）
4. 所有其他位位置，其中两个或更多1位为二进制形式的位置，均为数据位。
5. 每个数据位包含在2个或更多奇偶校验位的唯一集合中，这由其位位置的二进制形式确定。
   1. 奇偶校验位1覆盖所有设置了最低有效位的位：位1（奇偶校验位本身），3、5、7、9等。
   2. 奇偶校验位2覆盖设置了第二个最低有效位的所有位位置：位2（奇偶校验位本身），3、6、7、10、11等。
   3. 奇偶校验位4覆盖具有最低位的第三位的所有位位置：位4-7、12-15、20-23等。
   4. 奇偶校验位8覆盖具有最低位的第四位的所有位位置：位8-15、24-31、40-47等。
   5. 通常，每个奇偶校验位覆盖奇偶校验位置和位位置的按位与不为零的所有位。

如果要编码的数据字节为10011010，则数据字（使用_表示奇偶校验位）将为__1_001_1010，代码字为011100101010。

奇偶校验的形式无关紧要。即使是奇偶校验在数学上也更简单，但实际上没有区别。

可以直观地显示此一般规则：

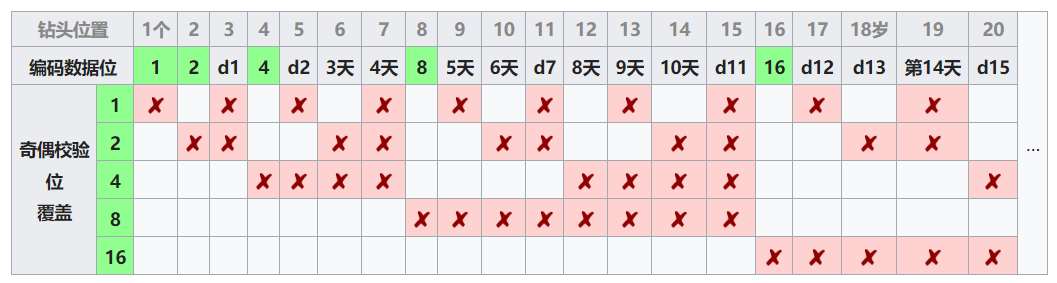
仅显示了20个编码位（5个奇偶校验，15个数据），但是该模式无限期地继续。从汉字检查中可以看到的关于汉明码的关键是，任何给定的位都包含在唯一的一组奇偶校验位中。要检查错误，请检查所有奇偶校验位。错误模式称为错误校验子，用于标识错误位。如果所有奇偶校验位都正确，则没有错误。否则，错误奇偶校验位的位置总和将识别错误位。例如，如果位置1、2和8的奇偶校验位指示错误，则位1 + 2 + 8 = 11是错误的。如果只有一个奇偶校验位指示错误，则奇偶校验位本身就是错误的。

 如您所见，如果您有m个奇偶校验位，则可以覆盖从1到1的位。2^m-1。如果我们减去奇偶校验位，我们剩下2^m-m-1，我们可以用于数据的位。随着m的变化，我们得到所有可能的汉明码：

 

具有附加奇偶校验的汉明码（SECDED）

汉明码的最小距离为3，这意味着解码器可以检测和纠正单个错误，但无法区分某个代码字的双比特错误与不同代码字的单个比特错误。因此，除非没有尝试校正，否则某些双位错误将被错误地解码，就好像它们是单位错误一样，因此无法被检测到。

为了弥补这一缺点，可以通过额外的奇偶校验位扩展汉明码。^{[ 引证需要 ]}通过这种方式，有可能增加汉明码的最小距离为4，其允许解码器单比特差错和双比特错误之间进行区分。因此，解码器可以检测和纠正单个错误，同时检测（但不纠正）双重错误。

如果解码器不尝试纠正错误，则可以可靠地检测到三位错误。如果解码器确实纠正了错误，则某些三重错误将被误解为单个错误，并被“纠正”为错误的值。因此，纠错是在确定性（可靠地检测三比特错误的能力）和弹性（面对单个比特错误的情况下保持功能的能力）之间的权衡。

这种扩展的汉明码在计算机存储系统中很流行^{[ 需要引用 ]}，在这里它被称为SECDED（缩写为单错误纠正，双重错误检测）^{[ 需要引用 ]}。尤其流行的是（72,64）码，截断的（127,120）Hamming码加上一个额外的奇偶校验位^{[ 需要引用 ]}，该空间具有与（9,8）奇偶校验码^{[ 需要引用 ]}相同的空间开销。

 

 

 

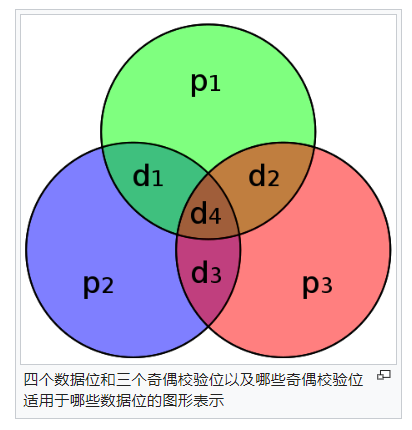
[7,4]汉明码

主条目：汉明（7,4）

1950年，汉明（Hamming）推出了[7,4]汉明代码。通过添加三个奇偶校验位，它将四个数据位编码为七个位。它可以检测和纠正单位错误。通过添加整体奇偶校验位，它还可以检测（但不正确）双位错误。

G和H的构造

最后，可以通过以下操作将这些矩阵突变为等效的非系统代码：^[4]

• 列排列（交换列）
• 基本行操作（用行的线性组合替换行）

 

编码

[7,4]带有附加奇偶校验位的汉明码

G的非系统形式可以进行行缩减（使用基本行操作）以匹配此矩阵。

第四行的加法有效地计算了所有码字位（数据和奇偶校验）的总和，作为第四奇偶校验位。

例如，将1011编码（在本节的开头使用G的非系统形式）为01 1 0 011 0，其中蓝色数字为数据；红色数字是来自[7,4] Hamming码的奇偶校验位；绿色数字是[8,4]码加上的奇偶校验位。绿色数字使[7,4]码字的奇偶校验均匀。

最后，可以证明最小距离已从[7,4]代码中的3增加到[8,4]代码中的4。因此，该代码可以定义为[8,4]汉明代码。

要解码[8,4]汉明码，请首先检查奇偶校验位。如果奇偶校验位指示错误，则单次纠错（[7,4]汉明码）将指示错误位置，“无错误”则指示奇偶校验位。如果奇偶校验位正确，则单个错误纠正将指示两个错误位置的（按位）异或。如果位置相等（“无错误”），则不会发生双位错误，或者已将自身取消。否则，将发生双位错误。