查找之——B树、B+树的概念及性质+答题技巧（必背几句，考试不慌，稳得一匹）【多图！多动图！多耗费流量警告！！！预计消耗20M+流量】
2019/11/21
B树，又称多路平衡查找树，B树中所有结点的孩子结点数的最大值称为B树的阶。
一颗m阶B树或是空树，或是满足如下特性的m叉树：
1）树中每个结点至多有m棵子树、m-1个关键字。
2）若根节点不是终端节点（非叶子节点），则至少有两棵子树、1个关键字（由 1）得到：2阶-1=1个关键字）。
3）除根节点外的所有非叶结点（除去第一行和最后一行元素），
至少有${\left \lceil m/2 \right \rceil}$棵子树、${\left \lceil m/2 \right \rceil}$-1个关键字。
给出阶数m和关键字n,高度h的B树→求树的最大高度和最小高度，背住以下公式，很快求出：
$\log _{m}(n+1)\leqslant h\leqslant \log_{\left \lceil m/2 \right \rceil}(\frac{n+1}{2})+1$
推导过程：
$n\leq (m-1)(1+m+m^{2}+...+m^{h-1})$
得到树的最小高度。
下面是最大高度
第h+1那层，叶结点的那层有$2(\left \lceil m/2 \right \rceil)^{h-1}$个结点。
因为在B树中，它的关键字个数为n的话，则它的叶结点，也就是查找失败结点，数量为n+1。
对应的失败结点就是对应着不存在该B树上的值的那一个区间，
那么对应有n个关键字，就会有n+1个区间，所以它的失败结点数量为n+1。
$2(\left \lceil m/2 \right \rceil)^{h-1} \leqslant n+1$ 就可以计算出它的最大取值了。
得到如下结果：
$\log _{m}(n+1)\leqslant h\leqslant \log_{\left \lceil m/2 \right \rceil}(\frac{n+1}{2})+1$
树的几个通用性质也务必牢记：
①树中的结点数 = 所有结点的度数 + 1
②度为m的树中，第 i 层上至多有mi - 1个结点（i ≥1）
③高度为h的m叉树至多有（mk-1)/(m-1)个结点。
④具有n个结点的m叉树的最小高度为$\left \lceil \log _{m} (n(m-1)+1)\right \rceil$
注：背住以上三条性质+最后在B/B+树中，求树高的公式+树的通用性质，则答题无惑矣😊🎉🎉🎉，尤其注意红色加粗部分，至少和至多的运用。
非叶结点的结构：
| n | P0 | K1 | P1 | K2 | P2 | ...Kn | Pn |
Ki(i=1,2,...n)为结点的关键字，K1<K2<K3<.....<Kn。
Pi(i=1,2,...n) 为子树根节点的指针，
Pi-1所指子树的关键字均小于Ki
Pi 所指子树关键字均大于Ki
所有叶结点都出现在同一层次上，并不带任何信息
几种操作：
一、查找
①在B树中找结点 磁盘
②在结点中找关键字 内存
二、插入
①定位
②插入
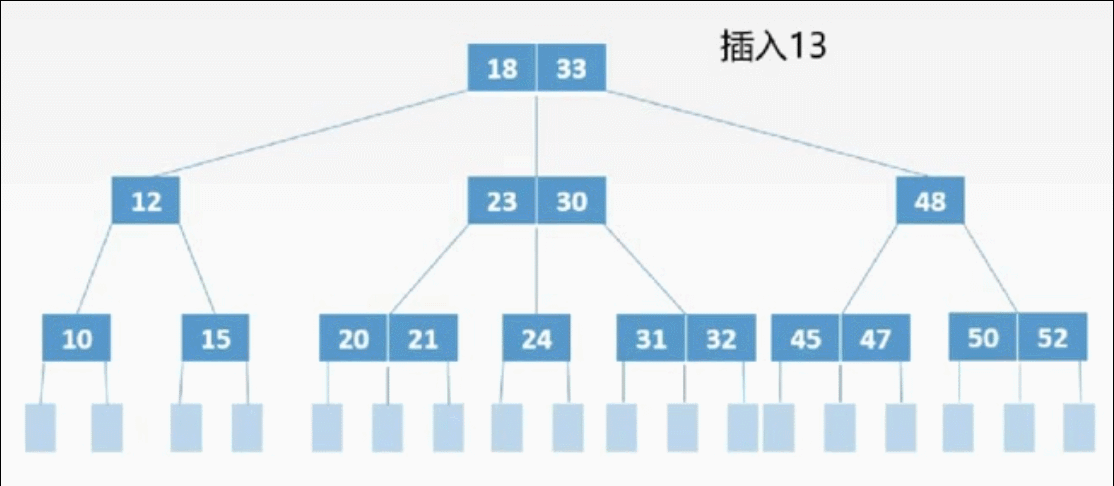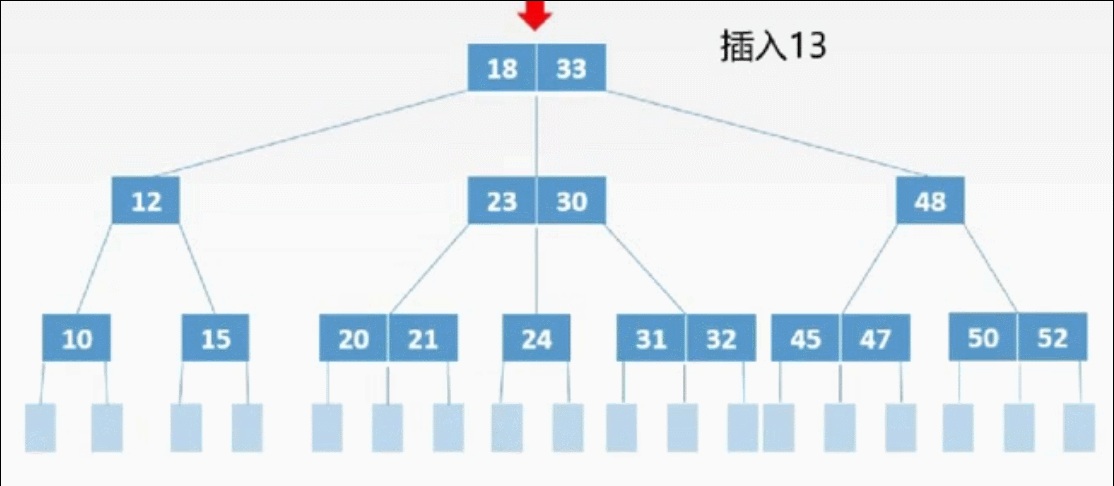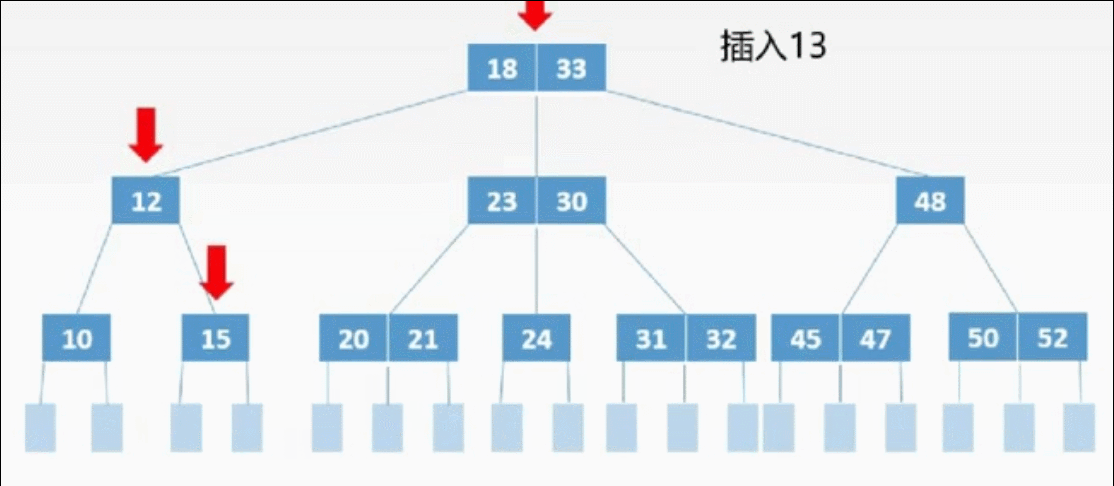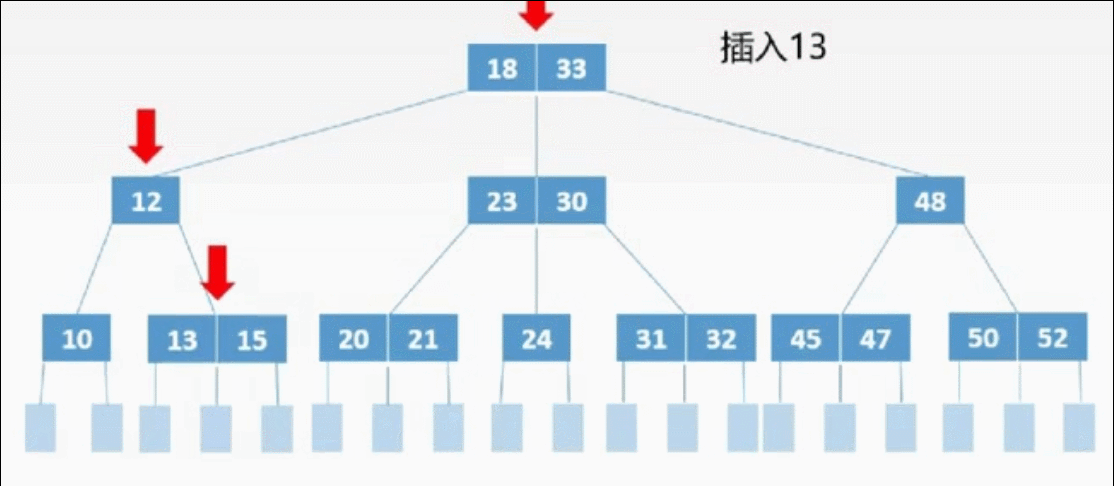
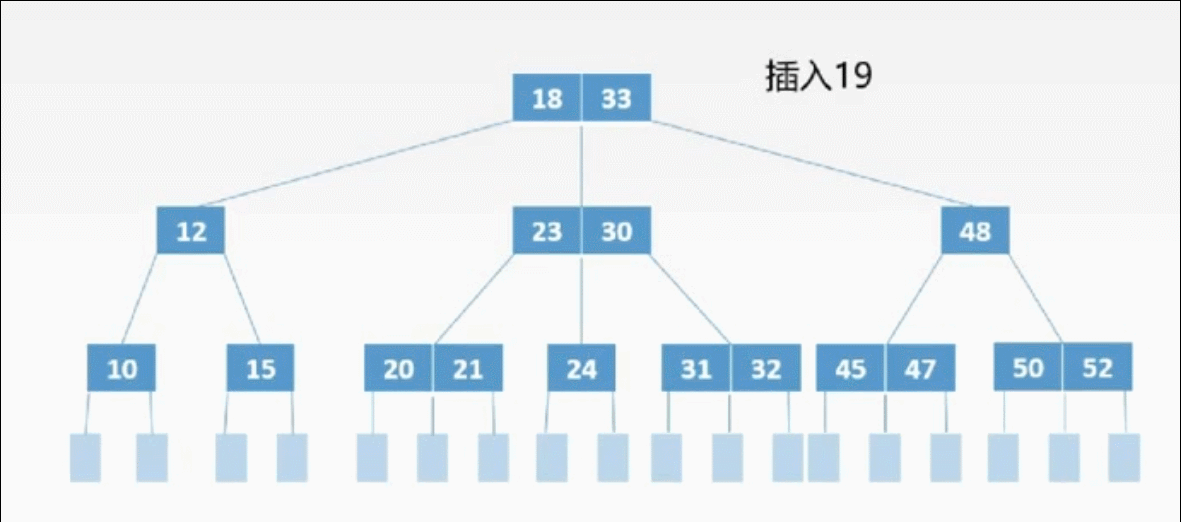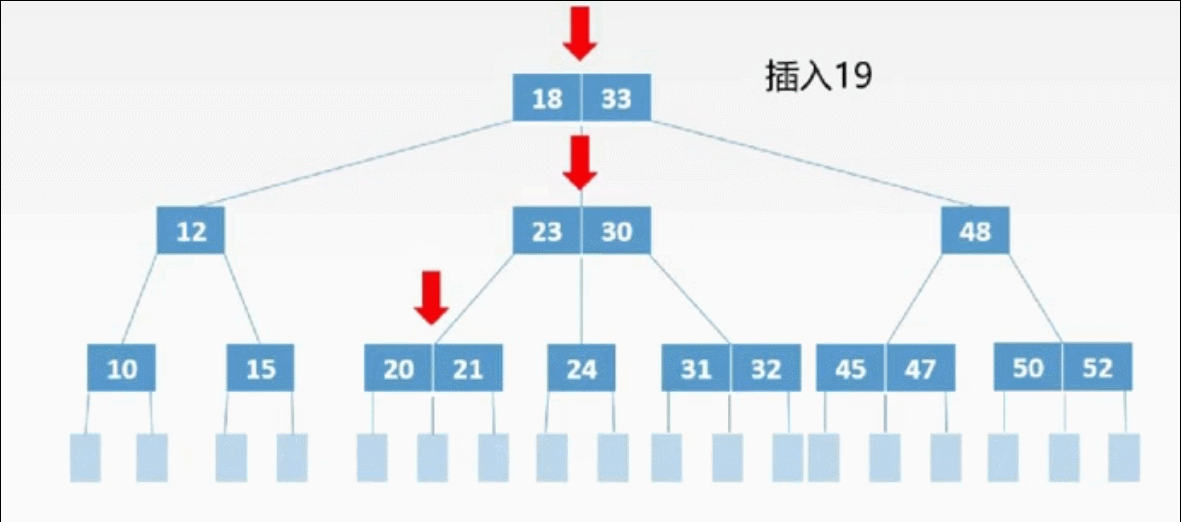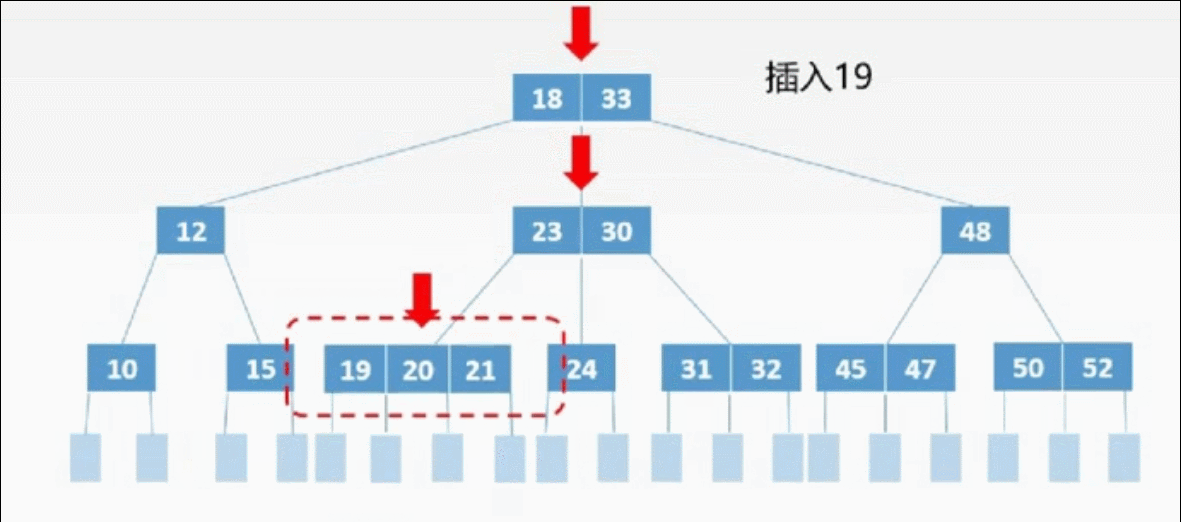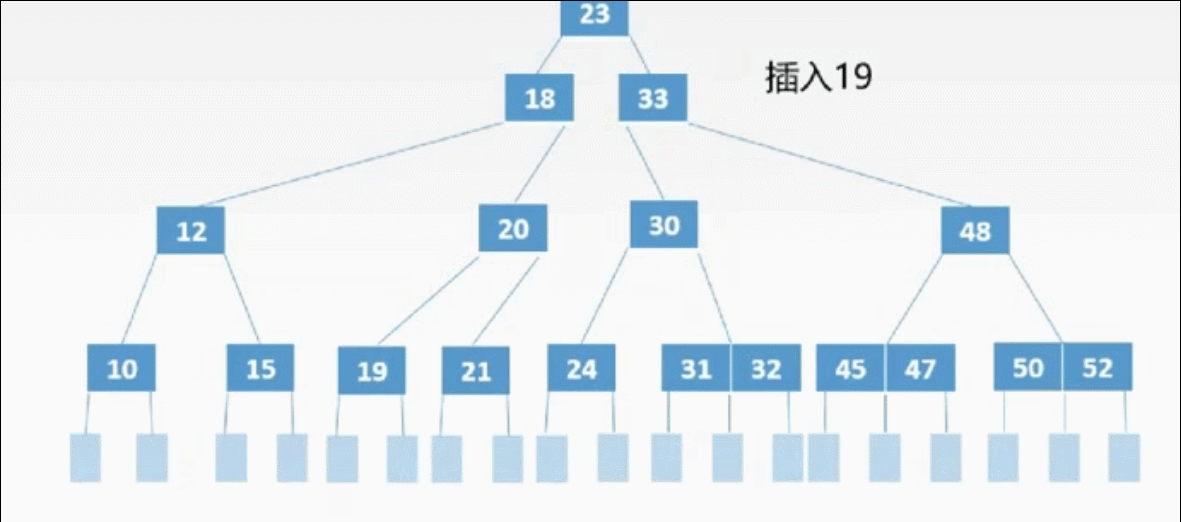
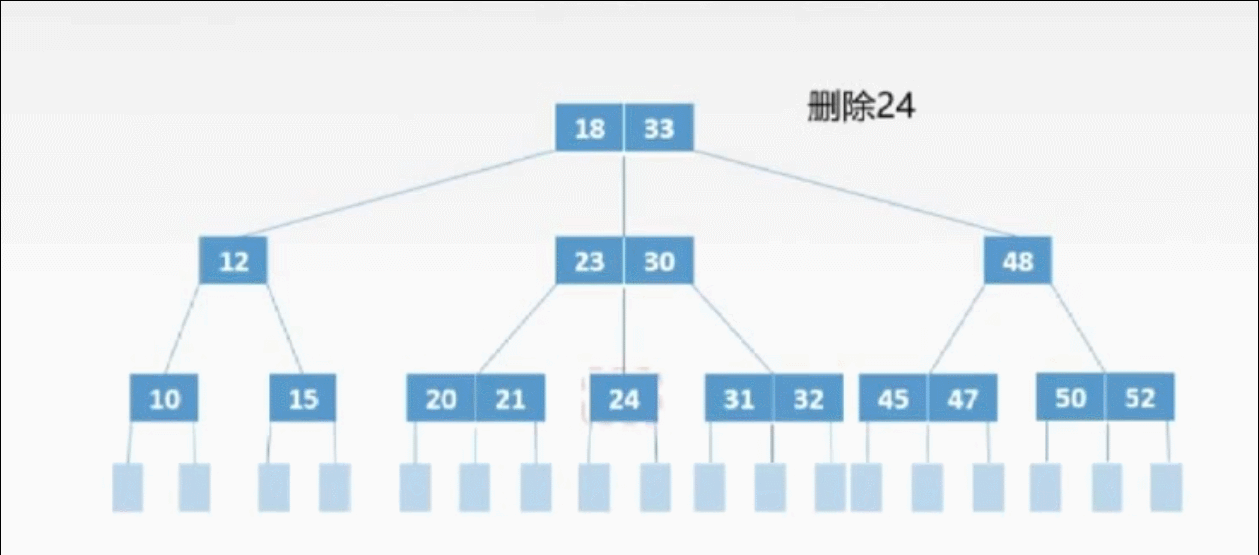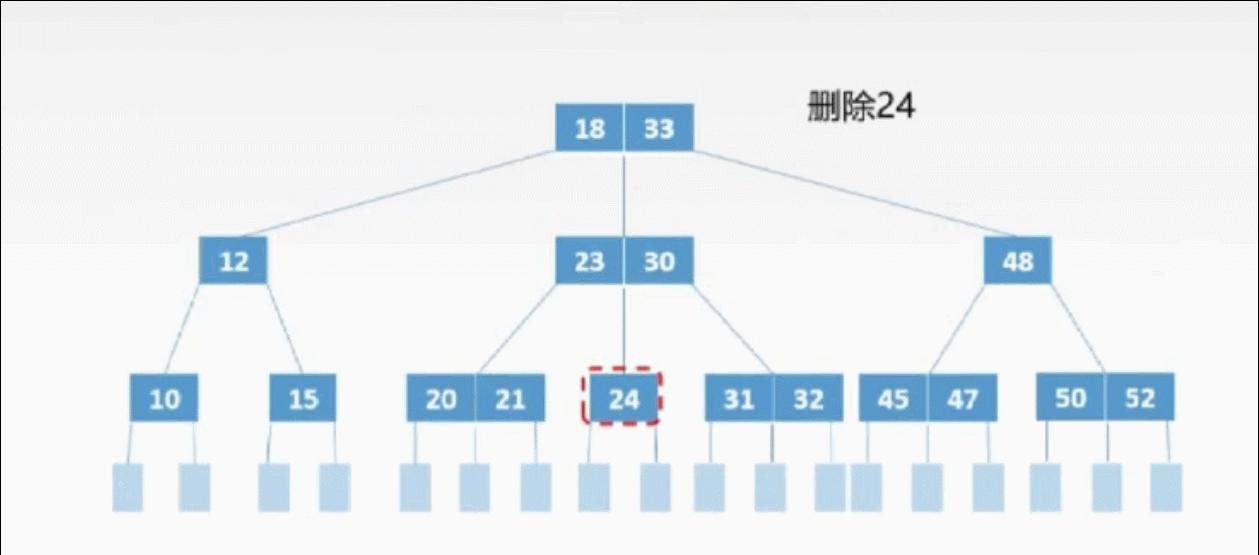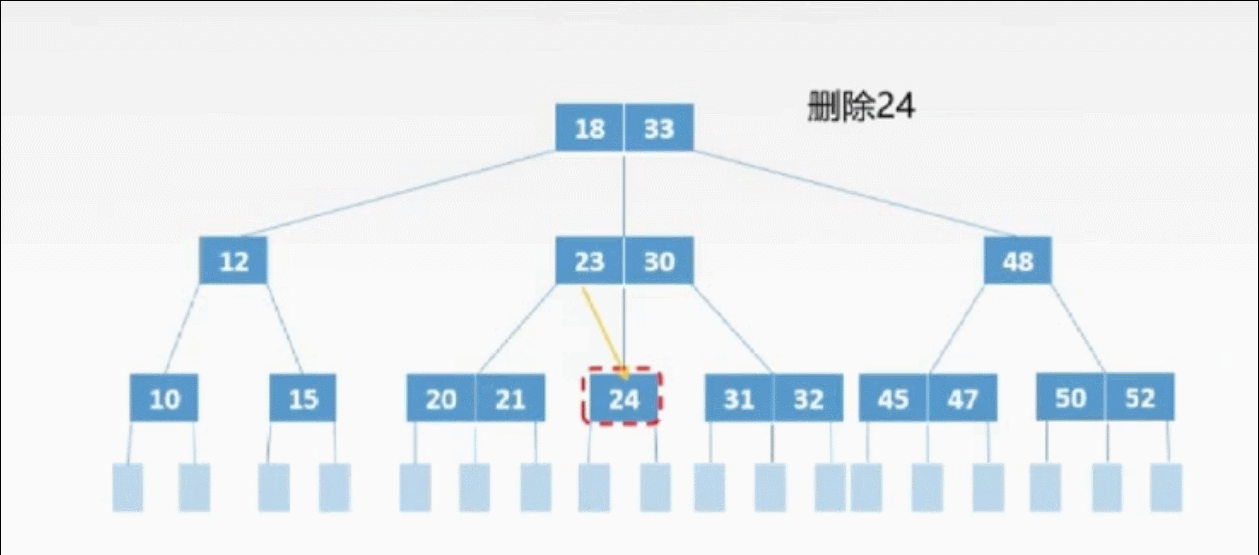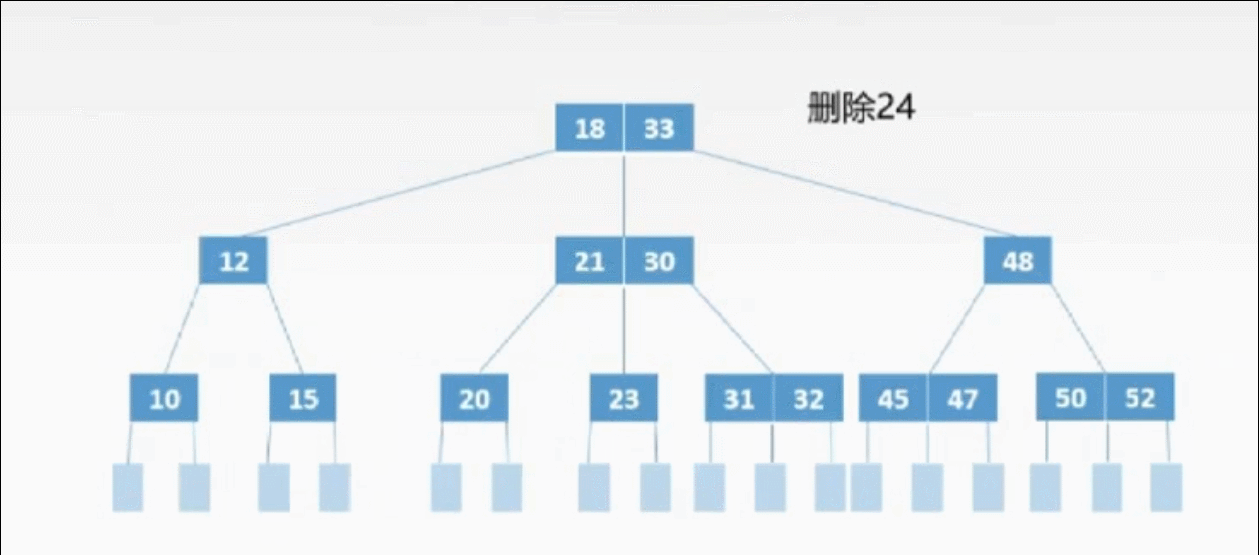
三、删除
①终端上的3种删除情况：
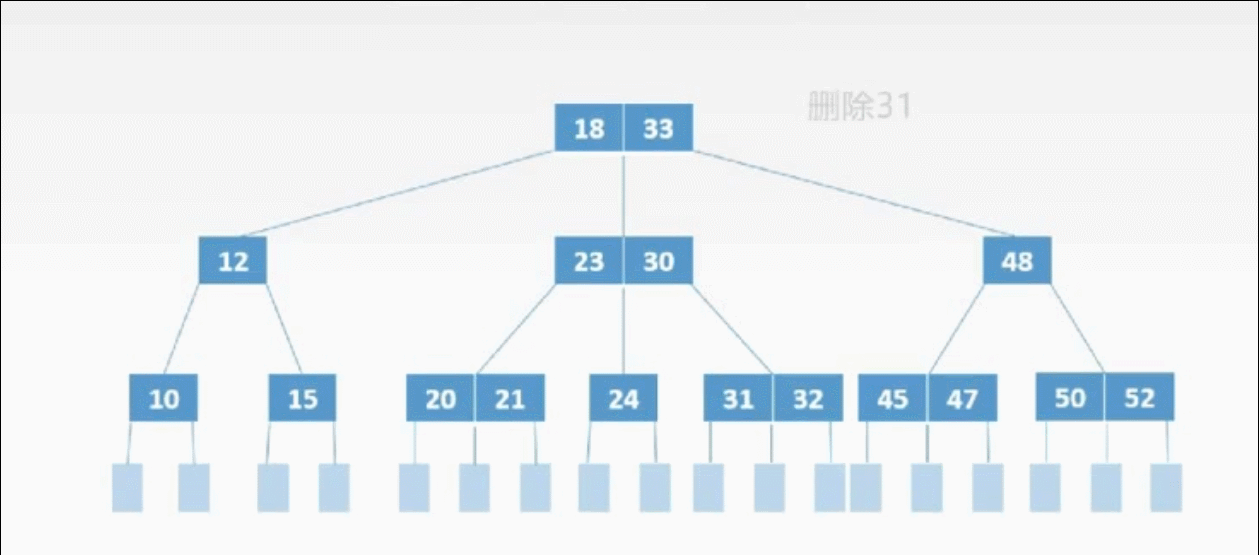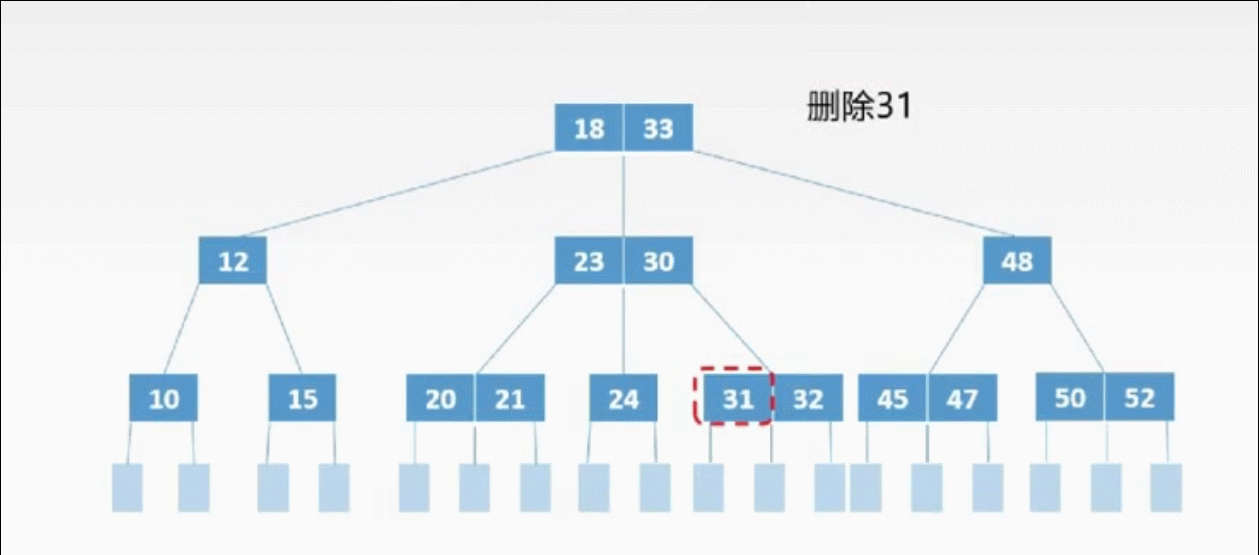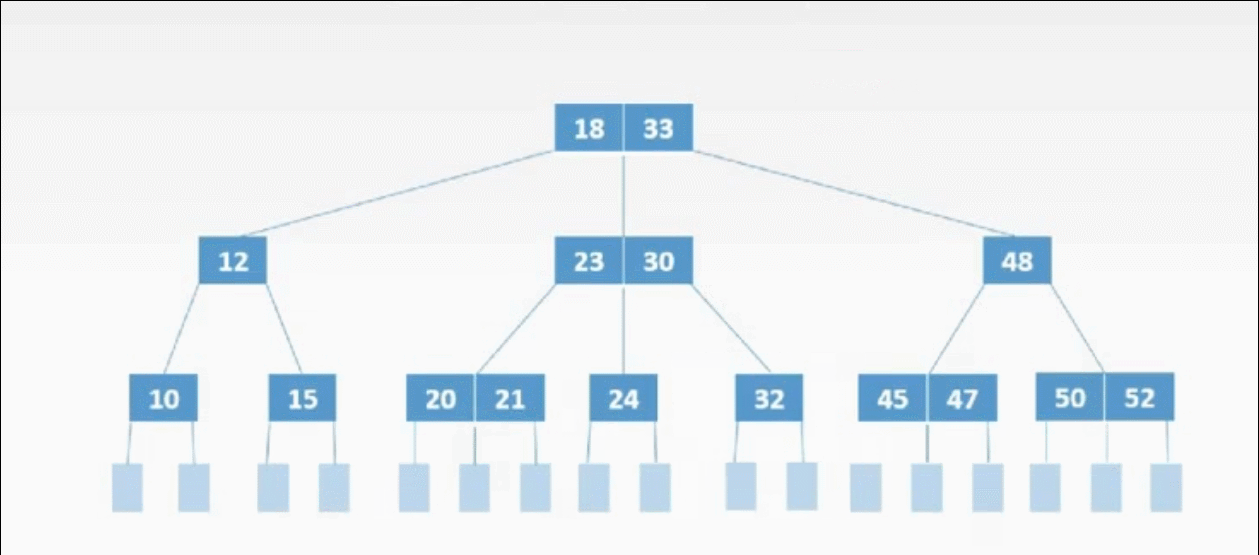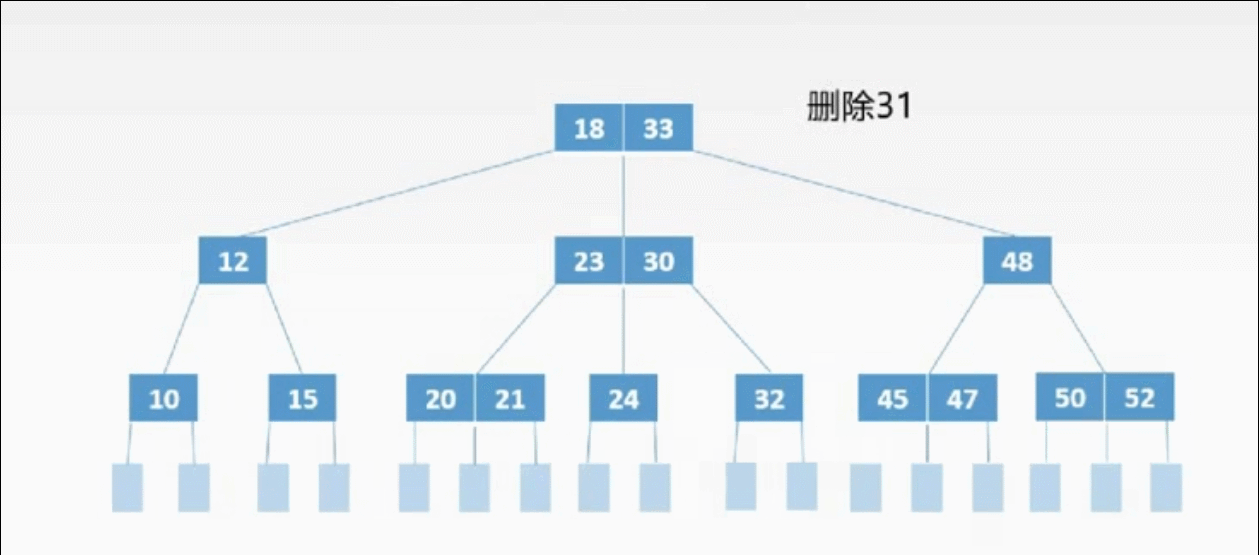
B树删除从左兄弟结点借一个
B树删除从右兄弟结点借一个
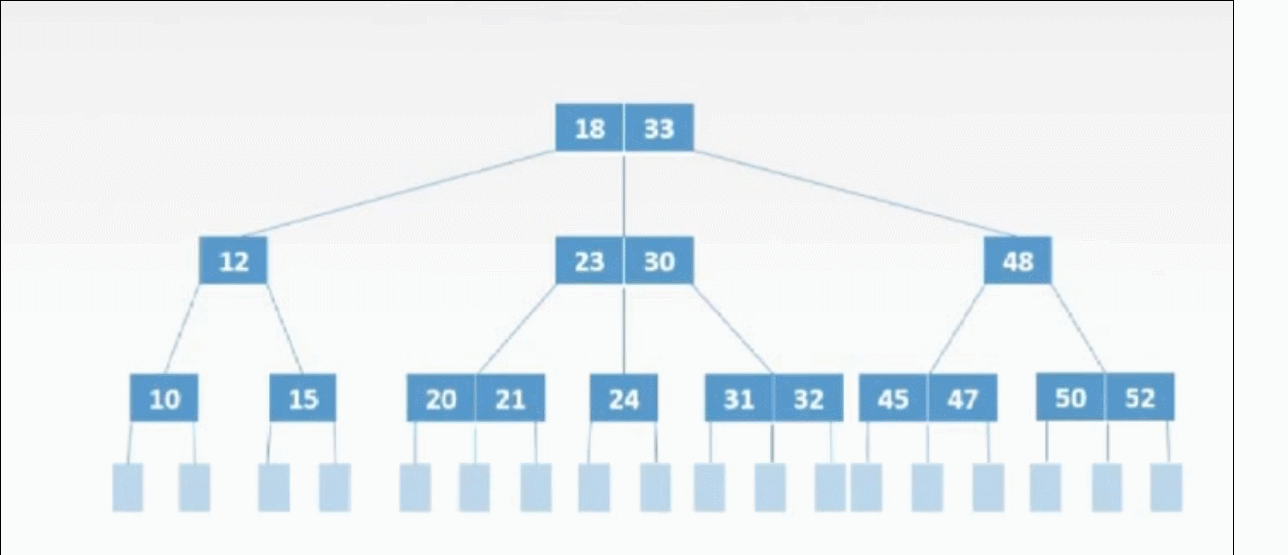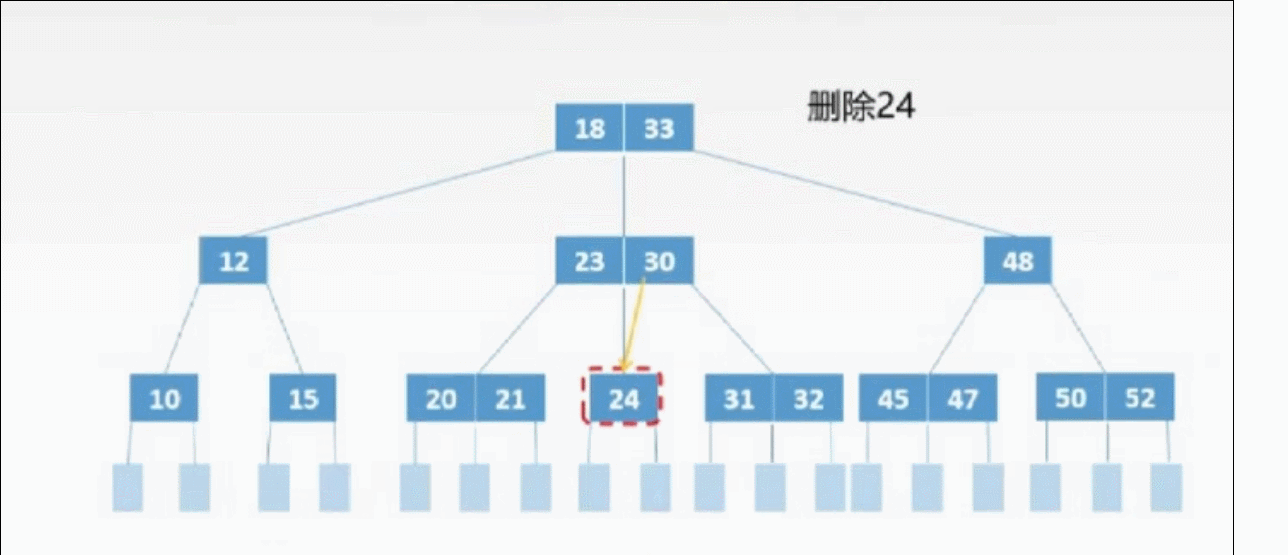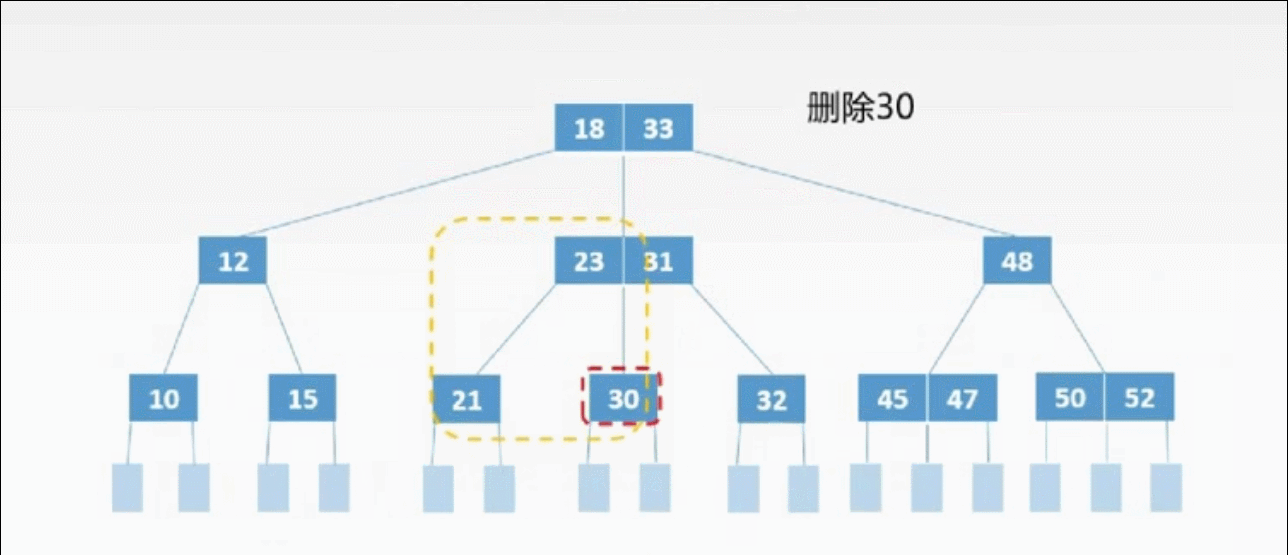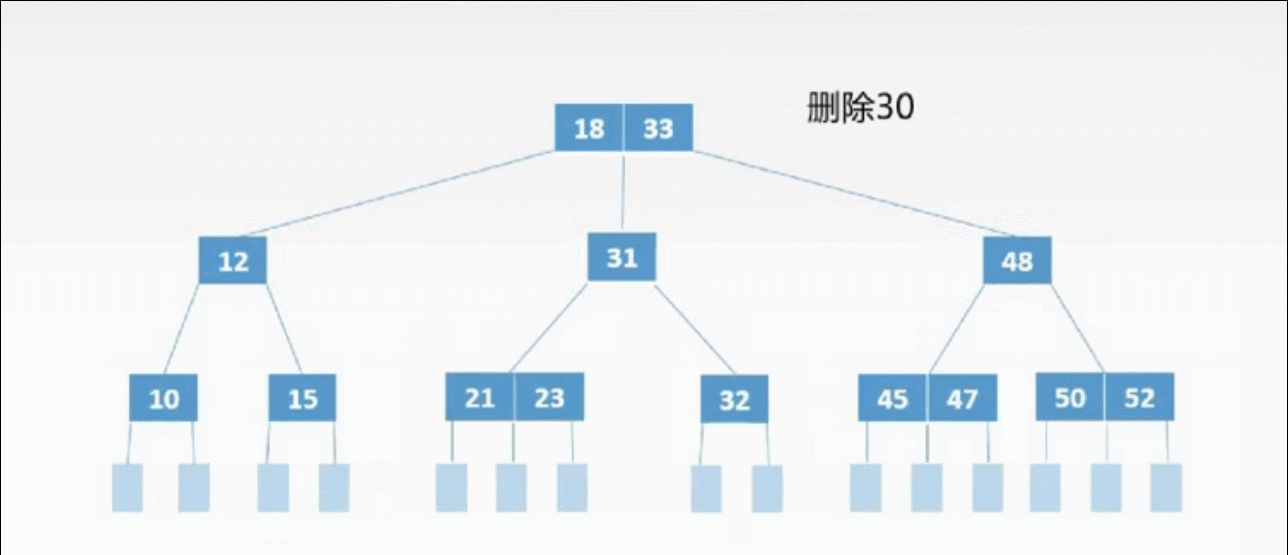
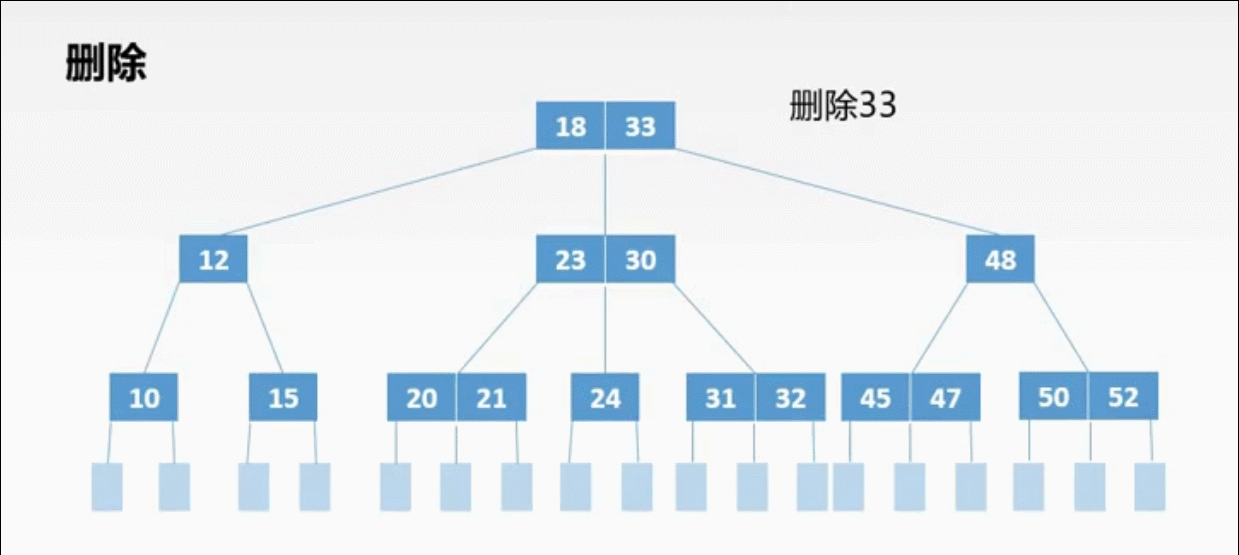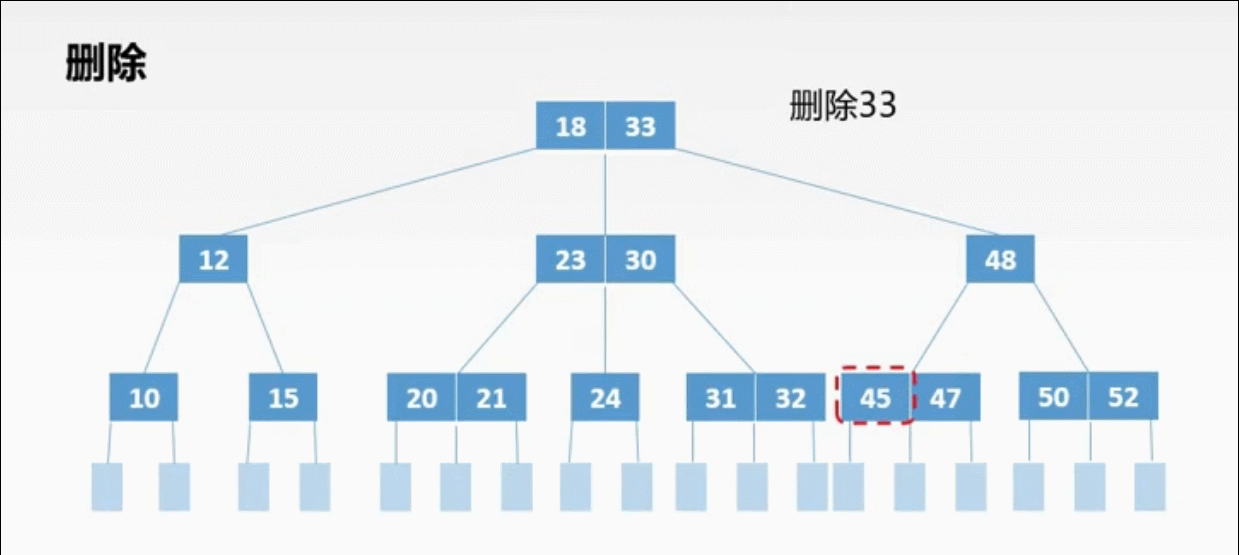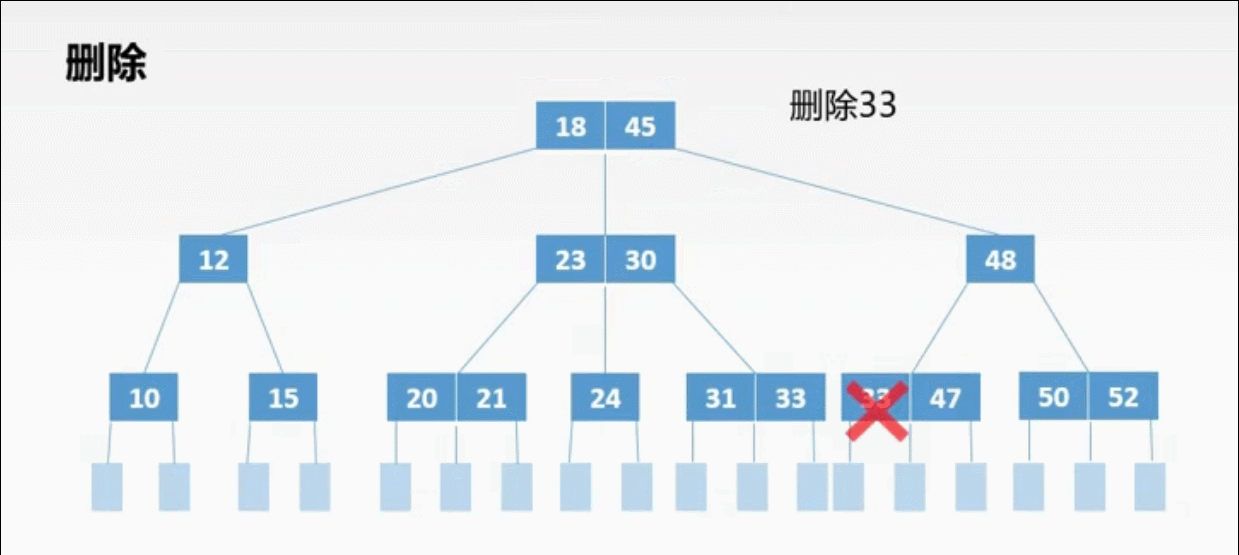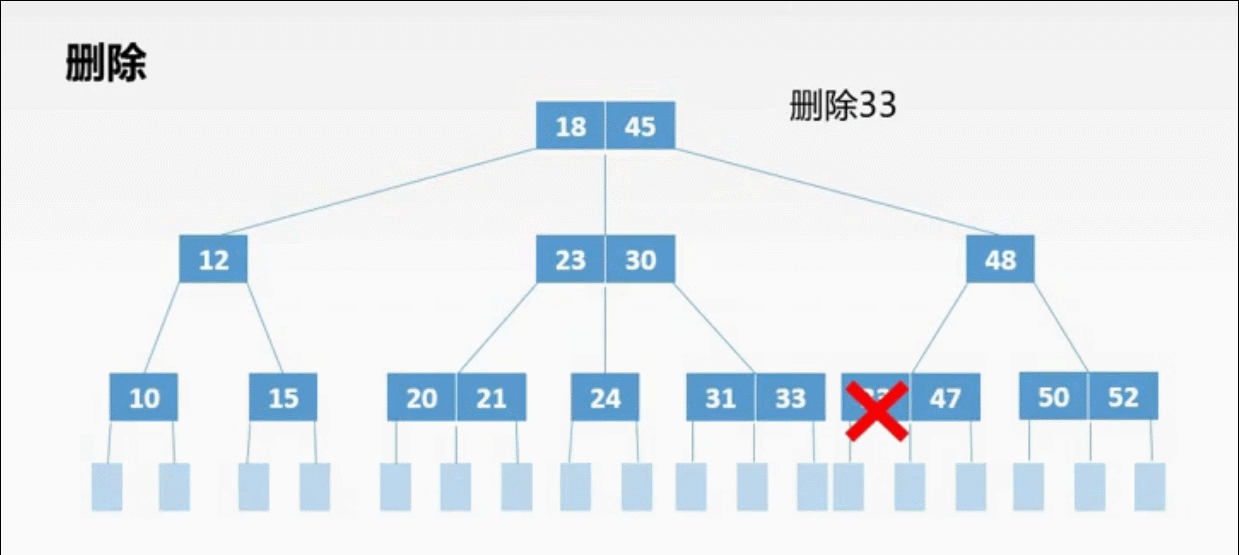
②非终端上的3种删除情况：
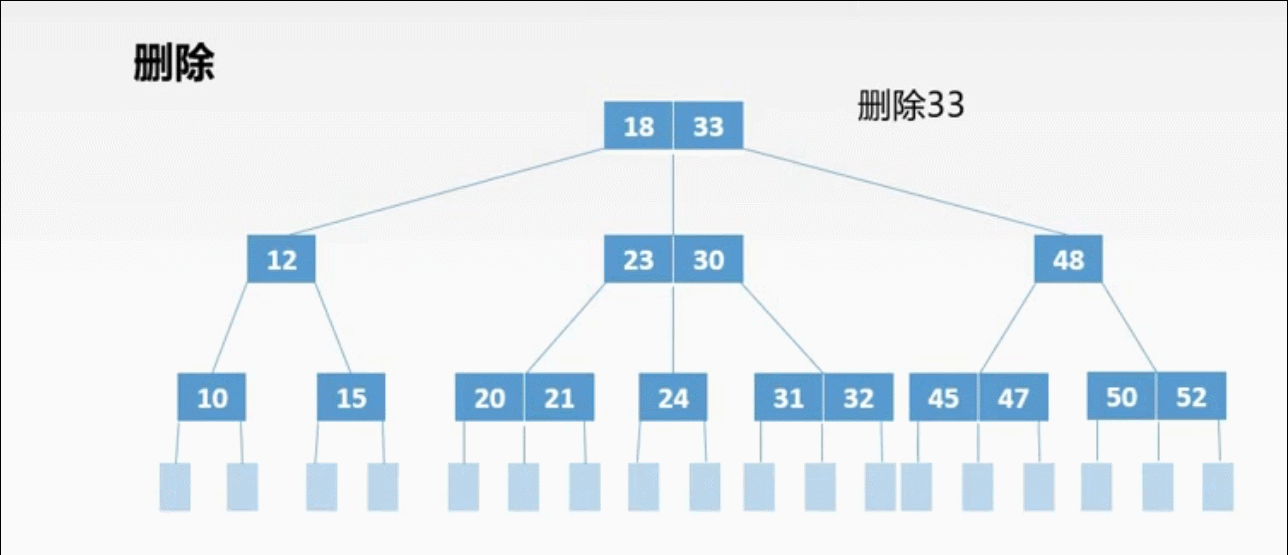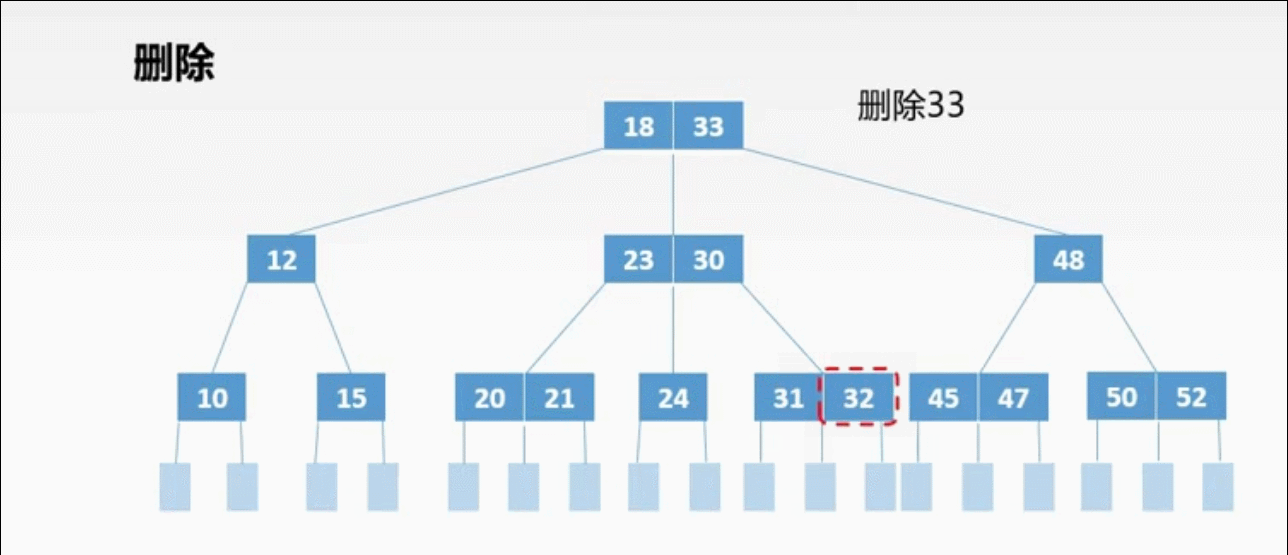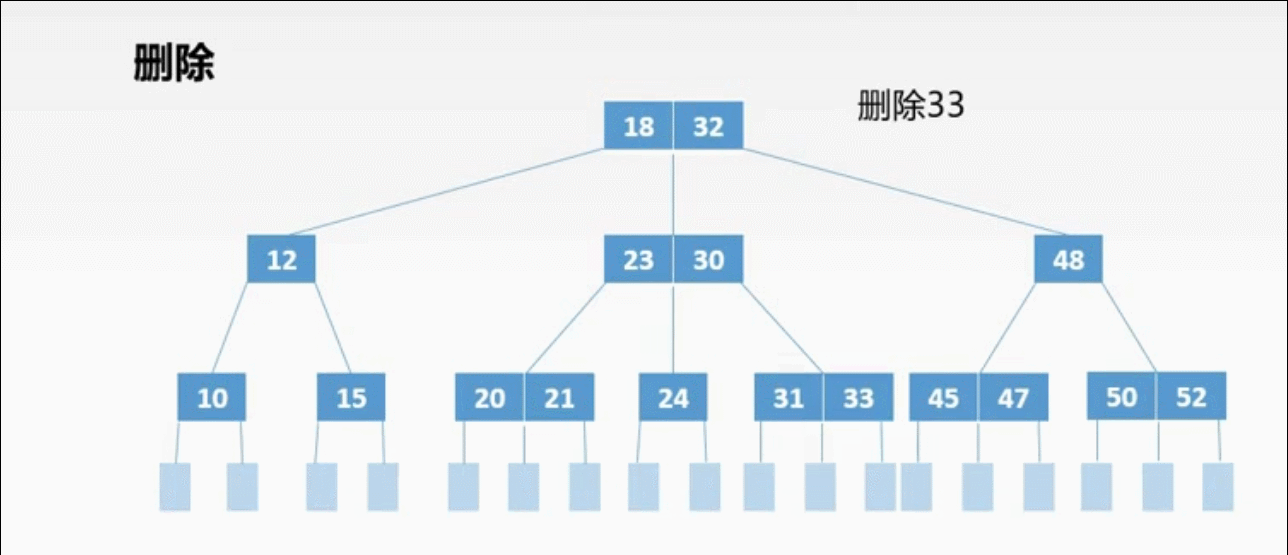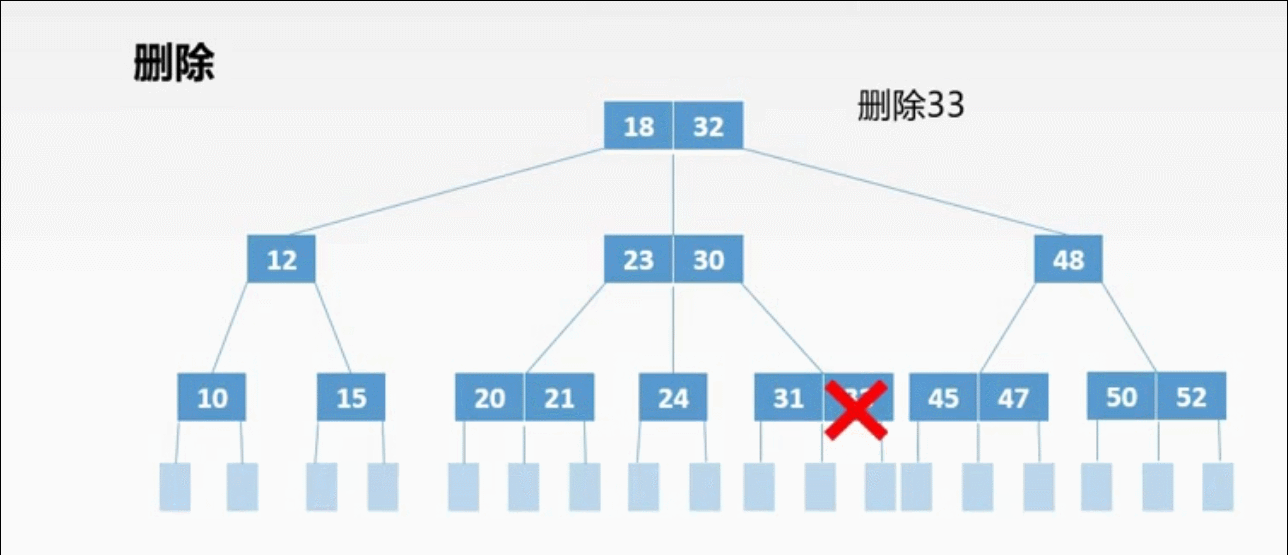
非终端上的删除操作转化为终端上的删除操作
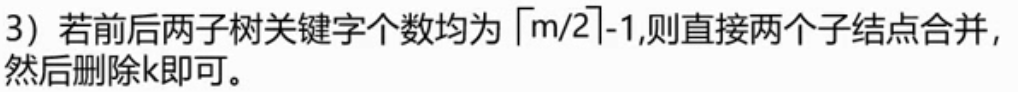
B+树
B+树
---截图来源于《王道数据结构》CSKAOYAN.COM
坚持就是胜利，坚持定会成功！
