LC 417太*洋大西洋水流问题

LC 417 太*洋大西洋水流问题

题目描述

有一个 m × n 的矩形岛屿，与 太*洋 和 大西洋 相邻。 “太*洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海*面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附*的任何单元格流入海洋。

返回 网格坐标 result 的 2D列表 ，其中 result[i] = [ri, ci] 表示雨水可以从单元格 (ri, ci) 流向 太*洋和大西洋 。

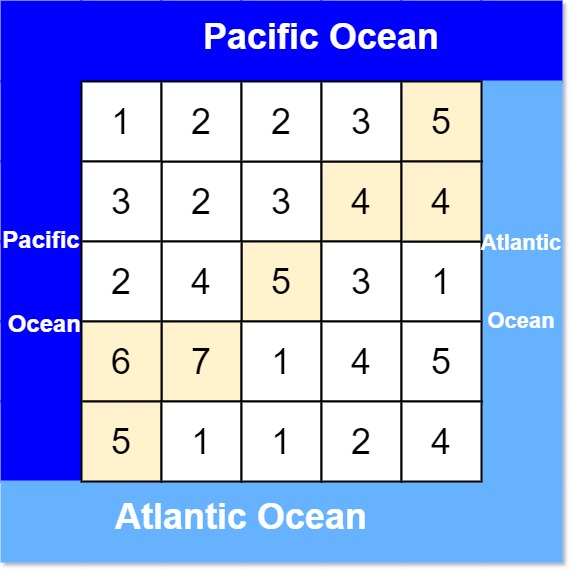
示例1：

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

题意：

给定我们这样一个二维矩阵，矩阵中的每个元素代表水流高度， 这道题要求我们求出矩阵中哪些点能既流到大西洋又流到太*洋，返回一个这些点组成的vector。

做法

我们可以观察示例1的图片，图中左边和上边的一列和一行靠*太*洋；右边和下边的一列和一行靠*大西洋，我们可以发现要我们的事既可以流向大西洋又可以流向太*洋的点。我们如果每个点都搜索的话可能会超时，但是我们可以考虑反向搜索；从太*洋的边界左边和上边开始搜，搜到后标记一下，然后从大西洋的边界右边和上边开始搜，搜到后标记一下，然后大西洋和太*洋搜到的交集就是我们的答案，如下图所示：

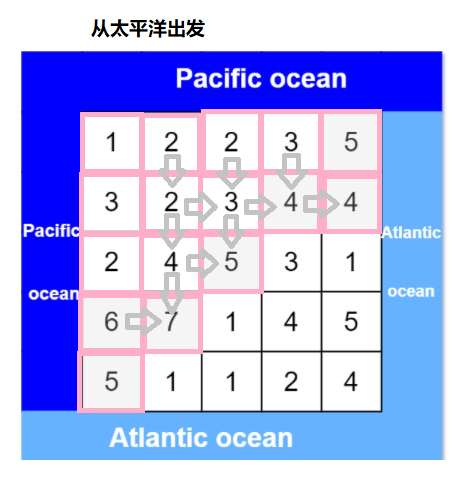
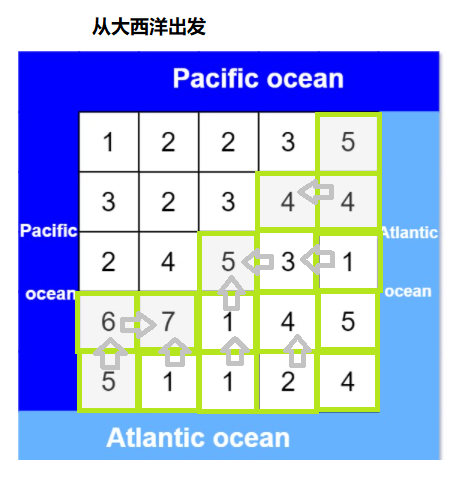
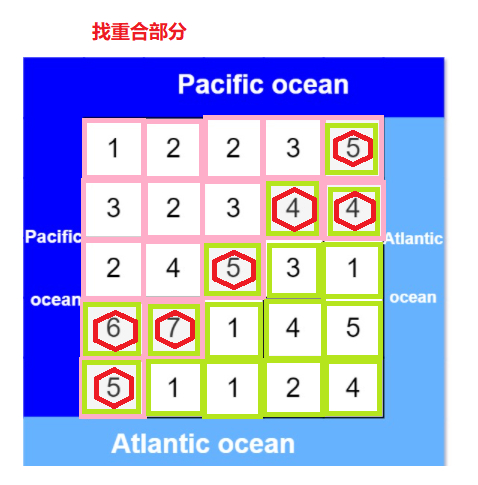
DFS O(nm)

class Solution {
public:
    int n, m;
    vector<vector<int>> res;
    vector<vector<int>> h;
    int dir[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
    int vis[205][205];
    // st为1表示太*洋， st为2表示大西洋，两个都访问了即是1 + 2 = 3，这里考虑用位运算进行标记
    void dfs(int x, int y, int st)
    {
        if (vis[x][y] & st) return;
        vis[x][y] |= st;

        for (int i = 0; i < 4; i ++)
        {
            int nx = x + dir[i][0], ny = y + dir[i][1];
            if (nx >= 0 && nx < n && ny >= 0 && ny < m && h[nx][ny] >= h[x][y])
            {
                dfs(nx, ny, st);
            }
        }
    }

    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        n = heights.size(), m = heights[0].size();
        h = heights;
        for (int i = 0; i < n; i ++)
        {
            dfs(i, 0, 1);
            dfs(i, m - 1, 2);
        }
        for (int j = 0; j < m; j ++)
        {
            dfs(0, j, 1);
            dfs(n - 1, j, 2);
        }
        for (int i = 0; i < n; i ++)
        {
            for (int j = 0; j < m; j ++)
            {
                if (vis[i][j] == 3)
                {
                    res.push_back({i, j});
                }
            }
        }
        return res;
    }
};

BFS O(nm)

class Solution {
public:
    typedef pair<int, int> PII;
    int n, m;
    vector<vector<int>> res;
    vector<vector<int>> h;
    int dir[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
    int vis[205][205];

    void dfs(int x, int y, int st)
    {
        if (vis[x][y] & st) return;
        vis[x][y] |= st;

        for (int i = 0; i < 4; i ++)
        {
            int nx = x + dir[i][0], ny = y + dir[i][1];
            if (nx >= 0 && nx < n && ny >= 0 && ny < m && h[nx][ny] >= h[x][y])
            {
                dfs(nx, ny, st);
            }
        }
    }

    void bfs(int x, int y, int st)
    {
        queue<PII> q;
        q.push({x, y});
        vis[x][y] |= st;
        while (q.size())
        {
            auto t = q.front();
            int tx = t.first, ty = t.second;
            q.pop();
            for (int i = 0; i < 4; i ++)
            {
                int nx = tx + dir[i][0], ny = ty + dir[i][1];
                if (nx >= 0 && nx < n && ny >= 0 && ny < m && h[nx][ny] >= h[tx][ty] && !(vis[nx][ny] & st))
                {
                    vis[nx][ny] |= st;
                    q.push({nx, ny});
                }
            }
        }
    }

    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        n = heights.size(), m = heights[0].size();
        h = heights;
        for (int i = 0; i < n; i ++)
        {
            bfs(i, 0, 1);
            bfs(i, m - 1, 2);
        }
        for (int j = 0; j < m; j ++)
        {
            bfs(0, j, 1);
            bfs(n - 1, j, 2);
        }
        for (int i = 0; i < n; i ++)
        {
            for (int j = 0; j < m; j ++)
            {
                if (vis[i][j] == 3)
                {
                    res.push_back({i, j});
                }
            }
        }
        return res;
    }
};