Algorithm Template

数据范围推算法

Sort排序动画

quick_sort

Step:

  • 第一步，选择一个基准数x，可以选当前数组的最后一个元素，第一个元素或者数组中间元素
  • 第二步，双指针扫描（调整区间），设定i指向当前排序区间的左端点 - 1，设定j指向当前排序区间的右端点 + 1， 如果 i < j那么执行循环，首先左边i指针指向元素如果小于基准数则i指针右移，找到第一个i < j && a[i] >= x的数；其次右边j指针指向元素如果大于基准数则j指针左移，找到第一个i < j && a[j] >= x的数；如果此时i < j, 则将i指针指向的值和j指针指向的值交换；
  • 第二步会将小于x的数乱序排到x的左边，将大于x的数乱序排到x的右边，即完成一趟排序，接下来要做的是递归的排序x的左边和x的右边区间即可
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
int a[N];

void quick_sort1(int l, int r);
void quick_sort2(int l, int r);

int main(void)
{
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &a[i]);
	}
	quick_sort2(0, n - 1);

	for (int i = 0; i < n; i ++)
	{
		printf("%d ", a[i]);
	}

	return 0;
}

// do-while version
void quick_sort1(int l, int r)
{
	if (l >= r)
	{
		return ;
	}
	int mid = (l + r) >> 1;
	int x = a[mid];
	int i = l - 1, j = r + 1;
	while (i < j)
	{
		do
		{
			i ++;
		} 
		while (a[i] < x);

		do
		{
			j --;
		}
		while (a[j] > x);
		if (i < j)
		{
			swap(a[i], a[j]);
		}
	}
	quick_sort1(l, j);
	quick_sort1(j + 1, r);
}


// while version
void quick_sort2(int l, int r)
{
	if (l >= r)
	{
		return ;
	}
	int mid = (l + r) >> 1;
	int x = a[mid];
	int i = l - 1, j = r + 1;
	while (i < j)
	{
		while (a[++i] < x)
		{
		  
		}


		while (a[--j] > x) 
		{
		  
		}

		if (i < j)
		{
			swap(a[i], a[j]);
		}
	}
	quick_sort2(l, j);
	quick_sort2(j + 1, r);
}

第K个数（TopK问题）

题意：求数组中第K个小或第K个大的数是多少, 或者求前K个小或前K个大的数

  • 解法1： Sort一遍，返回数组第k个元素即可O(nlogn) 
    • #include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

int a[N];

int main(void)
{
	int n, k;
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &a[i]);
	}
	sort(a, a + n);
	printf("%d\n", a[k - 1]);
	return 0;
}
  • 解法2：快排分治 O(N)
    • 首先考虑快排的思想，对于第K小的数来看，快排每次选择一个基准x，将比基准x小的数排到左边，将比基准x大的数排到右边，而一趟下来我们就知道<=x的元素个数有numLeft个，而此时我们可以比较k与numLeft的个数，如果k < numleft, 则我们就在区间的左边找第K小的数；反之在区间的右边找第k - numLeft小的数即可
    • 对于前K小的数来看，一样依照上面的思路只不过每次我们需要返回的是一个范围的数
    • #include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

int a[N];
vector<int> arr;
priority_queue<int> q; // 大根堆

int _knum(int l, int r, int k);
vector<int> _knums(vector<int>& arr, int l, int r, int k);
vector<int> _knums1(vector<int>& arr, int k);

int main(void)
{
	int n, k, input;
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &input);
		// scanf("%d", &a[i]);
		arr.push_back(input);
	}
	// int res = _knum(0, n - 1, k);
	// printf("%d\n", res);
	vector<int> res = _knums(arr, 0, arr.size() - 1, k);
	for (auto &i: res)
	{
		printf("%d ", i);
	}
	return 0;
}

// 求单个第K小方案
int _knum(int l, int r, int k)
{
	if (l >= r) return a[l];
	int x = a[(l + r) >> 1];
	int i = l - 1, j = r + 1;
	while (i < j)
	{
		do
		{
			i ++;
		}
		while (a[i] < x);

		do
		{
			j --;
		}
		while (a[j] > x);
		if (i < j)
		{
			swap(a[i], a[j]);
		}
	}
	int numLeft = j - l + 1;
	if (k <= numLeft)
	{
		return _knum(l, j, k);
	}
   	else 
	{
		return _knum(j + 1, r, k - numLeft);
	}
}

vector<int> _knums(vector<int>& arr, int l, int r, int k)
{
	int x = arr[l];
	int i = l, j = r;
	while (i < j)
	{
		while (i < j && arr[j] >= x) j --;
		while (i < j && arr[i] <= x) i ++;

		swap(arr[i], arr[j]);
	}
	swap(arr[i], arr[l]);
	if (i > k)
	{
		return _knums(arr, l, i - 1, k);
	}
	if (i < k) 
	{
		return _knums(arr, i + 1, r, k);
	}

	vector<int> tmp;
	tmp.assign(arr.begin(), arr.begin() + k);
	return tmp;
}

vector<int> _knums1(vector<int>& arr, int k) 
{
	for (auto &i : arr)
	{
		if (q.size() < k)
		{
			q.push(i);
		} 
		else if (q.top() > i)
		{
			q.pop();
			q.push(i);
		}
	}
	vector<int> tmp;
	while (!q.empty())
	{
		tmp.push_back(q.top());
		q.pop();
	}
	return tmp;
}
  • 解法3：优先队列（堆）,O(NlogK)
    • 如果求第K个数，用小根堆存储元素，然后在pop出来n - k个元素
    • 如果求前K个数，比如前K小，用大根堆存储一个容量为K的堆，每次pop出最大的数，堆中保留的就是前K小个数；前K大反向操作即可；
    • #include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

priority_queue<int> q;

int main(void)
{
	int n, k, x;
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &x);
		q.push(x);
	}
	while (n > k)
	{
		q.pop();
	}
	printf("%d\n", q.top());
	return 0;
}
  • 解法4：平衡二叉搜索树（红黑树O(NlogK)) Set 
    • 
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;

// priority_queue<int> q;
multiset<int> S;

int main(void)
{
	int n, k, x;
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &x);
		S.insert(x);
	}
	int res = 0;
	for (auto t: S)
	{
	    k --;
	    if (k == 0)
	    {
	        res = t;
	    }
	}
	printf("%d\n", res);
	return 0;
}
    • 解法5： 桶排序（数组内元素范围不大的情况下）O(n)

归并排序

  • 确定分界点
  • 递归左右区间
  • 合并子问题
  • void merge_sort(int l, int r)
{
	if (l >= r) // 递归出口
	{
		return ;
	}
	int mid = (l + r) >> 1; // 确定分界点
	merge_sort(l, mid); // 划分左区间
	merge_sort(mid + 1, r); // 划分右区间
	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
	{
		if (a[i] < a[j]) 
		{
			tmp[k] = a[i];
			k ++;
			i ++;
		}
		else 
		{
			tmp[k] = a[j];
			k ++;
			j ++;
		}
	}
	while (i <= mid) // 还剩下元素没有加入tmp中
	{
		tmp[k] = a[i];
		k ++;
		i ++;
	}
	while (j <= r)
	{
		tmp[k] = a[j];
		k ++;
		j ++;
	}
	for(i = l, j = 0; i <= r; i ++, j ++)
	{
		a[i] = tmp[j];
	}
}

求解数组中的逆序数

  • 逆序对的定义如下：对于数列的第 i个和第 j个元素，如果满足 i<j且 a[i]>a[j]，则其为一个逆序对；否则不是。
  • 归并排序求逆序数O(nlogn)
    • 在归并排序中的第三步我们去遍历左区间和右区间时会比较左区间中第i个元素与右区间的第j个元素，它们的相对位置属于i < j, 如果此时满足a[i] > a[j], 则满足逆序数的定义， 并且针对于当前j，有 mid -i + 1个元素会与当前j成为逆序数。 why ？ 因为针对于左区间[i, mid]和右区间[mid + 1, r], 在经历划分合并时已经有序， 左区间和右区间都是单调递增，所以针对于i < j && a[i] > a[j]时，[i, mid]之间的所有元素都和当前j是逆序数。
    • #include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int a[N], tmp[N]; // tmp数组辅助记录
long long res = 0;

void merge_sort(int l, int r);

int main(void)
{
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &a[i]);
	}
	merge_sort(0, n - 1);
	// for (int i = 0; i < n; i ++)
	// {
	// 	printf("%d ", a[i]);
	// }
	printf("%lld\n", res);
	return 0;
}

void merge_sort(int l, int r)
{
	if (l >= r) // 递归出口
	{
		return ;
	}
	int mid = (l + r) >> 1; // 确定分界点
	merge_sort(l, mid); // 划分左区间
	merge_sort(mid + 1, r); // 划分右区间
	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
	{
		if (a[i] <= a[j]) 
		{
			tmp[k] = a[i];
			k ++;
			i ++;
		}
		else 
		{
			tmp[k] = a[j];
			k ++;
			j ++;
			res += mid - i + 1;
		}
	}
	while (i <= mid) // 还剩下元素没有加入tmp中
	{
		tmp[k] = a[i];
		k ++;
		i ++;
	}
	while (j <= r)
	{
		tmp[k] = a[j];
		k ++;
		j ++;
	}
	for(i = l, j = 0; i <= r; i ++, j ++)
	{
		a[i] = tmp[j];
	}
}
  • 树状数组（待更）

二分模板

  • lower_bound()，查找第一个>=x的元素的位置

    • int l = 0, r = n - 1;
while (l < r)
{
    int mid = (l + r) >> 1;
    if (a[mid] < x)
    {
        l = mid + 1;
    }
    else 
    {
        r = mid;
    }
}
    • 当a[mid]小于x时，令l = mid + 1，mid及其左边的位置被排除了，可能出现解的位置是mid + 1及其后面的位置；当a[mid] >= x时，说明mid及其左边可能含有值为x的元素；当查找结束时，l与r相遇，l所在元素若是x则一定是x出现最小位置，因为l左边的元素必然都小于x。

  • upper_bound(), 查找最后一个<=x的元素的位置

    • int l = 0, r = n;
while (l + 1 < r)
{
    int mid = l + r >> 1;
    if (a[mid] <= x)
    {
        l = mid;
    }
    else 
    {
        r = mid;
    }

}
    • 当a[mid] <= x时，待查找元素只可能在mid及其后面，所以l = mid；当a[mid] > x时，待查找元素只会在mid左边，令r = mid。为什么不令r = mid - 1呢？因为如果按照上一个二分的写法，循环判断条件还是l < r,当只有两个元素比如2 2时，l指向第一个元素，r指向第二个元素，mid指向第一个元素，a[mid] <= x，l = mid还是指向第一个元素，指针不移动了，陷入死循环了，此刻l + 1 == r，未能退出循环。那么直接把循环判断条件改成l + 1 < r呢？此时一旦只有两个元素，l和r差1，循环便不再执行，查找错误。所以这里出现了二分的典型错误，l == r作为循环终止条件，会出现死循环，l + 1 == r作为循环终止条件，会出现查找错误。
  • #include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int lower_binary_search(int a[], int l, int r, int x);
int upper_binary_search(int a[], int l, int r, int x);

int a[N];

int main(void)
{
	int n, q, k;
	scanf("%d%d", &n, &q);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &a[i]);
	}
	while (q --)
	{
		scanf("%d", &k);
		int left = lower_binary_search(a, 0, n - 1, k);
		if (left == - 1)
		{
			printf("-1 -1\n");
			continue;
		}
		int right = upper_binary_search(a, 0, n, k);
		printf("%d %d\n", left, right);
	}
	return 0;
}

int lower_binary_search(int a[], int l, int r, int x)
{
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (a[mid] < x)
		{
			l = mid + 1;
		}
		else 
		{
			r = mid;
		}

	}
	if (a[l] == x)
	{
		return l;
	}
	return -1;
}

int upper_binary_search(int a[], int l, int r, int x)
{
	while (l + 1 < r)
	{
		int mid = (l + r) >> 1;
		if (a[mid] <= x)
		{
			l = mid;
		}
		else 
		{
			r = mid;
		}
	}
	if (a[l] == x)
	{
		return l;
	}
	return -1;
}

浮点数二分

  • 数的三次方根， desc：给定一个浮点数n求它的三次方根

    • 二分(logn): 从 答案范围-10000.0 ~ 10000.0开始二分，找到二分后的数的三次方即可， 而终止条件应该为r - l >= eps(浮点数的一个常数值)
    • #include <bits/stdc++.h>

using namespace std;

const double eps = 1e-7;

int main(void)
{
	double n;
	scanf("%lf", &n);
	double l = -10000.0, r = 10000.0;
	while (r - l >= eps)
	{
		double mid = (l + r) / 2.0;
		if (mid * mid * mid <= n)
		{
			l = mid;
		}
		else 
		{
			r = mid;
		}
	}
	printf("%.6lf\n", l);
	return 0;
}

  • 剑指Offer72， 求平方根

    • 给定一个非负整数 x ，计算并返回 x 的平方根，即实现 int sqrt(int x) 函数。正数的平方根有两个，只输出其中的正数平方根。如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。
    • 传送门
    • 数据范围是\(0\) ~ \(2^{31} - 1\) ， 我们可以去二分答案，二分范围是0 ~ x, 用模板二upper_binary_search即可，注意要开long long!!!, 因为二分的答案的平方和x去比较，不开long long 会wa掉
    • class Solution {
public:
    typedef long long LL;
    int mySqrt(int x) {
        if (x <= 1) return x;
        LL l = 0, r = x;
        while (l + 1 < r)
        {
            LL mid = (l + r) >> 1;
            if (mid * mid <= x)
            {
                l = mid;
            }
            else 
            {
                r = mid;
            }
        }
        return (int)l;
    }
};

前缀和

  • 一维前缀和
    • 首先做一个预处理，定义一个sum[]数组，sum[i]代表a数组中前i个数的和。
    • 求区间[l, r]的区间和，可以被计算为sum[r] - sum[l - 1]
    • #include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
int a[N], sum[N];

int main(void)
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; i ++)
	{
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= n; i ++)
	{
		sum[i] = sum[i - 1] + a[i - 1];
	}
	int l, r;
	while (m --)
	{
		scanf("%d%d", &l, &r);
		printf("%d\n", sum[r] - sum[l - 1]);
	}
	return 0;
}
  • 二维前缀和
    • 二维前缀和即为以左上角为起点右下角为终点的这一块矩形区域。
    • 二维前缀和 sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + a[i - 1][j - 1] - sum[i - 1][j- 1]
    • 求区间[x1, y1]为左上角， 区间[x2, y2]为右下角的矩阵和可以等价于sum[x2][y2] - sum[x1 - 1, y2] - sum[x2, y1 - 1] + sun[x1 - 1, y1 - 1]
    • #include <bits/stdc++.h>

using namespace std;

const int MAXN = 1005;

typedef long long LL;

LL a[MAXN][MAXN], sum[MAXN][MAXN];

int main(void)
{
	int n, m, q, x1, x2, y1, y2;
	scanf("%d%d%d", &n, &m, &q);
	for (int i = 0; i < n; i ++)
	{
		for(int j = 0; j < m; j ++)
		{
			scanf("%lld", &a[i][j]);
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			sum[i][j] = sum[i][j - 1] + sum[i - 1][j] + a[i - 1][j - 1] - sum[i - 1][j - 1]; 
		}
	}

	while (q --)
	{
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		printf("%lld\n", sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]);
	}
	return 0;
}

差分

  • 一维差分

    • 对询问q次， 每次区间[l, r]加上c， 求q次询问后，整个数组的值

    • 差分定义：

      • 首先给定一个原数组a：a[1], a[2], a[3]...a[n];
      • 然后我们构造一个数组b ： b[1] ,b[2] , b[3]...b[i];
      • 使得 a[i] = b[1] + b[2]+ b[3] +... + b[i]
      • 也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
      • 构造差分最为直接的方法为b[n] = a[n] - a[n - 1]
      • 差分数组b的前缀和为a数组本身

    • 如果我们构造好差分数组，每次区间[l, r]加上c, 我们可以视为对查分数组b[l] += c， 对b[r + 1] -= c我们对[l,r]的区间的差分都加上c等同于在原数组该区间都加上c,我们假定对左端点l加上c，那么l之前的所有数和l的差分都会比之前多c，而如果对r + 1端点减去c代表r+1之后的所有数比端点r多c， 即等同于对区间[l, r]加上c.

    • #include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int a[N], diff[N], ans[N];

int main()
{
	int n, m, l, r, c;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++)
	{
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= n; i ++)
	{
		diff[i] = a[i] - a[i - 1];
	}
	while (m --)
	{
		scanf("%d%d%d", &l, &r, &c);
		diff[l] += c;
		diff[r + 1] -= c;
	}
	for (int i = 1; i <= n; i ++)
	{
		ans[i] = ans[i - 1] + diff[i];
	}
	for (int i = 1; i <= n; i ++)
	{
		printf("%d ", ans[i]);
	}
	return 0;
}
  • 二维差分矩阵
    • a数组是原数组diff数组是a数组的差分数组， 而a数组也是diff数组的前缀和数组， 构造差分数组diff使得a数组中a[i][j]是diff数组左上角[1, 1]到右下角[i, j]所包围矩形元素的和。
    • a数组是diff数组的前缀和数组，比如对diff数组的diffi][j]的修改，会影响到a数组中从a[i][j]及其往后的每一个数。
    • #include <bits/stdc++.h>

using namespace std;

const int N = 1005;

int a[N][N], diff[N][N];

void insert(int x1, int y1, int x2, int y2, int c);

int main()
{
	int n, m, q, x1, y1, x2, y2, c;
	scanf("%d%d%d", &n, &m, &q);
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			scanf("%d", &a[i][j]);
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			insert(i, j, i, j, a[i][j]);
		}
	}
	while (q --)
	{
		scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
		insert(x1, y1, x2, y2, c);
	}
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			printf("%d ", diff[i][j]);
		}
		puts("");
	}
	return 0;
}

void insert(int x1, int y1, int x2, int y2, int c)
{
	diff[x1][y1] += c;
	diff[x2 + 1][y1] -= c;
	diff[x1][y2 + 1] -= c;
	diff[x2 + 1][y2 + 1] += c;
}

数组模拟单链表

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

// e: 存储链表的value
// ne：存储链表的节点， ne[i] = idx, 第i个节点的下一个节点编号为idx
// head：头节点
// idx：当前节点编号
int e[N], ne[N], head, idx;

void initLinkNode()
{
	head = -1;
	idx = 0;
}

void insertHead(int x)
{
	e[idx] = x;
	ne[idx] = head;
	head = idx ++;
}

void deleteNode(int k)
{
	ne[k] = ne[ne[k]];
}

void insertNode(int k, int x)
{
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx ++;
}

void traverse(int head)
{
	for (int i = head; i != -1; i = ne[i])
	{
		printf("%d->", e[i]);
	}
}

计算中缀表达式

  • 判断字符是否为数字，若是数字则继续判断下一位是否为数字计算是几位数字然后存入num栈中
  • 判断左括号，如果是则push到操作栈
  • 判断右括号，一直计算直至遇到左括号
  • 如果为其他运算符，判断当前元素与操作符栈顶元素的优先级，如果栈顶元素优先级高则优先计算栈顶元素运算符，再入栈
  • 最后如果操作符栈不为空，则继续运算
  • 结果即为num栈顶元素
#include <bits/stdc++.h>

using namespace std;

stack<char> op;
stack<int> num;
unordered_map<char, int> per{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};

void compute();

int main()
{
	string s;
	cin >> s;
	int n = s.size();
	for (int i = 0; i < n; i ++)
	{
		int j = i;
		if (isdigit(s[i]))
		{
			int x = 0;
			while (j < n && isdigit(s[j]))
			{
				x = x * 10 + s[j ++] - '0';
			}
			num.push(x);
			i = j - 1;
		}
		else if (s[i] == '(')
		{
			op.push(s[i]);
		}
		else if (s[i] == ')')
		{
			while (op.top() != '(')
			{
				compute();
			}
			op.pop();
		}
		else 
		{
			while (op.size() && per[s[i]] <= per[op.top()])
			{
				compute();
			}
			op.push(s[i]);
		}
	}
	while (op.size())
	{
		compute();
	}
	cout << num.top() << endl;
	return 0;
}

void compute()
{
	int res = 0;
	int a = num.top();
	num.pop();
	int b = num.top();
	num.pop();
	char c = op.top();
	op.pop();
	if (c == '+')
	{
		res = a + b;
	}
	if (c == '-')
	{
		res = b - a;
	}
	if (c == '*')
	{
		res = a * b;
	}
	if (c == '/')
	{
		res = b / a;
	}
	num.push(res);
}

单调栈

desc: 给定一个长度为N的数列， 输出每个数左边第一个比它小的数，如果不存在则输出-1.

做法：

  • 维护一个栈，栈顶元素维护当前输入元素左边第一个比它小的数
  • 如果栈不为空，且当前输入元素小于栈顶元素，则栈一直弹出
  • 输入一个元素，若当前栈空，则当前输入元素左边没有数，则输出-1，反之则输出栈顶元素
  • 将输入元素入栈
#include <bits/stdc++.h>

using namespace std;

stack<int> st;

int main()
{
	int n, x;
	cin >> n;
	for (int i = 0; i < n; i ++)
	{
		cin >> x;
		while (st.size() && st.top() >= x)
		{
			st.pop();
		}
		if (!st.size())
		{
			cout << "-1 ";
		}
		else 
		{
			cout << st.top() << " ";
		}
		st.push(x);
	}
	return 0;
}

单调队列（滑动窗口）

desc：对于一个数列，给定n和k，求在k个窗口中的最大最小值

  • 使用一个deque双端队列维护，队头存储最大最小值窗口值
  • 拿最小值举例，deque中存的是数组中元素的下标，先遍历一遍 1 ~ k，如果队尾元素对应的值大于等于需要添加元素，则pop_back, 然后push_back到队尾
  • 对于 k + 1 ~ n的窗口值模仿第二步， 但是对于q.front() <= i - k的元素需要pop掉，因为不存在窗口里面了
#include<bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;

int a[N];

deque<int> q_min, q_max;

int main()
{
	int n, k;
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= n; i ++)
	{
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= k; i ++)
	{
		while (q_min.size() && a[q_min.back()] >= a[i])
		{
			q_min.pop_back();
		}
		q_min.push_back(i);
	}
	printf("%d ", a[q_min.front()]);
	for (int i = k + 1; i <= n; i ++)
	{
		while (q_min.size() && a[q_min.back()] >= a[i])
		{
			q_min.pop_back();
		}
		q_min.push_back(i);
		while (q_min.front() <= i - k)
		{
			q_min.pop_front();
		}
		printf("%d ", a[q_min.front()]);
	}
	printf("\n");
	for (int i = 1; i <= k; i ++)
	{
		while (q_max.size() && a[q_max.back()] <= a[i])
		{
			q_max.pop_back();
		}
		q_max.push_back(i);
	}
	printf("%d ", a[q_max.front()]);
	for (int i = k + 1; i <= n; i ++)
	{
		while (q_max.size() && a[q_max.back()] <= a[i])
		{
			q_max.pop_back();
		}
		q_max.push_back(i);
		while (q_max.front() <= i - k)
		{
			q_max.pop_front();
		}
		printf("%d ", a[q_max.front()]);
	}
	return 0;
}

KMP

S是原串， P是模式串， 求P作为子串出现在S原串中的所有位置

next数组的含义，对于 next[j]， 是p[1, j]中前缀和后缀相同的最大长度， p[1, next[j]] = p[j - next[j] + 1, j]

  1. 求next数组（求要匹配串的最长公共前后缀的位置）
  2. 如果s[i] == p[j+1]则j继续往下走， 否则j将回溯找到ne[j]
#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;

char s[N], p[N];
int ne[N];

int main(void)
{
	int n, m;
	cin >> n >> p + 1 >> m >> s + 1;

	// 处理最长公共前后缀
	for (int i = 2, j = 0; i <= n; i ++)
	{
		while (j && p[i] != p[j + 1])
		{
			j = ne[j];
		}
		if (p[i] == p[j + 1])
		{
			j ++;
		}
		ne[i] = j;
	}
	// 匹配过程
	for (int i = 1, j = 0; i <= m; i ++)
	{
		//如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
        //用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)
		while (j && s[i] != p[j + 1])
		{
			j = ne[j];
		}
		// 当前元素匹配， j移向p串的下一位
		if (s[i] == p[j + 1])
		{
			j ++;
		}

		if (j == n)
		{
			printf("%d ", i - n);
			j = ne[j]; // 继续匹配下一个子串
		}
	}
	return 0;
}

Trie字典树

用来快速的存储和查找字符串集合的数据结构, 用字符串哈希也可以达到相同的效果。Trie树的结构如下图所示，有一根编号为0的root根节点，下面是创建的每个字符的子节点，使用son[N][26]存储树，N表示存储的字典树节点编号，26表示每个结点能连接的字符， cnt[N]表示第i个节点结尾的字符串有多少个

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int son[N][26], cnt[N], idx;
char s[N];

void insert(char str[]);
int query(char str[]);

int main(void)
{
	int n;
	char op;
	cin >> n;
	while (n --)
	{
		cin >> op >> s;
		if (op == 'I')
		{
			insert(s);
		}
		else 
		{
			cout << query(s) << endl;
		}
	}
	return 0;
}

void insert(char str[])
{
	int p = 0; // 根节点编号
	for (int i = 0; str[i]; i ++) // 遍历str
	{
		int u = str[i] - 'a'; 
		if (!son[p][u]) // 字符不存在，创建节点
		{
			son[p][u] = ++idx; 
		}
		p = son[p][u]; // 如果存在，则继续往下走
	}

	cnt[p] ++;
}

int query(char str[])
{
	int p = 0;
	for (int i = 0; str[i]; i ++)
	{
		int u = str[i] - 'a';
		if (!son[p][u]) //不存在则返回0
		{
			return 0;
		}
		p = son[p][u];
	}
	return cnt[p];
}

并查集

desc：并查集是一种可以动态维护若干个不重叠的结合，并且支持合并与查询的数据结构。擅长维护各种各样的具有传递性质的关系。

操作：

  1. find操作：查询一个元素属于哪个集合
  2. merge操作：把两个集合合并成一个集合
void merge(int a, int b)
{
        p[find(a)] = find(b);
}

int find(int a)
{
	if (p[a] != a)
	{
		p[a] = find(p[a]);
	}
	return p[a];
}

堆排序 & 模拟堆

两种建堆方式

O(nlogn): 从一个空堆开始，插入n个元素

void build_heap_1() {
  for (i = 1; i <= n; i++) up(i);
}

O(n): 从叶子的上一层开始，逐个向下调整，即合并两个已经调整好的堆

void build_heap_2() {
  for (i = n >> 1; i >= 1; i--) down(i);
}

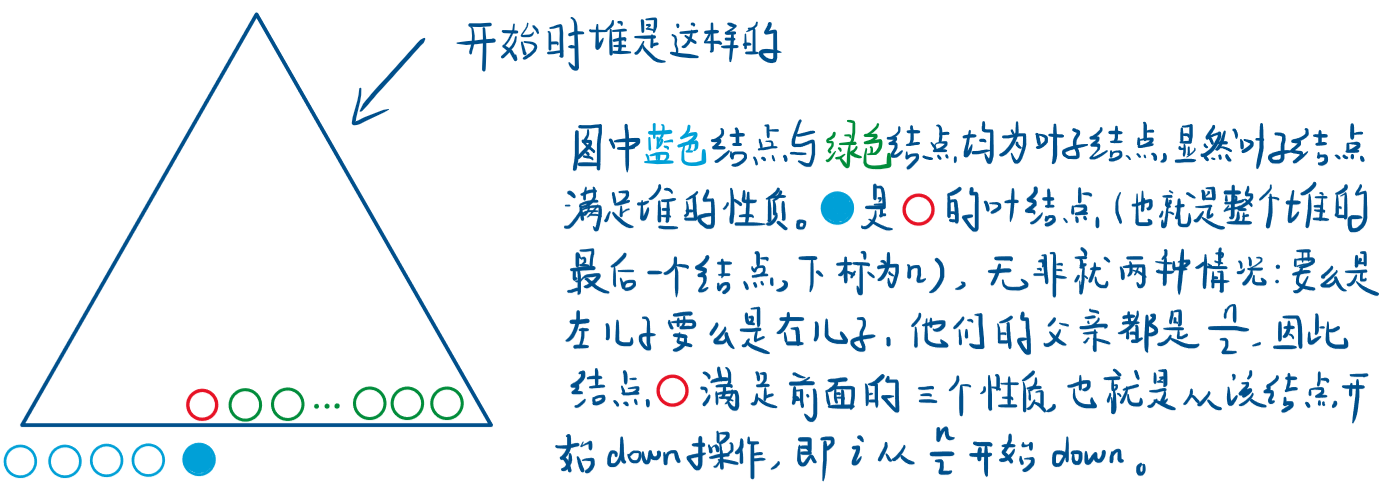
向上调整up: 如果这个结点的权值大于它父亲的权值，交换，重复此过程直到不满足或者到根。O(logn)

void up(int x) {
  while (x > 1 && h[x] > h[x / 2]) {
    swap(h[x], h[x / 2]);
    x /= 2;
  }
}

向下调整down： 在该结点的儿子中，找一个最大的，与该结点交换，重复此过程直至到底层。O(logn)

void down(int x, int size)
{
	int t = x;
	while (2 * x <= size && heap[t] > heap[2 * x]) t = 2 * x;
	while (2 * x + 1 <= size && heap[t] > heap[2 * x + 1]) t = 2 * x + 1;
	if (t != x)
	{
		swap(heap[t], heap[x]);
		down(t, size);
	}
}

对顶堆（维护中位数）

对顶堆由一个大根堆与一个小根堆组成，小根堆维护大值即前k大的值（包含第 k 个），大根堆维护小值即比第k大数小的其他数。

这两个堆构成的数据结构支持以下操作：

  • 维护：当小根堆的大小小于k时，不断将大根堆堆顶元素取出并插入小根堆，直到小根堆的大小等于k；当小根堆的大小大于k时，不断将小根堆堆顶元素取出并插入大根堆，直到小根堆的大小等于k；
  • 插入元素：若插入的元素大于等于小根堆堆顶元素，则将其插入小根堆，否则将其插入大根堆，然后维护对顶堆；
  • 查询第k大元素：小根堆堆顶元素即为所求；
  • 删除第k大元素：删除小根堆堆顶元素，然后维护对顶堆；
  • k值 +1/-1：根据新的k值直接维护对顶堆。

显然，查询第k大元素的时间复杂度是O(1)的。由于插入、删除或调整k值后，小根堆的大小与期望的 值最多相差 ，故每次维护最多只需对大根堆与小根堆中的元素进行一次调整，因此，这些操作的时间复杂度都是O(logn)的。

模拟字符串哈希（字符串前缀哈希法）

给定长度为n的字符串长度， m个询问，判断[l1, r1]与[l2, r2]的字符串是否相同

全称字符串前缀哈希法，把字符串变成一个P进制数字（哈希值），实现不同的字符串映射到不同的数字。
对形如$ X_1X_2X_3⋯X_{n−1}X_n$ 的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值。

映射公式

\[(X_1×P_{n−1}+X_2×P{n−2}+⋯+X_{n−1}×P_1+X_n×P_0)modQ \]

  1. 任意字符不可以映射成0，否则会出现不同的字符串都映射成0的情况，比如A,AA,AAA皆为0
  2. 冲突问题：通过巧妙设置P (131 或 13331) , Q (264)(264)的值，一般可以理解为不产生冲突。

问题是比较不同区间的子串是否相同，就转化为对应的哈希值是否相同。
求一个字符串的哈希值就相当于求前缀和，求一个字符串的子串哈希值就相当于求部分和。

前缀和公式h[i+1]=h[i]×P+s[i] i∈[0,n−1]h为前缀和数组，s为字符串数组
区间和公式 h[l,r]=h[r]−h[l−1]×P[r−l+1]
区间和公式的理解: ABCDE 与 ABC 的前三个字符值是一样，只差两位，
乘上 P2 把 ABC 变为 ABC00，再用 ABCDE - ABC00 得到 DE 的哈希值

#include <bits/stdc++.h>

using namespace std;

typedef unsigned long long ULL;

const int N = 100005, P = 131;

char str[N];
ULL h[N], p[N];

int check(int l, int r);

int main(void)
{
	int n, m;
	scanf("%d%d%s", &n, &m, str + 1);
	p[0] = 1;

	for (int i = 1; i <= n; i ++)
	{
		p[i] = p[i - 1] * P;
		h[i] = h[i - 1] * P + str[i];
	}
	int l1, r1, l2, r2;
	while (m --)
	{
		scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
		if (check(l1, r1) == check(l2, r2))
		{
			puts("Yes");
		}
		else 
		{
			puts("No");
		}
	}
	return 0;
}

int check(int l, int r)
{
	return h[r] - h[l - 1] * p[r - l + 1];
}
posted @ 2022-04-25 22:04  Lilyan&Code  阅读(30)  评论(0)  编辑  收藏  举报