LC 396 旋转函数

LC 396 旋转函数

题目描述

给定一个长度为 n 的整数数组 nums 。

假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组，我们定义 nums 的 旋转函数  F 为：

F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]
返回 F(0), F(1), ..., F(n-1)中的最大值 。

生成的测试用例让答案符合 32 位 整数。

示例1：

输入: nums = [4,3,2,6]
输出: 26
解释:
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。

题意

给定一个数组nums, 而旋转函数的定义为, $F(0) = 0 \times nums[0] + 1 \times nums[1] + 2 \times nums[2] + 3 \times nums[3]$, 而F(1),F(2), F(n-1)意味着旋转k = 1, k = 2 .... k = n - 1位后依照F(0)的公式计算而得到的和。

做法

O(n) 找规律， 我们可以观察示例1， F(1)是怎么由F(0)转移过来的， 我们可以看到它是由 $F(1) = F(0) - n \times (nums[n - k] + nums[0] + nums[1] + ... nums[n - k - 1])$得到的,此处的k = 1， 那么我们可不可以先预处理一遍nums数组的和，也就是$sum = nums[1] + nums[2] + ... + nums[n - 1]$,然后针对于F(1)式子的后半段$nums[0] + nums[1] + ... nums[n - k - 1]$我们可以看作sum - nums[n - k]得到呢，如下图所示， 我么可以总结规律 $F(i) = F(i - 1) + sum - n \times nums[n - k]$

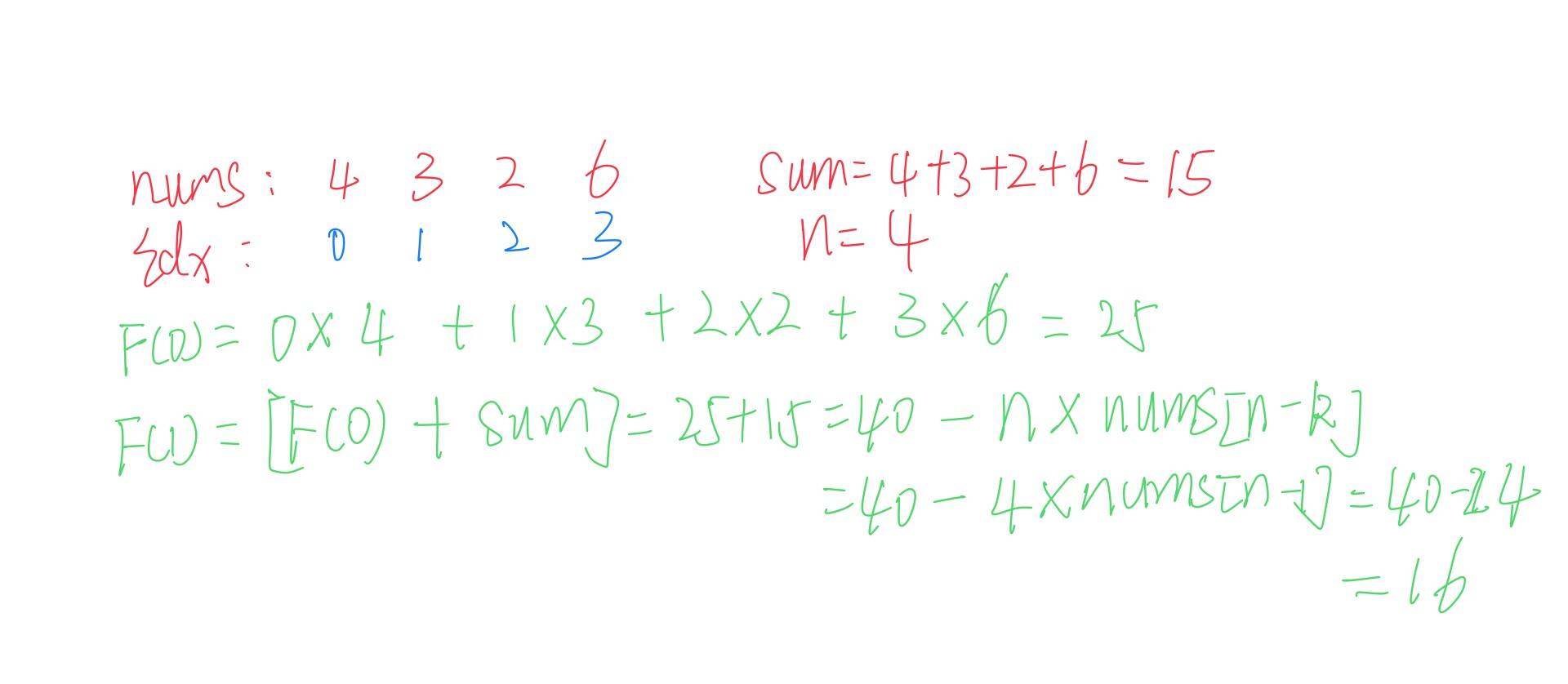
// 时间O(n), 空间O(n)
class Solution {
public:
    int maxRotateFunction(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return 0;
        int sum = 0, res = INT_MIN;
        for (auto& x : nums)
            sum += x;
        vector<int> f(n);
        int t = 0;
        for (int i = 0; i < n; i ++) t += i * nums[i];
        f[0] = t;
        res = max(res, f[0]);
        for (int i = 1; i < n; i ++) {
            f[i] = f[i - 1] + sum - n * nums[n - i];
            res = max(res, f[i]);
        }
        return res;
    }
};

// 时间O(n), 空间O(1), 由于f[n]只与f[n-1]相关，所以可以使用变量滚动代替
class Solution {
public:
    int maxRotateFunction(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return 0;
        int sum = 0, res = INT_MIN;
        for (auto& x : nums)
            sum += x;
  
        int t = 0;
        for (int i = 0; i < n; i ++) t += i * nums[i];
        res = max(res, t);
        for (int i = 1; i < n; i ++) {
            t = t + sum - n * nums[n - i];
            res = max(res, t);
        }
        return res;
    }
};