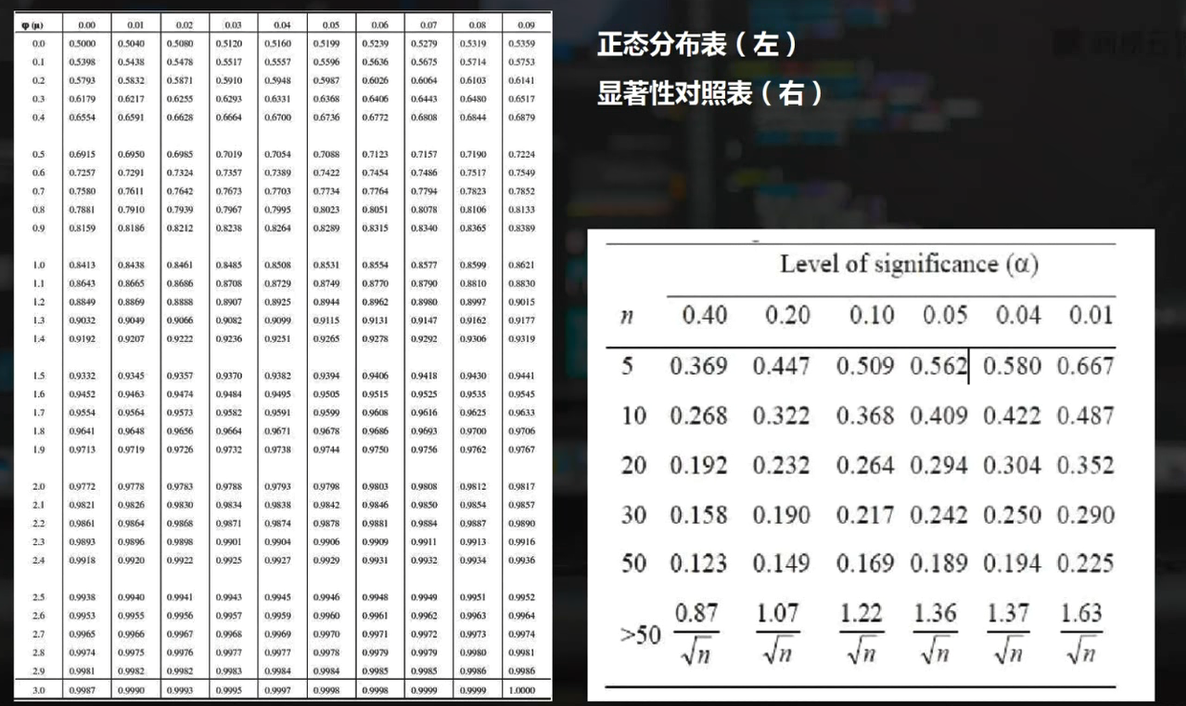
数据特征—正态性检验
正态分布
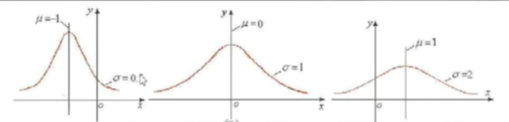
在实际数据分析过程中并不是所有数据都是满足正态分布
并不是必须满足正态分布才能分析
通过正太分布作为参考去理解事物规律

直方图初判 / QQ图判断 / K-S检验
直方图初判
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
# 直方图初判
s = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
print(s.head())
# 创建随机数据+10 就是μ往前+10
fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1) # 创建子图1
ax1.scatter(s.index, s.values)
plt.grid()
# 绘制数据分布图
ax2 = fig.add_subplot(2,1,2) # 创建子图2
s.hist(bins=30,alpha = 0.5,ax = ax2)
s.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()
# 绘制直方图
# 呈现较明显的正太性

QQ图判断
QQ图通过把测试样本数据的分位数与已知分布相比较,从而来检验数据的分布情况
QQ图是一种散点图,对应于正态分布的QQ图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图
参考直线:四分之一分位点和四分之三分位点这两点确定,看散点是否落在这条线的附近
绘制思路
① 在做好数据清洗后,对数据进行排序(次序统计量:x(1)<x(2)<....<x(n))
② 排序后,计算出每个数据对应的百分位p{i},即第i个数据x(i)为p(i)分位数,其中p(i)=(i-0.5)/n (pi有多重算法,这里以最常用方法为主)
③ 绘制直方图 + qq图,直方图作为参考
s = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
print(s.head())
# 创建随机数据 rand 就不是正态分布的
mean = s['value'].mean()
std = s['value'].std()
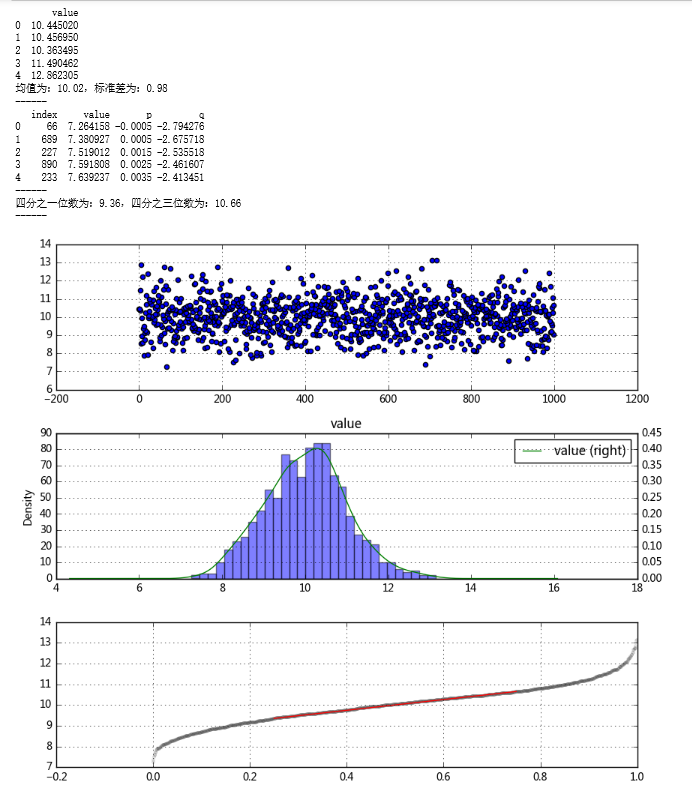
print('均值为:%.2f,标准差为:%.2f' % (mean,std))
print('------')
# 计算均值,标准差
s.sort_values(by = 'value', inplace = True) # 重新排序
s_r = s.reset_index(drop = False) # 重新排序后,更新index
s_r['p'] = (s_r.index - 0.5) / len(s_r)
s_r['q'] = (s_r['value'] - mean) / std
print(s_r.head())
print('------')
# 计算百分位数 p(i)
# 计算q值
st = s['value'].describe()
x1 ,y1 = 0.25, st['25%']
x2 ,y2 = 0.75, st['75%']
print('四分之一位数为:%.2f,四分之三位数为:%.2f' % (y1,y2))
print('------')
# 计算四分之一位数、四分之三位数
fig = plt.figure(figsize = (10,9))
ax1 = fig.add_subplot(3,1,1) # 创建子图1
ax1.scatter(s.index, s.values)
plt.grid()
# 绘制数据分布图
ax2 = fig.add_subplot(3,1,2) # 创建子图2
s.hist(bins=30,alpha = 0.5,ax = ax2)
s.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()
# 绘制直方图
ax3 = fig.add_subplot(3,1,3) # 创建子图3
ax3.plot(s_r['p'],s_r['value'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
plt.grid()
# 绘制QQ图,直线为四分之一位数、四分之三位数的连线,基本符合正态分布
KS检验
比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法
样本数据的累计频数分布于特定的理论分布比较(比如正态分布),如果两者差距小,则推论样本分布取自某特定分布。
假设检验问题:
H0:样本的总体分布 服从 某种特定分布
H1:样本的总体分布 不服从 某特定分布
Fn(x)—样本的累计分布函数
F0(x)—理论分布的分布函数
D —Fn(x)与F0(x) 差值的绝对值最大值
D = max |Fn(x)-F0(x)|
D>D(n,α) 相比较 —p>0.05 则接受H0,P<0.05则拒绝H0,接受H1
代码实现
data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
76,80,81,75,77,72,81,72,84,86,80,68,77,87,
76,77,78,92,75,80,78]
# 样本数据,35位健康男性在未进食之前的血糖浓度
df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()
std = df['value'].std()
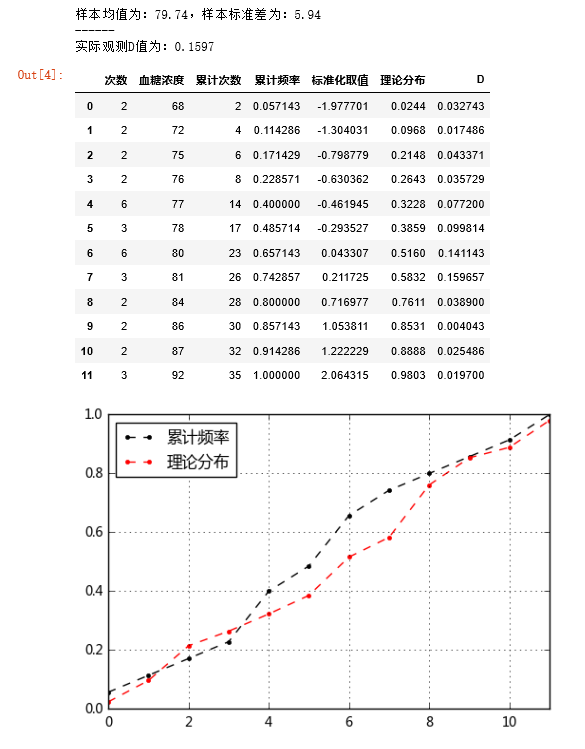
print("样本均值为:%.2f,样本标准差为:%.2f" % (u,std))
print('------')
# 查看数据基本统计量
s = df['value'].value_counts().sort_index()
df_s = pd.DataFrame({'血糖浓度':s.index,'次数':s.values})
# 创建频率数据
df_s['累计次数'] = df_s['次数'].cumsum()
df_s['累计频率'] = df_s['累计次数'] / len(data)
df_s['标准化取值'] = (df_s['血糖浓度'] - u) / std
df_s['理论分布'] =[0.0244,0.0968,0.2148,0.2643,0.3228,0.3859,0.5160,0.5832,0.7611,0.8531,0.8888,0.9803] # 通过查阅正太分布表
df_s['D'] = np.abs(df_s['累计频率'] - df_s['理论分布'])
dmax = df_s['D'].max()
print("实际观测D值为:%.4f" % dmax)
# D值序列计算结果表格
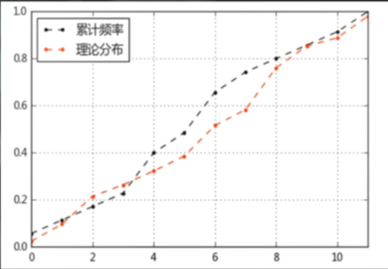
df_s['累计频率'].plot(style = '--k.')
df_s['理论分布'].plot(style = '--r.')
plt.legend(loc = 'upper left')
plt.grid()
# 密度图表示
df_s
直接用算法做KS检验
from scipy import stats
# scipy包是一个高级的科学计算库,它和Numpy联系很密切,Scipy一般都是操控Numpy数组来进行科学计算
data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
76,80,81,75,77,72,81,72,84,86,80,68,77,87,
76,77,78,92,75,80,78]
# 样本数据,35位健康男性在未进食之前的血糖浓度
df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean() # 计算均值
std = df['value'].std() # 计算标准差
stats.kstest(df['value'], 'norm', (u, std))
# .kstest方法:KS检验,参数分别是:待检验的数据,检验方法(这里设置成norm正态分布),均值与标准差
# 结果返回两个值:statistic → D值,pvalue → P值
# p值大于0.05,为正态分布