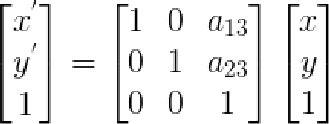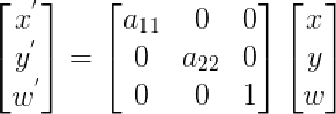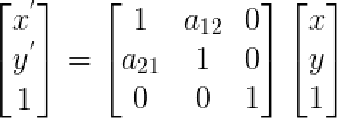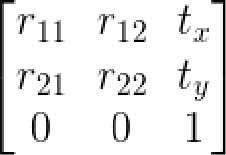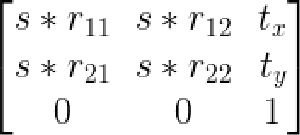基础知识：仿射变换、相似变换、等距变换等常见变换
刚体变换
只有物体的位置和朝向发生改变，而形状不变，也就是只进行平移变换和旋转变换。
射影变换（Projective Transformation）
定义：由有限次中心射影的积定义的两条直线间的一一对应变换称为一维射影变换。由有限次中心射影的积定义的两个平面之间的一一对应变换称为二维射影变换。
性质：交比不变性
如果平面上点场的点建立了一个一一对应关系，并且满足：
1> 任何共线三点的象仍是共线三点；
2> 共线四点的交比不变
则这个一一对应叫做点场的射影变换，简称射影变换。
射影变换又称作投影变换（Perspective Transformation)、透视变换(Projective Transformation)；
射影变换是最一般的线性变换，有8个自由度（虽然有9个未知数，但只与具体比率有关）；
射影变换保持重合关系和交比不变，但不会保持平行性，即它会使得仿射变换产生非线性效应;
射影变换组成了一个群，这个群被称为射影变换群，
可逆实矩阵称为一般线性群
。当把相差非零纯量因子的矩阵都视为等同时，便得到射影变换群，记为
。在平面中，射影变换为
，变换矩阵形式如下，也就是一个3阶矩阵：
当上面矩阵的最后一行为（0,0,1）时，就变成了仿射变换（
、
）不为0是射影变换与仿射变换的本质区别）。在仿射变换的前提下，若左上角
矩阵正交，该变换则变成了欧式变换，左上角矩阵行列式为1时为定向欧式变换。所以，射影变换包含了仿射变换，而仿射变换包含了欧式变换。这就是射影变换和仿射变换的关系。
上面的变换矩阵可以分成几个部分，其中：
左上角矩阵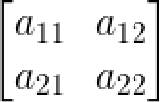
表示线性变换，比如scaling(尺度)、shearing(剪切)和ratotion(旋转)；
右上角矩阵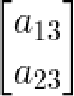
表示平移的参数，分别确定在
方向上的平移和在
方向上的平移；
左下角矩阵
用于产生透视变换。
仿射变换（Affine Transformation）
仿射变换主要包括平移变换、旋转变换、尺度变换、倾斜变换（也叫错切变换、剪切变换、偏移变换）、翻转变换，一共有六个自由度（平移包括x方向平移和y方向平移，算两个自由度）。
各变换的矩阵的形式：
1> 平移变换
2> 旋转变换
3> 尺度变换
4> 错切变换
特点：
仿射变换保持二维图形的平直性和平行性，但是角度会改变
1> 平直性：变换后直线还是直线、圆弧依旧是圆弧；
2> 平行性：平行线依旧平行，直线上点的位置顺序不变。
仿射变换的6个自由度中旋转占4个，另外两个是平移。它能保持平行性，但是不能保持垂直性（因为存在倾斜变换）。
等距变换
等距变换相当于是平移变换和旋转变换的复合，即为：
左上角2*2矩阵为旋转部分，右上角为平移因子，它有三个自由度，即旋转，x和y方向平移。等距变换前后长度、面积、线段之间额夹角都不变。
相似变换
相似变换相当于等距变换和均匀缩放的一个复合，即为：
左上角2*2矩阵为旋转部分，右上角为平移因子。它有四个自由度，即旋转、x方向平移、y方向平移和缩放因子s。相似变换后长度比、夹角保持不变，其与相似三角形类似。
虽然相似变换和仿射变换的变换矩阵一样，但是其定义不一样。因为相似变换中不存在倾斜变换（也叫错切变换、剪切变换、偏移变换）、翻转变换，而仿射变换中存在。
参考博客：
1> https://blog.csdn.net/chaolei3/article/details/79531140
