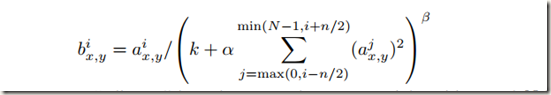深度学习基础（二）AlexNet_ImageNet Classification with Deep Convolutional Neural Networks

该论文是深度学习领域的经典之作，因为自从Alex Krizhevsky提出AlexNet并使用GPUs大幅提升训练的效率之后，深度学习在图像识别等领域掀起了研究使用的热潮。在论文中，作者训练了一个含有

60 million个参数和650000个神经元的深度卷积神经网络对ImageNet LSVRC-2010中1.2million个高分辨率彩色图像进行分类，最终取得出色的结果。在论文中作者详细描述了网络架构以及训练过

程，同时作者也对Alex网络中的一些特点及创新之处进行了介绍。下面我会记录下阅读论文时的笔记和一些理解。我在网上还发现了该论文的中文版，链接在此。

论文中比较新颖的地方如下：

网络架构中使用了ReLU Nonlinearity；
在多个GPUs上对网络模型进行分布式并行训练；
在网络中使用局部响应归一化（Local Response Normalization, RN);
在降低过拟合方面采用数据增强（Data Augmentation)和Dropout两种技术

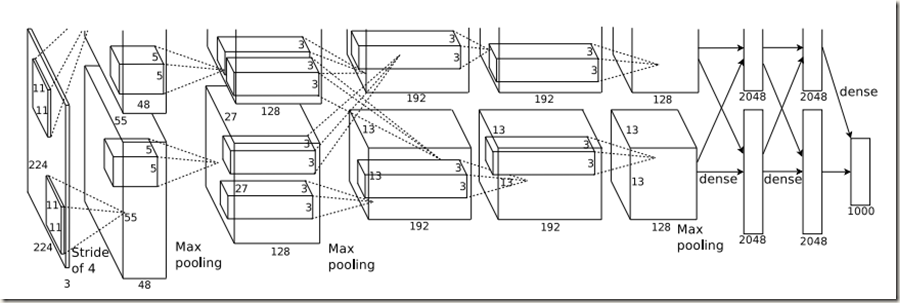
AlexNet结构如下图所示:

整体上网络一共有8层权重层，前面五层是卷积层，后面三层是全连接层，最后一个全连接层的输出被传给一个1000-way的softmax。

该网络分为上下两部分，在训练时两部分分别在两块GPU中计算，仅在部分层GPU有数据交流。比如，在第三层，计算需要上下两部分的kernels;全连接层的计算需要所有神经元的参与

从图中可知，第二、四、五层卷积层只与同一个GPU中的上一层输出直接相连；第三层卷积层与第二层输出的所有kernels相连（两个GPU）；全连接层中的神经元与上一层的所有神经元相连；第三个全连接层的输出‘Logits’被传给softamx函数转换为合理的概率值。

在第一层和第二层卷积层之后添加有局部响应归一化层；最大池化层除了存在于两个归一化层之后以外，第五层卷积层之后也接有最大池化层。而ReLU Nonlinearty被应用于每一个卷积层和全连接层的输出，这当然包括最后一个全连接层。值得注意的是，第三层卷积层使用了384个3*3*256的kernels。

3.1 ReLU Nonlinearity

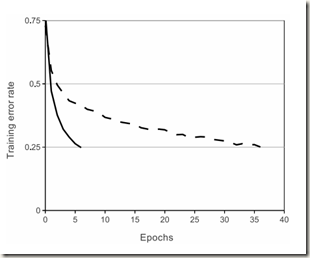
该论文使用的激活函数不是传统的sigmoid函数或tanh(x)函数，而是线性修正单元（ReLU）。使用传统激活函数时需要对输入进行归一化操作，以防止饱和带来的梯度消失问题，使得训练速度缓慢。而线性修正单元因为不存在饱和问题，所以不需要对输入归一化，且只要输入为正值，相应的神经元就会进行学习。可以看出，使用ReLUs能够缓解梯度消失的问题，加快模型的训练速度。经作者的实验证实，训练使用ReLu的卷积神经网络时训练速度比使用tanh()快六倍，如下图所示：

3.3 局部响应归一化（Local Response Normalization）

       ReLU具有良好的特性，可以在输入未进行归一化的情况下避免输出饱和。即使如此，作者发现局部响应归一化操作仍然能够有效的提高泛化能力。计算公式如下：
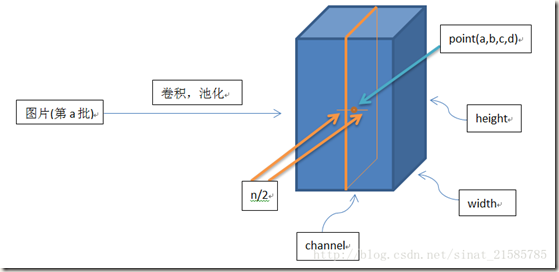
      对模型参数的理解：a是经过卷积操作并ReLUs激活后的结果。它是一个形如[batch, height, width, channel]的4-D tensor，其中batch是该批次样本数量(每一批为一张图片), 参数放在一起可以理解为一批图片中的某一个图片经过处理后的结果shape。a(x,y)是第i个kernel map(经过卷积或者池化后的结果)在空间位置(x,y)处的计算再经过激活或池化操作后的结果, 表示a中的一个位置[a, b, c, d]，可以理解成在某一张图中的某一个通道下的某个高度和某个宽度位置的点，即第a张图的第d个通道下位于[b, c]的点。b是响应归一化后的结果。N为当前层kernel map(核映射)的总数，即a的通道数。常数k, n, alpha和beta是超参数，它们的取值使用一个验证集确定，论文中取为：k=2,n=5,alpha=10e-4,bata=0.75。kernel map的顺序是任意的，但是需要在训练开始之前确定下来。a, n/2, k, alpha, beta分别与函数tf.nn.local_response_normalization(tf.nn.lrn)的参数input, depth_ridius, bias, alpha, beta对应。函数的参数名称可以直观的解释公式中参数意义。另外需要注意的是，∑叠加的方向是沿着通道方向的，也就是一个点a(x,y)同方向的前面n/2个通道（最小为第0个通道）和后面n/2个通道（最大为第d-个通道）的点的平方和（共n+1个点）。这里实际上就是将a沿通道方向拆成d个3-D矩阵，所以叠加的方向也在通道方向上。如下图所示：
       帮助理解Local Response Normalization的示例：
import os
import tensorflow as tf
import numpy as np

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# data_form='NHWC'
a = np.array([i for i in range(1, 33)]).reshape([2, 2, 2, 4])
b = tf.nn.lrn(input=a, depth_radius=2, bias=0, alpha=1, beta=1)

with tf.Session() as sess:
    print(a)
    print('#############')
    print(b.eval())
结果：
[[[[ 1 2 3 4]
    [ 5 6 7 8]]

[[ 9 10 11 12]
    [13 14 15 16]]]

[[[17 18 19 20]
    [21 22 23 24]]

[[25 26 27 28]
    [29 30 31 32]]]]
#############
[[[[ 0.07142857 0.06666667 0.10000001 0.13793103]
    [ 0.04545454 0.03448276 0.04022989 0.05369128]]

[[ 0.02980132 0.02242153 0.02466368 0.03287672]
    [ 0.0220339   0.01654846 0.0177305   0.02363368]]]

[[[ 0.0174538   0.01310044 0.01382824 0.01843318]
    [ 0.01444292 0.01083744 0.01133005 0.01510384]]

[[ 0.01231527 0.00923952 0.00959488 0.01279123]
    [ 0.01073279 0.00805153 0.00831991 0.01109185]]]]

   ######根据’NHWC’格式可知a中不同彩色区域属于不同的维度，比如，[1 2 3 4]是某点在通道维度上的数值，则1处值的计算为1/(0+1*(1^2+2^2+3^2))^1=0.07142857;同样，对于[25 26 27 28]，在27处值的计算为26/(0+1*(25^2+26^2+27^2+28^2))^1=0.00959488. (N=4,n/2=2,bias=0, alpha=1, beta=1)
      局部响应的由来借鉴了真实神经元的侧抑制概念（被激活的神经元抑制相邻神经元），所以归一化的目的是抑制。局部响应归一化层模仿生物神经系统的侧抑制机制，为局部神经元的活动创建竞争机制，使得响应比较大的值相对更大，并抑制其他反馈较小的神经元，提高模型泛化能力，能将识别率提高1-2%。通常，局部响应归一化会被应用在某些层的激活、池化操作之后。
      部分研究发现，局部响应归一化并不能提高模型的准确度和泛化能力，反而会降低预测的准确性，并为GPU增加计算负担，降低训练速度。我认为局部相应归一化应该只适用于部分问题，LRN是否有助于模型性能的提升估计只能进行尝试比较了。
      tensorflow中对应的函数为tf.nn.local_response_normalization
      相关链接：https://blog.csdn.net/yangdashi888/article/details/77918311
                    https://blog.csdn.net/sinat_21585785/article/details/75087768

posted @ 2019-03-24 14:35 Lilu1223 Views(330) Comments(0) Edit 收藏举报

刷新页面返回顶部

torich

深度学习基础（二）AlexNet_ImageNet Classification with Deep Convolutional Neural Networks

公告