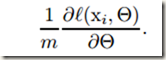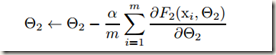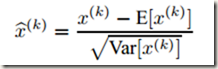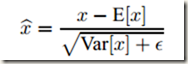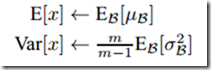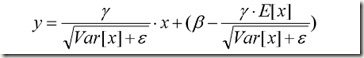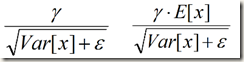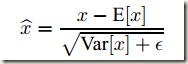图像分类（二）GoogLenet Inception_v2：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
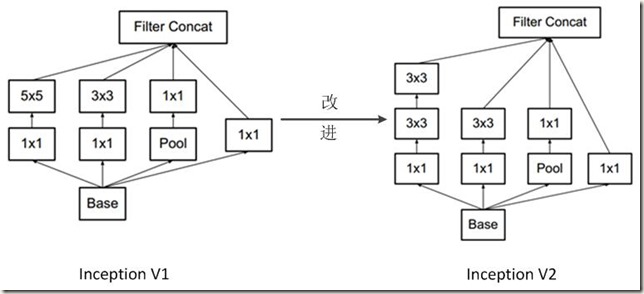
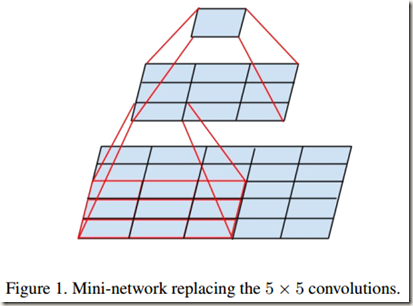
Inception V2网络中的代表是加入了BN（Batch Normalization）层，并且使用 2个 3*3卷积替代 1个5*5卷积的改进版，如下图所示：
其特点如下：
- 学习VGG用2个 3*3卷积代替 Inception V1中的 5*5大卷积。这样做在减少参数（3*3*2+2 –> 5*5+1）的同时可以建立更多的非线性变换，增强网络对特征的学习能力。如下图所示，2个 3*3卷积的效果与一个 5*5 卷积的效果类似：
- 在 Inception V1中加入BN层，以减少 Internal Convariate Shift，使每一层的输出都规范化到均值为0方差为1的高斯分布。这样改进的好处是可以增加模型的鲁棒性、可以以更大的学习速率训练，使网络收敛更快、参数的初始化可以更加随意，同时作为一种正则化技术，可以减少 dropout层的使用，甚至不使用 dropout层；缺点就是module的权重增加了25%，计算消耗增加了30%
- Inception module的深度增加（因为 2个3*3 替换了 5*5，还在所有卷积层和池化层之后添加了BN层），整体增加了9层（8层BN层+1层卷积层）
下面的内容以论文和博客为主，帮助我们一步一步地理解什么是 Batch Normalization
Batch Normalization
在训练深度神经网络时，如果previous layers的参数发生变化，那后面每层的输入分布也会跟着变化，这会使得训练变得复杂。复杂体现在，训练更容易遭遇非线性饱和；同时，为了避免梯度消失和梯度爆炸，需要设置较低的学习速率（ Learning rate）和谨慎地初始化参数，显然这会降低网络的训练速度。作者在论文中将这种现象称为”Internal Covariate Shift”，并通过 normalize layer inputs解决了这个问题。这种方法的优势在于，将 normalization 当做模型结构的一部分，而且在训练时对每一个 mini-batch 进行归一化，所以该方法被称为 Batch Normalization。BN所带来的好处很明显：训练时可以使用更高的学习速率加快训练速度，因此仅需更少的 trianing steps就能达到与之前相同的精度；能够更随意地初始化参数；BN相当于是一个 regularizer，有些情况下甚至可以不必使用 dropout。可见，BN的作用就是通过使每一层深度神经网络的输入保持相同的分布达到消除 Internal covariate shift的目的，这样网络就可以更快地收敛。
（论文首先引出了mini-batch SGD，并罗列了它的优点，因为后面介绍的BN是基于 mini-batch SGD的）
目前训练深度神经网络最有效的方法就是 stochastic gradient descent(SGD，即mini-batch SGD)及其变体，如momentum、Adagrad、Adadelta等。
Batch gradient descent(BGD)通过最小化 loss 优化网络参数，如下：
SGD用mini batch逼近所有训练样本的loss对各参数的梯度，计算如下，式中m是一个batch内的样本数，其它符号的含义与上面的公式相同：
与one example SGD相比，mini-batch SGD有如下优势：
- 根据mini batch的损失计算得到的梯度是对整个训练集上的梯度的估计，并且batch size越大估计值越接近整个训练集对应的梯度
- 在mini batch上的计算比单个样本的m次计算要高效很多，因为现在的计算平台支持并行计算
（先引出 covariate shift概念，接着说明固定 sub-network的输入分布的重要性，最会又说明固定 layers的输入分布对 layers也有积极影响）
随机梯度下降法虽然简单高效，但trianing时 preceding layers的参数变化会影响每一层输入，这一点让训练变得复杂起来。因为在训练过程中，如果各层参数不停地变化，那么每个隐层网络的输入分布（input distribution）也就随着变化，致使后面的网络需要不断地学习适应新的分布。为此，在训练时不得不谨慎地调整模型的超参数，尤其是学习速率和模型参数的初始值，以防止梯度消失和梯度爆炸（网络在适应新的分布时梯度波动较大，较高的学习速率或不恰当的初始化参数会使梯度爆炸或消失，如果使用非线性激活的话就很有可能导致非线性饱和）。如果是 learning system整个系统的输入分布改变，那么可以说该系统发生了 covariate shift。这个问题可以通过 domain adaptation解决。不过，我们更在意的是，covariate shift的概念可以从局限的整个learning system拓展到 learning system 的局部结构上，比如系统中的一个 sub-network或 a layer。下面假设一个网络含有子网络F2，其损失计算如下：
式中，F1 和 F2是任意的转换。
的学习可以视为对输入为
的sub-network的学习，其梯度下降步骤如下，式中m是mini batch的size，
是学习速率：
可以看出，子网络 F2 相当于是一个输入为 x 的独立网络。但是我们都知道，机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据都是满足相同分布的，这是通过训练数据获得的模型能在测试集获得较好效果的一个基本保障。所以，上述sub-network的训练也应该满足该假设，即输入x 的分布不能随 previous layers 参数的改变而不断改变，应该固定在同一分布。因此，保持 x（sub-network的输入）的分布随时间不变对 sub-network 是很有利的，那样的话sub-network训练时参数就不需要不断地适应 x 分布的改变。
事实上，固定sub-network的输入分布对sub-network之外的 layers 也有积极的影响。我们都知道使用 Sigmoid激活函数训练时容易产生饱和问题，使梯度消失，通常可以通过使用 Rectified Linear Units、更低的学习速率和合理的初始化解决。但是，如果我们能确保非线性输入的分布更稳定的话，那优化器陷入饱和的可能性会大大降低，训练的速度也会因此加快（平常训练时会有部分units进入饱和状态，不过随着训练的推进，未饱和神经元的参数不断更新，逐渐使得部分饱和的神经元退出饱和。显然，饱和会减缓训练）。
（引出 Internal Covariate Shift，并引出解决方法BN）
作者至此已将covariate shift的概念拓展到深度网络内部，同时把训练时深度网络内部节点的分布变化称为 Internal Covariate Shift。那么如果解决 internal covariate shift这个问题呢？为此，作者提出了一种新机制，那就是 Batch Normalization。它通过固定 layer inputs的均值（means）和方差(variances)减少internal covariate shift，这样做有如下几点优点：
- 极大地加速了深度神经网络的训练
- 降低了梯度对网络参数尺度和初始值尺度的依赖，这有助于梯度的反向传播
- 正则化了模型，并降低了对 Dropout的需求
- 通过防止网络陷入饱和模式（Saturated modes），使得网络使用饱和非线性激活函数（saturating nonlinearities）成为可能
（下面是BN的实现细节）
Batch Normalization是作者受到白化操作（whiten）启发而提出的。众所周知，网络的输入经过白化处理（线性变换成均值为0，方差为1）和去相关处理后会加快网络训练时的收敛速度。那么，类似的，白化网络的每一层输入应该也能带来很多益处。那么能不能每层的输入都做白化呢？经过分析，作者认为这种做法不可取，于是在仔细比较分析后确定了最终的方法，即BN。事实上BN就是对深层神经网络的神经元的激活值做简化版本的白化操作。
由于对每一层的输入进行完全的白化是昂贵的，且并不是处处可微，所以作者就对其做了两个必要的简化处理：一是，不联合白化 layer inputs和 outputs，而是独立地归一化每个标量形式的特征（scalar feature），使之均值为0，方差为1。比如，对于一个拥有 d 维输入
的 layer，会按照下面的公式 normalize 每一维，其中期望 E 和方差 Var 是在训练数据集上计算得到的（后面会简化成mini batch），xk 代表该层输入的一个神经元：
这样处理后也可以加快收敛，甚至在特征没有去相关的情况下也可以。该操作的基本思想相当直观：因为在深层神经网络中，非线性变化（后面会说，BN一般放在激活层之前）之前的激活值（activation，即 x=Wu+B）随着训练进行，其分布会发生偏移或者变动。一般是整体分布逐渐往非线性函数的易饱和区域靠近，从而导致反向传播时低层神经网络（不是高层，如果是高层的话整个网络就无法训练了）的梯度消失（为0），这是训练深层神经网络时收敛较慢的本质原因。既然整体分布处在不佳的位置，那就通过一定的规范化手段把它强行拉到均值为0方差为1的标准正态分布（之前也是正态分布，但是方差和均值比较不合理），这样激活值就能落在非线性函数对输入比较敏感的区域从而缓解梯度饱和问题，加快收敛速度。如果觉得抽象的话可以借助Sigmoid函数和正态分布曲线想象，或参考这里。
经过上述介绍的变换后，大部分激活值（normalized activation）都落入激活函数的中间区域。如果激活函数类似于sigmoid，那么activation就会对应sigmiod函数的线性区域，这时原来的非线性函数就与线性函数无异，网络层需要表示的内容也被改变。此外，在非线性函数相当于线性函数的时，即使有多层激活层也是没有意义的，因为多层线性网络与一层线性网络是等价的（可以写几个线性表达式嵌套看一下，确实如此），这意味着网络的表示能力下降了，即使是深度网络也没有意义。为了保证激活函数的非线性，作者为每个变换后的激活值添加了两个参数
，分别用来scale（缩放）和shift（平移）变换后的激活值，即：
这两个参数会和原始模型的参数在一起学习，用来恢复模型的 representation power。实际上，如果设置
、
，那就可以恢复到变换前的激活值。直观上可以理解为：scale和shift把变换后的激活值从标准正态分布左移或者右移一些并变胖或变瘦一点，这样就等价于将原本落在激活函数中间线性区域的激活值往非线性区域调整了一下。最终学到的scale和shift应该能够在二者之间取得平衡，使得既能利用非线性表示能力强的优点，又能避免太靠近非线性区域致使接近饱和或者饱和，减慢收敛速度。实际上，每个normalized activation(第一个简化分两步，第一步是normalization,第二步是 linear transformation)都可以被视为一个由上图中linear transformation组成的sub-network的输入。
第二个简化措施是，使用mini batch的均值和方差对激活值进行归一化。在使用批量梯度下降法（Batch gradient descent）训练时，归一化激活值自然是利用整个训练集的统计信息。然而，在使用SGD时再这样做的话显然不切实际。考虑到mini-batch SGD使用mini batch估计整个数据集，作者就做了替换。
（接下来是对mini batch内的一个activation x进行normalization的算法过程）
假设一个size为m的 mini batch B。既然normalization是独立地应用于每个activation，那么接下来就只关注一个特定的activation xk，并且忽略分类标识k，所以该activation就有m个值（batch内有m个样本）
归一化后的值记为
，线性变换（linear transformation）后的值记为
。整个 Batch Normalization Transform 记为
那么 BN Transform 的算法流程如下，表中
是为了增加数值稳定加到方差上的一个常数：
可见，BN Transform可以被添加到网络中来操作任何一个激活值，整个过程仅依赖mini batch。
（下面是 Batch-Normalized Networks的 training和 Inference）
为了对网络进行 Batch Normalize，需要先指定要进行BN的activations的集合，然后为每个activation在网络结构中插入BN Transform（如Algorithm所示）。使用BN的深度神经网络需要使用m>1的梯度下降法或者其变体进行训练（m=1的one example不行，与Inference类似），因为BN依赖mini-batch。
BN在训练时可以根据mini-batch估计出均值和方差，但是在推理（Inference）的过程中，输入就只有一个实例，无法依照下面的公式进行计算。
既然没有mini batch数据来获得需要的统计量，那就另寻他路。先前对activations进行normalization时本来需要使用整个训练集的方差和均值，但是为了计算方便就用mini batch的统计量替代了，那么现在推理时正好可以用回全局的统计量。
和先前一样，我们依然不需要计算整个训练集来获取统计信息。因为每次在做mini-batch训练时，我们都计算了mini batch的方差和均值，现在要全局统计量的话，我们只需要把每个min batch的均值和方差统计量记住，然后对这些均值和方差求数学期望即可得到全局统计量，即;
得到均值和方差之后，再加上每个隐层神经元训练好的scale和shift参数，就可以在inference的时候对每个神经元的激活值 x 进行BN Transform了。在推理过程中用下列公式替换训练时的BN 变换：
式中 x 是未经过normalization的激活值，所以上面的公式其实包含了normalization和 linear transformation两步。通过简单的合并就能发现上面的公式与训练时的BN Transform公式一模一样，而作者之所以这样写应该是为了在实际运行时减少计算量。为什么可以减少计算量呢？因为对每个隐层节点来说
都是固定值，这样的话这两个值可以事先存好，在推理时直接使用就行，不必每次推理时每个激活值都按照
重新计算一遍。如果网络中使用BN的节点较多的话，这样可以减少大量的计算。
最后，附上训练 Batch-Normalized Network的完整算法：
参考资料
