Josephus 约瑟夫环问题图解

经典案例#

1. 古代某法官要判决 n 个犯人死刑，他有一条荒唐的逻辑，将犯人首尾的相接排成圆圈，然后从第 start 开始数起，每数到第 distance 个犯人，就拉出来处决；然后又数 distance 个，数到的犯人又拉出来处决，依次类推。剩下的最后一人可以豁免。

2. 一群猴子排成一圈，按1，2，…，n依次编号。然后从第 start 只开始数，数到第 distance 只，把它踢出圈，从它后面再开始数，再数到第 distance 只，在把它踢出去…，如此不停的进行下去，直到最后只剩下一只猴子为止，那只猴子就叫做大王。

题意说明#

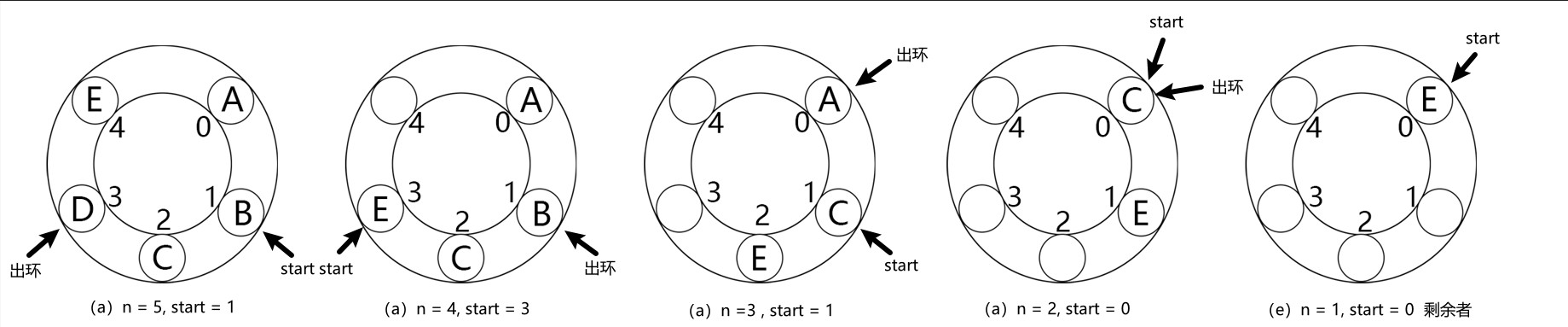
采用线性表标记 n 个人，设 n = 5, start = 1, distance = 3, 5 个人分别标记为 A B C D E， josephus(5,1,3) 环问题的求解过程如图：

算法描述#

求解 Josephus 环问题， n个人，从 start 开始计数，每次数到 distance 的人出环

Java 实现#

/**
 * @param n        n 个人
 * @param start    从 start 开始计数
 * @param distance 每次数到 distance的人出环
 * @return int 最后的结果
 */
public static int josephus(int n, int start, int distance) {
    if (n <= 0 || start < 0 || start >= n || distance <= 0 || distance >= n) {
        throw new IllegalArgumentException("参数异常");
    }
    // 创建一个线性表对象 List 集合并插入从 1 开始的 n 个元素
    ArrayList<Integer> arr = new ArrayList<>();
    for (int i = 1; i <= n; i++) {
        arr.add(i);
    }
    while (n > 1) {
        // start 循环计数到 distance, 第 start 个元素出环即删除，其后若干元素向前移动一位
        int len = arr.size();
        // 计算出下一次出环的人 (当前计数 + 每次数的数量 - 1) % 当前人数  O(n)
        // start 本指向上一次出环的元素，但出环后元素全部向前移动一位，start 也将指向下一为元素，所以需要减一
        start = (start + distance - 1) % n;
        arr.remove(start);
        n--;
    }
    return arr.get(0);
}