DirectX11:GPU基数排序
DirectX11:GPU基数排序
CPU基数排序
基数排序(radix sort)的基本思想是从最低位开始(LSD),按照当前位的数值进行排序得到一个新的序列,对新序列依据高一位的数值重新排序,这样依次直到最高位,得到的数列就是一个有序数列。基数排序众所周知是一个无需进行比较的排序算法。
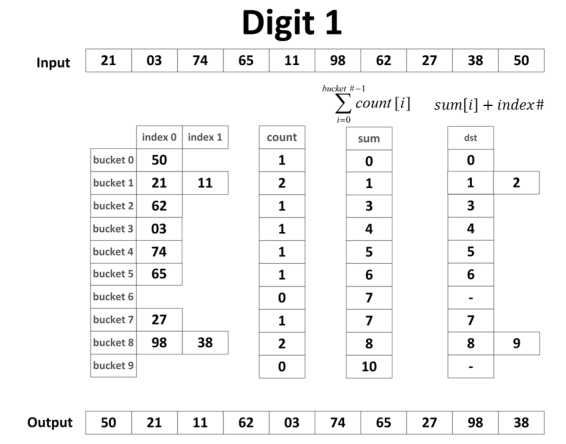
具体过程如上图所示,上图是CPU版本的基数排序,算法过程在这就不展开讲。
GPU基数排序
对于GPU的基数排序主要是针对数据的每一位进行排序,例如下图是对三位二进制按照LSD进行排序的过程(\(R=2^3\))
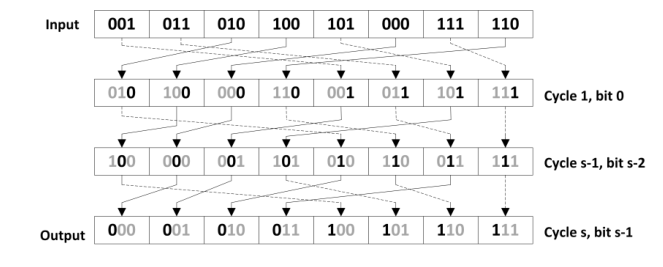
网上对于GPU版本基数排序感觉资源并不是很多,而且大部分都是CUDA版本,由于我并没学习过CUDA,所以我在阅读了一些论文资料后,实现了一个基于DirectX11的计算着色器(Computer Shader)的GPU基数排序。后面的讨论全部将以32位无符号整数进行讨论。
对于其实现过程希望你能对DirectX11、计算着色器、缓冲区资源,或者说对CUDA有一定了解,以下是我所学习(使用)的一些内容。
| DirectX11 With Windows SDK--00 目录 |
|---|
| 深入理解与使用缓冲区资源(结构化缓冲区/有类型缓冲区) |
| 26 计算着色器:入门 |
| 27计算着色器:双调排序 |
前缀和(prefix sum)与并行规约
为了后续排序算法我们得首先了解下前缀和以及并行规约算法。
根据Blelloch所定义的前缀和操作如下:有一系列无序的输入数据:\([a_0,a_1,...,a_{n-1}]\),然后返回以下数组:\([a_0,(a_0\bigoplus a_1),...,(a_0\bigoplus a_1\bigoplus...\bigoplus a_{n-2})]\)。如果\(\bigoplus\)为加法,我们便可以得到其前缀和。
我们一般在CPU中实现前缀和非常简单,只需要一趟循环即可完成。
//exclusive prefix sum
std::vector<int> prefixSum;
void prefixSum(const std::vector<int>& nums)
{
prefixSum.resize(nums.size());
for(int i=1;i<nums.size();++i)
{
prefixSum[i]=prefixsum[i-1]+nums[i-1];
}
}
但是不可能在GPU上写这种循环算法,因此我们要采用并行规约算法去进行求前缀和。
最简单的并行规约算法(即朴素规约算法)如下:
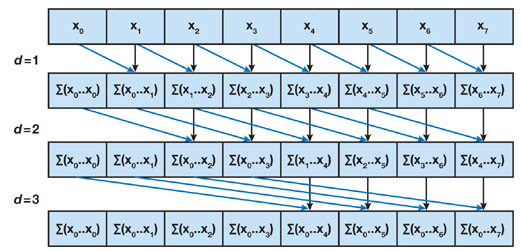
1: for d = 1 to log2 n do
2: for all k in parallel (并行) do
3: if k < 2^d then
4: x[k] = x[k – 2^(d-1)] + x[k]
这样我们在GPU中得到输入数组的前缀和。但是由于这种朴素规约方式在大型阵列上并不高效。
所以提出了以下的并行规约求前缀和的算法,他是基于Blelloch(1990)提出的算法,想法是在输入数据上建立一个平衡二叉搜索树,然后在根目录中进行扫描以计算前缀和。
一个具有n个叶子节点的二叉树有\(log_2n\)层,每一层d有\(2^d\)个节点,如果我们对每个节点执行一次加法,那么我们将在树的单次遍历过程中只执行了\(O(n)\)次加法。
我们建立的树并不是一个实际上的数据结构,只是用来确定每个线程在遍历过程中每个步骤应该做什么。在这个扫描算法中,我们在共享内存中的数组上执行适当的操作。整个算法由两个阶段组成:归约阶段(上行阶段)和下扫阶段。
-
在归约阶段,我们从叶子节点到根节点进行遍历计算树的内部节点的部分和,根节点保存数组中所有节点的和。如下图所示
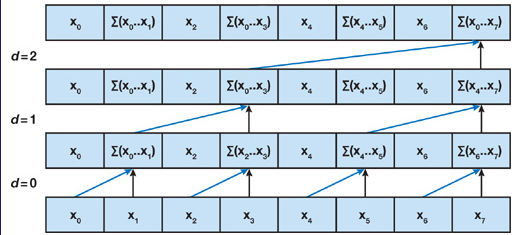
伪代码如下:
1: for d = 0 to log2 n – 1 do 2: for all k = 0 to n – 1 by 2^(d+1) in parallel do 3: x[k + 2^(d+1) – 1] = x[k + 2^d – 1] + x[k + 2^d +1 – 1] -
在下扫阶段,我们将从根节点开始向下遍历,使用归约阶段的部分和在数组上进行适当的扫描。我们首先在树的根部插入零,在每一步中,当前层次的每个节点将其自己的值传递给其左子节点,其值与其左子树的前值之和传递给其右子节点。如下图所示:
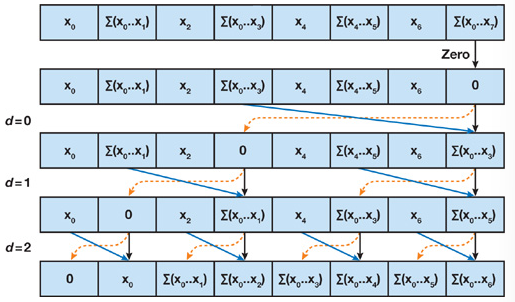
伪代码如下:
1: x[n – 1] = 0 2: for d = log_2 n – 1 down to 0 do 3: for all k = 0 to n – 1 by 2^d +1 in parallel do 4: t = x[k + 2^d – 1] 5: x[k + 2^d – 1] = x[k + 2^d +1 – 1] 6: x[k + 2^d +1 – 1] = t + x[k + 2^d +1 – 1]
HLSL核心代码如下:
#define THREAD_NUM_X 1024
groupshared uint localPrefix[THREAD_NUM_X];
//excusive scan
void PresumLocal(uint GI : SV_GroupIndex)
{
//up sweep
uint d = 0;
uint i = 0;
uint offset = 1;
uint totalNum = THREAD_NUM_X;
[unroll]
for (d = totalNum>>1; d > 0; d >>= 1)
{
GroupMemoryBarrierWithGroupSync();
if (GI < d)
{
uint ai = offset * (2 * GI + 1) - 1;
uint bi = offset * (2 * GI + 2) - 1;
localPrefix[bi] += localPrefix[ai];
}
offset *= 2;
}
//clear the last element
if (GI == 0)
{
localPrefix[totalNum-1] = 0;
}
GroupMemoryBarrierWithGroupSync();
//Down-sweep
[unroll]
for (d = 1; d < totalNum; d *= 2)
{
offset >>= 1;
GroupMemoryBarrierWithGroupSync();
if (GI < d)
{
uint ai = offset * (2 * GI + 1) - 1;
uint bi = offset * (2 * GI + 2) - 1;
uint tmp = localPrefix[ai];
localPrefix[ai] = localPrefix[bi];
localPrefix[bi] += tmp;
}
}
GroupMemoryBarrierWithGroupSync();
}
排序算法过程
以下的算法过程是我基于一些论文,按照自己想法的实现的,暂时未进行效率比较,后续会考虑进行优化以及有时间会将其效果与CPU排序算法,双调排序,采用原子操作进行算法效率的比较。
首先我们讲输入的数据按照线程组进行分块,分块后组内进行操作。我们按照低4位进行排序一趟(即\(R=2^4=16\)),32位数据最多进行8趟循环即可完成排序。每一趟循环过程如下:
-
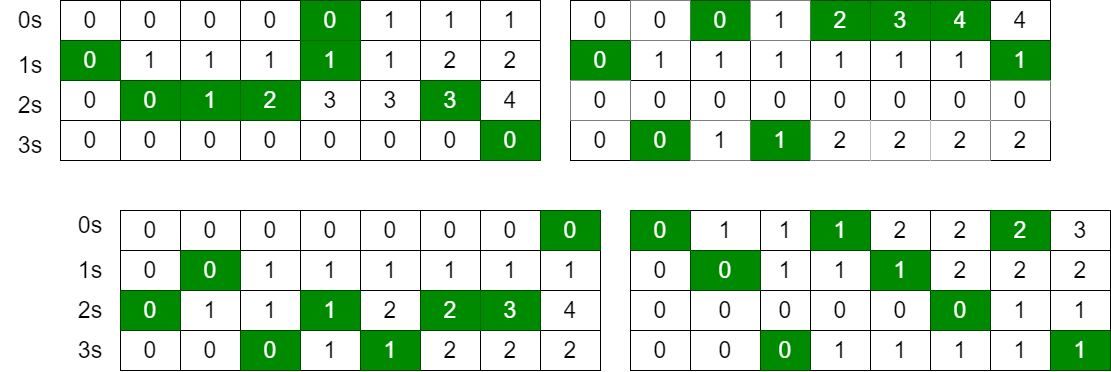
我们首先提取4位数据,根据16个基数进行求前缀和(即进行16次循环);若当前4位数据与当前循环的基数相等,则共享内存对应数组赋值为1,反之为0,如下图所示(基数为\(R=2^2\)):

然后在共享内存中求其前缀和,最后将其前缀和(需当前4位数据与当前循环的基数相等)作为本地偏移输出到全局内存之中,以及将每个线程组中当前循环的基数的计数总数输出到全局内存的计数桶(形式上是一个二维矩阵,行号为线程组序号,列号为基数)之中。本地偏移计算结果如下图所示:
计数桶计算结果如下图所示:
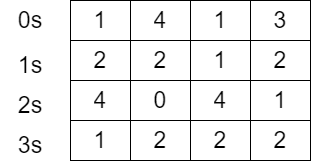
-
将第一步中得到的计数桶进行求前缀和(与第一步求前缀和算法相同),并输出到全局内存之中。计算结果如下图所示:
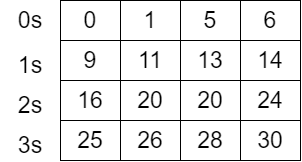
-
根据第一步计算出每个基数的本地偏移以及第二步进行的总数前缀和相加得到对应的全局位置索引,将当前数据输出到全局数组的对应的全局索引之中。
排序算法HLSL核心代码
//RadixSortCount
[numthreads(THREAD_NUM_X, 1, 1)]
void CS(uint GI : SV_GroupIndex, uint3 DTid : SV_DispatchThreadID
,uint3 Gid:SV_GroupID)
{
//get curr digit correspend to 4-bit LSD
uint digit = get4Bits(g_cellHash[DTid.x], g_CurrIteration);
//counter
[unroll(RADIX_R)]
for (uint r = 0; r < RADIX_R; ++r)
{
//load to share memory
localPrefix[GI] = (digit == r ? 1 : 0);
GroupMemoryBarrierWithGroupSync();
//prefix sum according to r in this blocks
PresumLocal(GI);
//ouput the total sum to counter
if (GI == THREAD_NUM_X - 1)
{
uint counterIndex = r * g_BlocksNums + Gid.x;
uint counter=localPrefix[GI];
if (digit == r)
{
counter++;
}
g_SrcCounters[counterIndex] = counter;
}
//output prefix sum according to r
if(digit==r)
{
g_SrcPrefix[DTid.x] = localPrefix[GI];
}
GroupMemoryBarrierWithGroupSync();
}
}
//RadixSortCountersPrefix_CS
[numthreads(THREAD_NUM_X, 1, 1)]
void CS(uint3 DTid : SV_DispatchThreadID,uint GI : SV_GroupIndex,uint3 Gid:SV_GroupID)
{
//load date to shared memort
if (DTid.x < g_CounterNums)
{
localPrefix[GI.x] = g_SrcCounters[DTid.x];
}
else
{
localPrefix[GI.x] = 0;
}
GroupMemoryBarrierWithGroupSync();
//calc counter prefix sum
PresumLocalCounter(GI);
//ouput
if (DTid.x < g_CounterNums)
{
g_DstCounters[DTid.x] = localPrefix[GI];
}
DeviceMemoryBarrierWithGroupSync();
if (Gid.x > 0)
{
//get pred sum
uint sum = 0;
for (uint i = 0; i < Gid.x; ++i)
{
sum += g_DstCounters[(i + 1) * THREAD_NUM_X - 1]+g_SrcCounters[(i + 1) * THREAD_NUM_X - 1];
}
LocalCounterAdd(GI, sum);
//output
if (DTid.x < g_CounterNums)
{
g_DstCounters[DTid.x] = localPrefix[GI];
}
}
}
//RadixSortDispatch
[numthreads(THREAD_NUM_X, 1, 1)]
void CS(uint3 DTid : SV_DispatchThreadID,uint3 Gid:SV_GroupID)
{
//get curr digit
uint digit = get4Bits(g_cellHash[DTid.x], g_CurrIteration);
//global dispatch
uint counterIndex = digit * g_BlocksNums + Gid.x;
uint globalPos = g_SrcPrefix[DTid.x] + g_DstCounters[counterIndex];
g_DstKey[globalPos] = g_cellHash[DTid.x];
g_DstVal[globalPos] = g_cellIndexs[DTid.x];
}
排序算法效率
目前排序算法用于流体模拟中的领域搜索中,总共排序27648个数据,平均耗时:0.8ms左右
参考资源
Chapter 39. Parallel Prefix Sum (Scan) with CUDA
[1] Merrill D, Grimshaw A. High performance and scalable radix sorting: A case study of implementing dynamic parallelism for GPU computing[J]. Parallel Processing Letters, 2011, 21(02): 245-272.
[2] Sengupta S, Harris M, Garland M. Efficient parallel scan algorithms for GPUs[J]. NVIDIA, Santa Clara, CA, Tech. Rep. NVR-2008-003, 2008, 1(1): 1-17.
[3] Ha L, Krüger J, Silva C T. Fast Four‐Way Parallel Radix Sorting on GPUs[C]//Computer Graphics Forum. Oxford, UK: Blackwell Publishing Ltd, 2009, 28(8): 2368-2378
[4] Garcia A, Flores J O A, Pinto U O, et al. Fast Data Parallel Radix Sort Implementation in DirectX 11 Compute Shader to Accelerate Ray Tracing Algorithms[C]//EURASIA GRAPHICS: International Conference on Computer Graphics, Animation and Gaming Technologies. 2014: 27-36.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号