Loading

数据结构笔记三：栈和队列

目录

栈

基本概念

栈（Stack）是只允许在一端进行插入或删除的线性表。

栈顶：线性表允许进行插入删除的一端。

栈底：固定的，不允许进行插入和删除的一端。

特点：后进先出（LIFO）

数学性质：n个不同元素进栈，出栈元素不同排列的个数为$\frac{1}{n+1} \mathrm{C}_{2n}^{n} $(卡特兰树)​

基本操作

InitStack(&S);			//初始化一个空栈S
DestoryList(&S);		//销毁栈，并释放栈S所占用的存储空间

Push(&S,x);				//进栈，若栈S未满，则将x加入使之成为新栈顶
Pop(&S,&x);				//出栈，若栈非空，则弹出栈顶元素，并用x返回

GetTop(S,&x);			//读栈顶元素，若栈S非空，则用x返回栈顶元素

StackEmpty(S);			//判断一个栈S是否为空。若S为空，则返回true,否则返回false

顺序栈

顺序栈的实现

采用顺序存储的栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时设一个指针指示当前栈顶元素的位置。

#define MaxSize 10		//定义栈中元素的最大个数
typedef struct{
    Elemtype data[MaxSize];		//存放栈中元素
    int top;				   //栈顶指针
}SqStack;

栈顶指针：\(S.top\)​，初始设置为\(S.top=-1\);栈顶元素：\(S.data[S.top]\)

顺序栈的基本运算

//初始化
void InitStack(SqStack& S)
{
    S.top=-1;
}

//判断空
bool InitStack(SqStack S)
{
    if(S.top=-1)
        return true;
    return false;
}

//进栈
//栈不满时，栈顶指针先加1，再送值到栈顶元素
bool Push(SqStack& S,Elemtype x)
{
    if(S.top==MaxSize-1)
        return false;
    S.data[++S.top]=x;
    return true;
}

// 出栈
// 栈非空时，先取栈顶元素值，再将栈顶指针减1
bool Pop(SqStack& S,Elemtype& x)
{
    if(S.top==-1)
        return false;
    e=S.data[S.top--];
    return true;
}

//取栈顶元素
bool GetTop(SqStack S,Elemtype& x)
{
    if(S.top==-1)
        return false;
    e=S.data[S.top];
    return true;
}

共享栈

将两个顺序栈共享一个一维数组空间

image-20210811213129939

链栈

链栈的实现

采用链式存储；

优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。

通常采用单链表实现，并规定所有操作都是在单链表的表头进行。(Lhead指向栈顶元素)

typedef struct Linknode{
    Elemtype data;
    struct Linknode *next;
}*LiStack;

具体操作自己实现

栈的应用

括号匹配

算法思想：

  1. 初始设置一个空栈，顺序读入括号
  2. 若是右括号，则使置于栈顶的最急迫期待的左括号进行匹配，或者不合法的i情况（不匹配，退出程序）
  3. 若是左括号，则压入栈中；算法结束时，栈为空，否则括号序列不匹配

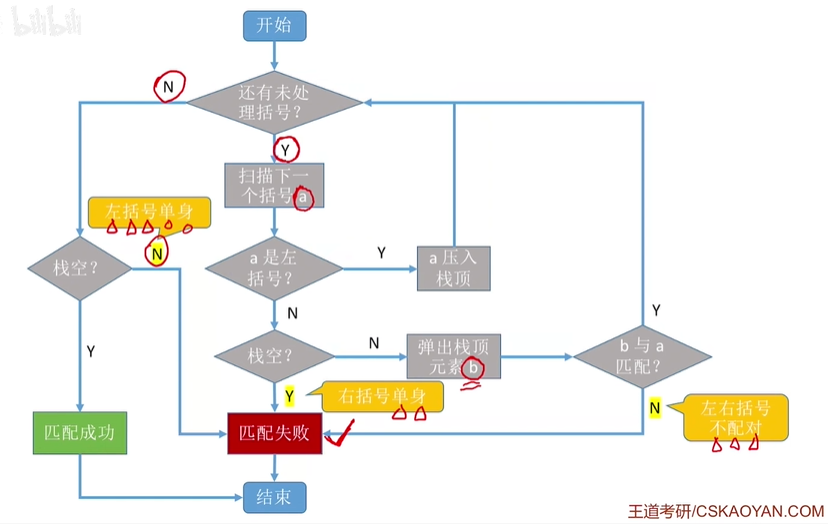
image-20210811231653080

//代码实现
bool bracketCheck(char str[],int length)
{
    SqStack S;
    InitStack(S);
    for(int i=0;i<length;i++)
    {
        if(str[i]=='('||str[i]=='['||str[i]=='{')
            Push(S,str[i]);
        else
        {
            if(StackEmpty(S))
                return false;
            char topElem;
            Pop(S,topElem);
            if(str[i]==')'&&topElem!='(')
                return false;
            if(str[i]==']'&&topElem!='[')
                return false;
            if(str[i]=='}'&&topElem!='{')
                return false;
        }
    }
    return StackEmpty(S);
}

表达式求值

中，后，前缀表达式

image-20210811232353371

手算

中缀转后缀手算方法：

  1. 确定中缀表达式中的各个运算的运算顺序
  2. 选择下一个运算符，按照【左操作数，右操作数，运算符】的方式组合成一个新的操作数
  3. 如果还有运算符没被处理，就继续②

“左优先”原则：只要左边的运算符能先计算，就优先算左边的(保证手算和机算的结果一样)

后缀表达式的手算方法：从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数（注意：两个操作数的左右顺序）

特点：最后出现的操作数先被运算

用栈实现后缀表达式的计算

  1. 从左往右扫描下一个元素，直至处理完所有元素
  2. 若扫描到操作数则压入栈，并回到①；否则执行③
  3. 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①

注意：先出栈的是”右操作数“

中缀转前缀的手算方法：

  1. 确定中缀表达式中各个运算符的运算顺序
  2. 选择下一个运算符，按照【运算符，左操作数，右操作数】的方式组合成一个新的操作数
  3. 如果还有运算符没被处理，就继续②

“右优先”原则：只要右边的运算符能先计算，就优先算右边的

用栈实现前缀表达式的计算

  1. 从右往左扫描下一个元素，直至处理完所有元素
  2. 若扫描到操作数则压入栈，并回到①；否则执行③
  3. 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①

注意：先出栈的是”左操作数“

机算

中缀转后缀表达式

初始化一个栈，用于保存暂时还不能确定运算顺序的运算符

从左到右处理各个元素，直到末尾，可能遇到三种情况：

  1. 遇到操作数，直接加入后缀表达式
  2. 遇到界限符。遇到“（”直接入栈；遇到“）”则依次弹出栈内运算符并加入后缀表达式，直至弹出“（”为止。注意：“（”不加入后缀表达式
  3. 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到“（”或栈空则停止。之后再把当前运算符入栈。

按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

中缀表达式的计算

用栈实现：初始化两个栈，操作数栈和运算符栈

  1. 若扫描到操作数，压入操作数栈
  2. 若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈）

递归的应用

函数调用背后的过程

函数调用的特点：最后被调用的函数最先执行结束（LIFO）

函数调用时需要一个栈存储：

  • 调用返回地址
  • 实参
  • 局部变量

递归调用时，函数调用栈可称为“递归调用栈”

每进入一层递归，就将递归调用所需信息压入栈顶

每退出一层递归，就从栈顶弹出相应信息

适合用“递归”算法解决：可以把原始问题转换为属性相同，但规模较小的问题。如：斐波那契数列

队列

基本概念

队列是只允许在一端进行插入，在另一端删除的线性表。

特点：先进先出（FIFO）

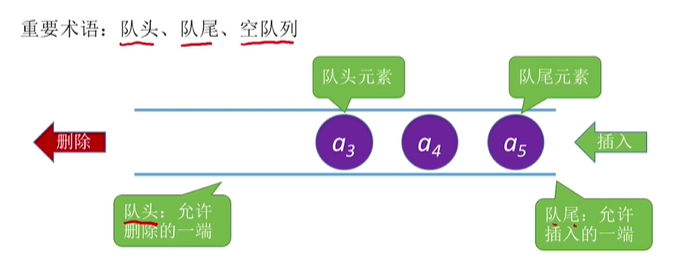
image-20210811213958995

基本操作

InitQueue(&Q);			//初始化队列，构造一个空队列Q
DestoryQueue(&Q);		//销毁队列。销毁并释放队列Q所占的内存空间

EnQueue(&Q,x);			//入队，若队列未满，将x加入，使之成为新的队尾
DeQueue(&Q,&x);			//出队，若队列Q非空，删除队头元素，并用x返回

GetHead(Q,&x);			//读队头元素，若队列Q非空，则将队头元素赋值给x

QueueEmpty(Q);			//判队列空，若队列Q为空返回true,否则返回false

队列的顺序存储结构

队列的顺序存储

#define MaxSize 50				//定义队列中元素的最大个数
typedef struct{
    Elemetype data[Maxsize];	//存放队列元素
    int front,rear;				//队头指针和队尾指针
}

初始状态（队空条件）：\(Q.front=Q.rear=0\)

进队操作：队不满时，先送值到队尾元素，再将队尾指针加1

出队操作：队不空时，先取队头元素值，再将队头指针加1

“上溢出”（加溢出）：\(Q.rear=MaxSize\)

具体操作代码自己实现

循环队列

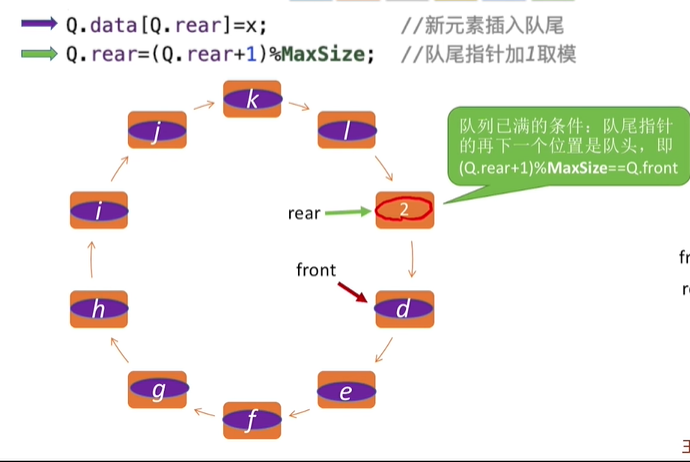
image-20210811220856173

初始时：\(Q.front=Q.rear=0\)

队首指针进1：\(Q.front=(Q.front+1)\%Maxsize\)​

队尾指针进1：\(Q.rear=(Q.rear+1)\%Maxsize\)​

队列长度：\((Q.rear+Maxsize-Q.front)\% MaxSize\)

判断判空判满方法

  • 牺牲一个存储单元区分队空和队满

    队满条件：\((Q.rear+1)\%MaxSize==Q.front\)

    队空条件仍为：\(Q.rear=Q.front\)

    队列中元素个数：\((Q.rear-Q.front+MaxSize) \% MaxSize\)

  • 增加一个\(Size\)变量记录队列长度

    队满条件：\(Q.Size=MaxSize\)​

    队空条件仍为：\(Q.Size=0\)

  • 增加\(tag=0/1\)标记出队/入队

    \(tag=0\)​​时,\(Q.front=Q.rear\)​​，则为队空（出队操作）

    \(tag=1\)​时,\(Q.front=Q.rear\)​​，则为队满（入队操作）

具体操作代码自己实现

队列的链式存储结构

队列的链式存储结构

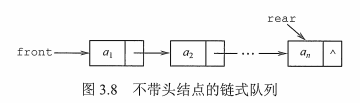
image-20210811222426505

typedef struct{    Elemtype data;    struct LinkNode *next;}LinkNode;typedef struct{					//链式队列    LinkNode *front,*rear;		//队列的队头和队尾指针}LinkQueue;

链式队列的基本操作

以下代码都是带头结点，若不带头结点则需要进行特殊处理（自己思考）

//初始化void InitQueue(LinkQueue &Q){    Q.front=Q,rear=(LinkNode*)malloc(sizeof(LinkNode));    Q->front->next=NULL;}

//判队空bool Isempty(LinkQueue Q){    if(Q.front==Q.rear)         return true;    return false;}

//入队Void EnQueue(LinkQueue &Q,Elemtype x){    LinkNode *s=(LinkNode*)malloc(sizeof(LinkNode));    s->data=x;s->next=NULL;    Q.rear->next=s;    Q.rear=s;}

//出队bool DeQueue(LinkQueue &Q,Elemtype &x){    if(Q.front==Q.rear)         return false;    LinkNode* p=Q.front->next;    x=p->data;    Q.front->next=p->next;    if(Q.rear==p)        Q.rear==Q.front;			//若原队列中只有一个结点，删除后变空    free(p);    return true;    }

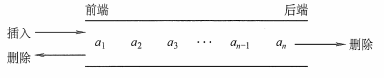
双端队列

双端队列时指允许两端都可以进行入队和出队操作的队列。

image-20210811231000563

输出受限的双端队列：允许在一端进行插入和删除，但在另一端只允许插入的双端队列

image-20210811231050883

输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列

image-20210811231108551

考点：输出序列

队列的应用

树的层次遍历

  1. 根结点入队
  2. 若队空（所有结点都已处理完毕），则结束遍历；否则重复③操作
  3. 队列中第一个结点，并访问之。若其有左孩子，则将左孩子入队；若其有右孩子，则将右孩子入队，返回②。

操作系统的应用

image-20210812230736074

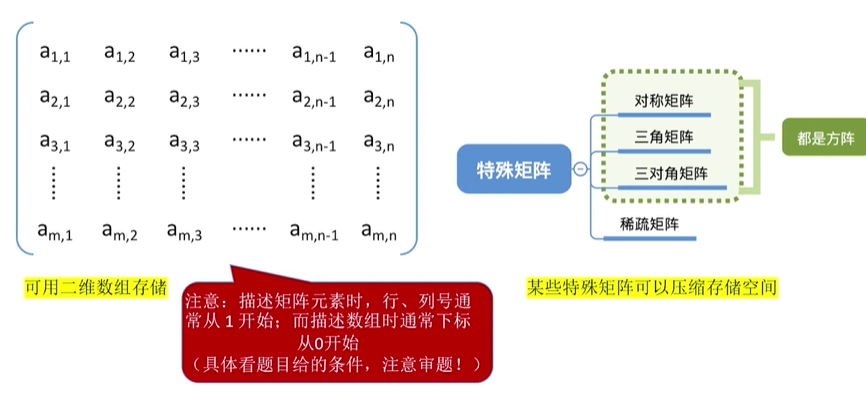
特殊矩阵的压缩存储

一维数组的存储结构

image-20210812230915595

二维数组的存储结构

image-20210812231018387

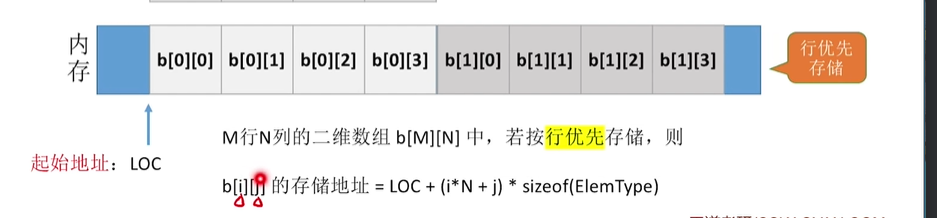
image-20210812231113743

image-20210812231146158

普通矩阵的存储

image-20210812231231304

对称矩阵

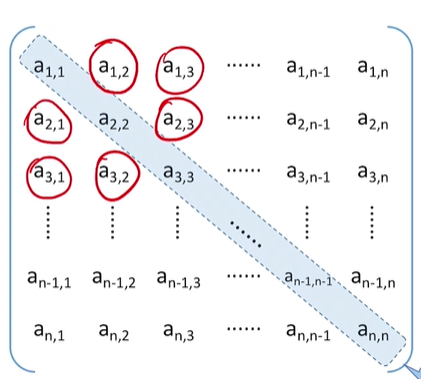
image-20210812231932513

若n阶方阵中任意一个元素\(a_{i，j}\)​都有\(a_{i,j}=a_{j,i}\)，则该矩阵为对称矩阵。

策略：只存储主对角线+下三角区

按行优先原则将各元素存入一维数组中（长度:\((1/n)*n/2\)）

按照行优先原则，元素下标之间的对应关系如下：

\[\begin{equation} k=\left\{ \begin{array}{rcl} \frac {i(i-1)}{2}+j-1 & & i\ge j(下三角区和主对角元素)\\ \frac {j(j-1)}{2}+i-1 & & j\ge i(上三角区和主对角元素) \end{array} \right. \end{equation} \]

三角矩阵

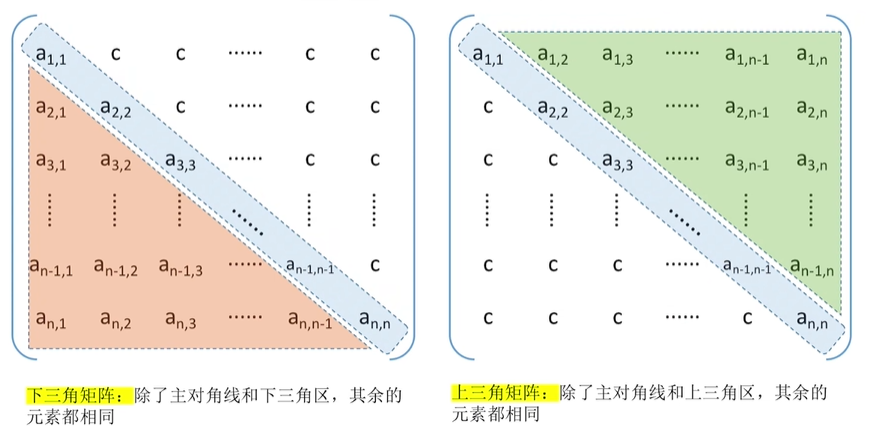
image-20210812232303586

压缩存储策略：按行优先原则则将橙色区元素存入一维数组，并在最后一个位置存储常量c句号

(下三角矩阵)元素下标之间的对应关系如下：

\[\begin{equation} k=\left\{ \begin{array}{rcl} \frac {i(i-1)}{2}+j-1 & & i\ge j(下三角区和主对角元素)\\ \frac {n(n+1)}{2} & & i< j(上三角区) \end{array} \right. \end{equation} \]

(上三角矩阵)元素下标之间的对应关系如下：

\[\begin{equation} k=\left\{ \begin{array}{rcl} \frac {(i-1)(2n-i+2)}{2}+j-1 & & i\le j(上三角区和主对角元素)\\ \frac {n(n+1)}{2} & & i> j(下三角区) \end{array} \right. \end{equation} \]

三对角矩阵

image-20210812232715400

三对角矩阵，又称带状矩阵；

当\(|i-j|>1\)时，有\(a_{i,j}=0(i\le i,j \le n)\)

压缩存储策略：按行（列）优先原则，只存储带状部分（长度为：\(3n-2\)）

按行优先原则，对应关系\(k=2i+j-1\),\(\lceil(k+2)/3 \rceil\)或者\((\lfloor (k+2)/3+1 \rfloor)\)

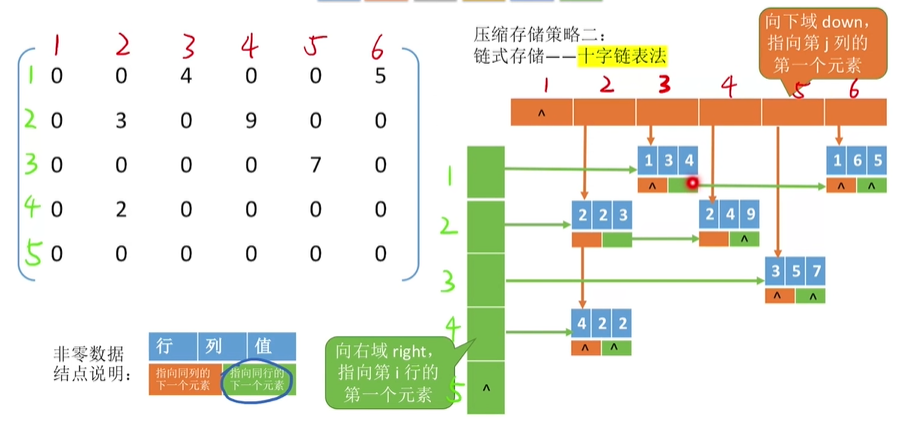
稀疏矩阵

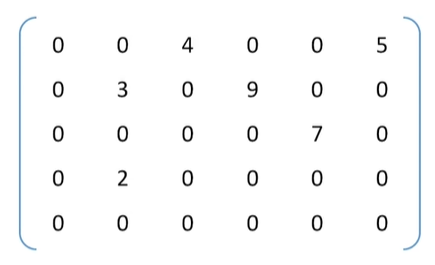
image-20210812233222010

非零元素远远少于矩阵元素的个数

压缩存储策略：

  • 顺序存储-三元组<行，列，值>

  • 链式存储-十字链表法

    image-20210812233414567

posted @ 2021-08-26 17:09  Ligo丶  阅读(656)  评论(0)  编辑  收藏  举报