计算机组成原理笔记2-数制、字符、校验码、定点数、浮点数、算术逻辑单元

目录

• 数制
  • 进制转换
  • BCD码*
• 字符
• 校验码*
  • 奇偶校验码
  • 海明码
  • 循环冗余校验码(CRC码 )
• 定点数的表示
  • 无符号数
  • 有符号数
    • 原码
    • 补码
    • 反码
    • 移码
• 定点数的运算
  • 移位运算
    • 逻辑移位
    • 算术移位
    • 循环移位
  • 加减运算
    • 原码的加减运算
    • 补码的加减运算
  • 溢出判断
  • 符号扩展
  • 乘法运算
    • 原码一位乘法
    • 补码一位乘法
    • 原码两位乘法*
  • 除法运算
    • 原码恢复余数法
    • 原码不恢复余数法(原码加减交替法)
    • 补码不恢复余数法(补码加减交替法)
  • 强制类型转换
  • 数据的存储和排列
• 浮点数的表示
  • 浮点数的规格化
  • 规格化浮点数的特点
  • 浮点数表示范围
  • IEEE 754标准
• 浮点数的运算
  • 加减运算
  • 强制类型转换
• 算术逻辑单元
  • ALU
    • 功能
    • 基本结构
  • 加法器
    • 一位全加器
    • 串行加法器
    • 并行加法器

数制

进制转换

BCD码*

• 8421BCD码:映射关系如下

  0	1	2	3	4	5	6	7	8	9
  0000	0001	0010	0011	0100	0101	0110	0111	1000	1001

  4位二进制-->16种不同的状态

  BCD码只使用其中10种-->不同的映射方案

• 余3码:8421码+(0011)

  0	1	2	3	4	5	6	7	8	9
  0011	0100	0101	0110	0111	1000	1001	1010	1011	1100

• 2421码:改变权值定义

  0	1	2	3	4	5	6	7	8	9
  0000	0001	0010	0011	0100	1011	1100	1101	1110	1111

字符

1. ASCII码:共128个字符

   可印刷字符:32~126 数字:48~57 大写字母:65~90 小写字母:97~122

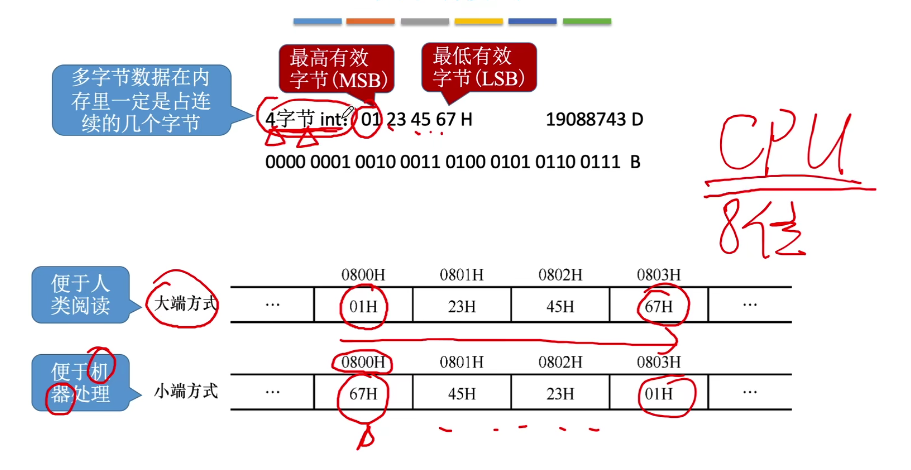
2. 大小端模式:

   大端模式:存储单元内先存储高位字节,后存储低位字节的顺序

   小段模式:存储单元内先存储低位字节,后存储高位字节的顺序

3. 汉字的表示和编码:

   GB 2312-80:汉字+各种符号共7445个

校验码*

码距:两个合法码字对应位上数字的不同位的个数(码距大于1可以检测错误)

奇偶校验码

只能检测出奇数位错误

奇校验码:整个校验码(有效信息位和校验位)中"1"的个数为奇数

偶校验码:整个校验码(有效信息位和校验位)中"1"的个数为偶数

海明码

是一种有多位校验码,具有检测并纠正以为错误代码的纠错码.(注意一下大小端表示)

设计思路:分组校验-->多个校验位-->校验位标注出错位置

求解步骤:

1. 确定海明码的位数:

   \[2^k \ge n+k+1 \]

   n为信息位数,k为校验位数,满足上式不等式的最小k即为校验位数

   下面是一些n与k的关系表格

   ​

   n	1	2-4	5-11	12-16	27-57	58-120
   k	2	3	4	5	6	7

   如:信息位为1010-->海明码的位数即为3位

2. 确定校验位的分布

   校验位Pi放在海明位号为2^(i-1)的位置上

   信息位按顺序放到其余位置

   如:上面1010中,信息位为4位(D₄D₃D₂D₁),而检验码位为3位(P₃P₂P₁),对应海明码为H₇H₆H₅H₄H₃H₂H₁,对应关系如下图:

   H7	H6	H5	H4	H3	H2	H1
   D4	D3	D2	P3	D1	P2	P1

3. 求校验位的值

   • 把放信息位置的位置的下标序号转换为对应海明码位数的二进制

   • 每一位中为1的那个位置中的信息位进行异得到即为校验码中该位的值(所以要校验的位异或为0)

   如:H₃:3-->011 H₅:5-->101 H₆:6-->110 H₇:7-->111

   \[P_1=H_3 \oplus H_5 \oplus H_7=D_1 \oplus D_2 \oplus D_4=0 \oplus 1 \oplus 1 =0 \]
   \[P_2=H_3 \oplus H_6 \oplus H_7=D_1 \oplus D_3 \oplus D_4=0 \oplus 0 \oplus 1 =1 \]
   \[P_1=H_5 \oplus H_6 \oplus H_7=D_2 \oplus D_3 \oplus D_4=1 \oplus 0 \oplus 1 =0 \]

4. 纠错

   把求出的校验位的值与第三步中的求校验位公式再进行异或操作(令所以要校验的位异或运算)

   如过全都为零就是没有出错;如果不是零就表示海明码中出错位置,将其取反就可以起到纠错功能

   如:

   \[S_1=P_1 \oplus D_1 \oplus D_2 \oplus D_4=0 \oplus 0 \oplus 1 \oplus 1=0 \]
   \[S_2=P_2 \oplus D_1 \oplus D_3 \oplus D_4=1 \oplus 0 \oplus 0 \oplus 1=0 \]
   \[S_3=P_3 \oplus D_2 \oplus D_3 \oplus D_4=0 \oplus 1 \oplus 0 \oplus 1=0 \]

   将S₃S₂S₁(000)组合即可得得到出错的位置

循环冗余校验码(CRC码 )

信息位	校验位
K位	R位

1. 确定K丶R以及生成多项式对应的二进制码
2. 移位:信息码左移R位,地位补0
3. 相除:对移位后的信息码,用生成多项式进行模2除法,产生余数
4. 检错和纠错:接受后的信息码用生成多项式进行模2除法,若余数为零,则没有错误;若余数为其余,则有错误

定点数的表示

无符号数

整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值

n位的无符号数表示范围:0~\(2^{n-1}\)

有符号数

小数点:隐含存储(定点数:事先约定)

定点小数: 表示范围 \(-(1-2^{-n})\)~\(1-2^{-n}\) , n为尾数位数

定点整数: 表示范围:

​ 绝对值:0~2ⁿ-1

​ 有n位尾数的定点整数:-(2ⁿ-1)~2ⁿ-1

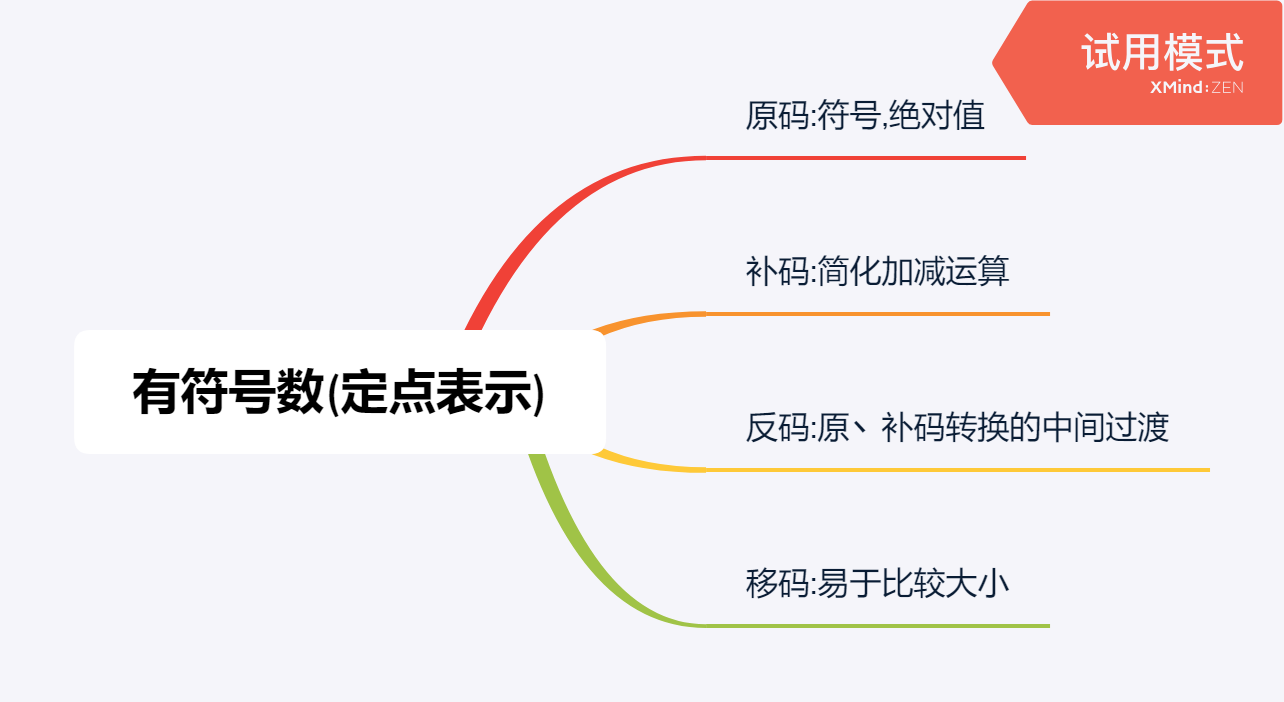
原码

纯整数原码:

\[\begin{equation}[x]_原=\left\{\begin{aligned} 0,x && 2^n>x\ge0\\2^n-x=2^n+ \vert x \vert && 0\ge x>-2^n\\\end{aligned}\right.\end{equation} \]

​ 若字长为n+1,则原码的表示范围为

\[-(2^n-1) \le x \le 2^n-1 (关于原点对称) \]

​ 纯小数原码:

\[\begin{equation} [x]_原=\left\{ \begin{aligned} x && 1>x\ge0\\ 1-x=1+ \vert x \vert && 0\ge x>-1\\ \end{aligned} \right. \end{equation} \]

​ 若字长为n+1,则原码的表示范围为

\[-(1-2^n) \le x \le 1-2^n (关于原点对称) \]

补码

正数:补码与原码的表示相同.[x]补=[x]原

负数:原码符号位不变,数值部分按位取反,末位加1(取反加1)

​ 此规则同样适用于由补码求原码

纯整数补码:

\[\begin{equation}[x]_补=\left\{\begin{aligned} 0,x && 2^n>x\ge0\\ 2^{n+1}+x=2^{n+1}- \vert x \vert && 0\ge x\ge-2^n\\\end{aligned}\right.\end{equation} \]

​ 若字长为n+1,则补码的表示范围为 (比原码多表示-2ⁿ )

\[-2^n \leq x \leq 2^n-1 \]

\[[-2^n]_补=100000-10000=10000 \]

​ 纯小数补码:

\[\begin{equation} [x]_补=\left\{ \begin{aligned} x && 1>x\ge0\\ 2+x=2- \vert x \vert && 0>x \ge -1\\ \end{aligned} \right. \end{equation} \]

​ 若字长为n+1,则补码的表示范围为 (比原码多表示-1)

\[-1 \leq x \leq 1-2^n \]

\[[-1]_补=10.0000-1.0000=1.0000 \]

反码

正数:反码与原码表示相同,[x]_补=[x]_原

负数:原码符号位不变,数值部分按位取反。

​ 此规则同样适用于由反码求原码

纯整数反码:

\[\begin{equation}[x]_反=\left\{\begin{aligned} 0,x && 2^n>x\ge0\\(2^{n+1}-1)+x&& 0\ge x>-2^n\\\end{aligned}\right.\end{equation} \]

​ 若字长为n+1,则反码的表示范围为

\[-(2^n-1) \le x \le 2^n-1 (关于原点对称) \]

​ 纯小数反码:

\[\begin{equation} [x]_反=\left\{ \begin{aligned} x && 1>x\ge0\\ (2-2^{-n})+x && 0\ge x>-1\\ \end{aligned} \right. \end{equation} \]

​ 若字长为n+1,则反码的表示范围为

\[-(1-2^n) \le x \le 1-2^n (关于原点对称) \]

​ 原补反的相互转换:

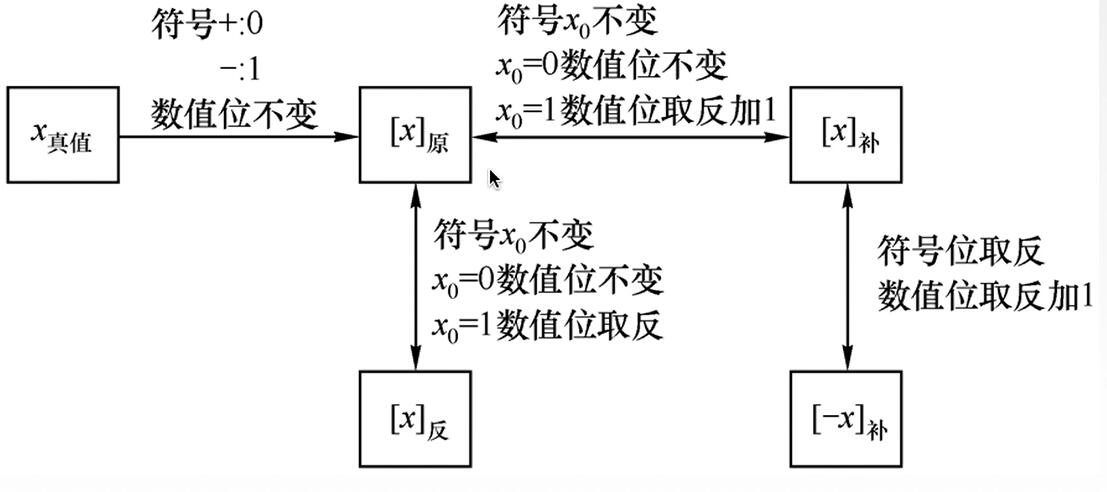
移码

在真值X上加上一个常数(偏置值),通常这个常数取2ⁿ

\[[x]_移=2^n+x \]

​ 移码求真值:

• 转换为无符号数真值,然后减去偏置值对应的无符号数真值得到移码
• 先转换为补码(符号位取反),再转换为真值

定点数的运算

移位运算

逻辑移位

机器采用无符号数

逻辑移位:逻辑左移时,高位移丢,低位添0;逻辑右移,低位移丢高位添0。

算术移位

机器采用有符号数

左移相当于乘以基数,右移相当于除以基数

算术移位的填补规则

	码制	添补代码
正数	原码、补码、反码	0
负数	原码	0
	补码	左移添0
		右移添1
	反码	1

原码算术移位:左移丢1,运算出错;右移丢1,影响精度。

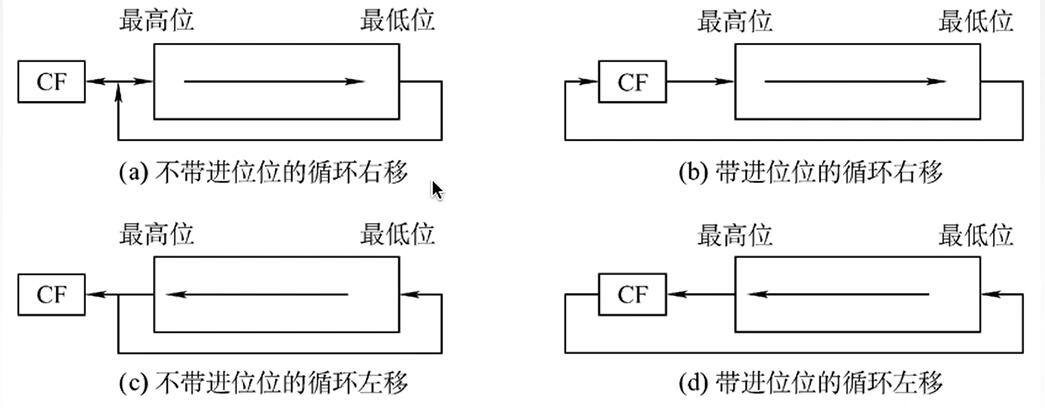
循环移位

高位移出到低位,低位移出到高位。

循环移位规则如下:

加减运算

原码的加减运算

加法运算:

• 同号：绝对值相加，符号位不变（可能回溢出）
• 异号：绝对值大的减绝对值小的，符号位同绝对值大的数

减法运算：“减数”符号取反，转变为加法

补码的加减运算

基本思路:

1. 转换为x+y的形式
2. 计算[x]_补+[y]_补

溢出判断

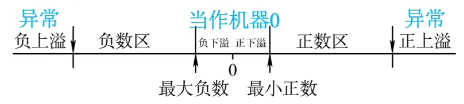
上溢(正溢出):两个数相加的结果超过了数据类型所能表示的最大范围，结果为负数

下溢(负溢出):两个数相加的结果超过了数据类型所能表示的最小范围，结果为正数（包括0）

方法一:采用一位符号位

设A的符号为A_s,B的符号为B_s,运算结果的符号为S_s,则溢出逻辑表达式为

\[V=A_sB_s \bar S_s+ \bar A_s \bar B_sS_s \]

若V=0,表示无溢出;若V=1,表示有溢出。

方法二:采用一位符号位,根据数据位进位情况判断溢出

	符号位的进位Cs	最高数位的进位C1
正溢出	0	1
负溢出	1	0

即:C_s>与C₁不同时有溢出

溢出逻辑判断表达式为

\[V=C_s \oplus C_1 \]

若V=0,表示无溢出;V=1,表示有溢出。

方法三:采用双符号位

正数符号为00,负数符号为11

记两个符号为S_s1S_s2,则

\[V=S_{s1} \oplus S_{s2} \]

若V=0,表示无溢出;V=1,表示有溢出。

若符号为01,则表示运算结果大于允许取值访问的最大整数.称为正溢出;若符号为10,则表示表示运算结果小于允许取值访问的最小整数.称为负溢出。

采用双符号位的移位运算:低位符号位参与移位,高位符号位代表真正的符号

符号扩展

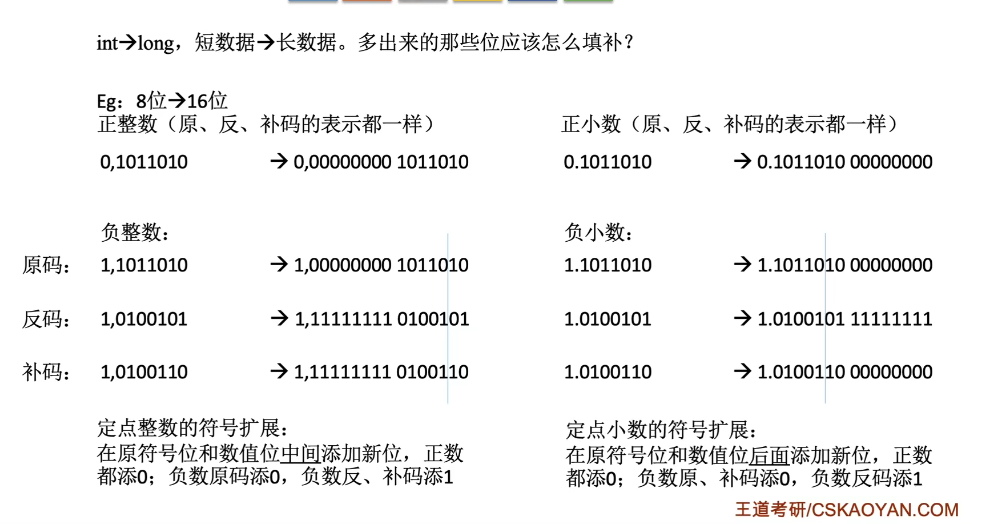
定点整数的符号扩展：

在原符号位和数值位中间添加新位

• 正数都添0
• 负数原码添0；负数反，补码添1

定点小数的符号扩展：

在原符号位和数值位后面添加新位

• 正数都添0
• 负数原，补码添0；负数反添1

乘法运算

原码一位乘和补码一位乘都遵循以下规则

1. 多余进位舍去
2. 一直执行到乘数被用完(被移出完)
3. 原码最后需要移位,补码不需要移位
4. 原码补码一位乘取值都不去原乘数的数

原码一位乘法

符号位

绝对值

定义:符号位单独参与运算,数据位取绝对值,每次将一位乘数对应的部分积与原部分积的累加和进行相加,并右移一位(逻辑移位),直到乘数的所有位被用完。

符号位:

\[符号位=x_s \oplus y_s \]

例题:设机器字长为5位(含一位符合位,n=4),x=-0.1101,y=+0.1011,采用原码一位乘法求x*y

符号:一正一负,结果为负

\(|x|=00.1101,|y|=00.1011\)

首先累加寄存器(ACC)存放机器字长个零,乘商寄存器(MQ)存放乘数1011

ACC	MQ
00000	1011

因为MQ的尾数为1,所以ACC加上被乘数1101(下面表格第二行)

然后再右移一位,，ACC的低位移到MQ,移出的位1舍去(下面表格第三行)

ACC	MQ
01101	1011
00110	1101

又因为MQ的尾数为1,所以ACC加上被乘数1101

然后再右移一位,ACC的低位移到MQ，移出的位1舍去

ACC	MQ
10011	1101
01001	1110

因为此时MQ中的尾数,所以ACC加上0000

然后再右移一位,ACC的低位移到MQ，移出的位0舍去

ACC	MQ
01001	1110
00100	1111

又因为MQ的尾数为1,所以ACC加上被乘数1101

然后再右移一位,移出的位1舍去

ACC	MQ
10001	1111
01000	1111

此时乘数1011已被完全移出,即可得到结果01000111

所以最后的结果为\(x*y=-0.1000111\)

手算结果

补码一位乘法

补码一位乘在操作和判断位上和原码一位乘有区别（原码一位乘为一位，补码一位乘为两位)(移位：补码的算术右移) ;具体操作与原码相同

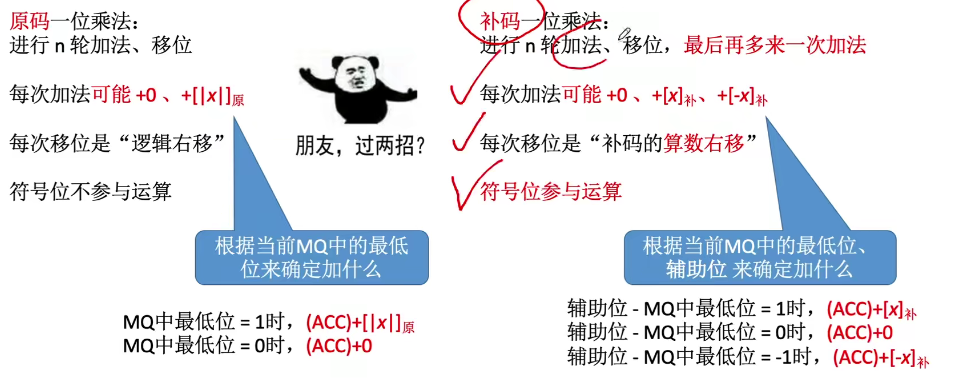
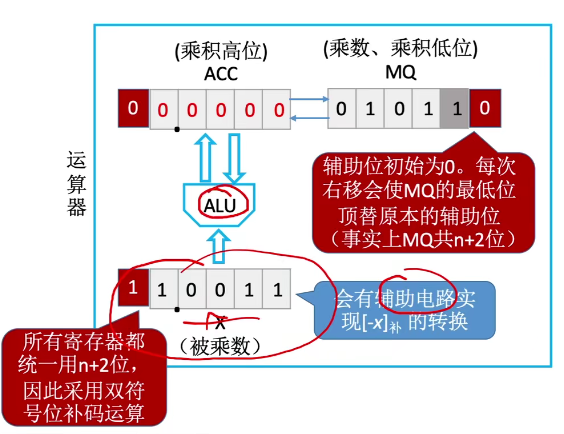
并且操作和判断位遵循以下规则:

Yn(高位)	Yn+1低位)	操作
0	0	部分积右移一位
0	1	部分积加\([被乘数x]_补\),右移一位
1	0	部分积加\([-被乘数x]_补\),右移一位
1	1	部分积右移一位

根据Y_n+1-Y_n判断:

• Y_n+1-Y_n=0,加0,右移一位
• Y_n+1-Y_n=1,加[被乘数x]_补,右移一位
• Y_n+1-Y_n=-1,加[-被乘数x]_补,右移一位

手算结果

原码两位乘法*

讨论x*y=z

1. 原码两位乘法与原码一位乘法一样,符号位不参与运算(即符号位进行异或运算)

2. 部分积和被乘数x均采用三位符号,乘数y末位每次要加一个c,c一开始是0

3. 根据以下规则进行运算:

   此处的右移为算术右移

   乘数最后三位	操作
   000	部分积加0,右移两位,c变为0
   001	部分积加|x|,右移两位,c变为0
   010	部分积加|x|,右移两位,c变为0
   011	部分积加2|x|,右移两位,c变为0
   100	部分积加2|x|,右移两位,c变为0
   101	部分积减|x|,右移两位,c变为1
   110	部分积减|x|,右移两位,c变为1
   111	部分积加0,右移两位,c变为1

4. 重复上面的步骤3直到乘数为00.0

5. 而乘数y用双符号位还是单符号表示根据乘数y的数值的奇偶性判断,而且最后一步移位与否也与乘数y的数值的奇偶性有关:

   • 如果乘数y的尾数的位数为偶数,则乘数y用双符号表示,最后一步不移位。
   • 如果乘数y的尾数的位数为奇数,则乘数y用单符号表示,最后一步要移一位。

除法运算

符号位

绝对值

符号位和数值位分开处理

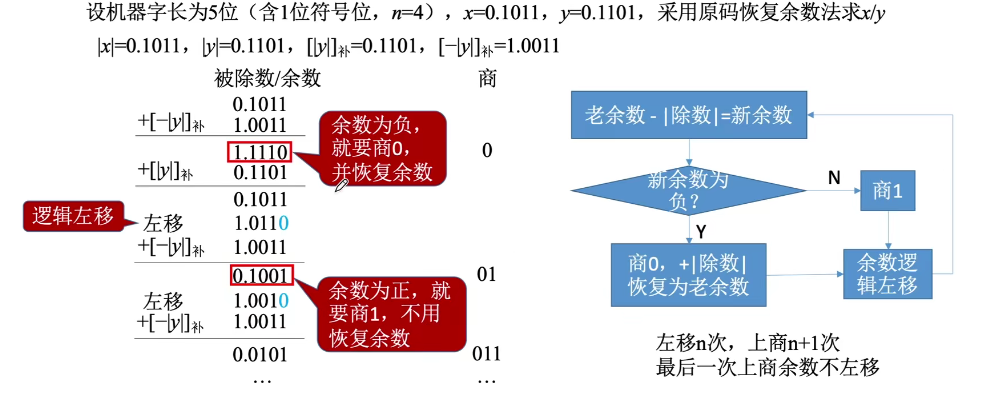
原码恢复余数法

具有n位尾数的合法除法,需要逻辑移位n次,上商n+1次。

步骤:

1. 符号位单独处理(异或运算),分别取除数和被除数绝对值进行运算。

2. 若余数(被除数)为正,表示够减,商上1,左移一位,加上\([-y]_补\);

   若余数(被除数)为负,表示不够减,商上0,恢复余数(加上除数\([y]_补\)),左移一位,加上\([-y]_补\)

3. 重复上一步骤n次。

4. 若最后一步余数为负,需要恢复余数（加上\([-y]_补\)）,否则不需要。

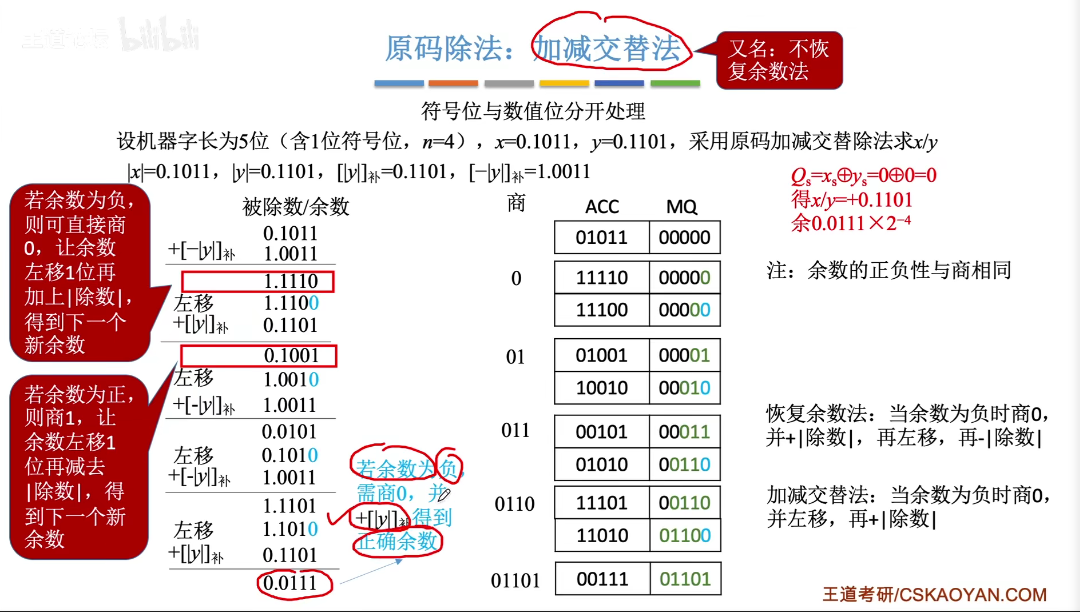
原码不恢复余数法(原码加减交替法)

具体步骤与原码不恢复余数法大致一样,区别如下:

若余数(被除数)为负,表示不够减,商上0,恢复余数(加上除数),左移一位,加上[-y]_补,加上[y]_补。(即加上除数)

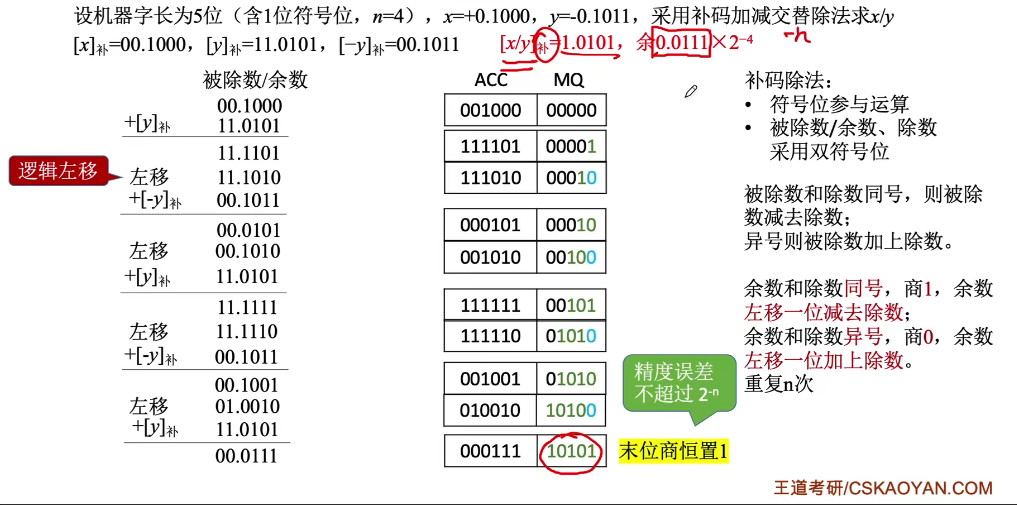
补码不恢复余数法(补码加减交替法)

步骤:

1. 符号位参与运算;若被除数与除数同号,则被除数减去除数;异号则被除数加上除数。

2. 若余数和除数同号,商上1,余数左移一位减去除数(加上\([-y]_补\));（）

   若余数和除数异号,商上0,余数左移一位加上除数(加上\([y]_补\));

3. 重复上一步骤n次。

4. 末位恒置1。

强制类型转换

无符号数与有符号数:不改变数据内容,改变解释方式。

长整数变短整数:高位截断,保留低位。

短整数变长整数:符号扩展。

数据的存储和排列

大小端

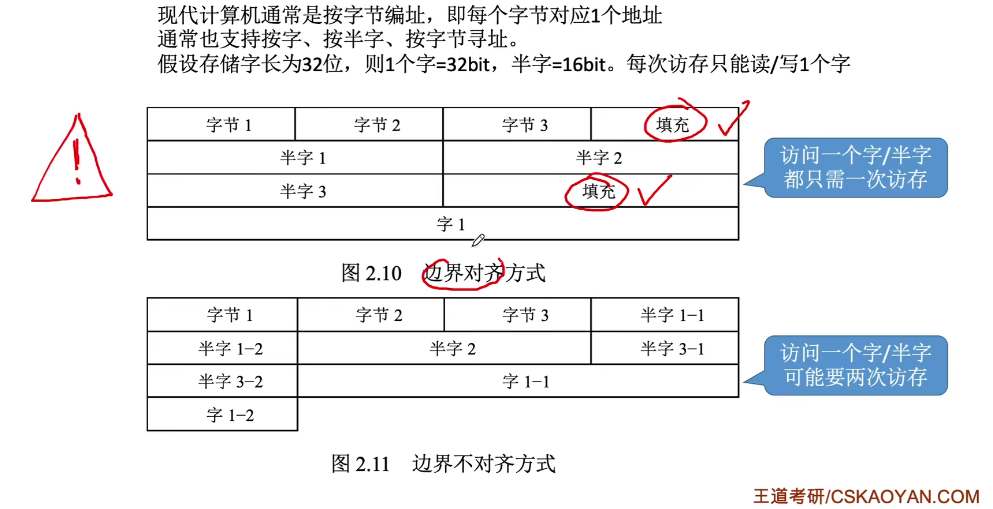
边界对齐

浮点数的表示

Jf	J1J2...Jm	Sf	S1S2...Sn
阶码符号位	阶码数值部分	尾数符号位	尾数数值部分

阶码(E):常用补码或移码表示

尾数(M):常用原码或补码表示

浮点数的真值:

\[N=r^E \times M \]

r为阶码的底,通常为2

阶码E反映浮点数的表示范围及小数点的实际位置;

尾数M的数值部分的位数反映浮点数的精度。

浮点数的规格化

规格化:规定尾数的最高位数必须是一个有效值。

左规:当浮点数运算的结果为非规格化时要进行规格化处理,将尾数左移一位,阶码减1(基数为2时)。

右规:当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数右移一位,阶码加1(基数为2时)。

规范化浮点数的尾数M的绝对值应满足

\[1/r \le \vert M \vert \le 1 \]

如果r=2,则有

\[1/2 \le \vert M \vert \le 1 \]

规格化浮点数的特点

1. 原码规格化后:

   正数为0.1XX...X的形式,其最大值表示为0.11...1;最小值为0.10...0。

   尾数的表示范围为

   \[1/2 \le M \le (1-2^{-n}) \]

   负数为1.1XX...X的形式,其最大值表示为1.10...0;最小值为1.11...1。

   尾数的表示范围为

   \[-(1-2^{-n}) \le M \le -1/2 \]

2. 补码规格化后:

   正数为0.1XX...X的形式,其最大值表示为0.11...1;最小值为0.10...0。

   尾数的表示范围为

   \[1/2 \le M \le (1-2^{-n}) \]

   负数为1.0XX...X的形式,其最大值表示为1.01...1;最小值为1.00...0。

   尾数的表示范围为

   \[-1 \le M \le -(1/2+2^{-n}) \]

当浮点数尾数的基数为2时，原码规格化的尾数最高位一定是1，补码规格化数的尾数最高位一定与尾数符号位相反

当浮点数尾数的基数为4时，原码规格化的尾数最高两位不全为0

当浮点数尾数的基数为8时，原码规格化的尾数最高三位不全为0

浮点数表示范围

IEEE 754标准

ms	E	M
数符	阶码部分,用移码表示	尾数部分,用原码表示(隐藏表示最高位1)

类型	数符	阶码	尾数数值	总位数	偏置值
					十六进制	十进制
短浮点数	1	8	23	32	7FH	127
长浮点数	1	11	52	64	3FFH	1023
临时浮点数	1	15	64	80	3FFFH	16383

阶码的偏置值为：\(2^n-1\)

例如：短浮点数的阶码的偏置值为\(2^8-1=127\)

规格化的短浮点数的真值为:

\[(-1)^s \times 1.M \times 2^{E-127} \]

规格化的长浮点数的真值为:

\[(-1)^s \times 1.M \times 2^{E-1023} \]

一些规定(短浮点数为例):

1. E=0且M=0,则真值为0

2. E=0且M!=0,为非规格化数,真值为

   \[(-1)^s \times 0.M \times 2^{-126} \]

3. 当

   \[1 \le E \le 254 \]

   真值为

   \[(-1)^s \times 1.M \times 2^{E-127} \]

4. E=255（全1）且M!=0时,真值为"NaN"(非数值)

5. E=255（全1）且M=0时,真值为正无穷或负无穷(看符号位)

表示范围:

格式	最小值	最大值
单精度	E=1,M=0:1.0*21-127=2-126	E=254,M=.11...1:1.11...1* 2254-127=2127 *(2-2-23)
双精度	E=1,M=0:1.0*21-1023=2-1022	E=2046,M=.11...1:1.11...1* 22046-1023=21023 *(2-2-52)

由浮点数确定真值（阶码不是全0，也不是全1）

1. 根据“某浮点数”确定数符，阶码，尾数的分布
2. 确定尾数\(1.M\)(注意补充最高的隐含位)
3. 确定阶码的真值=移码-偏移值（可将移码看作无符号数，用无符号数的值减去偏置值）
4. \(-1^s\times 1.M \times 2^{E- 偏移值}\)

浮点数的运算

加减运算

浮点数加减运算步骤:

1. 对阶:使两个数的阶码相等,小阶向大阶看齐,尾数每(算术)右移一位,阶码加1

2. 尾数加减:双符号位方便处理溢出

3. 规格化:

   • 左规：当尾数出现\(00.0\times\times 或者11.1\times \times\)时，需左规，即尾数左移1位，和的阶码减1，直到尾数为\(00.1\times\times 或者11.0\times \times\)
   • 右规：当尾数求和结果溢出（如尾数\(10.0\times\times 或者01.1\times \times\)）需右规，即尾数右移1位，和的阶码加1

4. 舍入:

   • "0"舍"1"入法 :类似于十进制数运算中的"四舍五入"法,即在尾数右移时,被移去的最高位数值位为0,则舍去;被移去的最高数值为1,则在尾数的末位加1。这样做可能会使尾数又溢出,此时需再做一次右规。
   • 恒指置"1"法:尾数右移时,不论丢掉的最高数值位是"1"还是"0",都使右移后的尾数末位横置"1"。这种方法同样使尾数变大和变小的两种可能。

5. 判溢出

   当尾数之和（差）出现\(10.0\times\times 或者01.1\times \times\)时，并不代表溢出，只有奖此数右规后，再根据阶码来判断浮点数运算结果是否溢出。

   • 当阶码符号位出现“01”时：阶码上溢,需要进行中断处理
   • 当阶码符号位出现“10”时：阶码下溢,按机器0处理

强制类型转换

类型	16位机器	32位机器	64位机器
char	8	8	8
short	16	16	16
int	16	32	32
long	32	32	64
long long	64	64	64
float	16	32	32
double	64	64	64

char->int->long->double

float->double

范围丶精度从小到大,转换过程没有损失。

32位

int:表示整数,范围-2³¹~2³¹-1,有效数字32位

float:表示整数及小数,范围正负[2^-126~2¹²⁷(2-2^-23)],有效数字23+1=24位

int->float:可能损失精度

float->int:可能溢出及损失精度

算术逻辑单元

ALU

功能

算术运算:加、减、乘、除等

逻辑运算:与、或、非、异或等

辅助功能:移位、求补等

基本结构

输入、控制、输出

加法器

一位全加器

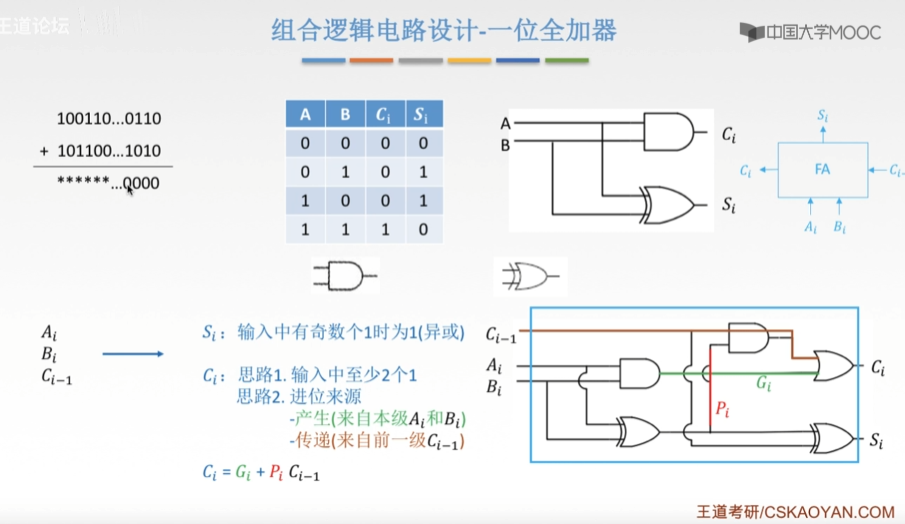
串行加法器

只有一个全加器,数据逐位串行送入加法器中进行运算。进位触发器用来寄存进位信号,以便参与下一场运算。

并行加法器

进位产生原理:进位产生信号&进位传递信号

1. 串行进位的并行加法器

   

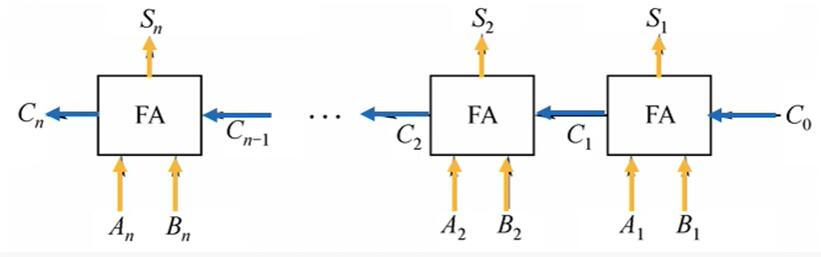
   把n个全加器串接起来,就可进行两个n位数的相加。

   串行进位又称为行波进位,每一级进位直接依赖于前一级的进位,即进位信号是逐级形成的。

2. 并行进位的并行加法器

   

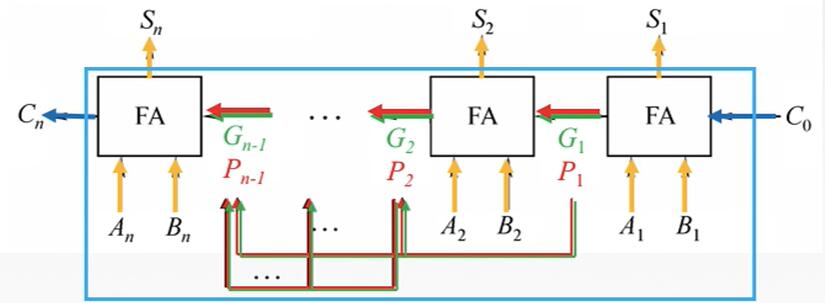
   各级进位信号同时形成,又称为先行进位、同时进位。

   • 单极先行进位方式:组内并行、组间串行进位方式

     

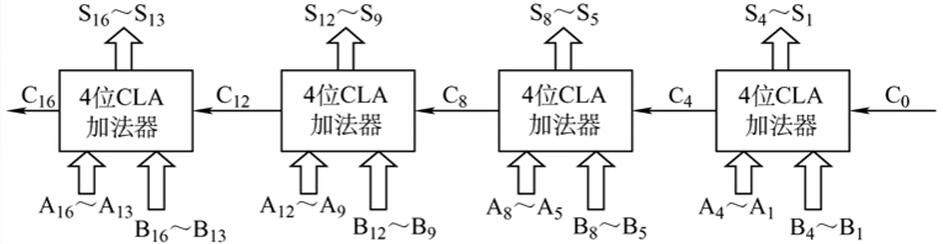
   • 多级先行进位方式:组内并行,组件并行方式

     

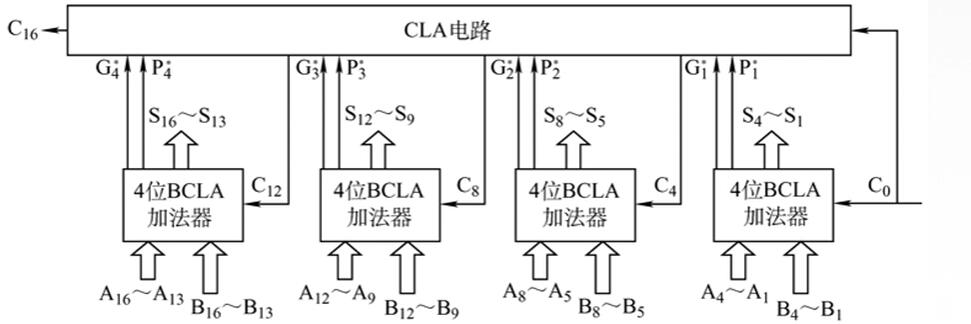
参考:

原码一位乘,补码一位乘:https://www.cnblogs.com/Mayfly-nymph/p/11102136.html

原码两位乘:https://blog.csdn.net/liuchuo/article/details/52922479