7.7集训模拟赛10(虎哥出题怎么能糊呢?!)
我真要吐槽吐槽(原本虎哥出题必不糊,今天是个例外qwq),不知道什么名字就不知道呗,我也不知道啊。
虫子就虫子吧,还有个洞,有洞就有洞吧,这还黑的白的都有,呵呵呵呵
图腾,恩这我知道,图腾你非得计数干嘛,好好当个人不不不好好当个图腾不好吗?以后少计数
啊,十字绣,(秀儿~~~),你就秀去吧~~~
A. 不知道叫什么名字
题目描述

输入格式

输出格式

样例
样例输入
3 1 2 1 2 2 3 3 4 1 1
样例输出
3 2
分析
这道题,倍增+LCA,就ok,但要进行多次判断,要加快读啊,这玩意还卡读入
Code
#include <bits/stdc++.h> using namespace std; const int maxn = 1e6 + 5; struct Edge{ int to, next; }edge[maxn << 1]; int n, m, k, father[maxn][21]; int cnt, head[maxn], dep[maxn]; int read(){//快写 char c=getchar(); int x=0,f=1; while(!isdigit(c)){if(c=='-')f=-1;c=getchar();} while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar(); return x*f; } void write(int a){//快写,呃这到题不用快写应该能过 if(a<0) putchar('-'),a=-a;//不过快读得加啊 if(a>=10)write(a/10); putchar(a%10+48); } void Add(int u, int v){ edge[++cnt].to = v; edge[cnt].next = head[u]; head[u] = cnt; } void Dfs(int rt, int fa){ father[rt][0] = fa; dep[rt] = dep[fa] + 1; for (int i = 1; i <= 20; i++) father[rt][i] = father[father[rt][i-1]][i-1]; for (int i = head[rt]; i; i = edge[i].next){ int v = edge[i].to; if (v != fa){ Dfs(v, rt); } } } void jump(int &u, int &v, int delta){//跳跳跳,跳到同一深度 for (int i = 0; delta; i++){ if(delta & 1) u = father[u][i]; delta >>= 1; } } int Lca(int u, int v){//求LCA if (dep[u] < dep[v]) swap(u, v); jump(u, v, dep[u] - dep[v]); if (u == v) return u; for (int i = 20; i >= 0; i--){ if (father[u][i] != father[v][i]) u = father[u][i], v = father[v][i]; } return father[u][0]; } int main(){ n = read(); m = read(); k = read(); for (int i = 1; i < n; i++){ int u, v; u = read(); v = read(); Add(u, v); Add(v, u); } Dfs(1, 0); for (int i = 1; i <= k; i++){ int d, t; d = read(); t = read(); int LCA = Lca(m, d); if (dep[m] + dep[d] - 2 * dep[LCA] <= t){ m = d; write(d); printf(" "); } else if (dep[m] - dep[LCA] >= t){ jump(m, LCA, t); write(m); printf(" "); } else { jump(d, LCA, dep[m] + dep[d] - 2 * dep[LCA] - t); m = d; write(m); printf(" "); } } }
B. 虫洞
题目描述

输入格式

输出格式

样例
样例输入
4 5 1 0 1 0 10 10 100 10 5 20 15 10 1 2 30 2 3 40 1 3 20 1 4 200 3 4 200
样例输出
130
样例解释

分析
这道题是图论没错,但他黑白会变,(这是什么玩意),所以我们建一个分层图,我们记上层为黑洞,下层为白洞,最一开始都为白洞或黑洞,那我们向黑洞或白洞建边,同时由于会有休息,我们还要自己向自己的另一个颜色的洞建边,若两个洞的颜色不一样,也是如此,然后根据1号节点颜色判断原点,若为白洞spfa(1),否则spfa(1+n)。详细的注释写在代码里。
Code
#include<bits/stdc++.h> using namespace std; const int N = 3e5+10; int n,m; int z[N],w[N],s[N]; int x,y,k; bool vis[N]; int head[N],cnt; int dis[N]; struct edge{//建边 int to; int ne; int w; }e[N*2]; void add(int u,int v,int w){ e[++cnt].to = v; e[cnt].w = w; e[cnt].ne = head[u]; head[u] = cnt; } void spfa(int s){//标准spfa模板 memset(dis,0x3f,sizeof(dis)); queue<int>q; q.push(s); vis[s] = 1; dis[s] = 0; while(!q.empty()){ int f = q.front(); q.pop(); vis[f] = 0; for(int i = head[f];i;i = e[i].ne){ int v = e[i].to; if(dis[v] > dis[f] + e[i].w){ dis[v] = dis[f] + e[i].w; if(!vis[v]){ q.push(v); vis[v] = 1; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i = 1;i <= n;i++)scanf("%d",&z[i]);//状态 for(int i = 1;i <= n;i++)scanf("%d",&w[i]);//质量 for(int i = 1;i <= n;i++)scanf("%d",&s[i]);// for(int i = 1;i <= m;i++){ scanf("%d%d%d",&x,&y,&k); if(z[x] == z[y]){//若同色 add(x,y+n,k);//黑向白建边,注意走到是已经用了一个单位的时间所以走到的那个节点已经变色了 add(x+n,y,k);//白向黑 } else {//若异色 int aa = abs(w[x] - w[y]); add(x+n,y+n,max(0,k-aa));//白向黑 add(x,y,k+aa);//黑向白 } } for(int i = 1;i <= n;i++){//自己向自己的另一个颜色建边,解决停留的问题 add(i,i+n,s[i]); add(i+n,i,0); } if(z[1] == 0)spfa(1+n);//判断起点黑白 else spfa(1); printf("%d\n",min(dis[n],dis[2*n]));//由于最后终点不知黑白,所以取min值 return 0; }
C. 图腾计数
题目描述

输入格式

输出格式

样例
样例输入
5 1 5 3 2 4
样例输出
3 4
数据范围与提示

分析
这道题就是求出一个柱子左侧比他高的,右侧比他高的,左侧比他低的,右侧比他低的,左高x右高即为下凸,左低×右低即为上凸,用暴力一定会超时,所以就用数状数组
Code
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 2e6+10; ll n; ll a[N],c[N]; ll lh[N],ld[N],rh[N],rd[N]; ll lowbit(ll x){ return x & -x; } void updata(ll x,ll k){ while(x<=n){ c[x] += k; x += lowbit(x); } } ll getsum(ll x){ ll sum = 0; while(x){ sum += c[x]; x -= lowbit(x); } return sum; } int main(){ scanf("%d",&n); for(ll i = 1;i <= n;i++){ scanf("%d",&a[i]);//数状数组按照高度为坐标 ld[i] = getsum(a[i]);//求左侧比他低的 lh[i] = i-ld[i]-1;//左高 updata(a[i],1); } memset(c,0,sizeof(c)); for(ll i = n;i >= 1;i--){ rd[i] = getsum(a[i]);//又低 rh[i] = n-i-rd[i];//右高 updata(a[i],1); } ll up=0,down=0; for(ll i = 1;i <= n;i++){ down += lh[i] * rh[i];//下凸 up += ld[i] * rd[i];//上凸 } printf("%lld %lld",down,up);//over return 0; }
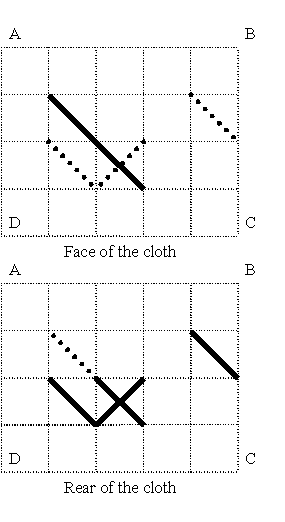
D. 十字绣
题目描述

输入格式

输出格式

样例
样例输入
4 5 ..... .\... ..\.. ..... ..... ....\ .\X.. .....
样例输出
4
数据范围与提示

分析
这这这
我们分析一下,如果一个联通块里有两个正面的线,一个反面的线,那么我们能够推出来这个联通块需要两针才行。在建图的时候,我们把这个字符组成的一个个格子都变成一个点,每个点的标号不同,然后建边
从这个结论可以判断,每一个联通块里的点都有其相对应的最小针数,而这个最小针数就是正面的线和反面的线数量差的绝对值,因为每个边的两个点都会计算,所以最后统计出来的答案应该除以2。
应该注意的一点就是最后如果统计出来的答案是0,我们可以认为是环状,那么应该是有一针的,这里不用除以2,所以直接让ans加2即可
最后需要注意的就是'\'这个符号,直接打出来肯定是不行的,我们可以把它直接放到最后直接else
,也可以'\ \',还有用ASCII码,值为92来判断。
Code
#include<bits/stdc++.h> using namespace std; const int maxn = 1e5+10; struct Node{ int v,next; }e[maxn<<4]; bool vis[maxn],b[maxn]; char s[205][205]; int n,m,a[550][550],z[maxn<<1],num; int ans1,ans2,tot,head[maxn<<1]; void Add(int x,int y,int data){//建边,如果正面就让data为0,这个点的度++,反之则--,我们就在这里求出了答案所需要的绝对值 if(data == 0)z[x]++; else z[x]--; e[++tot].v = y; e[tot].next = head[x]; head[x] = tot; } void Dfs(int x){//深搜找每个联通块的针数 vis[x] = 1; ans2+= abs(z[x]); for(int i=head[x];i;i=e[i].next){ if(!vis[e[i].v])Dfs(e[i].v); } } int main(){ cin>>n>>m; for(int i=1;i<=n+2;++i){ for(int j=1;j<=m+2;++j){ a[i][j] = ++num; } } for(int i=1;i<=n;++i){//正面的所有边 cin>>s[i]+1; for(int j=1;j<=m;++j){//建边的时候正面的data也就是边权为0,便于判断 if(s[i][j] == '\\'){//建边 Add(a[i][j],a[i+1][j+1],0); Add(a[i+1][j+1],a[i][j],0); b[a[i][j]] = b[a[i+1][j+1]] = 1;//标记这里有线 } if(s[i][j] == '/'){ Add(a[i][j+1],a[i+1][j],0); Add(a[i+1][j],a[i][j+1],0); b[a[i][j+1]]=b[a[i+1][j]]=1;//同上 } if(s[i][j]=='X'){//X则对角建边 Add(a[i][j+1],a[i+1][j],0); Add(a[i][j],a[i+1][j+1],0); Add(a[i+1][j],a[i][j+1],0); Add(a[i+1][j+1],a[i][j],0); b[a[i][j]]=b[a[i+1][j]]=b[a[i+1][j+1]]=b[a[i][j+1]]=1; } } } for(int i=1;i<=n;++i){//反面的建边,以下的细节同上 cin>>s[i]+1; for(int j=1;j<=m;++j){ if(s[i][j] == '\\'){ Add(a[i][j],a[i+1][j+1],1); Add(a[i+1][j+1],a[i][j],1); b[a[i][j]] = b[a[i+1][j+1]] = 1; } if(s[i][j] == '/'){ Add(a[i][j+1],a[i+1][j],1); Add(a[i+1][j],a[i][j+1],1); b[a[i][j+1]]=b[a[i+1][j]]=1; } if(s[i][j]=='X'){ Add(a[i][j+1],a[i+1][j],1); Add(a[i][j],a[i+1][j+1],1); Add(a[i+1][j],a[i][j+1],1); Add(a[i+1][j+1],a[i][j],1); b[a[i][j]]=b[a[i+1][j]]=b[a[i+1][j+1]]=b[a[i][j+1]]=1; } } } for(int i=1;i<=num;++i){ if(b[i] && !vis[i]){//当前点没有访问过且有线 ans2=0; Dfs(i);//深搜求联通块的答案 if(!ans2)ans1+=2;//联通块答案为0,也就是环,因为一会要除以2,所以直接加上2 else ans1 += ans2; } } cout<<ans1/2<<"\n"; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号