7.6集训模拟赛9(老姚出出出出出题怪辟的的一天)

我差点就行信了,咳咳咳咳
A.精灵魔法(逆序对)
题目描述

输入格式

输出格式

样例
样例输入
3 1 2 3 2 1 3
样例输出
1
数据范围与提示

分析
这到题是归并排序(疫情在家水了这节,不会......)直接用暴力写的50分qwq。关于归并排序在代码里写详细一点。
Code
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e5+10; ll n; ll a[N],b[N]; ll ans; struct node{ ll x;//坐标 ll v;//速度 }e[N]; bool cmp(node a,node b){//按坐标排序 return a.x<b.x; } void merge(ll l,ll mid,ll r){ ll i=l;//指向前一个区间的首位 ll j=mid+1;//后一个区间的首位 ll k=0;//b数组 while(i<=mid&&j<=r){//两个区间都不为空 if(a[i]<=a[j]){//前一个区间的小于后一个区间的 b[++k]=a[i++]; } else {//不然 ans+=mid-i+1;//否则就会有mid-i+1个与a[j]组成逆序对 b[++k]=a[j++]; } } while(i<=mid){//前一个区间不为空 b[++k]=a[i++]; } while(j<=r){//后一个不为空 b[++k] = a[j++]; } for(ll i = l,k=1;i<=r;i++,k++){//拷贝到a数组 a[i]=b[k]; } } void mergesort(ll l,ll r){ if(l<r){//把区间分成两部分 ll mid=l+(r-l)/2; mergesort(l,mid);//递归左区间 mergesort(mid+1,r);//递归右区间 merge(l,mid,r);//归并排序 } } int main(){ scanf("%lld",&n); for(ll i = 1;i <= n;i++){ scanf("%lld",&e[i].x); } for(ll i = 1;i <= n;i++){ scanf("%lld",&e[i].v); } sort(e+1,e+1+n,cmp); for(ll i=1;i<=n;i++){ a[i] = e[i].v; } mergesort(1,n); printf("%lld\n",ans); return 0; }//over
B. 最小环
题目描述

输入格式

输出格式

样例
样例输入
2 3 3 1 2 1 2 3 1 3 1 1 4 5 1 2 2 2 3 2 3 4 2 1 4 2 1 3 5
样例输出
3 8
分析
正解:就是把与1的相邻的(临接边一个一个枚举)断掉后跑最短路,在加上段的这条边,取min值
奇葩的是堆优化的dijkstra在题库会卡掉4个点,用spfa就AC,看来这次“关于spfa,他没死”。
Code
#include<bits/stdc++.h> using namespace std; const int N = 4e5; const int INF = 0x3f3f3f3f; int t; int n,m; int x,y,w; int cnt; int head[N]; bool vis[N]; int dis[N]; //priority_queue<pair<int, int> > q; struct edge{ int to; int ne; int w; }e[N]; void add(int u,int v,int w){ e[cnt].to = v; e[cnt].w = w; e[cnt].ne = head[u]; head[u] = cnt++; } void spfa(int s){//标准spfa memset(vis,0,sizeof(vis)); memset(dis,0x3f,sizeof(dis)); queue<int>q; q.push(s); dis[s] = 0; vis[s] = 1; while(!q.empty()){ int f = q.front(); q.pop(); vis[f] = 0; for(int i = head[f];~i;i = e[i].ne){//由于head数组是初始化的-1所以i要去反 int v = e[i].to; if(dis[v] > dis[f] + e[i].w){ dis[v] = dis[f] + e[i].w; if(!vis[v]){ q.push(v); vis[v] = 1; } } } } } int main(){ scanf("%d",&t); while(t--){ cnt=0; memset(head,-1,sizeof(head)); scanf("%d%d",&n,&m); for(int i = 1;i <= m;i++){ scanf("%d%d%d",&x,&y,&w); add(x,y,w);//建双向边 add(y,x,w); } int ans = INF; for(int i = head[1];~i;i = e[i].ne){ int temp = e[i].w;//暂存这条边权 e[i].w = e[i^1].w = INF;//断边 spfa(1); ans = min(ans , dis[e[i].to]+temp); e[i].w = e[i^1].w = temp;//接回去 } if(ans == 0x3f3f3f3f)printf("-1\n");//...... else printf("%d\n",ans); } return 0; }
来份dalao的dij的
他就是没有断边,在遍历时特判了一下
#include<bits/stdc++.h> using namespace std; const int maxn = 1e4 + 5; const int maxm = 8e4 + 5; int n, m, cnt, head[maxn], vis[maxn], dis[maxn]; struct Edge{ int to, next, dis; }edge[maxm]; struct Node{ int pos, dis; Node(int x, int y){ pos = x; dis = y; } bool operator < (const Node &a)const{ return dis > a.dis; } }; void Add(int u, int v, int w){ edge[++cnt].to = v; edge[cnt].next = head[u]; edge[cnt].dis = w; head[u] = cnt; } void Dij(int s){ priority_queue<Node> q; memset(vis, 0, sizeof(vis)); memset(dis, 0x3f, sizeof(dis)); dis[s] = 0; q.push(Node(s, 0)); while (q.size()){ int cur = q.top().pos; if (cur == 1) return; q.pop(); if (vis[cur]) continue; vis[cur] = 1; for (int i = head[cur]; i; i = edge[i].next){ int v = edge[i].to; if (cur == s && v == 1) continue;//如果遍历到了初始边并且指向1号节点 if (dis[v] > dis[cur] + edge[i].dis){ dis[v] = dis[cur] + edge[i].dis; q.push(Node(v, dis[v])); } } } } void Init(){ cnt = 0; memset(head, 0, sizeof(head)); } int main(){ int T; scanf("%d", &T); while (T--){ int ans = 0x3f3f3f3f; Init(); scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++){ int u, v, w; scanf("%d%d%d", &u, &v, &w); Add(u, v, w); Add(v, u, w); } for (int i = head[1]; i; i = edge[i].next){ int v = edge[i].to; Dij(v); ans = min(ans, dis[1] + edge[i].dis); } if (ans >= 0x3f3f3f3f) cout << "-1\n"; else cout << ans << endl; } }
C. LGTB 与序列(恶心的数论?不,是数论dp,额dp)
题目描述
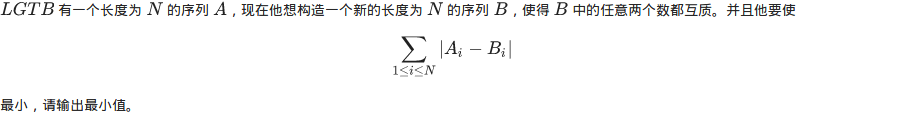
输入格式

输出格式

样例
样例输入
5
1 6 4 2 8
样例输出
3
数据范围与提示
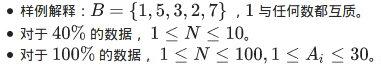
分析
因为A是≤30的,所以只用考虑58个数,因为如果大于了58,还不如取1(自己想一想),我们就选58之内的质数(只有16个),16??!!嗯,16!,啊,16??
16咋了,我还17呢!切!!!????扯啥呢,16状压啊。你扯啥呢,这道题状压,别瞎忽悠了。不是我想揍你,看下面!!!!!
Code
#include<bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; const int N=1<<20+1; int prime[] = {0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};//16个质数 int f[18][N];//表示处理到第i位,j状态时的最优解 int n,a[105]; int state[N];//存每个数的质因子的情况 bool cmp(int a,int b){//从小到大排序,尽量不给大的数配1 return a>b; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } sort(a+1,a+1+n,cmp); for(int i=1;i<=58;i++){ for(int j=1;j<=16;j++){ if(i<prime[j])break; else if(i%prime[j]==0){ state[i]|=(1<<(j-1)); } } } int maxn=1<<16; int ans=INF; memset(f,0x3f,sizeof(f)); f[0][0]=0; for(int i=1;i<=min(16,n);i++){ for(int S=0;S<maxn;S++){ for(int k=1;k<=58;k++){ if(!(S&state[k])){//判断之前是否选过了质因子,即判断是否合法 f[i][S|state[k]]=min(f[i][S|state[k]],f[i-1][S]+abs(k-a[i])); } } } } for(int S=0;S<maxn;S++){ ans=min(ans,f[min(16,n)][S]); } if(n>16){ for(int i=17;i<=n;i++) ans+=abs(a[i]-1); } printf("%d\n",ans); }
D. 步步为零(我也是没想到这是dp,还一直想搜索呢)
题目描述


输入格式

输出格式

样例
样例输入
4 2 3 1 -3 5 7 6 10 -2 20 -7 -5 -8 10 8 7
样例输出
0
数据范围与提示

分析
啊,这就是个dp,我们用一个bool型数组来记录,dp[i][j][k]前i行前j列能否组成k,详细的注解已经写道了代码里。downdowndown
Code
#include<bits/stdc++.h>
using namespace std;
const int N = 35;
bool dp[N<<1][N][6010];
int a[N<<1][N];
int tot,maxn;
int n;
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i++){
maxn=0;
for(int j = 1;j <= i;j++){//上半部分
scanf("%d",&a[i][j]);
a[i][j] = abs(a[i][j]);//全部换成绝对值,后面好处理
maxn = max(maxn , a[i][j]);
}
tot += maxn;//累加记录每一行的最大值
}
for(int i = 1;i < n;i++){//下半部分
maxn=0;
for(int j = 1;j <= n-i;j++){
scanf("%d",&a[n+i][j]);
a[n+i][j] = abs(a[n+i][j]);
maxn = max(maxn , a[n+i][j]);
}
tot += maxn;
}
int now = 0;
dp[2*n-1][1][tot] = 1;全图向上移了tot
for(int i = 2*n-1;i > n;i--){
for(int j = 1;j <= 2*n-i;j++){
for(int k = 0;k <= 2*tot;k++){
if(dp[i][j][k]){
now = k+a[i][j];
dp[i-1][j][now] = dp[i-1][j+1][now] = 1;//可以凑出now这种状态
now = k-a[i][j];//
dp[i-1][j][now] = dp[i-1][j+1][now] = 1;
}
}
}
}
for(int i = n;i>=1;i--){
for(int j = 1;j<=i;j++){
for(int k = 0;k <= 2*tot;k++){
if(dp[i][j][k]){//同上
now = k+a[i][j];
dp[i-1][j][now] = dp[i-1][j-1][now] = 1;
now = k-a[i][j];//
dp[i-1][j][now] = dp[i-1][j-1][now] = 1;
}
}
}
}
int ans = 0x3f3f3f3f;
for(int i = 0;i <= 2*tot;i++){
if(dp[0][0][i]){
ans = min(ans,abs(i-tot));
}
if(dp[0][1][i]){
ans = min(ans,abs(i-tot));//求最大值,(0,0)是因为表示的是在第0行没有选的时候可以凑出来的数,也就是所有状态加上了(1,1)的值之后的状态
}
}
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号