神秘姿势:把 K(2n) 分解成 2n-1 组完美匹配
这个姿势实在yhx的做题记录里看到的!大家可以去膜拜原题解
符号说明
\(K(n)\):\(n\) 个点的完全图
完美匹配:对于 \(2n\) 个点,一个大小为 \(n\) 的匹配就是完美匹配,也就是每个点都有恰好一个点跟它匹配。
姿势
这里的分解指的是对边集的分解。也就是说,\(K(2n)\) 一共有 \(\dfrac{2n(2n-1)}{2}=n(2n-1)\) 条边,一个匹配有 \(n\) 条边,咱把它分成 \(2n-1\) 个部分,满足每个部分都是一组完美匹配的边。
举例:\(4\) 个点,我们把它这样分解
\[\begin{cases}
(1,2),(3,4)\\
(1,3),(2,4)\\
(1,4),(2,3)\\
\end{cases}
\]
就是其中一种分解方法。
具体的,如何做呢?首先我们任选一个点,把它摆在中间,剩下 \(2n-1\) 个点围成一圈排起来。
不妨设中心点为 \(O=a_{1}\),剩下的点是 \(a_2,a_2...a_{2n}\)。
每次选一个 \(i\in[2,2n]\),连边 \(O\to a_i\),剩下的 \(2n-2\) 个点以 \(i\) 为对称轴,两两匹配。注意这个“对称”是在环上对称。而且注意,是剩下的 \(2n-2\) 个点,实现的时候务必判掉 \(1\) 和 \(i\) 两个点,要绕过去。
yhx的博客上有一张gif如下
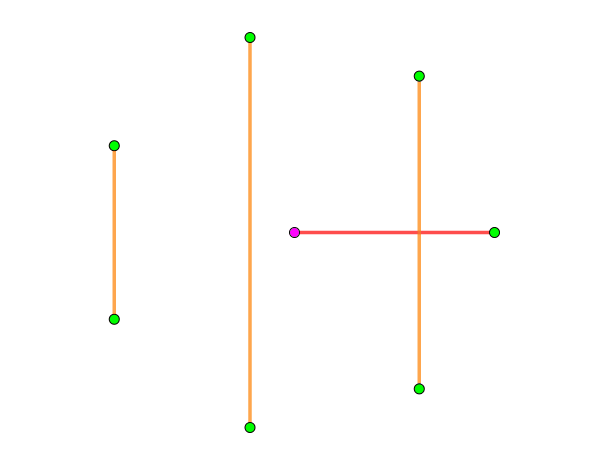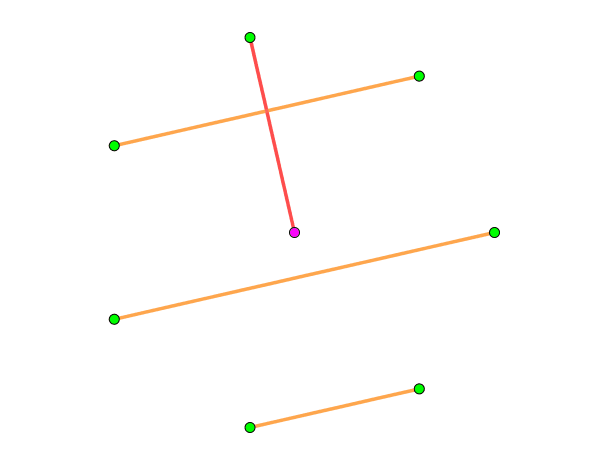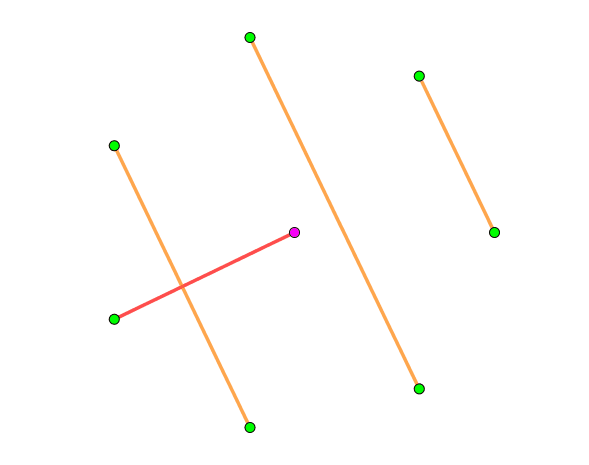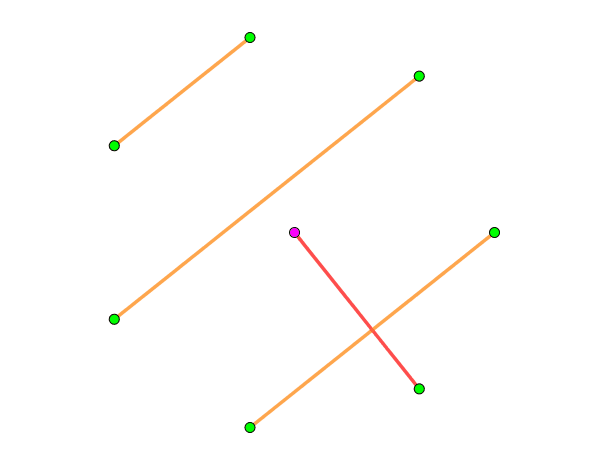


 浙公网安备 33010602011771号
浙公网安备 33010602011771号