数数专题
注：尚未完成，先发出来，然后去睡觉
数数，是一个从出生就开始学并一直学不会的东西
这里讲“数数”，是指：形如“计算满足xxx条件的方案数”的问题。
实现较复杂的问题会给代码。剩下的可以在 vjudge/原网站 上翻我的提交记录得到代码
注：我一般喜欢交vjudge，并且我的常用号是 LightningUZ_CF 而不是 LightningUZ
有一些数数，比如 GF 相关，会另外讲。
这里讲的主要是不用GF，用组合数，dp等技巧的数数题。
借助dp
动态规划是数数的好朋友，很多时候我们可以用动态规划解决数数问题。
有人称其为 “计数dp”。比如我们熟悉的背包，就是一种dp。
当然，和背包相关的dp，与数数的关系不大，不细展开。
来点例题：
CF814E
参考了LCA的做法，他的题解在 这里
LCA的题解太神仙了，导致我这个菜鸡几乎看一行式子睡一次觉，就为了想 “这里为啥-1？” 这种事情，睡了4、5觉才做出来
所以这里会仔细讲（
这题是比较纯正的dp，只用到了非常少量的组合数学内容，全他妈在讨论
我们发现这条件还挺多：最短路唯一，最短路递增，度数有限制，并且为 \(2\) 或 \(3\)。
“最短路递增”，想象一下最后的最短路数组，相同的应该连续。那我们可以把连续的一段相同的划开，称为 “段”。
注意到，相邻两个段的最短路应该正好相差 \(1\)。并且后面一段的每个点都会有 恰好一条 到上一段的边。
（如果没有，那最短路就不对；如果有两条以上，那最短路就不唯一）
段内部允许有边。
看到分段，很容易想到dp。虽然粗略一想似乎不太会，但我们不用急，慢慢来。
别的不管，先设 \(f(i)\) 表示分到第 \(i\) 段的方案数，这个状态怎么也得有。
然后我们按套路，枚举上一段的点 \(j\)，然后 \(f(j)\times w(j+1,i)\) 转移过来。\(w\) 函数表示转移系数。
仔细一想，这个转移好像和段里面有多少个点有很大的关系。那我们得再记一维表示点数。
\(f(i,j)\) 表示到第 \(i\) 段，最后一段分了 \(j\) 个点，方案数。
\(f(i,j)=\sum\limits_{k} f(i-j,k)\times w(...)\)
我们注意到这样还不太能做，因为 \(2\) 度点和 \(3\) 度点处理起来不太一样，所以这个 \(w\) 似乎不太能写出来。
那就记一下上一层有多少个 \(2\) 度和 \(3\) 度的点，记为 \(c_2,c_3\)，然后考虑它们在自己那一层（即，上一层）内部，以及和当前的这一层，如何匹配起来。
上一层的点数可以直接得知，就是 \(c_2+c_3\)。这一层的点数需要再记一下。
再一想，上一层的每个点到上上层都恰好有一条边。那这么说，\(2\) 度点其实只有 \(1\) 个插头，然后 \(3\) 度点有 \(2\) 个插头。所以转移函数的本质是要考虑这些 插头的匹配。
于是我们设这个转移的函数为， \(g(n,c_2,c_3)\) 表示：
- 这一层有 \(n\) 个点，上一层有 \(c_2\) 个点有 \(1\) 个插头， \(c_3\) 个点有 \(2\) 个插头；
- 上一层的更前面已经满足了限制，并且上一层到上上层的边已经连好了；
- 我们要考虑，上一层内部的匹配，以及上一层与下一层的匹配；
的方案数。
容易写出转移：\(f(i,j)=\sum\limits_{k} f(i-j,k)\times g(j,c_2,c_3)\) （\(c_2,c_3\) 很容易统计出来）
最后的答案就是 \(\sum\limits_{j} f(n,j)\times g(0,c_2,c_3)\)。
那我们把 \(g\) 搞出来就做完了。但是这个 \(g\) 看起来比较复杂，分情况讨论
以下称 “\(A\)” 表示只有一个插头的点，\(B\) 表示有 \(2\) 个插头的点
-
\(n=0\)
此时下一层没有点，那就只需要考虑层内的匹配
-
\(c_2=0\)，\(c_3>0\)
此时只有 \(B\) 点，那这样匹配一波，一定会形成若干个环。
我们枚举其中一个环来转移。
为了避免算重复，我们强制让枚举的那个环包含 \(B\) 点中标号最小的那个。
由于不能有重边和自环，环长至少为 \(3\)
得到转移： \(g(0,0,c_3)=\sum\limits_{i=3}^{c_3} N(i)\times \binom{c_3-1}{i-1}\times g(0,0,c_3-i)\)
其中 \(N(i)\) 表示 项链数，也就是排一个环的方案数。
组合数里面的 \(-1\) 是因为我们已经选好一个，接下来只要选 \(i-1\) 个
-
\(c_2,c_3>0\)
此时 \(A,B\) 点都有。我们考虑连一条边，这条边可能连接着：
\(A+A\)，\(B+B\)，\(A+B\)
注意到我们不应该考虑 \(B+B\)，因为它要么会在 \(g(0,0,*)\) 的时候被算到，要么会在考虑完 \(A,B\) 插头间的边之后，其中一个 \(B\) 变成 \(A\)
所以我们只需要考虑，一个 \(A\) 点和哪种点匹配了
为了避免重复，还是要强制选 \(A\) 里面编号最小的那个。
如果我们再选一个 \(A\)，那就有 \(c_2-1\) 种选法，并且两个插头都接起来，没了。这一部分是 \((c_2-1)\times g(0,c_2-2,c_3)\)
如果我们选一个 \(B\)，那就有 \(c_3\) 种选法。而此时，\(A\) 点插头没了，而 \(B\) 点的插头数从 \(2\) 个变成 \(1\) 个，也就便乘了 \(A\) 类点。于是 \(A\) 类点的数量并没有变化，只有 \(B\) 类点的数量少了一个。那这一部分是
\(c_3\times g(0,c_2,c_3-1)\)
综上，\(g(0,c_2,c_3)=(c_2-1)\times g(0,c_2-2,c_3)+c_3\times g(0,c_2,c_3-1)\)
-
-
\(n>0\)
此时我们需要考虑下一层的匹配
下一层的每个点都要找一个匹配。为了避免重复，我们考虑下一层里面标号最小的那个点和谁匹配。
它可能和 \(A\) 类点匹配，有 \(c_2\) 种选法，此时 \(A\) 类点少一个，\(B\) 类不变。即 \(c_2\times g(n-1,c_2-1,c_3)\)
它可能和 \(B\) 类点匹配，有 \(c_3\) 种选法。此时有一个 \(B\) 类点变成 \(A\) 类点，所以是 \(B\) 少一个 \(A\) 多一个，即 \(c_3\times g(n-1,c_2+1,c_3-1)\)
综上，\(g(n,c_2,c_3)=c_2\times g(n-1,c_2-1,c_3)+c_3\times g(n-1,c_2+1,c_3-1)\)
注意边界 \(g(0,0,0)=1\)
然后就可以先预处理出 \(g\)，然后对着式子搞 \(f\)，然后对着式子搞答案。
总的复杂度是 \(O(n^3)\)，非常显然。
AGC24E
这题是一个“计树dp”，通常有一种套路：\(f(i,...)\) 表示 \(i\) 个点的树，...，的数量。
不过这题，要搞出这颗“树”要花一些功夫。
首先考虑一个问题，题目问的是本质不同的 序列组数量，而同一种序列组可能有不同的插入方案，如何去重？
我们发现，重复当且仅当我们插入的数有一堆连续的重复。比如aaabb要变成aaabbb。
此时我们强行插在最后一个位置，然后方案就是唯一的了。
由于我们要让字典序递增，再分析一下这种插入方式的性质，我们发现：每次插入进去的元素，要比“顶掉”的元素的字典序 严格 大。
为了避免边界情况，我们令序列的最后有一个 \(0\)，并且我们不能插在 \(0\) 后面。那插入在最后的情况相当于是顶掉了 \(0\)，没问题。
我们考虑每个数的 “流向”。即，我们画一根线。当它被插进来的时候，就新建一个线头。如果它没有被顶掉，那这根线竖直向下，否则就斜着向右下。
比如说，序列组：
0
1 0
1 1 0
1 1 1 0
1 1 4 1 0
1 1 4 5 1 0
1 1 4 5 1 4 0
它的 “流向” 示意图如下：
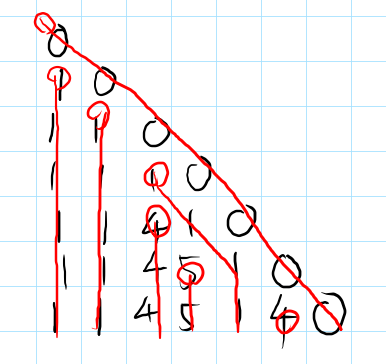
每个红色的圈圈表示一个线头的开始。用眼睛瞪这个图，结合脑子想，发现：
- 0一定是一条斜线向下
- 每一个 “线头” 一定比它上面的那个位置 严格 大（因为它要顶掉上面那个位置）
然后再一想，发现：我们可以把每个（0以外的）线头和它上面那个位置所在的线头连一条边。这样一定是颗树（因为“严格大于”这个东西不可能有环，并且显然连通）。我们考虑以 \(0\) 为根。
这颗树会有很多个叉，但是它的点权值在树上外向递增（即，父亲小于儿子）
考虑每个“线头”被插入进来的时间，我们发现这玩意很显然也递增。
那我们给树上的每个点两个权值，一个表示插入时间，一个表示填的数字。我们发现，如果知道了每个点的插入时间，也知道它的父亲，那我们其实就能唯一确定它去顶掉哪个点，再结合填的数字...我们就能唯一确定一个方案！（即，一个序列组）
于是变成了数树问题。
考虑到俩权值要递增，我们设 \(f(n,x)\) 表示，\(n\) 个点的树，根节点权值是 \(x\)，方案数。答案是 \(f(n+1,0)\)。
考虑根的所有子树，发现每个子树的根的权值都 \(\ge x+1\)，并且一共有 \(n-1\) 个点。这是一个森林计数。
而我们发现“森林计数”和“树计数”可以互相转移！不妨换一下状态，设：
-
\(f(n,x)\) 表示 \(n\) 个点的森林，每个树的根的权值都 \(\ge x\)，方案数
-
\(g(n,x)\) 表示 \(n\) 个点的树，根的权值是 \(x\)，方案数。
首先，\(g(n,x)=f(n-1,x+1...k)\)。我们用后缀和优化掉这个东西。
然后 \(f(n,x)=\sum\limits_{i=1}^{n} f(i,x)\times g(n-i,x)\times \binom{n}{i}\)。
这个很明显，我们选出前面 \(i\) 个是森林，然后剩下的 \(n-i\) 个单独构成一颗树，就行了。
\(\binom{n}{i}\) 是因为我们要给它分配一个 “插入时间”。前面的 \(f,g\) 这样合并不会算重是因为，虽然它会算重树结构，但是此时的插入时间那一维不会重。
注意到这样的 \(f\) 是至少两棵树的。我们给它加上 \(g(n,x)\) ，就把独木成林的情况考虑到了。
然后就这样转移一波即可，答案是 \(g(n+1,0)\)
AGC16F
好家伙，刚数完树，开始数DAG了
先拿SG函数做一波转化，再考虑反面，相当于要数 \(SG(1)=SG(2)\) 的方案数。
然后我们考虑按 \(SG\) 的值把图分层。
考虑把 \(S\) 中 \(SG=0\) 的那些点抽出来，发现：其余每个点到它们至少一条边，并且这些点内部不能有边。
抽出来之后，把它们删掉，发现剩下的点里面，整体 \(SG\) 都 \(-1\)，满足同样的性质，即，最优子结构。
于是考虑dp。设 \(f(S)\) 表示 \(S\) 中最小的两个元素 \(SG\) 值相同的情况，\(U\) 表示全集，认为是 \(1...n\) 组成的集合。然后答案就是 \(2^m-f(U)\)
注意到 \(S\) 不能把 \(1,2\) 分开，否则这个dp状态就不可用。然后枚举 \(S\) 的子集 \(T\)，记 \(S/T\) 表示 \(S\cap (\overline{T})\)，即 \(S\) 去掉 \(T\) 的那一部分。
那么 \(S/T\) 中每个点到 \(T\) 至少一条边 （和上题挺像，少了度数限制），\(T\) 到 \(S/T\) 的边可以瞎连，不影响。
\(T\) 内部的边 全部不能连 ，而 \(S/T\) 内部的连边通过 \(f\) 得到。
那就是 \(f(S)=\sum\limits_{T\subsetneqq S} f(S/T)\times w_1(T,S/T)\times w_2(S/T,T)\)
设 \(E(u,S)\) 表示 \(u\) 有多少出边到 \(S\)。可得转移函数：
\(w_1\) 表示瞎连方案数，\(w_1(S_1,S_2)=\prod\limits_{x\in S_1} 2^{E(x,S_2)}\)
\(w_2\) 表示连至少一条边的方案数，把 \(w_1\) 的转移变成 \(\prod (2^{...}-1)\) 就行了，很明显 \(-1\) 就可以去掉不连的方案。
这两个都可以每次预处理出 \(E\) 之后，扫一遍算出来。
于是总复杂度是 \(O(n\times 3^n)\)。
小结
我们可以先研究一波问题的性质，把问题转化成好做的形式，或者是提炼出我们真正需要知道的东西，再用dp做。
（接下来就开始飞了）
dp+复杂度平衡: loj547
首先考虑一个naive dp:
设 \(f(i)\) 表示长度为 \(i\) ，满足条件的01串个数。那么： \(f(i)=2f(i-1)-f(i-m-1)\)。
这玩意有两种搞法：
- 注意到 65537 是个 NTT 模数，对于 \(m\le 8192\) 的数据（我实现的不太精细，如果精细实现可以做到 \(m\le 32768\)），可以跑一个常系数齐次线性递推，\(O(m\log m\log n)\)
- 当 \(m>8192\) 的时候，注意到 \(\dfrac{n}{m}\) 非常小。我们给这个递推赋予组合意义：\(u\) 到 \(u+1\) 有 \(2\) 条重边，\(u\) 到 \(u+m+1\) 有 \(-1\) 条重边，求方案数。我们枚举跳了多少条 \(+(m+1)\) 的边，计算出跳了多少条 \(+1\) 的边，然后用组合数瞎jr算一下方案数加起来就行；复杂度 \(O(\dfrac{n}{m})\)。
综合两种做法，就可以过了。
注意一个细节：做法1的递推里面，边界是：当 \(i<m\) 时，\(f(i)=2^i\)；\(f(m)=2^m-1\)。
而 \(f(m)=2^m-1\) 是我们手动设置的，如果按做法2直接跑，得到的是 \(f(m)=2^m\)。容易发现，只有这一位不对。
如何把它修正回来？（修正主义）
设做法2跑一个 \(n\) 得到的方案是 \(g(n)\)，也就是在DAG上从 \(0\) 跑到 \(n\) 的方案数。
一个很显然的想法是，我们直接跑这个计数，相当于是给 \(f(m)\) 加了 \(1\) 之后做上面的递推。不合法的部分，就是这个 \(f(m)\) 增加 \(1\) 之后的影响。考虑组合意义，这个影响就相当于在 DAG 上从 \(m\) 走到 \(n\) 的路径数。由于这个DAG的边只和点的相对位置有关，所以这个方案数就是 \(g(n-m)\)。
所以我们得到 \(f(n)=g(n)-g(n-m)\)。
注意到 \(g(n+1)=2g(n)-g(n-m)\)，所以这个式子也等于 \(g(n+1)-g(n)\)。
不过我没想明白它的组合意义。评论区大佬也可以讲一下，如何形象一点的理解 \(g(n+1)-g(n)=f(n)\) 这件事情。
dp+压缩自动机: CF506E
众所周知，一些dp可以用自动机的语言写出来，转化成自动机上的数路径问题
对于一个自动机，众所周知，我们可以压缩它
有以下几种策略：
- 转移边有很多重合部分，把它压起来，如SAM
- 有用的状态数很少，如PAM （本质不同回文串 O(n) 个）
- 根据问题特点，改写自动机，并按照上面两个方法压缩，如，本题
先写一个 naive-dp。设 \(m=|s|\)，\(N\) 表示串的总长，即 \(n+m\)。
\(f(i,l,r)\) 表示长度为 \(i\) 的回文串，使得 \(s[l:r]\) 是它子序列的方案数。
每次考虑在串的两边加字符，并考虑它是 \(s_l,s_r\)，还是其它。然后讨论一波：
边界：
- 如果 \(i=0\)，\(f(i,l,r)=[l>r]\)
- 如果 \(i=1\)，\(f(i,l,r)=[l\ge r]\)
- 如果 \(l>r\)，\(f(i,l,r)=26^{\lceil \frac{i}{2}\rceil}\)
转移：
- 如果 \(s_l=s_r\)，\(f(i,l,r)=25f(i-2,l,r)+f(i-2,l+1,r-1)\)
- 如果 \(s_l\neq s_r\)，\(f(i,l,r)=24f(i-2,l,r)+f(i-2,l+1,r)+f(i-2,l,r-1)\)
然后 \(f(N,1,m)\) 就是答案了。
把状态 \((i,l,r)\) 里面的那个 \(i\) 看成是在走步（每次走两步，分奇偶讨论下就行），并把 \((l,r)\) 建点。
如果 \(l>r\)，我们称其为“结束点”，记作 \(E\) 类；如果 \(s_l=s_r\)，称其为“相同点”，记作 \(A\) 类；否则称为 “不同点”，记作 \(B\) 类。
我们把点排成方阵。\(A,B\) 构成一个上三角，\(E\) 都在左下角。
对角线上一定都是 \(A\)。
一个 \(A\) 点，它可以向左下角连一条边；一个 \(B\) 点，它可以向正左/正右连一条边。
每个点上都有自环。根据dp方程，\(A\) 点有 \(25\) 条自环，\(B\) 点有 \(24\) 条自环，\(E\) 点有 \(26\) 条自环。
我们从 \((1,m)\) 开始走，走到 \(E\) 点结束，可以走边，可以走自环，走 \(N\) 步，问方案数。
暴力矩乘，\(O(m^6\log n)\)，过不去。
我们考虑压缩这些点构成的自动机。注意到我们的 \(E\) 点只需要两条对角线，\(j=i-1\)，\(j=i-2\)，因为我们一定会走到这两条线之一就停止。
根据这个，我们走一条路下来，\(r-l+1\) (长度) 肯定会从 \(m\) 变化到 \(0/-1\)。注意到，走一个 \(A\) 长度 \(-2\)，走一个 \(B\) 长度 \(-1\)。设我们走了 \(a\) 个 \(A\)，\(b\) 个 \(B\)，那么 \(a=(m-b+1)/2\)
也就是说，确定了 \(b\) 就可以确定 \(a\)。
然后我们注意到，一条路径的贡献，只和 \(a,b\) 有关，贡献是 \(25^a\times 24^b\times 26/1\)，和经过的顺序并没有关系。
\(a,b\) 值相同的路径可能有很多条，但是我们现在知道，本质不同只要O(m)条
设 \(P(b)\) 表示经过了 \(b\) 个 \(B\) 的路径条数。然后我们的自动机就只需要关心 \(A,B\) 的数量了。
注意到我们怎么也得经过一个 \(A\)，那么 \(b\) 的值域是 \([0,m-1]\)，\(a\) 的值域是 \([1,(m+1)/2]\)
我们建出这样的一个自动机：点 \(B_i\) 表示经过 \(i\) 个 \(B\) 对应的状态，\(A_i\) 同理。
为了让它俩能 “拼起来”，我们考虑把它俩对接，如下：
\(B_{m-1}\to B_{m-2}\to ... \to B_{1}\to A_{1}\to A_{2}\to ... \to A_{(m+1)/2}\)
每个 \(A_i\) 的下面再挂一个 \(E_i\) 表示结束。
每个 \(B\) 点有 \(24\) 个自环，\(A\) 点有 \(25\) 个自环，\(E\) 点有 \(26\) 个自环。
这样，枚举 \(b\)，计算出 \(a=(m-b+1)/2\)，\(B_b\) 到 \(E_a\) 的路径就和原图上的 本质不同路径 一一对应了。
走一步相当于长度 \(+2\)。
如果 \(N\) 是偶数，把这个图的邻接矩阵搞出来求个 \(N/2\) 次幂，统计一下答案就行了。
如果 \(N\) 是奇数，稍微复杂些。
我们令最后一步的长度只 \(+1\)。那我们会走 \((N+1)/2\) 步。
不合法，当且仅当从一个 \((x,x+1)\) 的 \(A\) 类点转移到 \(E\)。因为它要做最后一步，但它需要加两个相同字符，而我们强制让最后一步只加一个字符，就不能真正的匹配上。
我们把这种情况减掉即可。手动推一推，发现这种情况下有 \(2a+b=m\)。而且我们只能恰好走上 \(E\) 点，而不能在上面绕自环。
这就等价于我们走 \((N+1)/2-1=(N-1)/2\) 步，走到一个 \(A\) 类点。
所以我们就把那个矩阵的 \((N-1)/2\) 次幂算出来，枚举 \(a\)，计算得 \(b=m-2a\)，求 \(B_b\) 到 \(A_a\) 的路径数量的和，就是不合法的方案数。
不要忘记乘个 \(P\)。
容斥原理
每个的容斥背后，都有一个默默支持它的反演
常见的容斥，容斥系数是正负/正负+组合数的，本质是二项式反演
容斥系数带 \(\mu\) 的，本质是莫比乌斯反演，本质的本质是在质因数的集合上二项式反演，\(\mu\) 是其容斥系数。
二项式反演，可以搞出来一堆集合的交/并，或者把“恰好”转换成“至少”
如，CTS2019 随机立方体
容斥也可以结合dp，通过dp记录容斥的贡献来做
如，CTS2019 氪金手游
由于这两题都属于概率期望，所以这里不讲（雾）
其实概率期望的本质也是数数
只不过我懒得再写一遍了qaq
去翻 “概率期望” 那篇罢
注，莫比乌斯容斥和这个东西的关系不大，所以这里略
naive题：51nod 1829
考虑直接瞎jr射，方案数是 \(n^n\) ，但肯定会有不射满的 （戴黄看黄）
然后我们考虑容斥，容易想象到，我们应该这样做：
射在 \(n\) 个数内 - 射在 \(n-1\) 个数内 + 射在 \(n-2\) 个数内...
这样的容斥显然是对的。想象一下正负号，得到：答案为
可以用这个题来热热身。
如果您对容斥比较熟悉，不用动笔，用嘴巴就可以搞出这个题了。
反之，如果您用嘴巴切了这个题，说明您的容斥很强！
ZJOI2016 小星星
同样涉及到一个映射的问题，考虑和上个题类似的做法：我们先不保证射满，然后容斥。
先枚举一个集合 \(S\)，并限制我们必须射在这里面。然后做树形dp：\(f(u,x)\) 表示，\(u\) 射到 \(x\)，\(u\) 子树射的方案数。
枚举 \(v\) 射到了 \(x'\)，那在原图上 \(x\) 和 \(x'\) 之间就要有边。如果有，就把这个方案加到 \(f(u,x)\) 里面。
最后 \(f(1,*)\) 的和就是 \(S\) 的答案，容斥一下加起来即可。
noiac2201 连续子序列: dp出容斥的贡献
（noi.ac的题有权限，这里给出题意）
称一个排列的子串为顺子，当且仅当：这个子串里两两之间差的绝对值为 \(\pm 1\) （即，连续单增/单减）
求 \(n\) 个数的排列中，有多少种排列满足它所有顺子的长度都 \(\le m\)。模 \(1e9+7\)。
\(m\le n\le 5000\)。
考虑反面，我们枚举它有多少个长度为 \(m+1\) 的顺子（枚举左端点），其余位置任意选，设这个方案为 \(c(i)\)。那么答案为
\(c(0)-c(1)+c(2)-c(3)...=\sum\limits_{i}(-1)^i c(i)\)
然后我们发现，两个顺子如果有交，那它们必须同时递增/递减，然后我们就可以把它合并成一个大块的顺子，称为一 “块”
对于一个块，它里面选多少个长度为 \(m+1\) 的顺子，我们其实并不知道。但是我们只关心它们的方案数乘上容斥系数的和（因为这玩意就是答案）
对于块之外的东西，每个位置都是独立的数，称为 “单点”
假设我们有 \(a\) 个块，\(b\) 个单点，可以先安排出它们的相对顺序，\((a+b)!\) 种方案，然后就可以唯一确定它们里面填什么数了。
对于一个块，它可以增或者减，那就还有 \(2^a\) 种分配方法。
所以它们仅填数字的方案（即，不考虑结构和容斥系数）就是 \(2^a (a+b)!\) 种。
设 \(f(i,a,b)\) 表示前面 \(i\) 个数，选了 \(a\) 个块，\(b\) 个单点，容斥贡献和。
如果第 \(i\) 个位置是单点，那么 \(f(i-1,a,b-1)\) 贡献到 \(f(i,a,b)\)
如果第 \(i\) 个位置属于一个块，那就枚举一个 \(j\) 表示上一块的结尾，\(f(j,...)\) 贡献过来。
发现这样并不对，因为我们不能直接用 \(f\) 贡献，因为 \(f\) 可能会有单点出来。
那我们再搞一个 \(g(i,a,b)\) ，表示强制令 \(i\) 为一个块的结尾，的方案数。
那 \(f(i,a,b)=g(i,a,b)+f(i-1,a,b-1)\)
考虑 \(g\) 的转移：
- 如果当前选的顺子不和以前的重叠，贡献和是 \(g(i-m-1,a-1,b)\)。由于多选了一个，容斥贡献就乘一个 \(-1\)。
- 反之，就和以往的某个顺子重叠了。那以前的顺子，它的右端点要在 \([i-m,i-1]\) 里面，并且选了这个顺子之后，容斥系数乘 \(-1\)，而块数不变，因为重叠了
可得：\(g(i,a,b)=-f(i-m-1,a-1,b)-g(i-m...i-1,a,b)\)。后面的 \(...\) 表示求和（这样写直观些）
然后我们可以用前缀和优化掉这个东西，复杂度 \(O(n^3)\)。
你开开心心的准备去写，一看数据五千。
然后你发现这个转移其实和 \(a+b\) 的关系比较大，注意到每次 \(a+b\) 这个东西只会变化一个 \(-1\) 或者不变。
但我们也不能只记一个 \(a+b\)，因为 \(a\) 还要贡献一个 \(2^a\)
那我们为什么不把这个 \(2^a\) 的贡献也搞进来呢？那就只需要记 \(a+b\) 了。
我们记 \(F(i,s)=\sum\limits_{a+b=s} 2^a\times f(i,a,b)\)，\(G(i,s)\) 同理。
我们把 \(F,G\) 的sigma里面的 \(f,g\) 用上面的转移化开，整理，把它们也搞成 \(F,G\) 的形式。得到：
\(F(i,s)=G(i,s)+F(i-1,s-1)\)
\(G(i,s)=-2F(i-m-1,s-1)-G(i-m...i-1,s)\)
为啥有一个 \(2\)？注意到那个 \(a-1\) 变成 \(a\) 的过程中，\(2^a\) 这个东西要变化的。
然后注意到空间开不下，考虑滚动数组。
接下来是一个 典 中 典： 如何滚 \(i\)？
注意到 \(i\) 这一维不太好滚。
所以我们滚 \(s\)。
这里 是完整的事件（
组合意义转化
很多东西具有一个组合意义
比如上面提到 \(f(i)=2f(i-1)-f(i-m-1)\) 的那个递推，它就可以看成DAG上的路径计数。
同时，\(n^m\) 这个东西，也具有很好的意义：\(n\) 个数，选 \(m\) 次，选一个数之后不删除，方案数就是 \(n^m\)。
管道取珠
对于第 \(i\) 种序列， \(a_i^2\) 相当于：取两次珠子，方案相同，且均为第 \(i\) 种序列的方案。
那么我们取两次珠子，方案相同，方案数就是 \(\sum a_i^2\)
接下来就好做了，注意到数据范围非常小，设 \(f(a,b,a',b')\) 表示：第一次取 \(A\) 的 \(a\) 个，\(B\) 的 \(b\) 个第二次取 \(A\) 的 \(a'\) 个，\(B\) 的 \(b'\) 个，相同，的方案数。
注意到 \(a+b=a'+b'\)，故省去 \(b'\)，然后滚一下就行了。
AGC13E
和上一题类似。一段长度的平方，就相当于在这一段里面选两个位置的方案数。
而把这些平方乘起来，就相当于是在前 \(i\) 个里面选 \(2k\) 个格子的方案数，根据乘法原理。
先不考虑障碍。设 \(f(i,0/1/2)\) 表示在前 \(i\) 个位置里面分段之后选，最后一段里面选了 \(0/1/2\) 个，的方案数。
第一种是，在 \(i-1,i\) 这里划开一段，然后 \(i\) 这个位置把当前的 \(j\) 个格子全部选掉。这种方案是 \(f(i-1,2)\)，前提是这一个位置不是障碍。
第二种是，\(i\) 和 \(i-1\) 在一段，考虑前面选了几个，然后 \(i\) 这个位置上选剩下的（可能为 \(0\)）。枚举一个 \(k\le j\)，这样的方案数是 \(\binom{j}{k}\times f(i-1,k)\)。
于是，\(f(i,j)=f(i-1,2)+\sum\limits_{k=0}^{j} f(i-1,k)\times \binom{j}{k}\)
对于没被障碍隔开的一段，用矩阵优化转移。障碍特判一下就行。
复杂度 \(O(m\times 2^3\times \log n)\)。
noiac 2448,2327
这两题的共同点是，需要求：长度为 \(n\) 的序列，每个数在 \([1,m]\) 间。设 \(L\) 表示最长连续相同段，求 \(L\) 的分布（即，对于每个 \(i\)，求 \(L=i\) 的方案数）
注意到，恰好不太好做，但是“不超过”感觉挺能做。
那我们现在要求最长连续相同段不超过 \(x\) 的方案，设为 \(g(i)\)。
考虑 \(i\) 所在的那一段多长，有转移：\(g(i)=(m-1)\times (i-m...i-1)\)。
注意一个细节：我们认为每一段都只能取 \(m-1\) 种，实际上第一段是可以取 \(m\) 种的。
最后乘一个 \(\dfrac{m}{m-1}\) 才是真正的答案。
前缀和优化，设 \(s\) 为 \(g\) 的前缀和。然后 \(s(i)-s(i-1)=(m-1)\times [s(i-1)-s(i-m-1)]\)。
移项，得 \(s(i)=m\times s(i-1)+(1-m)\times s(i-m-1)\)
然后和上面的一个转化类似：把它看成DAG上的路径计数。
枚举跳了多少次 \(m+1\)，复杂度 \(O(\dfrac{n}{m})\)。枚举 \(m\)，这样算，复杂度是调和的。
然后就得到了 \(s\)。取差分得到 \(g\)。然后发现 \(g\) 的差分就是 \(L\) 分布了。
复杂度 \(O(n\ln n)\)。
奇技淫巧
有这样一个式子，合法方案书=瞎选方案数*正确率。
假设我们能知道正确率，那问题就简单了。
noiac 2034
注意到 \((A,B)\) 的方案可以和 \(A,B\) 拼起来的方案一一对应。
现在问题变成一个序列：知道它有 \(a\) 个 \(1\) ，\(b\) 个 \(-m\)（和为 \(s=a-mb\)，保证是正的），每个位置的前缀和都是正的，求方案数。设 \(n=a+b\) 为序列长度。
考虑一个序列的所有循环同构，我们发现，它一共有 \(n\) 个循环同构，而其中的恰好 \(s\) 个满足前缀和都是正的。
假设这个结论对，那就太好做了，答案是 \(\binom{a+b}{a}\times \dfrac{s}{n}\)。这就是 “瞎选方案数”乘以“正确率”。
证明如下
对于一个序列，我们把它写无限遍。
设 \(las(x)\) 表示，前缀和最后一次为 \(x\) 的位置。由于序列和为正，每过一个周期和就会增，所以这个 \(las\) 的值是有限的。
对于 \(i\in [1,s]\)，考虑 \([las(i)+1,las(i)+n]\) 这一段区间。根据 \(las\) 的定义，\(las\) 后面所有前缀和都 \(>i\)。
那这么说，这一段区间的前缀和都严格的大于 \(i\)。 考虑区间内部的前缀和，设 \(p\in [las(i)+1,las(i)+n]\)，则内部前缀和就是 \((las(i),p]\) 的区间和，即 \(s_p-i\)。我们知道 \(s_p>i\)，所以这个和大于 \(0\)。
那我们把这一段区间取出来，它的每个位置前缀和都 \(>0\)，是这个序列的一个循环同构。
所以我们有至少 \(s\) 个循环同构，使得它们任意位置前缀和 \(>0\)
也容易发现，对于 \(i>s\)，它取出来的这段序列和 \(i-s\) 是本质相同的，所以不能算。
所以我们只有 恰好 \(s\) 个循环同构是满足条件的。
