CTS2019 部分题解
CTS2019 部分题解
Counting, Totaling, Summing。我们数数，我们统计，我们求和。
随机立方体
概率可以变成方案数/总方案数。
题面的 \(n,m,l\) 太丑，换成 \(a,b,c\)，为长方体的长宽高。
设 \(N=abc,n=\min(a,b,c)\)
首先观察到选 \(k\) 个极大的点，要保证剩下的恰好都不是极大点，非常困难。于是考虑容斥，或者叫二项式反演。
设 \(f(k)\) 表示至少有 \(k\) 个极大点方案数，\(g(k)\) 表示恰好 \(k\) 个极大点方案数。那么：
\(g(k)=\sum\limits_{i=k}^{n} f(i)\times \binom{i}{k}\times (-1)^{i-k}\)
那接下来如果能求出线性求出所有 \(f\)，就可以线性求出 \(g\)。
对于方案数，我们分几步走：
- 选出来这 \(k\) 个点
- 填数
对于数数/概率题，把方案分步做，再用乘法原理合并，是一种常见的考虑方法。
首先一个极大点在三个面里都是最大值，并且 \(nml\) 个值是两两不等的，那肯定不能有极大点的 \(x,y,z\) 坐标相同。所以选位置的方案就是 \(n^{\underline{k}}m^{\underline{k}}l^{\underline{k}}\)。注意到同一种方案包含的 \(k\) 个位置是 无序 的，所以除一个 \(k!\)。
接下来是填数字的方案。我们设 \(A_i\) 表示第 \(i\) 个极大点， \(D_i\) 表示 \(A_i\) 能够“管辖”的点集，也就是跟它 \(x\) 坐标或 \(y\) 坐标或 \(z\) 坐标相同的点的集合。设 \(D=D_1\cup D_2...D_k\)。
注意到 \(D\) 集合中的点是受限制的，要比控制它们的那些极大点小。而 \(D\) 集合外面可以瞎几把填。
考虑 \(D\) 的大小。似乎不太好考虑，考虑 \(\overline{D}\) 的大小。\(\overline{D}\) 相当于所有极大点都管不着的点集。那对于每一维，都不能与 \(k\) 个点的任意一个相同，而极大点的三维坐标都是两两不等的，所以直接 \(-k\) 就行。那就是 \((n-k)(m-k)(l-k)\)
那我们再减回来就行，\(|D|=nml-(n-k)(m-k)(l-k)\)
那现在来考虑“填数”这一步。
除了 \(D\) 外的 \(N-|D|\) 个数瞎几把选，方案数是 \((N-|D|)!\)。
对于这 \(|D|\) 个数，我们可以先选 \(|D|\) 个数，再看考虑如何排列。选的方案数是 \(\binom{N}{|D|}\)。
对于填的方案，我们手玩一下发现，一个位置可能要满足好几个限制，这是坠难受的。但是我们又仔细一想，它要满足的这些限制之间，还有一层套一层的关系。
如下图。由于三维不好画，画成二维，清楚一些。
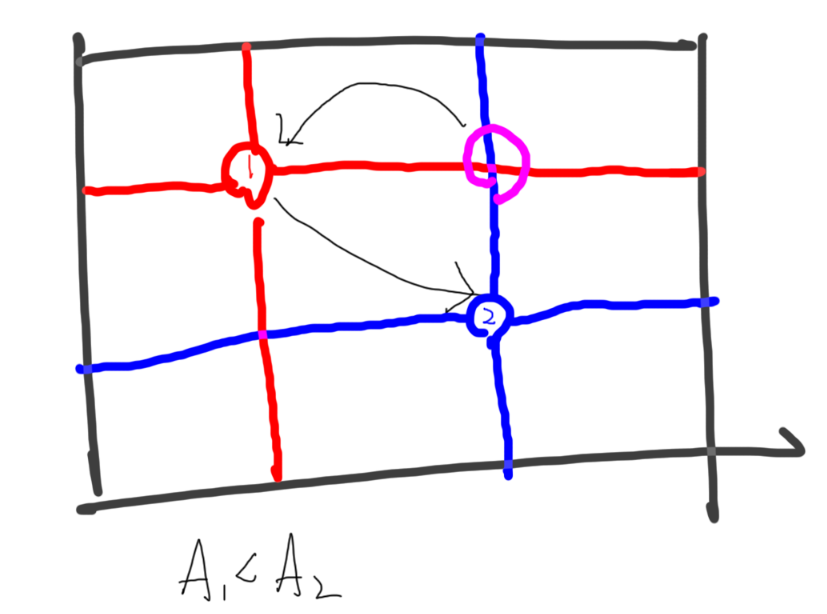
如图，如果红色比蓝色小，紫色同时受两者管辖，那么可以认为它是先比红色小，然后红色比蓝色小。根据不等式的传递性，这样转换一波很显然是等价的。
但是这样就很有意思了，我们把图画出来，发现它好像可以搞成一颗树。感性的想象一下，就是每个点找一个最近的比它大的连过去一条边，最大的不连边，肯定会连出来一棵树。翻译成理性一点的话说，
- 对于一个极大点：连到比它大的最小的那个极大点（后继），最大那个除外
- 对于一个非极大点，但在 \(D\) 集合中的点：连向管它的最小的那个极大点
这样一共有 \(|D|-1\) 条边，每走一条fa边，值一定变大，并且会停在最大的那个极大点上。于是这个图一定是颗树。
然后问题变成树的拓扑序问题，就是点数阶乘除以每个点size的积。那我们知道size就行了。
对于一个在 \(D\) 中不是极大点的点，那它的size肯定是 \(1\)，直接不管；否则当前点是极大点，那它的子树就是比它小的极大点的 \(D\) 集合的并。
注意到，\(k\) 个 \(D\) 集合的并大小肯定是 \(nml-(n-k)(m-k)(l-k)\)，无论这 \(k\) 个点在哪。
于是这颗树的拓扑序数为：
这就是填数字进来的方案数
我们总结一下式子，
注意到 \((N-|D|)!\times D!\times \dfrac{1}{N!}\)，与 \(\binom{N}{D}\) 恰好抵消。此时剩下：
这个东西就是 \(f(k)\) 了，显然可以预处理做到全线性算。
氪金手游
这题是一个随机套随机的模型，先随机一个 \(w\)，然后随机选点。
我们可以运用 这个结论，发现我们相当于要求概率的期望值。
先考虑对于确定的 \(w\)，满足条件的概率咋算。
注意到如果我们把有向边变成无向边，那这个图就是一棵树
如果有向边全是内向/外向，那倒是可以拓扑序做。很遗憾，不能，两种边是很可能同时存在的。
我们可以钦点，把所有边都想办法变成外向的。但有些边就是内向，那咋办呢？
做心理辅导 容斥。对于一条内向的边，把方案数看成是：（没有限制的方案数）-（外向的方案数）
暴力的容斥是 \(O(2^{n-1})\) 的，就是把这一堆乘起来的括号拆开。快，实在是快。
观察拆开的项，如果有奇数个外向，那系数是 \(-1\)，否则系数是 \(1\)。所以我们直接把容斥系数放进dp里，dp一遍即可。
接下来我们考虑带上期望一起算。对于当前的 \(u\)，它的子树里会有一些边是没有限制的。对于没有限制的边，我们把边切掉就行了。然后会裂开变成若干连通块，设 \(u\) 所在那个块里面的点 \(w\) 的和为 \(W\)。那我们这样随机抽一波，上来就抽到 \(u\) 的概率是 \(\frac{w_u}{W}\)。
考虑记 \(f(u,s)\) 表示 \(u\) 子树里切掉无限制边后，\(u\) 所在连通块的点 \(w\) 的和为 \(W\)，对答案的贡献（带容斥系数）和。
对于 \(u\) 的儿子 \(v\)，如果是一条外向边，非常的simple，直接把它俩卷积起来就行。
如果是一条内向的边，分成两个项，没限制-外向。
“没限制”这个项，就是 \(f(v,*)\rightarrow f(u,s)\) 即可。\(v\) 可以任意取，因为这条边断了，对 \(u\) 的连通块和没有影响。
“-外向”这个项，要取个负，上面的+=改成-=，就行了。其实就是所有的容斥系数都变化了 \(-1\) 倍。
像这样dp一遍，\(f(1,*)\) 就是答案了。
