sqrt数据结构 笔记
sqrt数据结构 笔记
毒瘤ds
一些约定
有一个一直出现的叫法,叫 “cnt数组”,是我喜欢这样叫,也不知道对不对。它是维护值域的,\(cnt(i)\) 表示有多少个值等于 \(i\)。
分块
啥是分块
观察这样一件事,我们现在要在序列上单点修改, 并维护区间和
如果我们直球的做,修改 \(O(1)\), 而询问是 \(O(n)\)
如果我们直球的维护前缀和, 修改 \(O(n)\),而询问是 \(O(1)\)
第一种方法我们相当于把每个数独立开来看,第二种方法我们相当于把所有数放在一块看(前缀和相当于干这个事情)。
有没有一种折中的方法,平衡两个复杂度? 先不说线段树,树状数组
我们可以考虑设置一个阈值 \(B\),每 \(B\) 个看成是一 块。
对于一次区间上的操作,覆盖到的完整的一块,成为“完整块”;不完整的,称为”散块“。如下图,红色是完整块,而绿色是散块(摘自lxl的分块ppt)

完整块的总数才 \(n/B\),其数量不会超过 \(n/B\);而散块的数量也显然小于 \(2B\)。
如果我们取 \(B=\sqrt{n}\),两块就平衡了,复杂度就都是 \(O(\sqrt{n})\) 的。当然,有些题目的数据不同,可能需要自己调整 \(B\) 的大小。
这样做的好处是,对于散块,我们可以一个一个搞,很方便处理;对于完整块,可以进行整体操作,也很方便,以此支持一些复杂的操作(很多操作甚至不能线段树,树套树,之类的)。
以上,便是对分块的一个初步认识
它有一些有意思的别名,后文中说 “sqrt technology”,或者是 “块速”,都是指这个
为啥要分块
众所周知,有线段树这样一种东西。
众所周知,有树套树这样一种东西。
但是它们能够解决的问题十分有限,并且空间较大(树套树/可持久化线段树)。如果区间的操作/询问并不能支持快速的区间合并(众数/数颜色),那就只能块速的做了。或者,如果能树套树但是出题人卡空间(如lxl),那也只能块速的做。
思想
其最主要的思想便是 平衡,设一个阈值,把两种复杂操作的复杂度平衡起来。
和中庸的思想类似
它其实也有分治的意思,把原问题分解成了一堆小问题。所以也可以认为分块是一种类似线段树的分治结构,如图(同样是lxlppt里的),是一颗只有三层的 \(B\) 叉树。
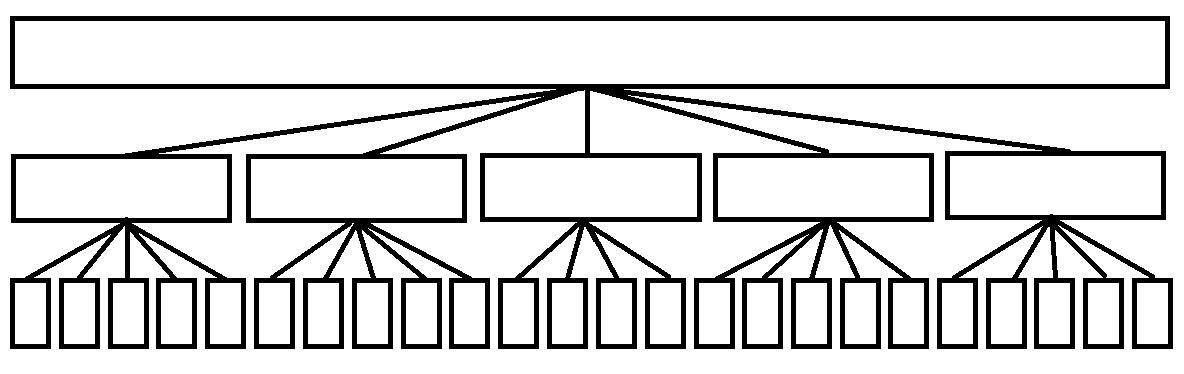
经典题:区间最小众数
如题,每次给一个区间,求出现次数最多的数是哪个;如果有并列最多的,输出数值最小的那个
loj的6285,洛谷的5048,都差不多这个题意(洛谷那个要求输出次数)
按照上述分块的思想考虑,对于整块,我们可以直接预处理出这一块内部哪个最多
但是我们有一堆整块要合并,咋办呢?暴力合并的复杂度似乎不太对(因为要合并整个 cnt 数组)
小 技 巧:当发现一堆整块要合并而不好合并的时候,可以把它预处理出来,复杂度 \(O(n\sqrt{n})\) 的
预处理一般就枚举块的区间 (有 \(O(\sqrt{n}^2)=O(n)\) 个),然后可以递推什么的
那我们考虑预处理出来,\(F(l,r)\) 表示第 \(l\) 个块到第 \(r\) 的块中出现最多的是哪个数,顺便再记一下出现多少次。
那查询的时候就把中间的整块,啪的一下做完了
那散块的答案咋更新呢?我们发现我们并不能很快的维护出整块里面的 cnt 数组。可以考虑这样:
假设当前最多 \(C\) 次。对于左边的散块,看看它右边(算自己)能不能有 \(C+1\) 个数,如果能有,就给 \(C\) 增加 \(1\)。右边同理。
这个 “能不能有 \(C+1\) 个数” 可以这么做,对于每种值,维护它出现的位置数组(开vector/用new动态申请),然后(以左边为例)看看它出现的下 \(C\) 个位置是否还在 \(r\) 之前即可。这样判断是 \(O(1)\) 的,预处理也是 \(O(n)\) 的,很快啊
记每个值的出现位置数组这个trick,在刘汝佳的蓝书中有提到,是一个很经典的trick,如果没见过没关系,见多了就知道了
那这样一来,总复杂度就是 \(O(n\sqrt{n}+Q\sqrt{n})\) 了。
总结:
-
分块之后,只有 \(O(\sqrt{n})\) 个块,因此我们可以对这些块做一些在线段树上不好做的操作,或者说是更加暴力的操作,从而更好的支持各种各样的功能
比如说我们可以直接 \(O(B^2)=O(n)\) 的记录块两两之间的信息
-
分块问题中,又要注意整块的处理,又要注意小散块的处理
-
当我们发现一个问题用线段树/树套树根本没法搞的时候,可以考虑sqrt tech
codechef FNCS
题目名称看成Chef and Cthulhu
我们发现这个题的修改十分阳间,询问十分阴间
此时可以利用分块中 平衡 的思想,去加快查询的速度
对于询问,我们直接在函数上分块。散块就暴力加一下,考虑能否块速的维护整块的和。
既然我们想块速维护,最直接的想法就是,记 \(fs(i)\) 表示第 \(i\) 块里函数值的和。
这里的fs并不是指flandre scarlet
考虑修改(看成是加操作)一个位置对一个块里的函数有多少贡献系数。这个可以直接预处理出来,对于一个块里面,我们用一些差分等区间加技巧,就可以求出 \(a\) 序列中每个位置对这一块的影响系数。设 \(co(i,p)\) 表示 \(p\) 位置对第 \(i\) 块的贡献,那我们单点修改 \(p\) 增加 \(x\) 的时候,枚举一个块 \(i\),把 \(x\times co(i,p)\) 加过去就行了。
现在还遗留下一个问题,对于散块,我们需要块速支持求区间和。事实证明树状数组的一个 \(\log\) 已经过不去了。
然而我们前面已经带一个根号了,这会还用啥树状数组啊,用sqrt tech:对 \(a\) 我们也分块,记一下块之间的前缀和,和每一块内部的前缀和,然后每次 \(O(\sqrt{n})\) 的修改,以及——\(O(1)\)查询!
分析一波复杂度
对于加操作:首先是去分块维护 \(a\) 的和,这部分是 \(O(\sqrt{n})\) 的;然后是去贡献一整块的函数,也是 \(O(\sqrt{n})\) 的
对于询问:整块是 \(O(\sqrt{n})\) 的遍历求和,散块是 \(O(\sqrt{n})\times O(1)\) 的求和,这里的 \(O(1)\) 是上面的块速求和
综上,复杂度是 \(O(m\sqrt{n})\) 的,一个 \(\log\) 都不带。
树状数组:别骂了别骂了
总结:
-
尽管分块结构是带根号的,但是当询问与修改的规模不同,需要特别快的支持其中一个,而另一个则允许更慢的时候,分块还有着特殊的意义
-
当我们发现一个操作阴间而另一个操作阳间的时候,我们可以使用分块,平衡二者的复杂度
如本题:我们把单点修改操作从直球的 \(O(1)\) 变成了 \(O(\sqrt{n})\) 的,而加快了区间求函数和的操作
树分块
首先分块的本质相当于是标记一些关键点,使得它们分布的比较匀称,点有 \(n/S\) 个,间距都在 \(S\) 以内,然后我们把点与点之间的间隔看成是“块”,然后再做散块和整块的处理。
这样,如果我们能在树上比较匀称的标关键点,那我们也可以实现树上的分块。对于一条路径,它肯定被一些关键点切开,然后和序列上一样,整块直接搞,散块暴力搞,就行了。
但是树上有两条路径,可能要考虑一些去重方面的问题,或者是更复杂的维护 —— 毕竟有四块散块。
我暂时只会这样一种分块方法:假设块大小是 \(S\),然后去标记关键点。每次找一个最深的,没被标记的点,如果它上面 \(S\) 个都没被标记,就标记它上面数 \(S\) 条边(即 \(S\) 级祖先)那个点。
这样一标记,显然点之间的间隔是 \(O(S)\) 的;标记一个点至少会让 \(S\) 个点再也无法标记,于是顶多有 \(n/S\) 个点,满足条件。
对于洛谷的板子题,就在路径的块上,维护区间的bitset;对于散块,就暴力加入bitset;然后bitset的count就是答案了。
莫队
这个再经典不过了。它利用分块的结构,优化区间移动的步数到根号。
那随便来几个经典题讲一下吧
bzoj 3809
我们发现不仅要数颜色,颜色还带了一个区间限制。
那我们肯定想维护一个 cnt 数组的前缀和。但是我们在莫队的过程中要不断的资瓷单点加,一共有 \(O(n\sqrt{n})\) 次加操作,而查询操作只有 \(O(m)\) 次。
此时,结合上一个题的想法:我们分块!我们可以块速的支持单点加,\(O(1)\);而查询就算变成 \(O(\sqrt{n})\),总复杂度也是对的,是 \(O(n\sqrt{n}+m\sqrt{n})\)。
具体的讲就是,我们直接维护这个 \(cnt\) 数组,并记一个数组 \(col(i)\),表示 \(cnt\) 数组的第 \(i\) 块里,有多少个位置非 \(0\)。
注意一下,\(cnt\) 和 \(col\) 都是设在值域上的数组
对于修改,直接在 \(cnt\) 数组上改,然后看看对 \(col\) 数组有没有影响,显然 \(O(1)\)
对于查询,先把 \(col\) 按整块加一下,然后散块暴力看看是否非 \(0\),算一算,显然 \(O(\sqrt{n})\)
然后就是套一个莫队,就做完了。
这里算是一个 trick,在莫队的过程中,我们也可以用分块来平衡它询问和加一个数的复杂度
Ynoi 2017 由乃的玉米田
这题是典型的,莫队+bitset
一般维护数种类,或者数之间的关系,用bitset可能会很好做
莫队之后,动态维护区间的数组成的bitset
对于减的查询,就把bitset给左移一下和自己求个就行了。对于加的查询,需要维护一个反过来的bitset,然后再求交 (其实这算是一种另类的卷积)
对于乘查询是最sb不过的,枚举因数,\(O(\sqrt{n})\)
除的查询则是这个题的精髓:根号分治!
这也算是一种平衡复杂度的方法。设两个数的商被要求为 \(d\),我们分类讨论
如果 \(d\) 比较大,大于 \(\sqrt{n}\),说明小的那个数范围不大,小于 \(\sqrt{n}\),暴力枚举一下就行了
如果 \(d\) 比较小,脑子一想,诶,不会做。
但是我们发现 \(d\) 的范围小,其实我们可以先暴力枚举 \(d\) ,然后 \(O(n)\) 的扫一遍。对于当前扫到的 \(a\),我们看一下上一个 \(a\times d\) 和 \(\dfrac{a}{d}\) (\(a\) 为 \(d\) 倍数)在哪,然后对于当前区间,看看它在不在左端点里面就行了。
至此,我们解决了四种询问。
总结:
-
莫队和bitset配合,能很好的解决区间的种类问题
如果不强制在线,它是区间数颜色的一种好做法之一,虽然那个可以主席树
-
根号分类讨论可以做到平衡复杂度
[Ynoi2016] 掉进兔子洞
果然练sqrt-tech还是要找ynoi
我们发现这个东西,其实就是要减去三个多重集的交。具体的说,对于同一种数,假设分别出现了 \(c_1,c_2,c_3\) 次,那它被删去的次数就是 \(min(c_1,c_2,c_3)\)
接下来问题便乘,要去三个多重集的交。
如果是三个集合的交那我们会做,三个bitset来&一下就行了
那如果是多重集,怎么做?
这里是一个神秘trick:min/max与交/并的转化
我们在证明min-max容斥的时候其实就用了这个转化,是一个很有用的转化,因为min/max的性质与交/并的性质其实是类似的
即,我们把一个数 \(x\) 看成是集合 \(1,2,3...x\),那 \(min\) 就变成了集合的交,\(max\) 就变成了集合的并
这题里相当于是求三个 \(cnt\) 数组的 \(min\),有很多位置;我们可以用计数排序里类似的思路,对 \(cnt\) 数组求一个前缀和,然后分配一下空间
然后就对三块区间分别做一遍莫队,最后求一个&就行了
然后注意到本题卡空间,所以可以把询问一万个分一组来做,一共要做10次;就当每次是一个新问题就行了,然后每次记得清空一下。这样其实会变慢,但是空间少 \(10\) 倍,是典型的时间换空间。
后记
感觉下午4,5点钟这个特别困的时候, 特别适合写blog, 毕竟打不动题
现在暂时还没学多少内容,只是简单的入门一下,东西少,抱歉qaq
其实我也是啥都干不动了,来写点blog总结一下,假装自己很努力
最后,
都2020年了,还有人考分块?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号