后缀三姐妹 笔记

目录

• 后缀三姐妹 笔记
  • 符号
  • 后缀数组 (Suffix Array / SA)
    • 基本定义
    • 如何求
  • 后缀树 (Suffix Trie)
    • 如何应用
  • 后缀自动机 (Suffix Automaton / SAM)
    • 基本定义&性质&简单证明
      • 自动机
      • 点的含义与性质
      • 后缀链接link
    • 如何构造
    • 如何应用
    • 填坑：建后缀树

后缀三姐妹 笔记

迫真字符串部：后缀の里技

符号

• \(\Sigma\) ：字符集
• 设 \(s\) 是一个字符串，从 \(1\) 开始编号：
  • \(|s|\)：串 \(s\) 的长度
  • \(s[l:r]\)： \(s\) 的子串 \([l,r]\)，\(l\) 和 \(1\) 取 \(\max\)，\(r\) 和 \(|s|\) 取 \(\min\)
  • \(s[p:]\)： \(s\) 从 \(p\) 开始的后缀
  • \(s[:p]\)： \(s\) 到 \(p\) 为止的前缀

后缀数组 (Suffix Array / SA)

基本定义

将所有的后缀拿出来排个序，得到的就是后缀数组。一般我们会存几个数组

• rk[i]：\(s[i:]\) 的排名

• kth[i]：排名为 \(i\) 的后缀从哪里开始

• height[i] （代码写作 ht[i]）：\(LCP(s_{kth(i)},s_{kth(i-1)})\)

前两个是最基本的，第三个拿来求 \(LCP\)，应用更广泛。

如何求

前两个：先求出来 \(rk\)，然后 kth[rk[i]]=i 即可

考虑求 \(rk\)：倍增法。每次的 \(rk[i]\) 为，\(s[i:i+2^k-1]\) 的排名。 取到 \(k=\log n\) 的时候，这个东西就是全部的排名了 （注意取子串这个操作对 \(|s|\) 取 \(\min\)）

现在我们已经求好了 \(k\) 的排名，要求 \(k+1\) 的排名。

那很简单，把 \(i\) 位置看作是 \(rk[i],rk[i+2^k]\) 组成的二元组，然后来一个双关键字的排序即可。

然后这样是 \(O(n\log^2 n)\) 的。太慢了。考虑用计数排序（鸡排） 优化掉它，就变成了 \(O(n\log n)\)

如何鸡排：

#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)

int cnt[N];
int a[N],tmp[N];
void chicken_sort()
{
	F(i,1,n) cnt[a[i]]++;
	F(i,1,n) cnt[i]+=cnt[i-1];
	D(i,n,1) tmp[cnt[a[i]]--]=a[i];
	F(i,1,n) a[i]=tmp[i],tmp[i]=0;
}

这个东西画一下就懂了，意思就是，某个东西出现了 \(cnt\) 次，那就给它分配 \(cnt\) 个空间，然后每次从后往前遍历，从后往前填充它现在应当所在的位置。

注意到两个“从后往前”方向一致，所以它是稳定的。

现在有两个关键字。可以先按一个关键字做一遍（稳定的）鸡排，然后用这个结果做第二遍鸡排，即可。

先想象一下两次鸡排怎么写，代码到最后给全。

你想看，就让你看个够啦

接下来考虑 ht 数组。考虑它的辅助数组：\(h\) 数组

\(h[i]\) 表示 \(i\) 和 \(i\) 排名前一位（\(kth(rk(i)-1)\)，后记作 \(pre(i)\)）的 \(LCP\)

\(h\) 数组有一个性质：

\[h[i]\ge h[i-1]-1 \]

证明这个结论之前，先考虑排好序的后缀有甚么性质

在排好序的后缀中，设排序结果为 \(s_1,s_2\cdots s_n\)，有：

\[LCP(s_i,s_j)=\min(ht_{i+1},ht_{i+2}\cdots ht_{j}) \]

显然可以想象出来

设它（\(LCP\)）为 \(k\)。那么 \(s_i,s_j\) 的 \(k+1\) 位一定不同，并且 \(s_i\) 的更小

想像一下排完序之后数组长什么样。每次相邻两个都是，前面若干相同，然后有一个不同，一定是变大的。

那么假设 \([i,j]\) 区间的变化中，有一次的变化落在了 \([1,k]\) 之间，那么 \([1,k]\) 组成的串的字典序就已经 严格 大于 \(s_i[1:k]\) 了，并且以后还会保持严格大于的状态。那么和我们假设的 \(LCP(s_i,s_j)=k\)，即他们前 \(k\) 个相同，就矛盾了。

于是 \([i+1,j]\) 的 \(ht\) 一定都 \(\ge k\)

那一定有一个 \(=k\) 吗？显然是有的：要不然 \(k+1\) 位不会有变化，那 \(LCP\) 就是 \(k+1\)，或者以上了，又矛盾了。

于是证毕。

然后回到 \(h\) 性质来。结合这个图来证明一下 \(h\) 的性质。

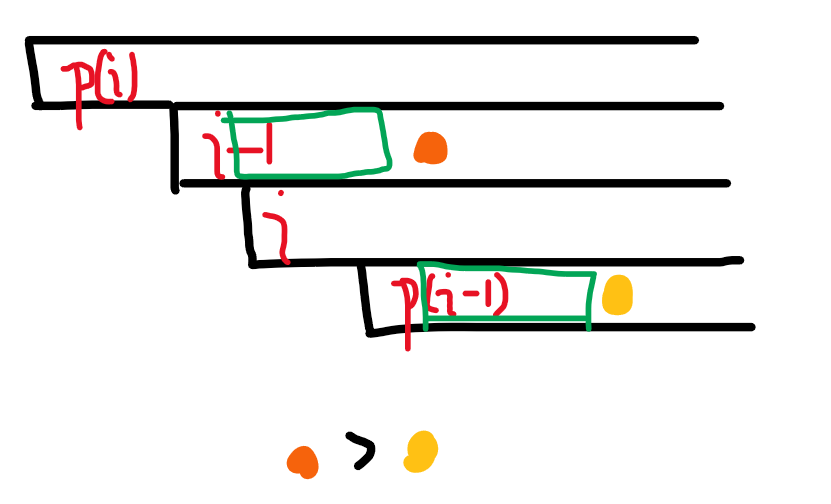
这里的每一个黑色方框表示 \(s\) 的一个后缀。

\(p(i)\) 就是 \(pre(i)\)，仅对这个图中有效。

2021.05.04：虽然我承认是我懒，但是没有数位板真的难受，饶了我吧

\(h[i-1]\) 就是 \(LCP(i-1,p(i-1))\)。然后现在我们同时拿掉第一个字符，得到两个绿色的串，长度为 \(h[i-1]-1\)。然后绿色的串后面分别是橙色，黄色的字符，橙色>黄色 （由于我们排好了序）

那么橙色就是 \(i\) 后面那个位置，得到 \(s[i:]\) 的字典序要大于 \(s[p(i-1)-1:]\)，并且 \(s[i:]\) 和 \(s[p(i-1)-1:]\) 的 \(LCP\) 就是 \(h[i-1]-1\)。

所以 \(s[p(i-1)-1:]\) 的排名在 \(s[i:]\) 的严格前面。那么，它的排名 \(\le\) \(p(i)\) 串的排名。由 \(LCP=min(ht)\) 的那个性质，我们知道 \(LCP(s[i:],s[p(i-1)-1:])\le LCP(i,pre(i))\)

原因很简单，由那个性质，$LCP\le $ 每一个 \(ht\)，而 \(LCP(i,pre(i))\) 就是 \(h[i]\)，即 \(ht[rk(i)]\)，是 \(LCP(s[i:],s[p(i-1)-1:])\) 的其中一个 \(ht\)。所以有这个 $\le $。

然后代换一下就有了，\(h[i-1]-1\le h[i]\)

有了这个性质有啥用呢？每次令 \(h[i]=h[i-1]-1\)，然后暴力找一遍，就可以 \(O(n)\) 的求 \(h\) 数组了。因为每次只会退一步，那一共只会退 \(n\) 步，那我们 ++ 的次数一定不会超过 \(2n\)，显然是线性的。

根据 \(h\) 就可以求 \(ht\)，然后再来一个 \(st\) 表，就可以支持：

\(O(n\log n)\) 的预处理，求出后缀数组的几个数组，以及支持 \(O(1)\) 查询后缀 \(LCP\)。

这大概是一个封装好的板子

struct node{int x,y,id;} t[N],t2[N];
int cc[N];
inline void chicken_sort()
{
	F(i,0,n) cc[i]=0,t2[i]=(node){0,0,0};
	F(i,1,n) cc[t[i].y]++;
	F(i,1,n) cc[i]+=cc[i-1];
	D(i,n,1) t2[cc[t[i].y]--]=t[i];
	F(i,1,n) t[i]=t2[i],t2[i]=(node){0,0,0}; // 这是普通的鸡数排序, 做两遍即可

	F(i,0,n) cc[i]=0,t2[i]=(node){0,0,0};
	F(i,1,n) cc[t[i].x]++;
	F(i,1,n) cc[i]+=cc[i-1];
	D(i,n,1) t2[cc[t[i].x]--]=t[i];
	F(i,1,n) t[i]=t2[i],t2[i]=(node){0,0,0};
}
class Suffix_Array
{
public:
	char tt[N];
	int kth[N],rk[N],h[N],ht[N];
	int st[N][22],lg[N];
	void Build(char s[])
	{
		F(i,1,n) tt[i]=s[i]; sort(tt+1,tt+n+1);
		F(i,1,n) rk[i]=lower_bound(tt+1,tt+n+1,s[i])-tt;
		// 直接排序一遍得到最开始的rk

		F(k,1,20)
		{
			F(i,1,n) t[i]=(node){rk[i],rk[min(n+1,i+(1<<(k-1)))],i}; // 双关键字
			chicken_sort();
			int tot=0;
			for(int l=1,r=1;l<=n;l=r)
			{
				++tot;
				while(t[l].x==t[r].x and t[l].y==t[r].y and r<=n) // 注意要处理一下相同的, 并赋以相同的rk
				{
					rk[t[r].id]=tot;
					++r;
				}
			}
			if (tot==n) 
			{
				break;
			}
		}
		F(i,1,n) kth[rk[i]]=i;

		F(i,1,n) if (rk[i]>1)
		{
			h[i]=max(h[i-1]-1,0);
			int p=i,q=kth[rk[i]-1];
			while(s[p+h[i]]==s[q+h[i]]) // 暴力找
			{
				++h[i];
			}
		}
		F(i,1,n) ht[rk[i]]=h[i];

		lg[1]=0; F(i,2,n) lg[i]=lg[i>>1]+1;
		F(i,1,n) st[i][0]=ht[i];
		F(k,1,20) if ((1<<k)<=n)
		{
			F(i,1,n)
			{
				st[i][k]=min(st[i][k-1],st[i+(1<<(k-1))][k-1]);
			}
		} // st表
	}
	inline int mn(int l,int r) // 求一下最小值就是区间LCP了
	{
		if(l>r) swap(l,r); ++l;
		int k=lg[r-l+1];
		return min(st[l][k],st[r-(1<<k)+1][k]);
	}

	inline void clear()
	{
		F(i,0,n) 
		{
			tt[i]=kth[i]=rk[i]=h[i]=ht[i]=lg[i]=0;
			F(k,0,21)
			{
				st[i][k]=0;
			}
		}
	}
}S;

后缀树 (Suffix Trie)

考虑把每个后缀都插入到 Trie 里。

然后这个东西太大了，点数太多。

发现它的叶子只有 \(n\) 个，所以很多都是单叉，只有最多 \(n-1\) 个点能是多叉的，把链缩起来即可。

其实这是一个建虚树的过程。

事实上我并不会只建一个后缀树，我只会拿 SAM 建后缀树。所以咕到 SAM 来讲。

如何应用

放在树上考虑，做一些dp，贪心，之类的

后缀自动机 (Suffix Automaton / SAM)

提示：本篇仅供个人复习用，新手想要更好的体验首选 oi-wiki

基本定义&性质&简单证明

自动机

自动机的定义：

简单来说，就是边上带一个字符作为权的有向图。顺着有向图的边走，可以到达一个点，把边上的字符连起来，就是这个点表示的状态。一个点的状态不一定是一个，可能是一个集合。

我们接触过的自动机，Trie 就算一个。

我们称一个自动机能 接受 一个串，当且仅当，我们按照这个串的字符，在自动机上走，不会没有转移可以走。否则称这个自动机 不接受 这个串。

自动机上走一条路径，把路径上的字符依次串起来，可以对应一个字符串（字面意思）。后面说是“对应的串”，“表示的串“等，都指这个串。

SAM 是一个点、边数量都是 \(O(n)\) 的自动机，并且它能且仅能接受串的 所有后缀。它是一个高度压缩的自动机，毕竟把 \(O(n^2)\) 个串用 \(O(n)\) 个点表示了出来。下图是一个例子，原串是 aabbabd

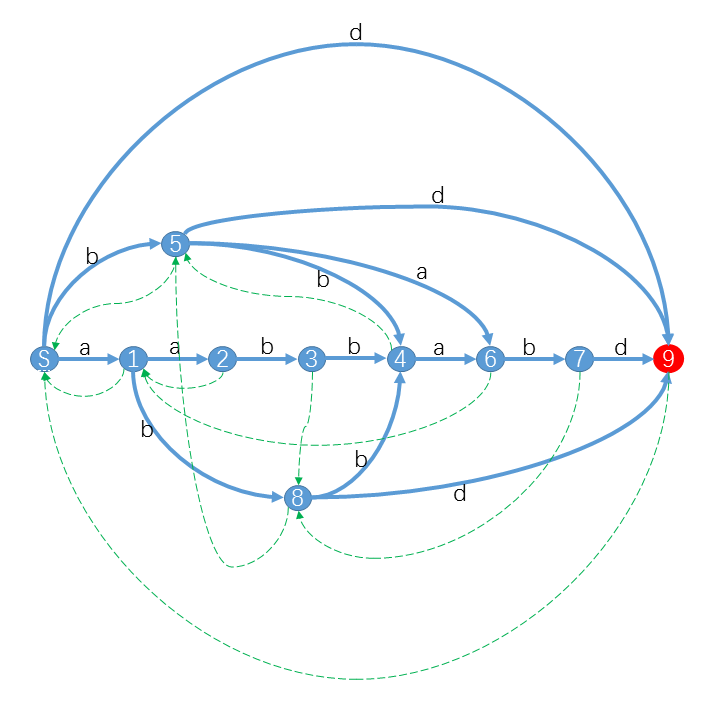
点的含义与性质

update 2021.7.21：以前写的是垃圾！！重新写！！

SAM是一个自动机，上面的任意一条路径对应着一个子串。由于它是一个DAG，所以从 \(S\) 走到某个节点 \(u\) 的路径并不唯一。于是，SAM上的一个节点 \(u\) ，它代表着很多个串，也就是 \(S\) 到 \(u\) 的所有路径所对应的串。

我们继续思考它的性质。一个点 \(u\) 对应着很多个串，但毕竟是同一个节点，它往后如何转移，都应该是固定的。比如说上面的那个例子：我们走到了 \(4\) 号点，虽然它对应了很多串（aabb,abb,bb），但是它后面的转移，比如走 \(a\) 边到 \(6\)，再走 \(b\) 边到 \(7\) ，这些是固定的，不管是以哪种方式走过来。

换句话说，一个节点对应的每个串，它“后面长什么样”，再换句话说，后缀，应该是都一样的。

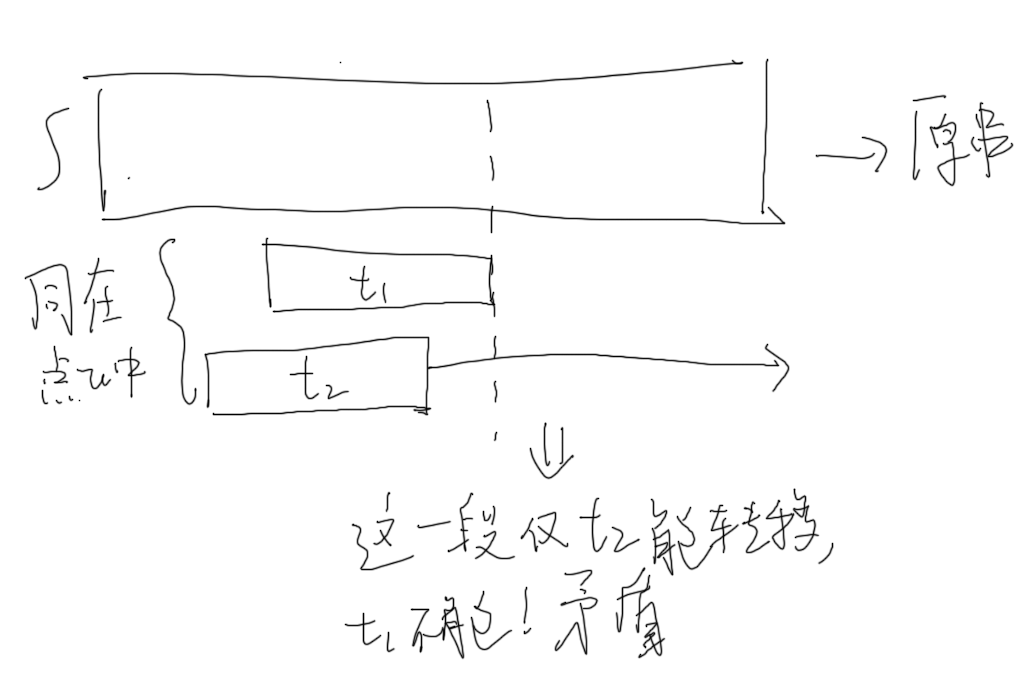
那我们这么思考，假设串 \(t_1,t_2\) 都是 \(u\) 节表示的串，会不会有下图这样，\(t_1\) 在某个位置出现而 \(t_2\) 没有？

不可能。假设 \(t_2\) 是靠前的那个，那 \(t_2\) 就会比 \(t_1\) 多一截转移边。而我们知道，从同一个节点出发的转移边都应该相同，矛盾。

所以，我们设 \(endpos\) 表示原串的某个子串出现位置的 右端点 集合。那一个节点对应的串，这个 \(endpos\) 集合应该是一样的。

为啥是右端点？因为我们要控制它们的 后缀 相同

如果是我们自己来设计这样的一个自动机，我们已经知道了一个节点的 \(endpos\) 集合相同。当然，考虑到效率问题，肯定要让节点和转移边的数量尽量小。那我们肯定不会把同一个 \(endpos\) 集合拆开来。于是，我们把所有子串按照 \(endpos\) 划分，相同 \(endpos\) 的子串放一个节点。

\(endpos\) 集合有两个重要性质，方便我们维护 SAM 节点的信息。

1. 对于两个串 \(a,b\)，二者的 \(endpos\) 集合要么没有交，要么一个是另一个的子集（这个当且仅当一个是另一个的后缀）

2. 如果 \(b\) 是 \(a\) 的后缀，二者 \(endpos\) 相同，那么 \(a\) 的长度为 \(|b|,|b+1|...|a|\) 的后缀，这些串的 \(endpos\) 集合均相同

道理很简单。

1. 不妨设 \(a\) 是那个大的。如果存在着后缀关系，那 \(a\) 一出现，\(b\) 必然出现，此时 \(endpos(b)\) 包含 \(endpos(a)\)；反之，若不存在，那 \(a\) 一旦出现，\(b\) 必然不会在同一位置出现，此时二者没有交集。
2. 随着串长度的减小，“出现”这个条件越来越松；于是 \(a\) 的后缀，随着长度的减小，\(endpos\) 的大小是非严格递增的 （后面>=前面）。在一个非严格的递增序列上，如果两个位置相同，那意味着中间这段都相同，于是这个性质也得证了。

那同一个节点 \(u\) 所表示的串，一定都是从某个串开始，然后不断的取后缀，并且长度是不断的-1，-1...

后缀链接link

既然我们知道了SAM的节点是什么样的，那如何构造呢？

假设我们构造好了前面，现在加入了一个新的字符 \(c\)。新增加的子串，一定是前面选后缀，后面加上 \(c\)。于是我们要对前面的这个构造好的串遍历它的后缀，然后再看看加入了 \(c\) 之后，\(endpos\) 集合的变化。

刚才提到，\(endpos\) 这个集合的大小，随着后缀长度的减小，呈现非严格的递增。那这些转折点，即，开始出现变化的位置，也显得比较关键。如果我们能找到这些个位置，那我们就可以把一个串的所有后缀全部串起来。

如下图，对于 \(p\) 结尾的前缀，\(u\)，\(v\) 是两个SAM节点，其 \(endpos\) 均包含 \(p\) 位置，而 \(v\) 的 \(endpos\) 更大。

如果我们能在 \(u,v\) 间连出一条边，然后 \(v\) 再连，再连... 全部都串起来，就能得到 \(S[1:p]\) 的所有后缀所对应的节点了！

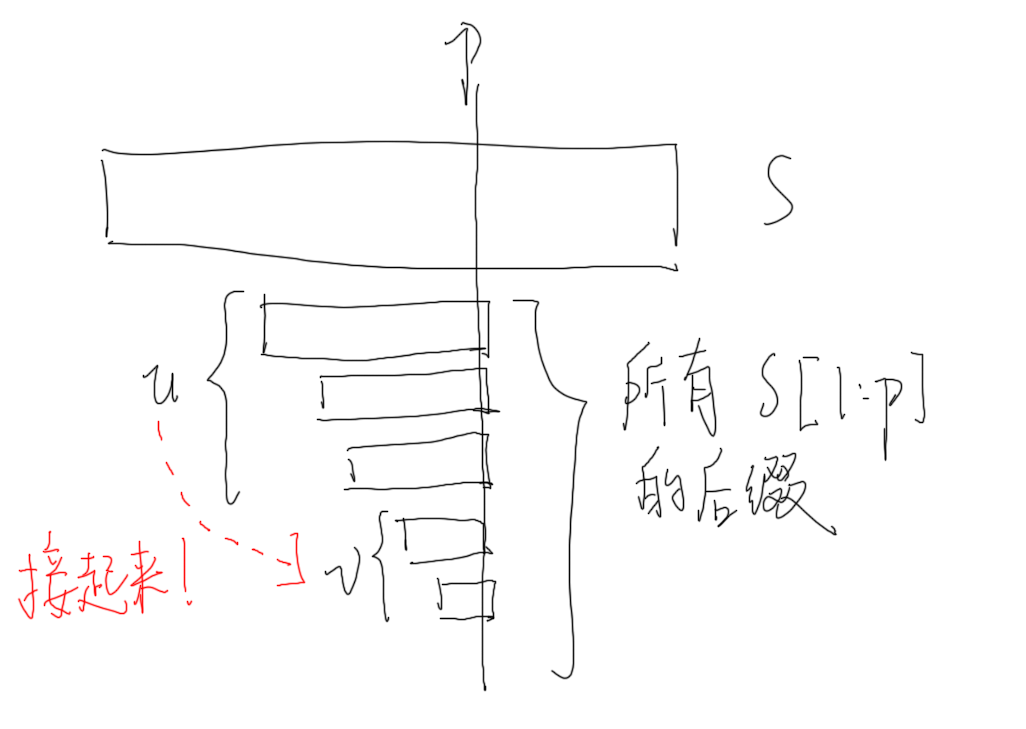
设 \(link(u)\) 表示 \(u\) 节点对应的这个 \(v\) 节点。形式化点讲，要找一个 \(v\) ，使得它的 \(endpos\) 集合包含 \(u\) 的，并且其最长长度 \(maxlen(v)\) 最大

感性理解：因为我们要串起来，所以需要找最“近”的，一点一点的串起来

比如说 abaab 这个串，abaab，baab，aab 的 \(endpos\) 都是 \(5\)，而 \(ab\) 是它们的后缀，但是 \(endpos\) 更大，是 \(\{2,5\}\)。

所以 abaab 对应节点的 \(link\)，就是 ab 对应的节点。

我们发现它有一个很好的性质：\(maxlen(link(u))=minlen(u)-1\)

然后我们就不用维护 \(minlen\) 了，直接取一下 \(maxlen(link(u))+1\) 即可。

代码里直接用 len 表示 \(maxlen\)

它还有另一个性质，每个点的 \(link\) 组成一颗树。

显然，因为 \(len\) 每次只会少，不会多，所以不会有环，而且显然会到 \(0\) ，所以联通，那就是树了

如何构造

考虑增量法构造：每次增加一个字符 \(c\)。假设前面搞好了 \(S[1:n]\) 的SAM，现在要把 \(n+1\) 位置的字符 \(c\) 加入。

显然有一个需要新增的节点：表示整个 \(S[1:n+1]\) 串的节点 \(cur\)。设 \(las\) 等于 \(S[1:n]\) 的节点，那么 \(len[cur]=len[las]+1\)，并且 \(las\) 到 \(cur\) 有一条 \(c\) 的转移边。

除去这条最trival的转移边外，还需要遍历上一个串的所有后缀，即，跳 \(link\) 链。如果发现没有 \(c\) 的转移边，也需要加上。

然后考虑求 \(link[cur]\)。我们需要找到上一次串的一个最长的后缀 \(x\)，使得 \(x+c\) 在前面出现过。那加上这一次加入后的出现，就至少两次出现；而我们全选这个串，显然只出现了一次；二者的 \(endpos\) ，肯定是前者包含后者；于是这个就是 \(link[cur]\) 了。

同样需要跳 \(link\) 链来遍历后缀，而且我们还要 \(x+c\) 出现过，也就是 \(x\) 有 \(c\) 这条转移边。找到最长的那个 \(x\) 即可，然后跳到它到 \(c\) 的转移边...这样就是 \(link\) 吗？

我们保证了 \(x\) 是 \(S[1:n]\) 的后缀，但是 \(x+c\) 所在的那个节点里面，最长的串可能比 \(x+c\) 更长，前面多出来一些不是 \(S[1:n]\) 后缀的部分，且这个东西的 \(endpos\) 集合不会（在加入 \(c\) 后）包含 \(n+1\) 位置，因为它前面有一小段不对

如下图，\(p\) 节点是 \(S[1:n]\) 的最长后缀，使得它有 \(c\) 这个出边；\(q\) 是它的 \(c\) 出边。但是我们发现 \(q\) 节点包含的串中还有更长的，即 \(maxlen(q)>maxlen(p)+1\)。此时 \(q\) 前面会多一段出来 （蓝色阴影），不能匹配到 \(S[1:n+1]\) 的后缀那里，而 \(q\) 包含 \(p\) 的那一部分（绿色线下方）能匹配。

沿着绿线切开，我们发现 \(q\) 节点下半部分的 \(endpos\) 包含 \(n+1\) 位置，而上半部分不包含。此时，\(q\) 节点不再是同一个节点，必须要裂开了，变成下图所示的红，黄两部分。

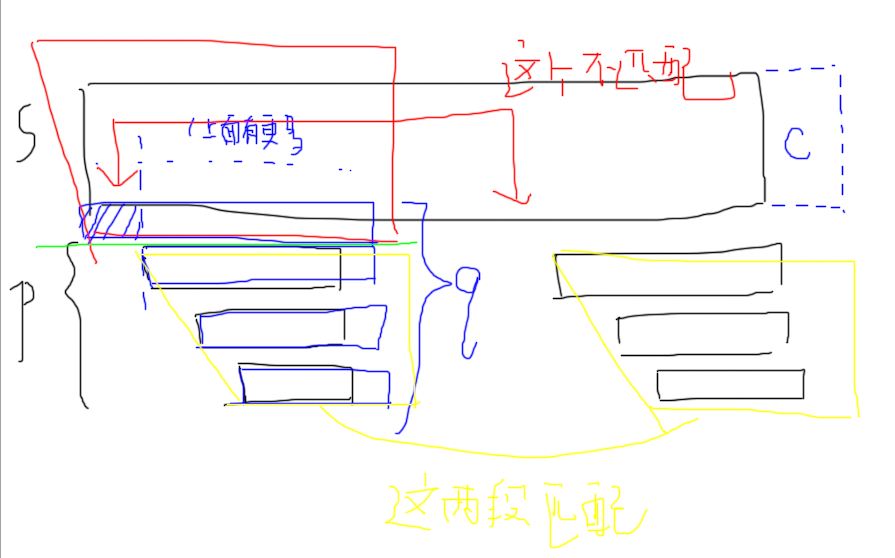
当然，如果 \(maxlen(q)=maxlen(p)+1\)，那就不用这么麻烦的拆节点，直接 \(fail(cur)=q\) 就行了。

这样我们就会求 \(fail\)，然后就有了一份构造 \(SAM\) 的代码

int nx[N][26],len[N],lk[N];
int tot=1,las=1;
int add(int c) // 0<=c<=25
{
    int cur=++tot; 
    cnt[cur]=1;
    len[cur]=len[las]+1;
    int p=las;
    while(p and !nx[p][c]) // 遍历后缀，加上 c 转移
    {
        nx[p][c]=cur; 
        p=lk[p];
    }
    if (!p) // 很 trival，但是别忘了
    {
        lk[cur]=1;
    }
    else
    {
        int q=nx[p][c];
        if (len[q]==len[p]+1)
        {
            lk[cur]=q;
        }
        else
        {
            int q2=++tot;
            len[q2]=len[p]+1; // len[q']=len[p]+1
            lk[q2]=lk[q]; F(i,0,25) nx[q2][i]=nx[q][i]; // 复制其它的
            lk[cur]=q2; lk[q]=q2; // 搞一下 link
            while(p and nx[p][c]==q) // 改一下转移
            {
                nx[p][c]=q2; 
                p=lk[p];
            }
        }
    }
    las=cur;
    return cur;
}

如何应用

现在你有了一个有向无环图，其中所有的路径对应了所有的子串。

那可以用拓扑排序来搞很多问题。

然后利用 \(link\) 树的性质，每个点的 \(endpos\) 集合其实就是它 \(link\) 树上子树里的并。线段树合并可以轻松搞出来这个，然后就可以用 \(endpos\) 集合来干很多好事了。

以及，可以基于 \(link\) 树跑 dp，也是常见套路。

还有，根据 \(link\) 树，跑一遍线段树合并，即可将 \(endpos\) 集合显式的存储在线段树上，这还是很有用的。

还有一种trick，就是对于SAM的每个节点分别考虑计算，可以解决一些形如 “有多少本质不同的串满足...条件” 的问题

填坑：建后缀树

反过来跑一遍SAM，得到的 \(link\) 树就是后缀树

证：

考虑后缀树上的一个分叉：\(u\) 分裂成了几个儿子 \(v_1,v_2...v_k\)

那么显然 \(u\) 出现了 \(k\) 次，但是儿子们的出现次数都只有 \(1\)次。造成这个东西的原因就是，出现次数不一样，那也就是，\(endpos\) 集合不一样。所以它就是一个 \(link\) 的关系。

考虑在原串中跳 \(endpos\) 集合，得到的东西是一个前缀的所有后缀。

后缀树上的节点，是一个后缀的所有前缀。

所以反过来建SAM即可。