2021CT03 Contest#9 降智场
A. Graph
题意
对一个任意图，做到下面两件事情之一：
- 3-染色。 即，给每个点一个1~3的颜色，使得相邻的点颜色不同
- 删掉一个奇环，使得图仍然连通
图的点，边数 \(n,m\le 3e5\)
做法
先搞一个DFS树来。按照如下规则：
一边DFS一边给点黑白染色。第一个点染白色，然后交替。
对于白点，就直接跑正常的DFS；对于黑点，我们预先把它没遍历过的邻居全部加入到生成树中（标一下vis），然后再DFS
把这些树边删掉，看看有没有奇环。这要是有，就直接把这个奇环删掉，那肯定连通。
否则，非树边不构成奇环。
此时，由于我们特殊的DFS规则，黑点与黑点之间没有非树边。那么非树边只有黑-白，白-白。
黑-白的非树边显然不用管（已经不同了），只需要考虑白-白。
非树边不构成奇环，说明构成二分图。那我们对白色点再跑一遍01染色，是“1”的那些点我们把它变成 “灰色”。
然后白-白的非树边也解决掉，此时的每条边两边的颜色都不同了，而且仅用了三种颜色。
B. sequence
题意
长度为 \(n\) 的序列，每个位置的颜色在 \([1,m]\) 中均匀独立随机。求最长的一段同色段，长度，的期望。
\(n\le 3e6,m\le 1e8\)，膜大质数。
做法
（来自机房大佬的做法）
机房大佬：雅礼扛把子 zxyhymzg！
期望 \(E(len)\) -> \(\sum P(len\ge x)\) -> \(\sum 1-P(len\le x)\) 。考虑计算这个
然后咱们控制每一段都不超过 \(x\)。考虑 \(f(i)\) 表示前 \(i\) 个，每一段同色长都不超过 \(x\) 的方案数。
脑子想一想，得到递推：
枚举上一段的结尾 \(j\)，从 \(j+1\) 到 \(i\) 都染一个色；不能和上一段相同，所以乘 \(m-1\)
设 \(f(0)=1\)。最后的答案要乘一个 \(\dfrac{m}{m-1}\)，因为第一段我们其实有 \(m\) 种，但是这样递推会被认为是 \(m-1\) 种。
然后我们注意到这个转移有一个区间求和，考虑前缀和 \(s(n)=\sum\limits_{i=1}^{n} f(i)\)
考虑它的组合意义，相当于我们从 \(0\) 开始跳，\(m\) 种方法跳一个，\(1-m\) 中方法跳 \(x+1\) 个，要跳到 \(n\)，的方案数。
枚举跳了多少次 \(x+1\) 个，复杂度是调和级数。然后瞎几把搞一搞就啊掉了。
C. walk
题意
数轴上有 \(n\) 个餐馆，第 \(i\) 个的位置在 \(i\)，其中有食物，质量为 \(a_i\) 。一人在数轴上走，从 \(0\) 开始，初始质量是 \(1\)，有一个能量值 \(x\)。他每走一个单位长度，消耗的能量（数值上）等于当前质量。可以随便走（可以经过任意点任意次），并且任意选择吃不吃，但是同一个餐馆只能吃一次。
现要从 \(0\) 出发，走一圈并回到 \(0\)，且保持能量值 \(\ge 0\)。问最多能吃多少质量食物。
\(n,x\le 10^6\)
做法
首先我们发现，如果我们确定了要吃哪个集合，肯定是在 \(1\) 的质量下先走到最远的地方，再一路吃回来。
为啥？因为吃一家餐馆对能量消耗的贡献等于，吃完它之后走了多长才回去，乘以 \(a_i\)。那对于每家餐馆我们肯定希望吃完尽快回去，于是都放在后面吃，最优。也可以用反证，把餐馆放到前面去吃，走的路更长，消耗更多，更劣。
然后设 \(f(i,j)\) 表示，到达最远点后折返的路上，折返到 \(i\)，当前吃的质量和为 \(j\)，消耗的最少能量。如下图。
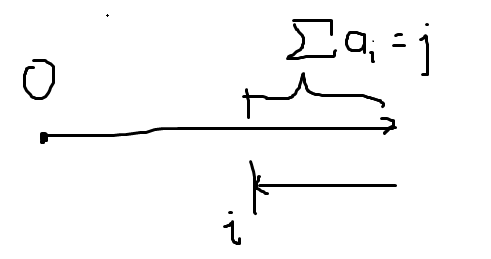
然后我们发现，这个 \(j\) 对以后的贡献，至少得有一个 \(j\times i\)。于是这个 \(j\) 就要 \(\le x/i\)。
然后我们又惊喜的发现，枚举这个 \(i\)，再枚举这个 \(j\)，复杂度调和的。
然后我们就又惊喜的过了。
总结
-
不要被题目的奇奇怪怪的外表迷惑，冷静一下，从本质入手分析问题
-
推着推着式子不要推的太上头，时不时跳出来看一下，现在是否已经能做了
如我考场上做 T2,T3 的时候，都想到了和正解一样的 dp（作为其中一个可能思路之一），但是我没看出来直接调和级数就能A掉了，两个题都因此与正解失之交臂
-
T1是真的妙妙题！！！
-
并不一定需要死磕一个思路，试试别的几个思路，是否同样能做
比如我T2就一直想着优化我那个 \(O(n^2)\) 的做法，而忽略了我随手写在纸上的那个递推式，小小优化一下，就能成为正解
后记：T2的神秘 \(O(n^2)\) 做法
一上来的转化同。现在变成限制 \(\le x\) 咋做。
\(f(i,j)\) 表示，到 \(i\)，后缀的最长的同色段长度为 \(j\)，方案数。对于 \(x\) 的限制，只要控制所有的 \(j\) 都 \(\le x\)，把 \(>x\) 的忽略，即可。
然后我们发现它有两种转移，\(f(i,j)\rightarrow f(i,j+1)\)，\(f(i,j)\times (m-1)\rightarrow f(i+1,1)\)
设 \(i\) 这个是“行”，\(j\) 这个是“列”。考虑两行之间的差异：下一行相当于上一行整体右移一位，然后把上一行的和 \(\times (m-1)\)，放在下一行的第一个。如果这样一位移，有超出 \(x\) 的，手动设为 \(0\) 即可。
然后我们把序列反过来，相当于要求支持：后面加数，前面删数，动态维护和。用队列维护即可。对于一个 \(x\) 是 \(O(n)\) 的。
讲这个的原因是我觉得这个思路也挺妙的，用队列直接维护dp数组，而不是常见的单调队列来优化dp转移。
