笔记 dp套dp
笔记 dp套dp
本篇侧重 理解。
从本质入手
dp的本质: 我们有一个要解决的问题，把问题分成若干步(dp的阶段), 每一步都有一个状态表示(dp的状态)，然后考虑状态间的转移。dp把问题通过某种顺序解决，使得我们可以 不记录 一些东西，而只记录我们关心的东西，以压缩我们描述状态用的东西
简单的说，就是我们把研究的问题的特征打包变成一个节点，节点连成DAG（通常），然后我们在DAG上拓扑的跑，就是dp的转移。
进一步思考
现在有一个能dp的问题，给定一个答案，求有多少种问题，使得输入它能得到给定的答案。
答案不一定是一个简单的数
首先我们必做的一件事情是，把这个问题的dp搞出来 （这个不搞后面咋搞）
接下来，能得到“答案”，还能如何变形？可以想到，把它变成能得到（内层dp的某一些） “状态”/“节点”
一拍脑袋觉得很有道理，接下来我们就有了设计外层dp的大方向：我们用和内层dp类似的方式拆解原问题，但是在每个阶段里，我们不去求答案，而是算有多少种输入能使得内层dp的值，长成某个我们想要的样子。
那外层dp的大概样子就是 \(f(U,P)\) 表示，内层dp考虑到 \(U\) 节点，我们要研究的（若干个）内层dp值（打个包）是 \(P\) ，的方案数。
为啥要考虑内层dp的节点？
- 因为我们和内层dp一样拆问题，就比如序列问题，内层dp是一位一位考虑，那我们外层的dp也一位一位的考虑，这时候我们的状态里就会和内层dp一样，有一个当前位置 \(i\)。
为啥我们要可能研究不止一个内层dp值？如何打包？
- 这个看内层dp的转移，如果要用到很多前驱dp值，那我们可能就要把一些dp值，比如说一行的dp值，给打包一下
- 打包方法最常见的就状压吧，其它的方法和状压也差不多，比如可能会有三进制状压之类的
检验真理
来点实践。
bzoj3864 Hero meet devil
给定一个串 \(S(|S|\le 15)\)，和一个 \(m\)。对于 \(k=0...|S|\)，要求有多少串 \(T\) 使得 \(|T|=m\) 且 \(LCS(S,T)=k\)。（这里LCS是子序列）
考虑LCS的dp，\(f(i,j)\) 表示 \(LCS(T[:i],S[:j])\)。这个显然可以转移，但是我们发现更多性质，就是 \(f(i,j+1)\ge f(i,j)\)，但是 \(f(i,j+1)\le f(i,j)+1\)。这两个都很显然，但是这代表 \(f(i,*)\) 的差分数列就是个 0/1 数列。
那我们就可以压了（注意到 \(|S|\le 15\)，显然可以压）。根据上面那一套思想，我们外层 dp 就这么设计：
\(f(i,M)\) 表示 \(T\) 到 \(i\)，这一行的内层dp数组做差分后压缩一下为 \(M\)，的方案数。
你可能会问，原dp中的j哪去了。 注意到我们直接把一整行打包了，所以这个j就没了，并且我们转移的时候是直接一整行转移的。
接下来我们考虑 \(T\) 到 \(i+1\)，加了某个字符。但是加上字符的变化，可以推一下，和 \(i\) 并没有关系，只和这一行的 \(dp\) 状态 \(M\) 有关。那我们可以很容易的从 \(f(i,M)\) 转移到 \(f(i+1,M')\)，最后随便统计一下就得到答案了。
TopCoder StringPath
给定两个长为 \(n+m-1\) 的串 \(A,B\)，问有多少个 \(n\times m\) 的字母矩阵，使得它恰好存在两条从左上到右下的路，一条的字符连起来是 \(A\)，另一条是 \(B\)。
同样用类似的套路，先考虑内层dp。
内层的dp是用一个二维的 \(dp[i][j][2]\) 记录到 \((i,j)\) ，是否能匹配 \(A/B\) 的前 \(i+j-1\) 位。
接下来考虑外层dp。就是考虑有多少个字符矩阵能到达某个内层dp的状态。内层dp的值我们发现它就是两个0/1，果断状压。
然后我们和内层一样，按枚举坐标 \((i,j)\) 考虑，并想怎么转移到 \((i,j+1)\)。我们发现这个东西的转移和左，上有关，并且还要可延续（即不能只记录它的左，上），所以我们压0/1压的是轮廓线，一条轮廓线存 \(m\) 个，而因为有 A,B 两个串，所以要存两条。
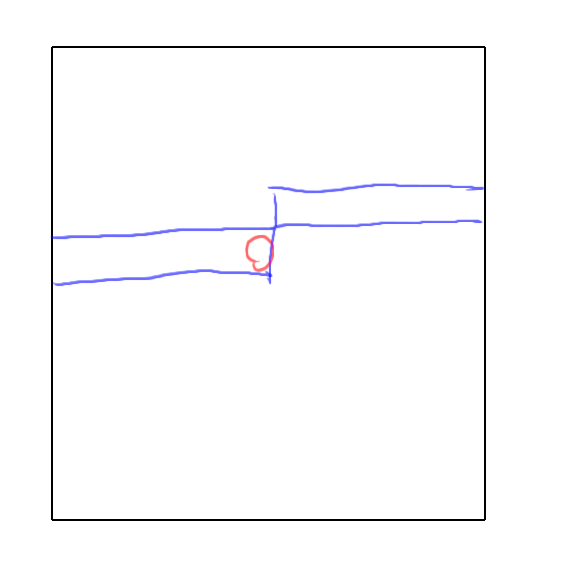
这里有个小细节，这个轮廓线应该是包含 \((i,j)\)，即 \((i,j+1)\) 头上的那条轮廓线，如下图，如果红色表示 \((i,j)\)，那我们记录的轮廓线是蓝色这一带。
实现的时候，我们直接拿状压的bitmask的（从低到高）第i位，表示轮廓线从左到右的第 \(i\) 个，而不是从上面开始数，一直顺序记到 \((i,j)\) 为止
也就只有我这种傻逼会想到后者这种阴间记法吧
这样我们就有了外层dp的状态，\(dp[i][j][A][B]\) 表示到 \((i,j)\) 位置，内层的dp的值的轮廓线状压起来是 \(A,B\)，有多少种。根据内层dp的轮廓线，很方便转移。然后这题就没了，复杂度 \(O(nm2^{2m})\)。
总结
dp套dp，它就是在原来的dp转移DAG上dp。
尽管我大概懂了它是个什么东西，但是我练的还太少，写题不够熟练
看提交记录里面一堆WA就知道了
