回文自动机 笔记
基础题型
给你一个字符串,对于每个前缀,求该前缀中有多少前缀不同的回文子串。定义一个回文子串的权值为:长度乘以出现次数。对于每个前缀,也请你求出最大的回文子串的权值是多少。
回文自动机(又名回文树)是干啥的
众所周知,在TRIE树上,每个节点表示一个字符串,字符记录在边权上。连一条边表示在这个字符串后面加上一个字符。
那么,回文自动机是怎么弄的的?连一条边,表示在这个字符串前后各加上一个字符。比如某个父亲的字符串为"aba",连了一条权值为'c'的边到儿子,儿子的字符串就是"cabac"。
然后要注意一点,回文自动机有两个根。其原因很显然,因为一个父亲以下的字符串长度的奇偶性不会改变。所以,两个根分别记录奇数长度和偶数长度的回文串,名字就叫奇根和偶根。偶根很好理解,表示一个空串,其长度为\(0\)。那么,奇根怎么办呢?仔细一推,单个字符长度为\(1\),其父亲的长度为其长度\(-2\),也就是说,奇根表示的字符串长度为\(-1\)?!
没事,\(-1\)就\(-1\),只不过是为了方便计算罢了。实际实现中,考虑到空间问题,我们并不会实际记录表示的字符串,只是记录一个长度\(len\)。那么,只要让这个点的\(len=-1\)即珂,一点问题都没有。
fail指针
精髓(准确来讲,是每个自动机的精髓)。对于一个节点,它的\(fail\)指针是指:除了自己之外,LPS(Longest Palindrome Suffix,最长回文后缀)所对应的点。
如果你仔细咀嚼了这句话,那么你会想这样一个问题:除了自己之外的最长回文子串一定在树上能找到吗?
证明fail一定在树上能找到
(如果您能自己证明,请跳过这段)
设当前节点表示字符串\(s\),\(fail\)指向的节点所对应为\(f\),\(f^t\)表示把\(f\)反过来,\(|f|\)表示\(f\)的长度,如图所示。
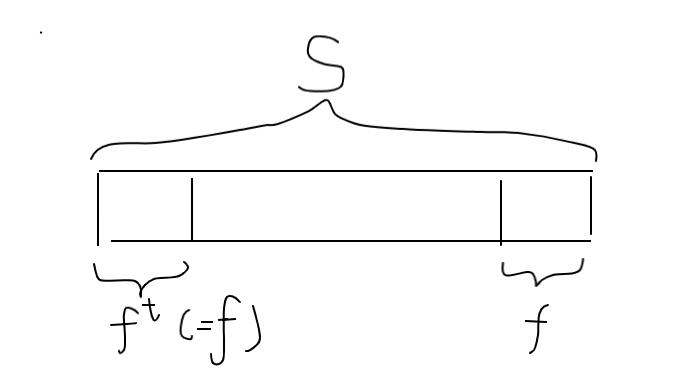
由于\(S\)是回文串(根据定义),\(S\)的前缀\(|f|\)个字符串和后缀\(|f|\)。\(S\)和\(f\)都是回文的,非常容易证明,\(S\)的\(|f|\)个前缀和这么长的后缀是一样的。
那么,\(f\)在后面出现一遍,就说明在前面也出现了一遍。由于我们是从前往后加入到树上的,所以这个串一定能找到。
证毕 \(\blacksquare\)
如何构建
上面讲了一下,我们是按照从前往后的顺序插入\(s\)的每个字符的。对于插入第\(i\)个位置,我们的任务是找到其\(LPS\),并把它插入到树上的正确位置。那么,如何找到呢?
等价一下,这个节点满足:
- 它是i-1位置的一个回文后缀
- 它左右字符相等,都是\(s[i]\)
对于满足条件1,我们记录一个\(last\),表示\(i-1\)插入在了树上哪个位置。(当我们插入完\(i\)的位置的时候,我们令它为我们找到的位置,即珂维护)
然后\(last\)显然就是\(i-1\)的一个回文后缀。但是我们要找到所有的回文后缀,那没问题,我们不断的跳\(fail\)即珂。
然后还要满足条件2。设现在我们跳到了点\(cur\),这个点上的长度值为\(len(cur)\)。只要判断\(s[i]==s[i-len(cur)-1]\)即珂。如果满足就退出,不满足就\(cur=fail(cur)\),继续循环。
关于\(fail\)的维护:很简单,和上面找到父亲的过程只差一个\(cur\)初始值的区别。因为\(fail\)指针要满足不等于自己,所以,\(cur\)的初始值,不是\(father\),而是\(fail(father)\)。和找到父亲的步骤还有一点点不同,就是最后找到一个\(cur\)满足\(s[i]==s[i-len(cur)-1]\)的时候,返回的不是\(cur\)而是\(cur\)的边权为\(s[i]\)的儿子。这里还有一个至关重要的细节要注意,先求出fail指针,才能连边。代码中会提到。
那么我们来举一个例子。我们要构建的字符串s="bilibili"。
初始化,构建奇根和偶根。红色是奇根,绿色是偶根。特殊地(忘了讲了),奇根和偶根的\(fail\)指针(黄色)互相指向对方。
第一步,插入位置\(1\)。默认是插入到\(0\)上,失败了再跳\(fail\)。我们发现,\(s[1]!=s[1-len(0)-1]\),于是跳了\(fail(0)=1\),然后显然满足了。我们还发现,此时还没有节点,便新建一个节点(编号为\(2\)),把它接在奇根(\(1\))下面。跳一下\(fail\),发现\(fail\)是\(0\)(显然)。由于很多节点的\(fail\)都是\(0\),这些边我就不连了(为了看起来美观)。效果图:
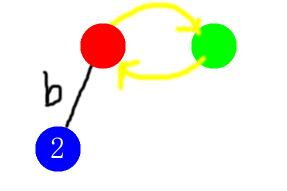
时间关系,我们不仔细看每一个位置的插入过程,直接跳到第\(5\)个位置的插入。这之前的图建出来长这样:
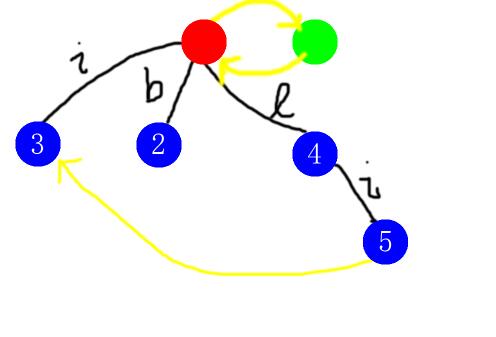
第五步,插入位置\(5\),此时前缀为\(bilib\)。默认插入在\(last\)上,也就是编号\(5\)的位置。我们一下就满足了条件,所以我们的确要接在\(last\)下面。求一下\(fail\)指针,先到\(fail(5)=3\)试一下,发现,不行。然后跳到\(fail(3)=0\)试一下,还不行,跳到\(fail(0)=1\)再试一下,行了,返回\(1\)的边权为\(s[i](='b')\)的儿子,也就是编号为\(2\)的节点。完成之后,图长这样:
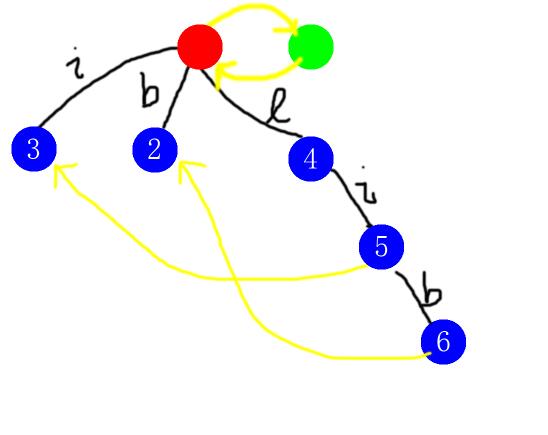
(跳过114514步)
最终完成图:
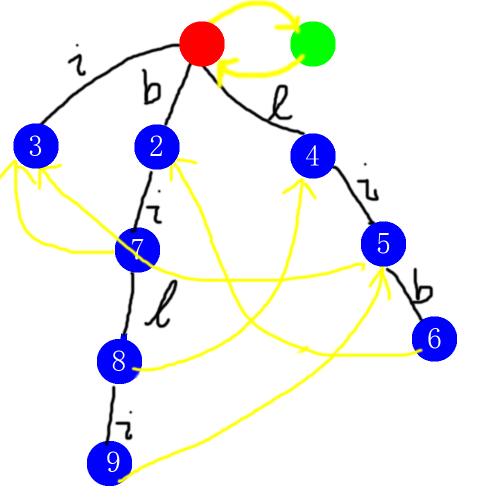
然后我们这就构建好了一个回文自动机。
代码
class Palindrome_Tree //我喜欢写面向对象
{
public:
char s[N];
struct node
{
int len,fail;
int ch[26];
}t[N];//保存一个节点
node& operator[](int id){return *(t+id);}
int last;
int cnt=1;//上一次插入在哪
void Init(char ss[N])
{
FK(t);
strcpy(s+1,ss+1);
t[0].len=0;t[0].fail=1;
t[1].len=-1;t[1].fail=0;//len=-1!!!!!
//注意:fail是互相指的
last=0;//开始默认接在0上,后来就接在last上,不行就跳fail
}
int Getfail(int fa,int pos)
{
int cur=t[fa].fail;
for(;s[pos]!=s[pos-t[cur].len-1];cur=t[cur].fail); //不行就跳fail
int id=s[pos]-'a';return t[cur].ch[id];//返回fail的儿子,记住藤野先生的话
}
void Insert(int pos)
{
// printf("Insert %d\n",pos);
// 方便理解用
int cur=last;//注意初始值
while(s[pos-t[cur].len-1]!=s[pos])
{
cur=t[cur].fail;
}//同上,不行就跳fail的过程
int id=s[pos]-'a';//当前字符
if (t[cur].ch[id]==0) //如果还不存在这个节点
{
++cnt;//新加一个节点
t[cnt].len=t[cur].len+2;//len+=2,显然
t[cnt].fail=Getfail(cur,pos);//求出fail
t[cur].ch[id]=cnt;//次序关键!先求fail,再连边
// printf("fail[pos]=%d\n",t[cnt].fail);
}
last=t[cur].ch[id];
}
}T;
应用
我们讲了这么多,来解决些实际问题。
-
本质不同的回文串个数
每个点(除了奇根和偶根)都一一对应一个本质不同的回文串。只要输出\(cnt-1\)即珂。(应该是点数-2,但是由于我是从0开始算点的,所以-1才是正确的) -
每个回文串的个数
每个点维护一个值\(cnt\)(重名了,但是因为命名空间不一样,写在struct里,所以不会报错)。然后插入一个点时,找到它所在的树上位置,该点上\(cnt++\)。最后再\(cnt[fail(i)]+=cnt[i]\),i从\(n\)到\(1\)。和\(KMP\)中计算每个前缀出现的次数是类似的原理。
尝试一下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号