线段树历史最值问题
感觉学一遍历史最值,大大加深了我对lazytag与pushdown的理解
WARNING:草图警告,字丑警告,灵魂画师警告
明确一些基本概念
-
lazytag:主体思想就是我把一个东西搁在这,要用的时候再拿出来
-
一个点上维护的lazytag是:当前节点的 待进行的操作的和 。这里的“和”指若干操作的合并等效。
操作可以是各种各样的,比如 \((\times a,+b)\) 是一个可合并的操作,(+a,对b取max) 也是
-
pushdown在干的事情是: 把父节点的操作序列接在儿子节点的序列之后
(—— He_Ren的题解)(前排膜He_Ren!!!)
最基本的入手:只有加减
第一想法:历史最大值不就是max的max么,打一下tag,然后用当前最大值更新历史最大值不就行了?
然后你会发现这个tag不能实时更新(因为待进行的操作要合并,然后一块被处理),万一你加了114514再减了1919810,被合并成一个tag (-1805296),那就忽略了+114514这个历史最大值。
如何在不增加复杂度的情况下把它变得不lazy呢?
来画图图~ (灵魂画师上场)
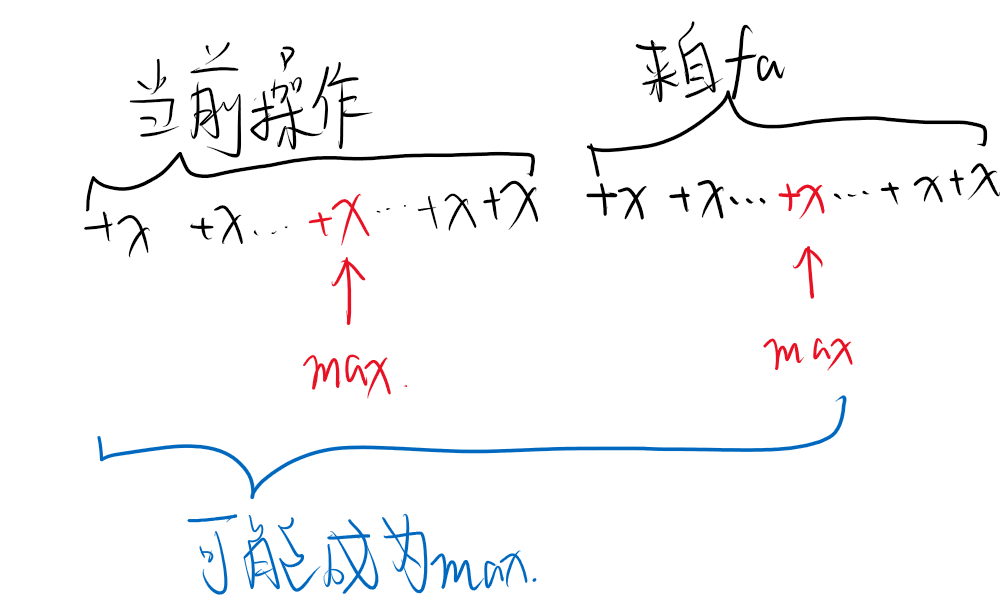
如图,当前节点的操作序列中,某一个位置(标红)达到了历史最大值;然后父亲给它续上了一些操作在后面。
如果它的历史最大值要变化,那肯定是后面带来的变化(显然)。操作进行到后面,前面的操作肯定都做过一遍了,所以有一段前缀是不变的,就是当前节点所达到的最大值。
而后面还有一段,我们要它最大。此时我们意识到,我们需要维护一个东西:lazytag的历史最大值 (记为mxtag)
由于lazytag是按时间顺序依次做的,所以相当于是 最大的前缀和
然后我们发现这个东西也可以更新:父亲续上了一些操作后,当前节点的mxtag更新的部分,也只是在后半段。用当前的操作的和 (即普通的lazytag)加上父亲的mxtag来更新即可。
可以得到一小段代码:
(简记lazytag为tag,mxtag同上;历史最大值为hmx,普通的最大值为mx)
(代码中有“h”前缀的代表历史最大值)
void addone(int ix,int ad,int admx)
// ix: index, 线段树上的编号
// ad: 来自父节点的加法操作的和
// admx: 父节点的加法操作达到的历史最大值
// 这俩就是父亲的 tag 和 mxtag
{
hmx[ix]=max(hmx[ix],mx[ix]+admx);
mxtag[ix]=max(mxtag[ix],tag[ix]+admx); // 注意要先更新两个历史最大值, 因为它俩要用mx和tag
mx[ix]+=ad; tag[ix]+=ad;
}
带上覆盖一块
考虑同一个区间中,有若干 +x 覆盖x +x 覆盖x ... 的操作。(相邻同类操作合并了)
然后从第一个覆盖开始,就都可以看成是覆盖了。很显然,都变成相同了,再整体加减,还是相同的。覆盖为 \(c\) 之后再加上 \(a\),等价于覆盖成 \(c+a\)。
那我们的操作就合并成 (+a,覆盖为c) 的形式,代码里写作 ad,cv(对应历史最大为admx,adcv)。
tip:做(较复杂的)题时务必要 明确 维护的(比较绕的)变量的含义
比如这里,最好先把 a,c 的严格含义用注释写一下,或者写在草稿纸上,然后再码
但是这个覆盖不一定有,所以要另开一个vis表示是否有覆盖操作,然后分类讨论。这里讨论有覆盖的情况,没覆盖就是直接对前面的加法做操作就行了,很trival。
我们要把父亲的形如 “+...+...覆盖为...覆盖为...” 的操作接到儿子后面。我们分两批,先接加法,然后把覆盖接过去。画图图~
(此处用圈圈里的等于号表示赋值,因为:=不好手写)
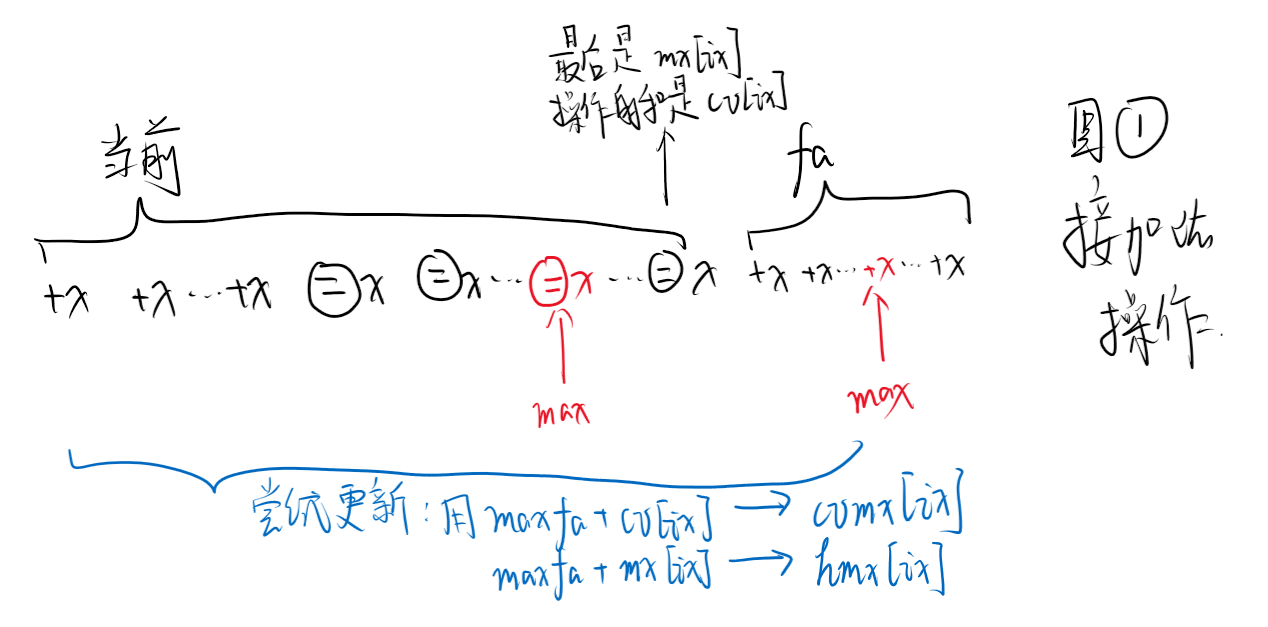
上面黑字:最后(的结果)是 mx[ix],操作的和是cv[ix]
下面蓝字:尝试更新:
maxfa+cv[ix] -> cvmx[ix]
maxfa+mx[ix] -> hmx[ix]
maxfa 在代码中就是 ha,表示父亲节点的加操作的历史最大值
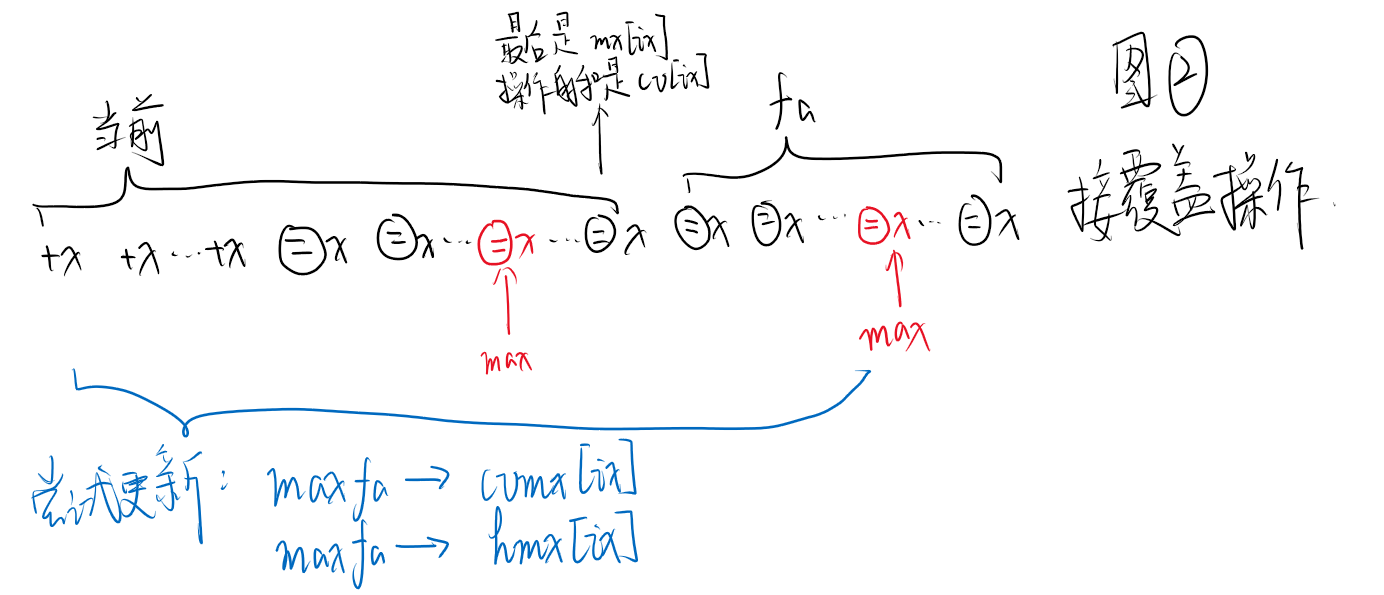
黑字同上;蓝字:maxfa->cvmx[ix],maxfa->hmx[ix]
maxfa 在代码中为 hc,表示父节点的覆盖操作的历史最大值
然后这样更新一下,就解决了关键性技术难题:lazytag与pushdown的定义与维护。
那接下来还用讲么不是有手就行。
板子:洛谷4314 CPU监控
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 100005
#define int long long
#define INF 0x3f3f3f3f
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,1,n) printf("%d ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,a[N];
void Input()
{
n=I();
F(i,1,n) a[i]=I();
}
class SegmentTree
{
public:
#define M N<<2
int mx[M],hmx[M]; // h: history
// 标记: +ad, 覆盖为 cv; 容易发现它可以合并
int ad[M],admx[M];
// ad: 所有加法标记的和 (加起来)
// admx: 加法标记达到的历史最大值 (相当于最大前缀和)
int cv[M],cvmx[M];
// cv: 所有覆盖标记的和 (取最后一个)
// cvmx: 覆盖标记达到的历史最大值
bool vis[M]; // 是否被覆盖了 (pushdown 清零)
#define ls ix<<1
#define rs ix<<1|1
#define lson ls,L,mid
#define rson rs,mid+1,R
void up(int ix)
{
mx[ix]=max(mx[ls],mx[rs]);
hmx[ix]=max(hmx[ls],hmx[rs]);
}
void addone(int ix,int a,int ha) // ha: 父亲的加法标记的历史最大值
{
if (vis[ix])
{
cvmx[ix]=max(cvmx[ix],cv[ix]+ha);
hmx[ix]=max(hmx[ix],mx[ix]+ha);
mx[ix]+=a; cv[ix]+=a; // 区间加合并到覆盖上
}
else
{
admx[ix]=max(admx[ix],ad[ix]+ha);
hmx[ix]=max(hmx[ix],mx[ix]+ha);
mx[ix]+=a; ad[ix]+=a;
}
}
void covone(int ix,int c,int hc) // hc: 父亲的覆盖标记的历史最大值
{
if (vis[ix])
{
cvmx[ix]=max(cvmx[ix],hc);
hmx[ix]=max(hmx[ix],hc);
mx[ix]=c; cv[ix]=c;
}
else
{
vis[ix]=1;
cvmx[ix]=hc;
hmx[ix]=max(hmx[ix],hc);
mx[ix]=c; cv[ix]=c;
}
}
void down(int ix)
{
// 这里不要判 ad[ix]!=0, 因为就算 =0, 中途也可能会很大, 而影响历史最大值
// 就好比你 +114514 -114514
addone(ls,ad[ix],admx[ix]);
addone(rs,ad[ix],admx[ix]);
ad[ix]=admx[ix]=0;
if (vis[ix])
{
covone(ls,cv[ix],cvmx[ix]);
covone(rs,cv[ix],cvmx[ix]);
vis[ix]=0;
cv[ix]=cvmx[ix]=0;
}
}
void build(int ix=1,int L=1,int R=n)
{
if (L==R)
{
mx[ix]=hmx[ix]=a[L];
return;
}
int mid=(L+R)>>1;
build(lson); build(rson); up(ix);
}
void add(int l,int r,int x,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
addone(ix,x,x);
return;
}
int mid=(L+R)>>1;
down(ix);
if (l<=mid) add(l,r,x,lson);
if (mid<r) add(l,r,x,rson);
up(ix);
}
void cov(int l,int r,int x,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
covone(ix,x,x);
return;
}
int mid=(L+R)>>1;
down(ix);
if (l<=mid) cov(l,r,x,lson);
if (mid<r) cov(l,r,x,rson);
up(ix);
}
int qmax(int l,int r,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
return mx[ix];
}
int mid=(L+R)>>1; int ans=-INF;
down(ix);
if (l<=mid) ans=max(ans,qmax(l,r,lson));
if (mid<r) ans=max(ans,qmax(l,r,rson));
return ans;
}
int qhmax(int l,int r,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
return hmx[ix];
}
int mid=(L+R)>>1; int ans=-INF;
down(ix);
if (l<=mid) ans=max(ans,qhmax(l,r,lson));
if (mid<r) ans=max(ans,qhmax(l,r,rson));
return ans;
}
}T;
void Sakuya()
{
T.build();
int m=I();
while(m-->0)
{
char s[4]; scanf("%s",s); char o=s[0];
if (o=='Q')
{
int l,r; Rd(l,r);
printf("%lld\n",T.qmax(l,r));
}
if (o=='A')
{
int l,r; Rd(l,r);
printf("%lld\n",T.qhmax(l,r));
}
if (o=='P')
{
int l,r,x; Rd(l,r,x);
T.add(l,r,x);
}
if (o=='C')
{
int l,r,x; Rd(l,r,x);
T.cov(l,r,x);
}
}
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}
吉司机带你飞 —— 论文题
要支持若干区间 (+a,对b取max) 的操作,然后问区间的max/历史max
我们发现 (+a,对b取max) 这个东西显然可以合并,\((a,b)+(c,d)=(a+c,\max(b+c,d))\)
考虑一开始有一个 \(x\)
做完第一个变成 \(\max(x+a,b)\)
做完第二个变成 \(\max(\max(x+a,b)+c,d)\)
\(=\max(\max(x+a+c,b+c),d)\) (把 \(c\) 放进 \(\max\) 里)
\(=\max(x+a+c,\max(b+c,d))\)
然后这个东西也可以取历史 \(\max\):若干数同时经历了 \((a,b),(c,d)\) 两操作,历史最大值的变化等价于操作 \((\max(a,b),\max(c,d))\)
证明引用(蒯)一张论文图

图线描述的是这个操作作用在 \(x\) 上,对应的 \(y\) 的图像:是一段平线加上一段45°的线。
两个图线的 \(\max\) (红色部分),就是历史 \(\max\) 的变化。为什么呢?
两个图线分别对应了两个时刻的操作的和。由于是历史 \(\max\),所以要对这两个时刻取个 \(\max\),就等价于两图线取 \(\max\)。而这红色的线,相当于平的取个max,斜的取个max,易得它就是 \((\max(a,b),\max(c,d))\) 。由此得到了历史 \(\max\) 的合并。
然后就像只有加法一样合并就行了。
代码:
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 500005
#define int long long
#define INF 1145141919810000ll
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,1,n) printf("%d ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,m,a[N];
void Input()
{
n=I(); m=I();
F(i,1,n) a[i]=I();
}
struct op{int a,b;}; // +a, 和b取max
// 注意空操作是 (0,-INF), 要初始化一下
op operator+(op x,op y) {return (op){max(x.a+y.a,-INF),max({x.b+y.a,y.b,-INF})};}
// 这里千万要和-INF取max,要不然会炸的只有20
op operator*(op x,op y) {return (op){max(x.a,y.a),max(x.b,y.b)};}
// 用乘法表示历史最大值的合并 (借鉴了以下博客的写法)
// https://www.cnblogs.com/AKMer/p/10241514.html
int calc(int x,op o) {return max(x+o.a,o.b);} // 把o操作在x上得到的值
class SegmentTree
{
public:
#define M N<<2
int mx[M],hmx[M]; // h: history
op tag[M],mxtag[M]; // 标记的和, 标记的历史最大
#define ls ix<<1
#define rs ix<<1|1
#define lson ls,L,mid
#define rson rs,mid+1,R
void up(int ix)
{
mx[ix]=max(mx[ls],mx[rs]);
hmx[ix]=max(hmx[ls],hmx[rs]);
}
void tagone(int ix,op t,op ht) // ht: 父亲节点的操作的历史最大值
{
hmx[ix]=max(hmx[ix],calc(mx[ix],ht));
mxtag[ix]=mxtag[ix]*(tag[ix]+ht);
mx[ix]=calc(mx[ix],t);
tag[ix]=tag[ix]+t;
}
void down(int ix)
{
tagone(ls,tag[ix],mxtag[ix]);
tagone(rs,tag[ix],mxtag[ix]);
tag[ix]=mxtag[ix]=(op){0,-INF};
}
void build(int ix=1,int L=1,int R=n)
{
tag[ix]=mxtag[ix]=(op){0,-INF};
if (L==R)
{
mx[ix]=hmx[ix]=a[L];
return;
}
int mid=(L+R)>>1;
build(lson); build(rson); up(ix);
}
void operate(int l,int r,op o,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
tagone(ix,o,o);
return;
}
int mid=(L+R)>>1;
down(ix);
if (l<=mid) operate(l,r,o,lson);
if (mid<r) operate(l,r,o,rson);
up(ix);
}
int qmax(int l,int r,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
return mx[ix];
}
int mid=(L+R)>>1;
down(ix); int ans=-INF;
if (l<=mid) ans=max(ans,qmax(l,r,lson));
if (mid<r) ans=max(ans,qmax(l,r,rson));
return ans;
}
int qhmax(int l,int r,int ix=1,int L=1,int R=n)
{
if (l<=L and R<=r)
{
return hmx[ix];
}
int mid=(L+R)>>1;
down(ix); int ans=-INF;
if (l<=mid) ans=max(ans,qhmax(l,r,lson));
if (mid<r) ans=max(ans,qhmax(l,r,rson));
return ans;
}
}T;
void Sakuya()
{
T.build();
while(m-->0)
{
int o=I();
if (o<=3)
{
int l,r,x; Rd(l,r,x);
op t;
if (o==1) t=(op){x,-INF};
if (o==2) t=(op){-x,0ll};
if (o==3) t=(op){-INF,x};
T.operate(l,r,t);
}
else if (o==4)
{
int p; Rd(p);
printf("%lld\n",T.qmax(p,p));
}
else if (o==5)
{
int p; Rd(p);
printf("%lld\n",T.qhmax(p,p));
}
}
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号