劳动节CF题总结
注:题意略
(vjudge上有中文翻译)
(可能会更新,因为我可能会再做点题)
感觉 CF 题对思维的训练意义很大,并且部分题对码力的训练也相当不错(WA自闭了)
CF1458E Nim Shortcuts
这就是那个WA自闭的题,最后都开始骗数据了
我们把状态 \((x,y)\) 看成平面直角坐标系上的点 \((x,y)\) 。那必输的点集相当于直线 \(y=x\) 上的点。我们记先手必输的点集为 \(S\)
考虑加入了某个“捷径” \((x_i,y_i)\),它会对 \(S\) 产生什么影响呢?
我们知道,有这样一个显然的结论
如果一个游戏状态的所有后继状态都是必胜状态,那么该状态为必输状态;
反之,只要有一个后继状态是必输状态,那么该状态为必胜状态
对于某个捷径 \((x_i,y_i)\),显然,它会让同一行、同一列的,x/y 坐标值比它大的所有点变成先手必胜。
显然,因为先手可以一步走到 \((x_i,y_i)\) 取胜
我们用 WPS 表格画出这个状态,红色格子表示先手必输,绿色格子表示先手必胜;红色格子里标 “S” 的表示它要么是 \((0,0)\) (最左上角),要么是一个捷径。
根据上面那个“显然的结论”,我们可以递推出整张图所有格子的胜负性
(我当时就是这么打草稿的)
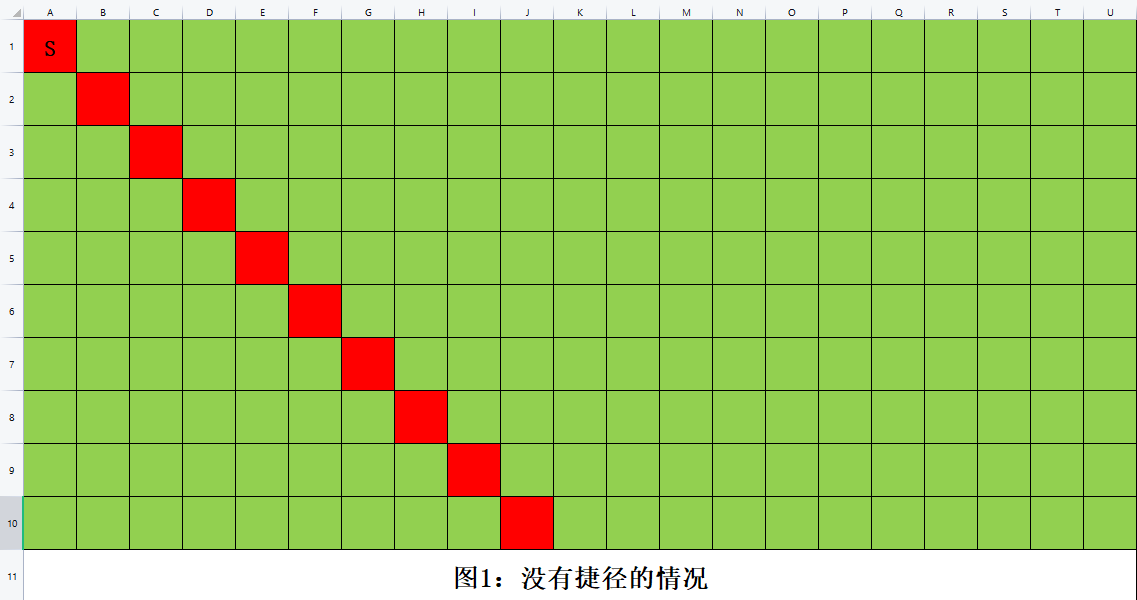
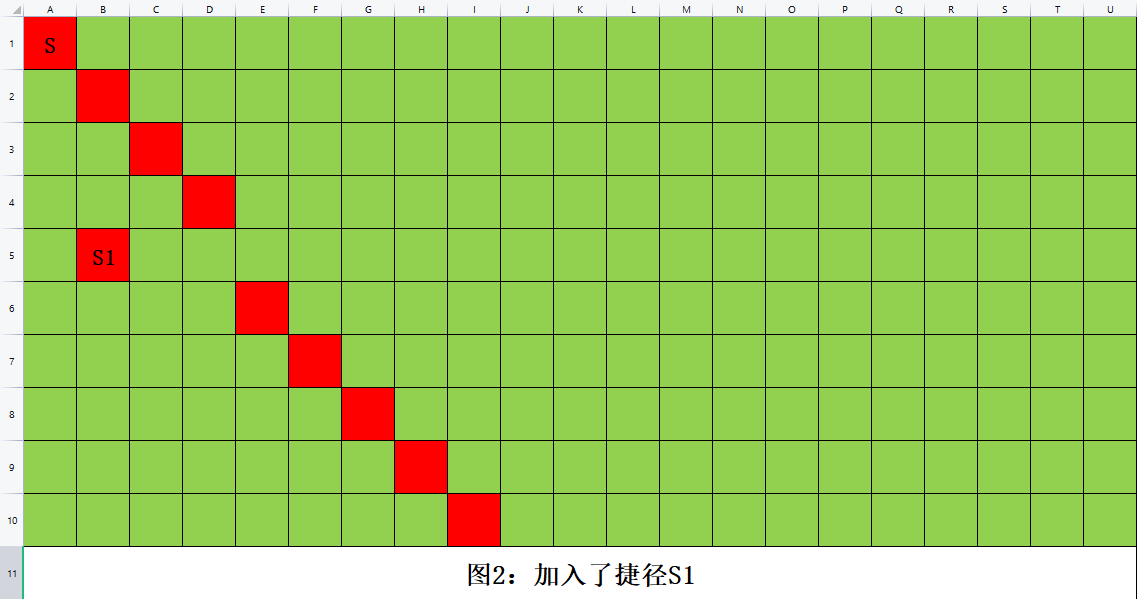
我们发现,加入一个新的捷径以后,由于它强行让它所在那一行、列的后面变成了绿色,原本一条红色的斜线的一部分被迫偏移了,向下偏了一格。体现在坐标系上,即 x/y 坐标被迫 +1。
如果您有兴致,可以多加几个捷径画一画(像我一样),然后就会发现,多几个捷径情况还是差不多的,只是这条线可能会偏移不止一格(因为捷径很多)。
那现在我们大概知道这个“必输线”怎么搞了:默认斜着走,如果同一行/列的前面有捷径就偏移;这样走得到的轨迹就是“必输线”,即集合 \(S\)。
这里我们判断它是否会“偏移”,要用
map记下每一行的捷径中最小的 \(x\) 坐标,和每一列的捷径中最小的 \(y\) 坐标,如果比当前点的 x/y 坐标来的小,就要偏移一下。
由于坐标范围是 \(1e9\) 的,所以每次要 lower_bound 找一下,看跳到哪里,而不能一个一个跳。
如何存储这个红色的“必输线”呢?我们发现,它是由若干个斜率为 \(1\) 的线段组成的,只是截距(\(y-x\))不同。而且它至多只会有 \(n\) 段,因为一个捷径最多让它多一段,所以总共最多也不会超过 \(n\) 段。
于是我们可以按截距分类。对于每一种截距,我们存 \(x\) 的取值范围。范围可能是多段区间并起来,所以我们要用一个 vector 来存。截距的范围很广,但是很少,还要再来一个 map。设 node 表示一个区间,那么我们使用的数据结构为:map<int,vector<node> >。由于总共不超过 \(n\) 段,所有 vector 的 size 的和也不会超过 \(n\)。这样预处理,时间复杂度 \(O(n\log n)\),空间复杂度 \(O(n)\)。
我是在刘汝佳的蓝书中见到这样的阴间结构的
此处为啥不离散化:会影响直线方程的计算
那对于每次询问 \((x,y)\),把 \(y-x\) 的截距拿出来,然后得到一个 vector<node ,判断一下 \(x\) 是否在里面即可,这个东西也很好二分解决。于是每次询问就是 \(\log\) 的。注意判一下初始位置就在捷径的情况。
一个细节:每次跳的时候,先处理“偏移”,再开始跳,因为你可能从 \((1,1)\) 就开始偏移。
另一个细节:
while循环处理偏移的时候,不要先搞 \(x\) 再搞 \(y\),详情见代码。一个注意:注意一下常数
代码:
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 100005
#define INF 0x3f3f3f3f
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,1,n) printf("%d ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,m;
struct node{int x,y;}; // node(x,y) 有多种含义, 有时代表一个点, 有时代表一个区间
bool operator<(node a,node b) {return a.x<b.x or (a.x==b.x and a.y<b.y);}
node s[N];
void Input()
{
Rd(n,m);
s[0]=(node){0,0};
F(i,1,n)
{
s[i]=(node){I(),I()};
if (s[i].x<=5 and s[i].y<=5)
{
printf("(%d,%d)\n",s[i].x,s[i].y);
}
}
}
map<int,vector<node> > range;
map<node,bool> have;
map<int,int> firx,firy;
// 先手败的点一定在若干条 y-x=k 的线段上
// range[k]: 对于所有 y-x=k 的线段, x 的取值范围
// 因为可能是若干个区间的并, 所以用 vector
int xp[N],yp[N]; // 记录下所有的x,y坐标(方便跳)
bool in_range(vector<node> &R,int p) // 判断 p 是否在 R 所代表的范围中
{
if (R.empty()) return false;
if (R[0].x>p) return false;
if (R.back().y<p) return false;
node las=*(upper_bound(all(R),(node){p,INF})-1);
// 最后一个左端点<=p的区间
if (las.y>=p) return true;
return false;
}
void Sakuya()
{
F(i,1,n) // 预处理: 每行第一个,每列第一个
{
xp[i]=s[i].x,yp[i]=s[i].y;
have[s[i]]=1;
if (firy.find(s[i].x)==firy.end())
{
firy[s[i].x]=s[i].y;
}
else
{
firy[s[i].x]=min(firy[s[i].x],s[i].y);
}
if (firx.find(s[i].y)==firx.end())
{
firx[s[i].y]=s[i].x;
}
else
{
firx[s[i].y]=min(firx[s[i].y],s[i].x);
}
}
xp[n+1]=INF; yp[n+1]=INF; // 哨兵
sort(xp+1,xp+n+1); sort(yp+1,yp+n+1);
node cur=(node){0,0}; // 从 (0,0) 开始
while(1) // 均摊 O(nlogn)
{
while(1)
{
bool flag=0;
if (firy.count(cur.x) and firy[cur.x]<=cur.y) ++cur.x,flag=1;
if (firx.count(cur.y) and firx[cur.y]<=cur.x) ++cur.y,flag=1;
if (!flag) break;
}
/*
注:
while(要偏x) ++cur.x;
while(要偏y) ++cur.y;
这样的写法是错误的, 因为处理完偏y之后, y坐标增加, 可能又有x要偏移了
比如这样的数据 (test#6 的一部分)
捷径: (1,0) (2,2) (3,0) (4,2) (5,2)
*/
int b=cur.y-cur.x;
if (!range.count(b))
{
range[b]=vector<node>();
} // 初始化一下, 防止阴间问题
int nx=*upper_bound(xp+1,xp+n+2,cur.x);
int ny=*upper_bound(yp+1,yp+n+2,cur.y);
if (nx>1e9 and ny>1e9) // 最后一段
{
range[b].p_b((node){cur.x,INF});
// 只要我们不停下来, x坐标就会不断延伸, 所以说, 不要停下来啊 (无端)
// 容易发现它确实是不断延伸的
break;
}
else
{
int d=min(nx-cur.x,ny-cur.y);
range[b].p_b((node){cur.x,cur.x+d-1});
cur.x+=d; cur.y+=d;
}
}
F(i,1,m)
{
int x=I(),y=I();
if (have[(node){x,y}] or (x==0 and y==0))
{
puts("LOSE");
continue;
}
int b=y-x;
if (in_range(range[b],x))
{
puts("LOSE");
}
else
{
puts("WIN");
}
}
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
freopen("in.txt","r",stdin);
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}
CF1500D Tiles for Bathroom
有一个显然的思路,肯定是钦定一个角,求出最长能扩展的边长 \(L\),然后对答案数组 \([1,L]\) 做区间 \(+1\)。
一开始我们可能会想到枚举左上角,然后像manacher一样继承一下右下角
但是我们发现它继承不起来,每次继承就要重新算一下出现次数的数组,并不能直接继承一部分。
(做到这我睡着了)
当你发现枚举一边不好用,那可以试试枚举另一边。(我醒来之后突然想到)考虑枚举右端点。注意到 \(q\) 很小,只要维护最近的 \(q\) 个 颜色 即可(换句话说要对相同颜色的去个重)。这样就可以把上面,左边,左上三个位置的颜色(一共 \(3q\) 个)合并一下得到当前离的“最近”的 \(q\) 个颜色。
直观上感觉很对,然而位置的坐标有两个数,取什么样的“最近”?
回到原问题,我们要用正方形来盖住这些颜色。所以,“距离”就是"至少需要多少边长的正方形才能覆盖“。由于 \(x,y\) 两个坐标都要覆盖到,所以是 \(x,y\) 坐标的差取 \(\max\)。那其实就是切比雪夫距离。
然后我们要求“最长扩展长度”,其实可以求"最短不合法长度“然后-1。”最短不合法长度“就是第 \(q+1\) 近的颜色的切比雪夫距离。
直接求第 \(q\) 近的颜色会有问题,就比如第 \(q\) 近的颜色切比雪夫距离为 \(k\),但是可能 \(q+1\) 近的颜色切比雪夫距离也是 \(k\)。此时如果覆盖一个边长为 \(k\) 的正方形,那就会覆盖到第 \(q+1\) 近的那个,从而导致存在多于 \(q\) 种颜色。
其实样例 \(2\) 就是一个反例,如果直接取第 \(q+1\) 近的,那你第四个数会输出 \(1\)
然后就随便做了。复杂度是 \(O(n^2q\log q)\),稍微卡下常。
代码
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 1502
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,1,n) printf("%d ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,q;
int a[N][N];
void Input()
{
Rd(n,q);
F(i,1,n) F(j,1,n)
{
a[i][j]=I();
}
}
struct node
{
int x,y,d; // d: 切比雪夫距离
};
bool cmp_d(node a,node b) {return a.d<b.d;}
vector<node> rec[N][N];
node t[35]; // 这个t用vector会TLE
int mxlen[N][N];
inline int cheb(int x1,int y1,int x2,int y2) {return max(abs(x1-x2),abs(y1-y2))+1;}
bool vis[N*N]; // 记下颜色, 每次用完要清理一下
int cf[N]; // 差分数组
void Sakuya()
{
FK(vis); FK(t);
F(i,1,n) F(j,1,n)
{
node cur=(node){i,j,1};
int tpos=0;
t[++tpos]=cur;
if (j>1) for(auto x:rec[i][j-1]) t[++tpos]=((node){x.x,x.y,cheb(x.x,x.y,i,j)});
if (i>1) for(auto x:rec[i-1][j]) t[++tpos]=((node){x.x,x.y,cheb(x.x,x.y,i,j)});
if (i>1 and j>1) for(auto x:rec[i-1][j-1]) t[++tpos]=((node){x.x,x.y,cheb(x.x,x.y,i,j)});
sort(t+1,t+tpos+1,cmp_d);
int tot=0;
mxlen[i][j]=114514;
// 注:如果颜色一共都没有 q+1 个,那么说明随便取都可以,此时的答案是 min(i,j)
// 为了合并两种情况省去一些讨论, 我们令 mxlen 的初始值为 INF,然后最后和 min(i,j) 取 min
// (这个INF臭死力)
rec[i][j].clear();
F(ii,1,tpos)
{
node x=t[ii];
int c=a[x.x][x.y];
if (!vis[c]) // 对颜色去重
{
vis[c]=1;
rec[i][j].p_b(x);
++tot;
if (tot==q+1) // 取到第 q+1 个
{
mxlen[i][j]=x.d-1;
break;
}
}
}
mxlen[i][j]=min({mxlen[i][j],i,j});
F(ii,1,tpos)
{
node x=t[ii];
vis[a[x.x][x.y]]=0;
}
}
F(i,1,n) F(j,1,n)
{
++cf[0]; --cf[mxlen[i][j]+1];
}
F(i,1,n) cf[i]+=cf[i-1];
F(i,1,n) printf("%d\n",cf[i]);
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号