ZJOI2018]历史 做题心得
[ZJOI2018]历史 做题心得
whk了好久,来点lct练练手,免得手生了
是一个思维好题,巧妙运用了 LCT 的 access
做法概要
dp一遍求出初始的答案
用 LCT 维护修改
不考虑修改,求初始答案
考虑每条边的贡献加起来。
发现边的选择并没有后效性,只需要分别保证每条边改的次数最多加起来就行了。
所以可以像树形 dp 一样解决不带修改的问题。
为什么没有后效性:
设 \(f=fa[u],f_2=fa[f]\),现在选到了 \((u,f)\) 这条边。
对于 \(u\) 子树 中的每个点 \(v\),\(v\) 城市的崛起,除非是第一次,都会让 \((u,f)\) 边的势力改变,并可能对答案产生贡献。
(如果这次崛起的城市和上次崛起的城市,位于 \(u\) 的同一颗子树内,那么就会在 \(u\) 下面贡献,不会到 \((u,f)\) 这边贡献 )
注意到灾难度算的是 不同 的势力数量。每次有新城市崛起的时候,在 \((u,f)\) 边已经算过了一次贡献,那么在 \((f,f_2)\) 边就没有贡献了。
所以说 \(u\) 子树中的选择只会对 \(u,f\) 产生影响,一定不会影响 \((f,f_2)\)
那么考虑一下 \((u,f)\) 这条边要被搞多少次。
上面已经提到,必须是在 \(u\) 的 不同 子树里选,或者直接选择 \(u\) 本身,才会产生贡献。
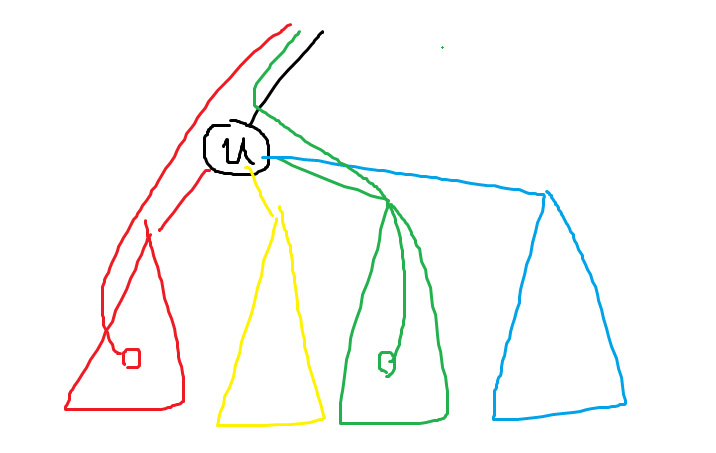
↑ 如图,必须在不同的子树里两个城市先后崛起 (如图中的红色点和绿色点),才会让 \((u,f)\) 边贡献。
相反,如果在同一颗子树里,比如说两个红色子树的城市,先后崛起
那么它的贡献就会贡献到 \(u\) 下面的红色边,而不是 \((u,f)\) 边
考虑计算最大能贡献多少次。设 \(s[u]\) 表示 \(u\) 子树中 \(a\) 的和。 ( \(a\) 就是崛起多少次那个 \(a\))
设 \(u\) 有 \(m\) 个儿子,为 \(v_1,v_2...v_m\)。
那相当于有 \(m+1\) 种颜色的球,每种颜色的球分别有:\(a[u],s[v_1],s[v_2]...s[v_m]\) 个
问题转化成,把这些球排成一排,最大化相邻的球颜色不同的对数。设 \(S\) 为总个数,\(M\) 为最大的个数,并且这个数量最大的颜色是 \(c_M\)。
即 \(S=a[u]+s[v_1]+s[v_2]...+s[v_m]\),\(M=\max(a[u],s[v_1],s[v_2]...s[v_m])\),\(c_M\) 表示 \(M\) 取的是哪一项
如果 \(M>S-M\),那么最优方案显然就是,每次先放除了 \(c_M\) 的一个颜色,然后放一个 \(c_M\)。这样能做到不同的数量是 \(2*(S-M)\)。
否则,可以一个一个轮流的放,做到相邻的都不同。答案是 \(S-1\)。
然后就可以求出初始的答案了。
分析性质,维护修改
\(M>S-M\) ,即 \(2M>S\)。
考虑一个 \(u\),它 \(s\) 最大的儿子是 \(v_k\)。
定义:如果 \(2*s[v_k]>s[u]\),那么称 \(v_k\) 是 \(u\) 的 重儿子。类似的,\((u,v_k)\) 为 重边,重边组成的链是 重链。除了重边之外的边称为 轻边。
轻边的数量是多少呢?轻边满足:\(2*s[v]\le s[u]\),那每走一条轻边,\(s\) 至少要 \(*2\),那这个复杂度就是 \(\log\) 级别的。
注意这里的 \(\le\) 。代码实现中也要注意。
如果您 WA 50,错的是后半部分,那可能就是这个问题
显然,一个 \(u\) 的重儿子一定不超过一个(注意,可能没有)
考虑一次修改,对重链的影响:答案是 \(2*(S-M)\), \(S,M\) 的增加量都一样,消掉了,于是 \(S-M\) 是没有变化的。
换句话说,修改操作对于一条重链的答案没有任何影响。那它就只对轻边有影响。
于是得到,贡献答案只需要考虑轻边
那直接树链剖分跳就完了?那不太行,发现每次修改可能会改变一些重边的连接。
但是假设改的是 \(u\),那么 \(u\) 到根的链只可能变重,不可能变轻 (因为是增加)。
于是得到,修改链接只需要考虑轻边
它可能会翻身成为重边, 也可能会让原来的重边变轻
综上,我们 只需要考虑轻边
注意到要改变连接,用 \(LCT\) 维护。由于只需要考虑轻边,于是只需要它一个 \(access\) ,中途顺带着改一改,就解决了。
代码
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 400005
#define int long long
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,1,n) printf("%d ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,m,a[N];
class Graph
{
public:
struct edge{int v,nx;} e[N<<1];
int head[N]; int ecnt=-1;
void clear()
{
ecnt=-1; MEM(head,-1); MEM(e,-1);
}
void add(int u,int v)
{
e[++ecnt]=(edge){v,head[u]}; head[u]=ecnt;
} void add2(int u,int v) {add(u,v); add(v,u);}
int st(int u) {return head[u];}
int to(int i) {return e[i].v;}
int nx(int i) {return e[i].nx;}
}G;
void Input()
{
Rd(n,m); F(i,1,n) a[i]=I();
G.clear();
F(i,1,n-1)
{
int u,v; Rd(u,v);
G.add2(u,v);
}
}
// 定义重儿子: size[v]*2>size[u] 的 v 是 u 的重儿子
// LCT 维护重链
int ans=0;
class Link_Cut_Tree
{
public:
int fa[N],ch[N][2];
int val[N],other[N],s[N]; // other: 轻子树的和
int res[N];
#define ls(u) ch[u][0]
#define rs(u) ch[u][1]
#define sub(u) (s[u]-s[ls(u)])
// LCT 的辅助树上, 左子树表示祖先部分
// 所以减去祖先的部分就是实际的子树
bool id(int u) {return u==rs(fa[u]);}
bool rt(int u) {return u!=ls(fa[u]) and u!=rs(fa[u]);}
void up(int u)
{
s[u]=s[ls(u)]+s[rs(u)]+val[u]+other[u];
}
void upans(int u)
{
ans-=res[u];
res[u]=sub(u)-1;
if (rs(u)) res[u]=(sub(u)-s[rs(u)])*2;
if (val[u]*2>sub(u)) res[u]=(sub(u)-val[u])*2;
ans+=res[u];
}
void rot(int u)
{
int f=fa[u],f2=fa[f],i=id(u),i2=id(f),w=ch[u][i^1];
if (!rt(f)) ch[f2][i2]=u; ch[u][i^1]=f; ch[f][i]=w;
if (w) fa[w]=f; fa[f]=u; fa[u]=f2;
up(f); up(u);
}
void sp(int u)
{
while(!rt(u))
{
int f=fa[u];
if (!rt(f)) rot(id(u)==id(f)?f:u);
rot(u);
}
}
void ac(int u,int a)
{
for(int p=0;u;p=u,u=fa[u])
{
sp(u); s[u]+=a; u[p?other:val]+=a;
if (s[rs(u)]*2<=sub(u)) // 原来的重儿子不再重
{
other[u]+=s[rs(u)]; rs(u)=0;
}
if (s[p]*2>sub(u)) // 更新的儿子变重
{
other[u]-=s[p]; rs(u)=p;
}
upans(u);
}
}
}T;
void DFS(int u,int f)
{
T.val[u]=T.s[u]=a[u];
T.fa[u]=f;
Tra(i,u) if (v!=f)
{
DFS(v,u);
T.s[u]+=T.s[v];
}
int k=0;
Tra(i,u) if (v!=f)
{
if (T.s[v]*2>T.s[u]) k=v;
}
T.ch[u][1]=k; // 重儿子
T.other[u]=T.s[u]-a[u]-T.s[k];
T.upans(u);
}
void Sakuya()
{
DFS(1,0);
printf("%lld\n",ans);
F(i,1,m)
{
int x,y; Rd(x,y);
T.ac(x,y);
printf("%lld\n",ans);
}
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号