tricks - 思维
tricks
系列
随机的性质
bitmask
建图
基本
黑白染色
主体思想:二维平面,每次只能走一步,一般可以考虑黑白染色,也许可以考虑和二分图套在一起
一般可以帮助决策,比如说做贪心题,或者博弈。
并查集维护值域
主体思想:对于维护一个区间中形如“把所有值=x的变成y” 的操作,把相同值的并到一块,然后合并值=x和值=y的即可。
此技巧常用于分块中,对于每一块维护这样一个并查集。如 [Ynoi2018]五彩斑斓的世界。
那个题我被卡常了qaq,代码略
带根号的数三元环
主体思想:通过某些技巧使复杂度为 \(O(m\sqrt{m})\)
详解见题解。
根号分治
主体思想:小于根号和大于根号的情况分开讨论,平衡总复杂度
另:根据点的度数,小于根号和大于根号的分开讨论。(数三元环也用到了这个trick)
当 \(k>\sqrt{n}\) 的时候暴力跳,当 \(k<\sqrt{n}\) 的时候预处理。
调和级数哈希
主体思想:枚举长度 \(k\),每次用哈希检测答案,复杂度 \(O(\sum \lfloor \dfrac{n}{k}\rfloor * H)\),\(H\) 为哈希复杂度(一般是 \(O(1)\),可能会有 \(log\))
例题1中,评论区神仙 @Tweetuzki 已经讲完了做法;
例题2中,枚举 \(k\) ,然后 \(O(n/k)\) 的跑一遍即可。然而这题还有一个问题,对于一个字符串,我们把它和它的反串视作本质相同的串,这咋哈希?
留到下一个trick里讲。
多属性哈希
主体思想:如果一个元素有若干种属性值,对于属性值一样的元素视作“本质相同的元素”,并且属性值很少;那我们可以把属性值的哈希值排一下序,然后序列哈希。
对于每个串,我们可以认为它有两个“属性值”:原串的哈希值,和反串的哈希值
我们把这两个值排一下序然后哈希即可...
两个数的哈希可以直接做:\((a,b) \rightarrow (a\times base+b)\bmod M\)
时光倒流
主体思想:一个序列, 或者一堆操作, 正着考虑不好整,就 假装自己是小青蛙 时光倒流,反过来考虑。
例1 经典题 [AHOI2005] 航线规划:树,删边,求点距离
逆向,删边变加边,随便做:树剖/LCT
例2 CF1366E Two Arrays:要求把序列 \(a\) 划分成 \(k\) 段,每一段的最小值递增,并且拼起来恰好是一个长度为 \(k\) 的另一个序列 \(b\)。给定 \(a,b\) ,求合法划分的方案数
最小值递增,那在段与段之间,每个段的最小值也是后缀最小值。那我们从后往前考虑,假设后缀最小值第一个等于 \(b_i\) 的位置是 \(p\),并且后缀最小值等于 \(b_i\) 的一共有 \(k\) 个。显然它们会在同一个区间里。那么从这这一段区间里任选一个位置,划到 \(p\),作为第 \(i\) 段,就可以满足条件。并且没有其他位置能满足条件。
所以答案就是,求出后缀最小值,求出数量数组cnt,\(\prod cnt_{b_i}\)
Kruskal重构树
主体思想:每次合并两个点的时候,新建一个虚点作为两个节点的父节点。
容易发现,上一次成功合并之后得到的点 \(P\),一定是森林的若干个根之一。
并且这个结构很方便实现撤销:我们把上次的点 \(P\) 标记为删除;点 \(u\) 所在的联通块,就先找到它祖先中,深度最小的没被删除的点 \(F\),然后 \(F\) 的子树中的叶子节点就是 \(u\) 所在的联通块。
例题留到下一个 trick 里面一块讲。
时光反复横跳
主体思想:“时光倒流”那个trick告诉我们可以反过来考虑,而如果有些必须正着完成的事情,先反过来一遍,用撤销的方法做回去。
例题:CF1416D
先反过来,得到最后删完的图;然后Kruskal重构树连回去,然后不断的撤销就可以了。每次找最大那个就用线段树瞎jb维护一下就行了。
主席树维护二分
主体思想:二分每次检测 \(mid\) 的时候序列都不一样,相邻的两个 \(mid\) 改变的并不多,用主席树全部存下来,再维护点啥,每次可以 \(O(log)\) 的检测。
这题暴力二分做法:
对于 \(mid\),大于等于它的视为 \(1\),其它的视为 \(-1\),然后求 \([a,b]\) 区间的最大后缀和,\((b,c)\) 区间的和,\([c,d]\) 区间的最大前缀和,加起来即可。
我们发现这三个都能线段树维护。并且,对于 \(mid\rightarrow mid+1\),只有原来 \(=mid\) 的地方从 \(1\) 变成了 \(-1\)。用 \(vector\) 记录下这些位置,每次修改,总修改次数是 \(n\) 次。直接主席树维护即可。
带上主席树复杂度就是 \(n\log n\),即可求出 \(mid=[1,n]\) 时所有的检测用的数组。然后线段树区间和就可以 \(\log\) 的求,也就是 \(O(\log n)\) 检测一个 \(mid\),套上二分复杂度就是 \(O(\log^2 n)\) 回答每个询问。
(这玩意还是个黑题,太水了吧
基环树上dp
主体思想:在环上随便钦定两个相邻的点,以两点为根跑树形 \(dp\)
这个做法有一些条件的...这题中,任意断一条边都对,才能这么做
如果断不同的边答案不一样,那就要枚举了,时间复杂度爆炸(有的题里可能不会
回到这题。这题里如果是一颗正常的树,显然是最大独立集问题。
然后我们随便钦定一个环上的 \(u,v\),求 \(max(dp[u][0],dp[v][0])\),即可
换根dp
主体思想:先求出以 \(u\) 为根的答案,然后再 \(dfs\) 一遍继承父亲的答案。
先存储每个点往下的带权距离和。
去掉这个点对父亲的贡献,第二遍 \(dfs\) 的时候从父亲更新到儿子,以求出以每个点为根的带权距离和。
相对顺序不变
主体思想:变化是规律的,如果能证出来顺序不变,那直接二分即可
例:第 \(i\) 个数每次都加 \(a_i\),初始为 \(0\)。显然这个顺序不变。每次要求某时刻多少个 \(>k\) 的,直接二分
线段树节点合并时二分
主体思想:左儿子和右儿子合并的时候,只有右儿子的一段前缀会没有,二分即可
势能分析线段树
主体思想:线段树+优化暴力,用神奇的性质保证复杂度为 \(O(nlogn*K)\)
例题1:区间开根下取整,值域在 \([0,10^{12}]\)
每个数被开 \(6\) 次就变成 \(0/1\),而 \(0/1\) 开根取整还是自己,于是不用管了;
于是这题复杂度是 \(O(K*nlogn)\),其中 \(K_{max}=6\)
每个数只会在负变正的时候需要暴力讨论,其它时候绝对值都是-/+
于是 \(K_{max}=2\),然后这题就是个sb题,代码略(其实是没写,百度抄一个
gcd 变 phi
主体思想:\((a,b)=\sum\limits_{d|a,d|b} \phi(d)\)
set 维护精确枚举
主体思想:用 set 存储合法的扩展,保证复杂度
PS:例题中,把 \(set\) 部分的代码换成
F(i,1,n) if (!vis[i])
时间复杂度就变成了 \(O(n^2)\)
因数id
注:后设 \(D=\max \sigma_0(n)\)。它用来估算复杂度。
主体思想:当一个问题只涉及某个数 \(n\) 的因数时,我们可以把它的因数,从 \(1\) 开始重新编号,把规模转化为 \(\sigma_0(n)\)。注意,由于 \(D\) 很小,我们经常会需要处理一个大小为 \(D^2\) 的二维数组。
这在 \(n\le 10^9\) 时同样适用,因为此时 \(D=1344\)。
例1: arc004-4,问 \(n\) 能用多少种方法拆成 \(m\) 个整数的乘积。\(n\le 10^9,m\le 10^5\)
首先用组合方法求出安排符号的方案。然后注意到 \(>1\) 的数不会超过 \(\log n\) 个,然后剩下都是 \(1\)。用组合数方法求出安排 \(1\) 位置的方案。现在只需要求用 \(\le 30\) 个数拼出来 \(n\) 的方案数。
用上面那个 trick 求出每个因数的编号,设记下来第 \(i\) 个因数为 \(num[i]\),因数 \(d\) 的编号为 \(id[d]\)。
设 \(dp[i][j]\) 表示选了 \(i\) 个因数拼出来 \(id=j\) 的方案数。枚举选多少个,枚举一个 \(id\) 为 \(x\),枚举一个 \(id\) 为 \(y\),用 dp[i-1][id[num[x]/num[y]]] 来更新 dp[i][x]。注意一个前提是 num[x] 是 num[y] 的倍数。
可我们并不能记下 \(id\),每次求 \(id\) 还需要一次二分。这样直接转移带两个 \(\log\)(枚举选多少个是一个 \(\log\),还有一个二分的 \(\log\))。
考虑把二分的那一步预处理出来,设 rec_div[i][j] 表示 id(num[x]/num[y])。这样就省下一个 log,变为了可以通过的一个 \(\log\)。
例2: noi.ac329 你要在一个 \(n\times m\) 的棋盘里,第一行选一个,中间行选一个或两个,最后一行选一个,使得乘积是 \(A\) 的倍数。输出方案数 \(\% H\) 。\(n\le 200,m\le 10^4,A\le 2\times 10^5, H\le 3\times 10^4\)
首先每个位置和 \(A\) 先取个 \(\gcd\),这很显然。不是公因数的部分,去掉了也没有任何影响。
然后把 \(A\) 做一遍上面那个 trick,同样得到 \(id\) 与 \(num\)。不同的是这次 \(id\) 直接可以开下来数组。
接下来就 \(dp[i][j]\) 表示选到前 \(i\) 行乘积的 \(id=j\) 方案数。然而中间的行可以选两个数,而我们不能 \(O(m^2)\) 枚举,咋整?事实上我们可以先 \(O(m)\) 的枚举,记一个 \(cnt[i]\) 表示这一行中 \(id=i\) 的数个数。然后在 \(cnt\) 上 \(O(D^2)\) 转移。由于 \(D\) 很小,便省下了很多时间。
这里再注意一个细节,\(O(D^2)\) 转移的时候涉及到乘法,乘法完了还要再取一个 \(\gcd\) ,又会凭空多 \(\log\)。类似上面,设 \(mul[i][j]\) 表示 \(num[i]\times num[j]\) 和 \(A\) 取 \(\gcd\) ,省下每次做的 \(\log\)。
复杂度便是 \(O(nD^2+nm)\)
幂的意义
主体思想:把某个数的 \(k\) 次方,看成是选了 \(k\) 次一样的方案数。
例题:NOI2009管道取珠(经典,略)
树上信息记父亲头上
主体思想:如题,我们把一个点 \(u\) 的信息记在 \(fa_u\) 上。
naive例题:树上多次询问,带修改,求一个点的所有儿子的权值和。
设 \(s(i)\) 表示 \(i\) 的儿子和,每次改一个点 \(u\),就修改 \(s(fa(u))\)。
不naive例题:树上多次询问,带修改,求一条路径的“毛毛虫”和。对于路径 \(u,v\),毛毛虫和定义为:\(\sum\limits_{x} a_x [\exist x',x'\in path(u,v)][x\not\in path(u,v)]\)。
后面那一串,说人话就是,\(x\) 不在路径上而 \(x\) 存在一条出边到路径上。把图画出来,它长的很像一个毛毛虫。
沿用上一题的 \(s\)。我们发现这玩意就是路径的 \(s\) 的和减去路径的 \(a\) 的和,加上LCA的单点值。用树剖维护这个路径和即可。
非口胡题:noi.ac2402
给定树上的若干条链,链带权;选择若干条链,不相交(没公共点),最大化选出来链的权值和。
点数,链数,权值都是1e5。
我们设 \(f(i)\) 表示 \(i\) 的子树里面选链的最大权值和。枚举一条以 \(i\) 为 LCA 的链,考虑下面怎么选,发现就是上一题里面,把 \(f\) 当成权值之后的 “毛毛虫” 和。树剖维护即可。
神秘
另类回文
主体思想:把平常写的 == 换成其它的匹配函数
在这题中,匹配函数为:
然后要你求有多少回文子串。
当然,这个 \(f\) 也可以是任意神奇的函数
↑ 这句话是假的,\(f\) 必须要满足一些性质:
对于任意两个长度相同的串 \(a,b\),对于所有 \(1\le i\le |a|\),满足 \(f(a_i,b_i)=1\),则有:\(a,b\) 两串回文等价。
两个串回文等价定义为,“是否回文”这个bool值相同。
这个题中,如果 \(f(a_i,b_i)=1\),那么 \(a\) 和 \(b\) 恰好是二进制取反的关系,注意到 \(f\) 比较函数中两字符同时取反不会影响 \(f\) 的值,所以 \(a,b\) 显然是回文等价的。
然后我们把这个函数处理出来跑 Manacher 就可以了。它可以求出以任意点为中心的最长回文半径。这样就可以求出最长的回文子串长度,以及回文子串的种类数。
换方向求和 (Abel变换)
主体思想:注意到正整数 \(x=\sum\limits_{i}[i\le x]\),用这个式子把原来的和写成另一个形式。
可以用这个图来描述:
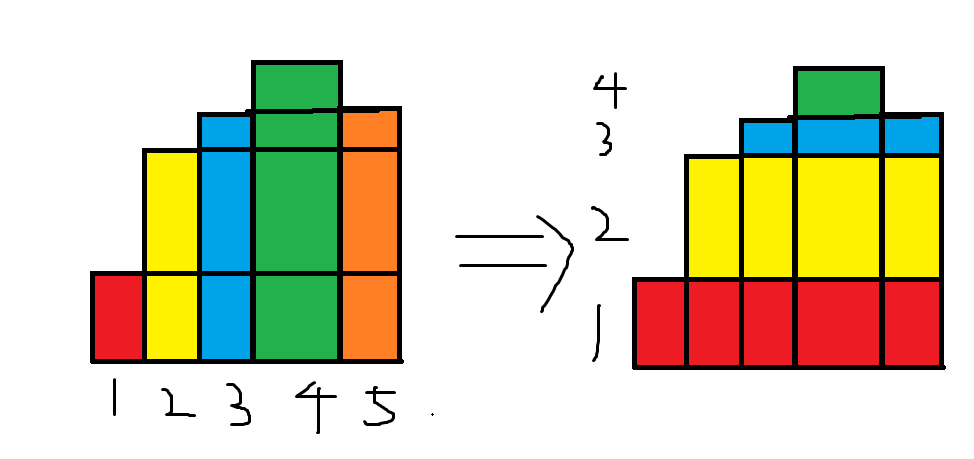
它可以推导出经典结论:\(x\) 为随机正整数,\(E(x)=\sum\limits P(x\ge i)\)。
例题1: 集合
设 \(k\) 的答案为 \(f_k\)
一方面,直接钦点最小值,答案是
\[f_k=\sum\limits_{i=1}^{n} T^i \times \binom{n-i}{k-1} \]另一方面,分段枚举最小值,并累计差量 (即这个trick),答案也是
\[T\times \binom{n}{k} + \sum\limits_{i=1}^{n-1} (T^{i+1}-T^i)\times \binom{n-i}{k} \](先特判 \(\ge 1\) 的情况,后面枚举的 \(i\) 表示最小值 \(>i\))
后面的式子提一个 \(T^i\) 出来,发现它就是 \(f_{k+1}\)(注意到这里的 \(\sum\) 可以取到 \(n\),这时候后面的组合数为 \(0\),不影响)
于是有 \(f_k=T\binom{n}{k}+(T-1)f_{k+1}\)
显然有 \(f_n=T\) 。不断用这个式子,从 \(k\) 变到 \(n\),手推几个即可发现:
\[f_k=\sum\limits_{i=0}^{n-k} T(T-1)^i\times \binom{n}{k+i} \]再来点变换:\((T-1)^i=\dfrac{(T-1)^{k+i}}{(T-1)^k}\) (显然),然后把常数 \((T-1)^k\) 和 \(T\) 提到 \(\sum\) 的外面
变成:
\[f_k=\dfrac{T}{(T-1)^k} \sum\limits_{i=0}^{n-k} (T-1)^{i+k}\times \binom{n}{i+k}\\ =\dfrac{T}{(T-1)^k} \sum\limits_{i=k}^{n} (T-1)^{i}\times \binom{n}{i}\\ \]我们注意到后面的式子,和二项式定理的式子,只差了 \(k\) 项。而 \(k\) 很小,只有 \(1e7\),于是预处理阶乘,逆元,阶乘逆元等,暴力算出这 \(k\) 项,用二项式定理化成的 \(A^n\) 减去这 \(k\) 项的和,就可以得到后面的,再加上前面的即可求出和,然后除一个 \(\binom{n}{k}\) 得期望。
例题2:见 这篇
数论域的 log
主体思想:\(\log(ab)=\log(a)+\log(b)\),质因子个数函数 \(\omega\) 和它有相同的性质。
幂分类讨论
主体思想: 答案与指数函数有关,并且要最小化。这时,当幂小的时候暴力做,幂大的时候,优先让指数小,再让别的小,转化成双关键字的最小化问题。
和根号分治的思想有几分类似,大数据和小数据两种方法做。
例:CF1442C Graph Transpositions:一张有向图上要从 \(1\) 走到 \(n\),走边花费都是 \(1\)。每次走一条边都可以选择是否对 所有的边 做一次反向操作。如果一共做 \(t\) 个反向操作,花费为 \(2^t-1\)。输出最小的从 \(1\) 走到 \(n\) 的总花费,模 \(998244353\)。先最小,再取模。\(n\le 2e5\)
假设 \(t\ge 20\),那么每增加一个 \(t\) 的花费就是 \(1e6\) 级别的,这比在图上随便走都来的大。对于这种情况,把有向边 \((u,v)\) 看成是:\(u\rightarrow v,w=(0,1)\) ;\(v\rightarrow u,w=(1,1)\)。然后跑一个双关键字最短路,假设最短边权和为 \((a,b)\) ,实际答案为 \((2^a-1)+b\)。
细节:这里要分一下奇偶讨论,因为翻转了奇数次和偶数次的时候,边的正反就会不一样,然后边权的第一关键字就要相应的有变化。
双关键字最短路就是每条边的权是一个二元组,然后要先让第一关键字的和最小,在此基础上再让第二关键字的和最小
做法非常simple,就是dijkstra的时候记在priority_queue里的东西从int变成pair<int,int>就行了。如果想方便可以再重载一个+运算符,然后就和普通最短路几乎一模一样了
假设 \(t\le 20\),设 \(d(i,k)\) 表示走到 \(i\) ,翻转了 \(k\) 次的最短路。这个可以暴力做,复杂度是 \(O(20n \times \log 20n)\) (本质是一个分层图)。
总的复杂度就是 \(O(20n\log n)\) 了。\(2e5\),随便过。
biteset 维护 mutiset
主体思想:众所周知bitset可以维护一个集合(用第 \(i\) 位是 0/1 表示第 \(i\) 个元素有无),然后多重集合就令每个元素占有一块连续的区间,从 \(p_i\) 开始,然后第 \(i\) 个元素的第 \(x\) 次出现就看 \(p_i+x-1\) 是否为 \(1\)。
多重集合取一下and,会把每种元素的个数 取min。取一下 or 就是个数 取max。
莫队+三个bitset
细节:由于要同时维护三个,我们不得不记下所有中途的bitset,然而空间不允许;如果 \(m\le 10^4\),才能开的下,而 \(m\le 10^5\)。那可以令 \(T=10^4\),然后每 \(T\) 次当做一组数据,当成是多组数据来跑,用时间换空间,即可。
等根变换
主体思想:两个式子的根集合一样,那么我们认为两个式子差常数倍;如果某一次项的数值一样(比如最高次,或者常数项,常用的),那可以认为两式子一样
经典结论:\(p\) 为质数,\(\prod\limits_{i=0}^{p-1} (x+i)\equiv (x^{p-1}-1)x\pmod{p}\)
考虑费马小定理,右式的根显然是 \([0,p-1]\),左边也是,而且最高次项都是 \(1\),所以两式相同。
来自马老师的指导:
这玩意显然两边都是 \(0\) 。所以式子成立。
拆排序的贡献
主体思想:把顺序和拆成贡献的形式
注意到,对于正整数 \(x\),它等于 \(\sum\limits_{i=1}^{\infin} [i\le x]\)
然后比如说我们可以枚举一个数 \(i\),看看有多少个 \(\ge i\) 的,就贡献一波
该技巧尤其常用于期望相关题目,结合期望线性性拆开。当然,在数位dp中也被用到一次,见 这篇


 浙公网安备 33010602011771号
浙公网安备 33010602011771号