左程云算法课笔记

左程云算法课笔记

本文主要是笔者在研一寒假时的听课笔记，听课链接一周刷爆LeetCode，算法大神左神（左程云）耗时100天打造算法与数据结构

当然这个也有一些问题，比如难度对于新手略大，我现在在刷力扣一遍复习，也把这个作为一个笔记的存储吧，有些这里的记录比较方便，例如排序之类的。

p39:

二叉树调整错误节点

一棵二叉树原本是搜索二叉树，但是其中有两个节点调换了位置，使得这棵二叉树不再是搜索二叉树，请找到这两个错误节点并返回。已知二叉树中所有节点的值都不一样，给定二叉树的头节点 head，返回一个长度为2的二叉树节点类型的数组errs，errs[0]表示一个错误节点， errs[1]表示另一个错误节点。

进阶: 如果在原问题中得到了这两个错误节点，我们当然可以通过交换两个节点的节点值的方式让整棵二叉树重新成为搜索二叉树。但现在要求你不能这么做，而是在结构上完全交换两个节点的位置，请实现调整的函数。

思路：找到这两个节点很简单，就是中序遍历中的e1和e2，e1是第一次降序中的第一个节点，e2是最后一次降序的最后一个节点，那么与此同时需要调整这俩的结构，如果调整完发现还是有降序说明不止两个节点错了，这两个节点的各种方式有16种，又因为中序遍历e1在e2的前面，因此可以省去两种，一种14种情况。。。

package class06;

import java.util.Stack;

public class Problem02_RecoverBST {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static Node[] getTwoErrNodes(Node head) {
		Node[] errs = new Node[2];
		if (head == null) {
			return errs;
		}
		Stack<Node> stack = new Stack<Node>();
		Node pre = null;
		while (!stack.isEmpty() || head != null) {
			if (head != null) {
				stack.push(head);
				head = head.left;
			} else {
				head = stack.pop();
				if (pre != null && pre.value > head.value) {
					errs[0] = errs[0] == null ? pre : errs[0];
					errs[1] = head;
				}
				pre = head;
				head = head.right;
			}
		}
		return errs;
	}

	public static Node[] getTwoErrParents(Node head, Node e1, Node e2) {
		Node[] parents = new Node[2];
		if (head == null) {
			return parents;
		}
		Stack<Node> stack = new Stack<Node>();
		while (!stack.isEmpty() || head != null) {
			if (head != null) {
				stack.push(head);
				head = head.left;
			} else {
				head = stack.pop();
				if (head.left == e1 || head.right == e1) {
					parents[0] = head;
				}
				if (head.left == e2 || head.right == e2) {
					parents[1] = head;
				}
				head = head.right;
			}
		}
		return parents;
	}

	public static Node recoverTree(Node head) {
		Node[] errs = getTwoErrNodes(head);
		Node[] parents = getTwoErrParents(head, errs[0], errs[1]);
		Node e1 = errs[0];
		Node e1P = parents[0];
		Node e1L = e1.left;
		Node e1R = e1.right;
		Node e2 = errs[1];
		Node e2P = parents[1];
		Node e2L = e2.left;
		Node e2R = e2.right;
		if (e1 == head) {
			if (e1 == e2P) { // ���һ
				e1.left = e2L;
				e1.right = e2R;
				e2.right = e1;
				e2.left = e1L;
			} else if (e2P.left == e2) { // �����
				e2P.left = e1;
				e2.left = e1L;
				e2.right = e1R;
				e1.left = e2L;
				e1.right = e2R;
			} else { // �����
				e2P.right = e1;
				e2.left = e1L;
				e2.right = e1R;
				e1.left = e2L;
				e1.right = e2R;
			}
			head = e2;
		} else if (e2 == head) {
			if (e2 == e1P) { // �����
				e2.left = e1L;
				e2.right = e1R;
				e1.left = e2;
				e1.right = e2R;
			} else if (e1P.left == e1) { // �����
				e1P.left = e2;
				e1.left = e2L;
				e1.right = e2R;
				e2.left = e1L;
				e2.right = e1R;
			} else { // �����
				e1P.right = e2;
				e1.left = e2L;
				e1.right = e2R;
				e2.left = e1L;
				e2.right = e1R;
			}
			head = e1;
		} else {
			if (e1 == e2P) {
				if (e1P.left == e1) { // �����
					e1P.left = e2;
					e1.left = e2L;
					e1.right = e2R;
					e2.left = e1L;
					e2.right = e1;
				} else { // �����
					e1P.right = e2;
					e1.left = e2L;
					e1.right = e2R;
					e2.left = e1L;
					e2.right = e1;
				}
			} else if (e2 == e1P) {
				if (e2P.left == e2) { // �����
					e2P.left = e1;
					e2.left = e1L;
					e2.right = e1R;
					e1.left = e2;
					e1.right = e2R;
				} else { // ���ʮ
					e2P.right = e1;
					e2.left = e1L;
					e2.right = e1R;
					e1.left = e2;
					e1.right = e2R;
				}
			} else {
				if (e1P.left == e1) {
					if (e2P.left == e2) { // ���ʮһ
						e1.left = e2L;
						e1.right = e2R;
						e2.left = e1L;
						e2.right = e1R;
						e1P.left = e2;
						e2P.left = e1;
					} else { // ���ʮ��
						e1.left = e2L;
						e1.right = e2R;
						e2.left = e1L;
						e2.right = e1R;
						e1P.left = e2;
						e2P.right = e1;
					}
				} else {
					if (e2P.left == e2) { // ���ʮ��
						e1.left = e2L;
						e1.right = e2R;
						e2.left = e1L;
						e2.right = e1R;
						e1P.right = e2;
						e2P.left = e1;
					} else { // ���ʮ��
						e1.left = e2L;
						e1.right = e2R;
						e2.left = e1L;
						e2.right = e1R;
						e1P.right = e2;
						e2P.right = e1;
					}
				}
			}
		}
		return head;
	}

	// for test -- print tree
	public static void printTree(Node head) {
		System.out.println("Binary Tree:");
		printInOrder(head, 0, "H", 17);
		System.out.println();
	}

	public static void printInOrder(Node head, int height, String to, int len) {
		if (head == null) {
			return;
		}
		printInOrder(head.right, height + 1, "v", len);
		String val = to + head.value + to;
		int lenM = val.length();
		int lenL = (len - lenM) / 2;
		int lenR = len - lenM - lenL;
		val = getSpace(lenL) + val + getSpace(lenR);
		System.out.println(getSpace(height * len) + val);
		printInOrder(head.left, height + 1, "^", len);
	}

	public static String getSpace(int num) {
		String space = " ";
		StringBuffer buf = new StringBuffer("");
		for (int i = 0; i < num; i++) {
			buf.append(space);
		}
		return buf.toString();
	}

	// for test
	public static boolean isBST(Node head) {
		if (head == null) {
			return false;
		}
		Stack<Node> stack = new Stack<Node>();
		Node pre = null;
		while (!stack.isEmpty() || head != null) {
			if (head != null) {
				stack.push(head);
				head = head.left;
			} else {
				head = stack.pop();
				if (pre != null && pre.value > head.value) {
					return false;
				}
				pre = head;
				head = head.right;
			}
		}
		return true;
	}

	public static void main(String[] args) {
		Node head = new Node(5);
		head.left = new Node(3);
		head.right = new Node(7);
		head.left.left = new Node(2);
		head.left.right = new Node(4);
		head.right.left = new Node(6);
		head.right.right = new Node(8);
		head.left.left.left = new Node(1);
		printTree(head);
		System.out.println(isBST(head));

		// ���1, 7 -> e1, 5 -> e2
		System.out.println("situation 1");
		Node head1 = new Node(7);
		head1.left = new Node(3);
		head1.right = new Node(5);
		head1.left.left = new Node(2);
		head1.left.right = new Node(4);
		head1.right.left = new Node(6);
		head1.right.right = new Node(8);
		head1.left.left.left = new Node(1);
		printTree(head1);
		System.out.println(isBST(head1));
		Node res1 = recoverTree(head1);
		printTree(res1);
		System.out.println(isBST(res1));

		// ���2, 6 -> e1, 5 -> e2
		System.out.println("situation 2");
		Node head2 = new Node(6);
		head2.left = new Node(3);
		head2.right = new Node(7);
		head2.left.left = new Node(2);
		head2.left.right = new Node(4);
		head2.right.left = new Node(5);
		head2.right.right = new Node(8);
		head2.left.left.left = new Node(1);
		printTree(head2);
		System.out.println(isBST(head2));
		Node res2 = recoverTree(head2);
		printTree(res2);
		System.out.println(isBST(res2));

		// ���3, 8 -> e1, 5 -> e2
		System.out.println("situation 3");
		Node head3 = new Node(8);
		head3.left = new Node(3);
		head3.right = new Node(7);
		head3.left.left = new Node(2);
		head3.left.right = new Node(4);
		head3.right.left = new Node(6);
		head3.right.right = new Node(5);
		head3.left.left.left = new Node(1);
		printTree(head3);
		System.out.println(isBST(head3));
		Node res3 = recoverTree(head3);
		printTree(res3);
		System.out.println(isBST(res3));

		// ���4, 5 -> e1, 3 -> e2
		System.out.println("situation 4");
		Node head4 = new Node(3);
		head4.left = new Node(5);
		head4.right = new Node(7);
		head4.left.left = new Node(2);
		head4.left.right = new Node(4);
		head4.right.left = new Node(6);
		head4.right.right = new Node(8);
		head4.left.left.left = new Node(1);
		printTree(head4);
		System.out.println(isBST(head4));
		Node res4 = recoverTree(head4);
		printTree(res4);
		System.out.println(isBST(res4));

		// ���5, 5 -> e1, 2 -> e2
		System.out.println("situation 5");
		Node head5 = new Node(2);
		head5.left = new Node(3);
		head5.right = new Node(7);
		head5.left.left = new Node(5);
		head5.left.right = new Node(4);
		head5.right.left = new Node(6);
		head5.right.right = new Node(8);
		head5.left.left.left = new Node(1);
		printTree(head5);
		System.out.println(isBST(head5));
		Node res5 = recoverTree(head5);
		printTree(res5);
		System.out.println(isBST(res5));

		// ���6, 5 -> e1, 4 -> e2
		System.out.println("situation 6");
		Node head6 = new Node(4);
		head6.left = new Node(3);
		head6.right = new Node(7);
		head6.left.left = new Node(2);
		head6.left.right = new Node(5);
		head6.right.left = new Node(6);
		head6.right.right = new Node(8);
		head6.left.left.left = new Node(1);
		printTree(head6);
		System.out.println(isBST(head6));
		Node res6 = recoverTree(head6);
		printTree(res6);
		System.out.println(isBST(res6));

		// ���7, 4 -> e1, 3 -> e2
		System.out.println("situation 7");
		Node head7 = new Node(5);
		head7.left = new Node(4);
		head7.right = new Node(7);
		head7.left.left = new Node(2);
		head7.left.right = new Node(3);
		head7.right.left = new Node(6);
		head7.right.right = new Node(8);
		head7.left.left.left = new Node(1);
		printTree(head7);
		System.out.println(isBST(head7));
		Node res7 = recoverTree(head7);
		printTree(res7);
		System.out.println(isBST(res7));

		// ���8, 8 -> e1, 7 -> e2
		System.out.println("situation 8");
		Node head8 = new Node(5);
		head8.left = new Node(3);
		head8.right = new Node(8);
		head8.left.left = new Node(2);
		head8.left.right = new Node(4);
		head8.right.left = new Node(6);
		head8.right.right = new Node(7);
		head8.left.left.left = new Node(1);
		printTree(head8);
		System.out.println(isBST(head8));
		Node res8 = recoverTree(head8);
		printTree(res8);
		System.out.println(isBST(res8));

		// ���9, 3 -> e1, 2 -> e2
		System.out.println("situation 9");
		Node head9 = new Node(5);
		head9.left = new Node(2);
		head9.right = new Node(7);
		head9.left.left = new Node(3);
		head9.left.right = new Node(4);
		head9.right.left = new Node(6);
		head9.right.right = new Node(8);
		head9.left.left.left = new Node(1);
		printTree(head9);
		System.out.println(isBST(head9));
		Node res9 = recoverTree(head9);
		printTree(res9);
		System.out.println(isBST(res9));

		// ���10, 7 -> e1, 6 -> e2
		System.out.println("situation 10");
		Node head10 = new Node(5);
		head10.left = new Node(3);
		head10.right = new Node(6);
		head10.left.left = new Node(2);
		head10.left.right = new Node(4);
		head10.right.left = new Node(7);
		head10.right.right = new Node(8);
		head10.left.left.left = new Node(1);
		printTree(head10);
		System.out.println(isBST(head10));
		Node res10 = recoverTree(head10);
		printTree(res10);
		System.out.println(isBST(res10));

		// ���11, 6 -> e1, 2 -> e2
		System.out.println("situation 11");
		Node head11 = new Node(5);
		head11.left = new Node(3);
		head11.right = new Node(7);
		head11.left.left = new Node(6);
		head11.left.right = new Node(4);
		head11.right.left = new Node(2);
		head11.right.right = new Node(8);
		head11.left.left.left = new Node(1);
		printTree(head11);
		System.out.println(isBST(head11));
		Node res11 = recoverTree(head11);
		printTree(res11);
		System.out.println(isBST(res11));

		// ���12, 8 -> e1, 2 -> e2
		System.out.println("situation 12");
		Node head12 = new Node(5);
		head12.left = new Node(3);
		head12.right = new Node(7);
		head12.left.left = new Node(8);
		head12.left.right = new Node(4);
		head12.right.left = new Node(6);
		head12.right.right = new Node(2);
		head12.left.left.left = new Node(1);
		printTree(head12);
		System.out.println(isBST(head12));
		Node res12 = recoverTree(head12);
		printTree(res12);
		System.out.println(isBST(res12));

		// ���13, 6 -> e1, 4 -> e2
		System.out.println("situation 13");
		Node head13 = new Node(5);
		head13.left = new Node(3);
		head13.right = new Node(7);
		head13.left.left = new Node(2);
		head13.left.right = new Node(6);
		head13.right.left = new Node(4);
		head13.right.right = new Node(8);
		head13.left.left.left = new Node(1);
		printTree(head13);
		System.out.println(isBST(head13));
		Node res13 = recoverTree(head13);
		printTree(res13);
		System.out.println(isBST(res13));

		// ���14, 8 -> e1, 4 -> e2
		System.out.println("situation 14");
		Node head14 = new Node(5);
		head14.left = new Node(3);
		head14.right = new Node(7);
		head14.left.left = new Node(2);
		head14.left.right = new Node(8);
		head14.right.left = new Node(6);
		head14.right.right = new Node(4);
		head14.left.left.left = new Node(1);
		printTree(head14);
		System.out.println(isBST(head14));
		Node res14 = recoverTree(head14);
		printTree(res14);
		System.out.println(isBST(res14));

	}

}

有多少个矩形相互重叠

平面内有n个矩形, 第i个矩形的左下角坐标为(x1[i], y1[i]), 右上角坐标为(x2[i],y2[i])。如果两个或者多个矩形有公共区域则认为它们是相互重叠的(不考虑边界和角落)。请你计算出平面内重叠矩形数量最多的地方,有多少个矩形相互重叠。

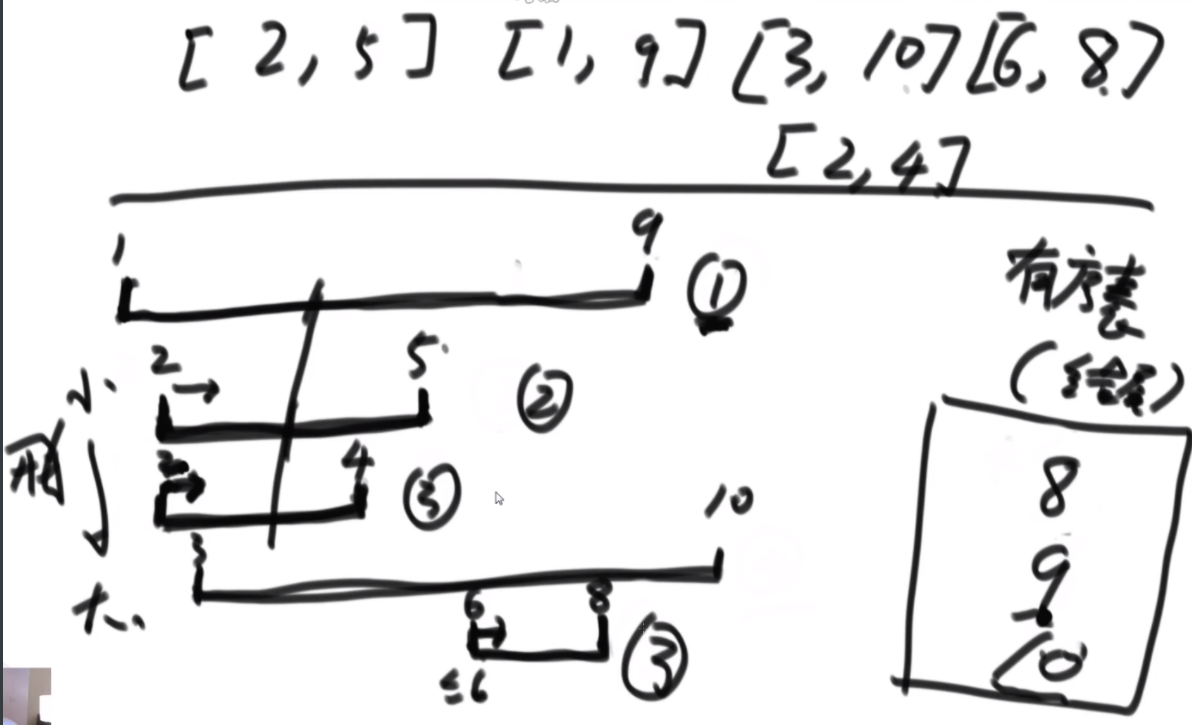
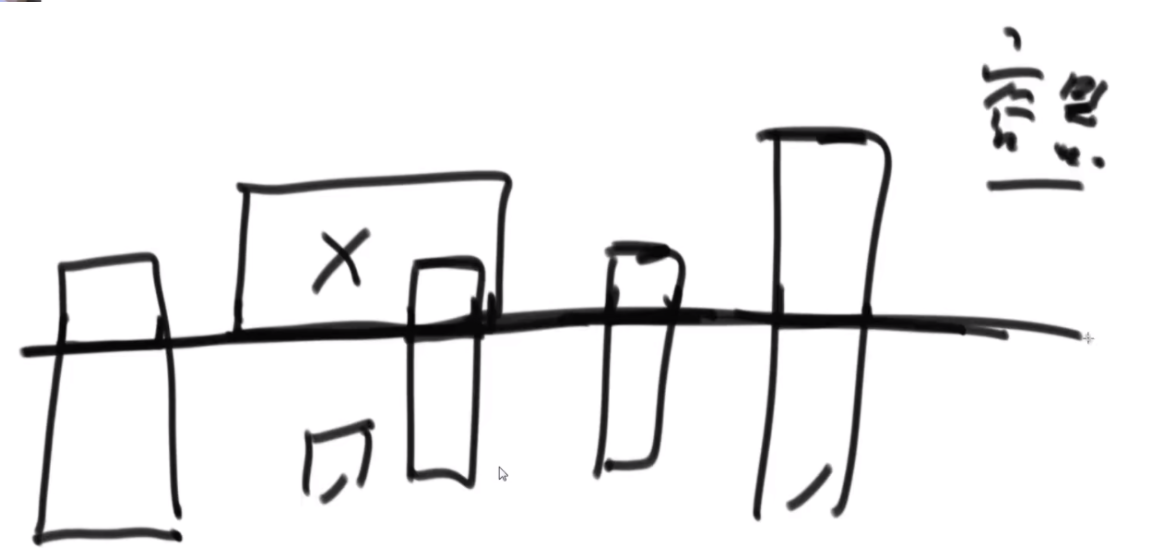
思路：首先把这种二维的东西分解成一维的去考虑，先看线段上是怎么解决的。先给线段排个序，然后从开头最小的开始，第一个直接放入，并且去掉所有结尾小于1的线段，第二个2，5进入的时候去掉所有结尾小于2的，有序表中只存储该线段的结尾大小，以此来判断贯穿最多的线段个数。至于矩形，就先看一次，丢掉所有上边界低于新矩形下边界的，依次进入。进入后再筛一次，丢掉所有结束边界小于开始边界的左右边界的矩形，达成目的。

package class06;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.TreeSet;

public class Problem04_CoverMax {

	public static class Rectangle {
		public int up;
		public int down;
		public int left;
		public int right;

		public Rectangle(int up, int down, int left, int right) {
			this.up = up;
			this.down = down;
			this.left = left;
			this.right = right;
		}

	}

	public static class DownComparator implements Comparator<Rectangle> {
		@Override
		public int compare(Rectangle o1, Rectangle o2) {
			return o1.down - o2.down;
		}
	}

	public static class LeftComparator implements Comparator<Rectangle> {
		@Override
		public int compare(Rectangle o1, Rectangle o2) {
			return o1.left - o2.left;
		}
	}

	public static class RightComparator implements Comparator<Rectangle> {
		@Override
		public int compare(Rectangle o1, Rectangle o2) {
			return o1.right - o2.right;
		}
	}

	public static int maxCover(Rectangle[] recs) {
		if (recs == null || recs.length == 0) {
			return 0;
		}
		Arrays.sort(recs, new DownComparator());
		TreeSet<Rectangle> leftOrdered = new TreeSet<>(new LeftComparator());
		int ans = 0;
		for (int i = 0; i < recs.length; i++) {
			int curDown = recs[i].down;
			int index = i;
			while (recs[index].down == curDown) {
				leftOrdered.add(recs[index]);
				index++;
			}
			i = index;
			removeLowerOnCurDown(leftOrdered, curDown);
			TreeSet<Rectangle> rightOrdered = new TreeSet<>(new RightComparator());
			for (Rectangle rec : leftOrdered) {
				removeLeftOnCurLeft(rightOrdered, rec.left);
				rightOrdered.add(rec);
				ans = Math.max(ans, rightOrdered.size());
			}
		}
		return ans;
	}

	public static void removeLowerOnCurDown(TreeSet<Rectangle> set, int curDown) {
		List<Rectangle> removes = new ArrayList<>();
		for (Rectangle rec : set) {
			if (rec.up <= curDown) {
				removes.add(rec);
			}
		}
		for (Rectangle rec : removes) {
			set.remove(rec);
		}
	}

	public static void removeLeftOnCurLeft(TreeSet<Rectangle> rightOrdered, int curLeft) {
		List<Rectangle> removes = new ArrayList<>();
		for (Rectangle rec : rightOrdered) {
			if (rec.right > curLeft) {
				break;
			}
			removes.add(rec);
		}
		for (Rectangle rec : removes) {
			rightOrdered.remove(rec);
		}
	}

}

p37&p38:

str2是不是str1的旋变字符串

一个字符串可以分解成多种二叉树结构。如果str长度为 1，认为不可分解。如果str长度为N(N>1)，左部分长度可以为 1~N-1，剩下的为右部分的长度。左部分和右部分都可以按照同样的逻辑，继续分解。形成的所有结构都是str的二叉树结构。比如，字符串"abcd"，可以分解成以下五种结构，

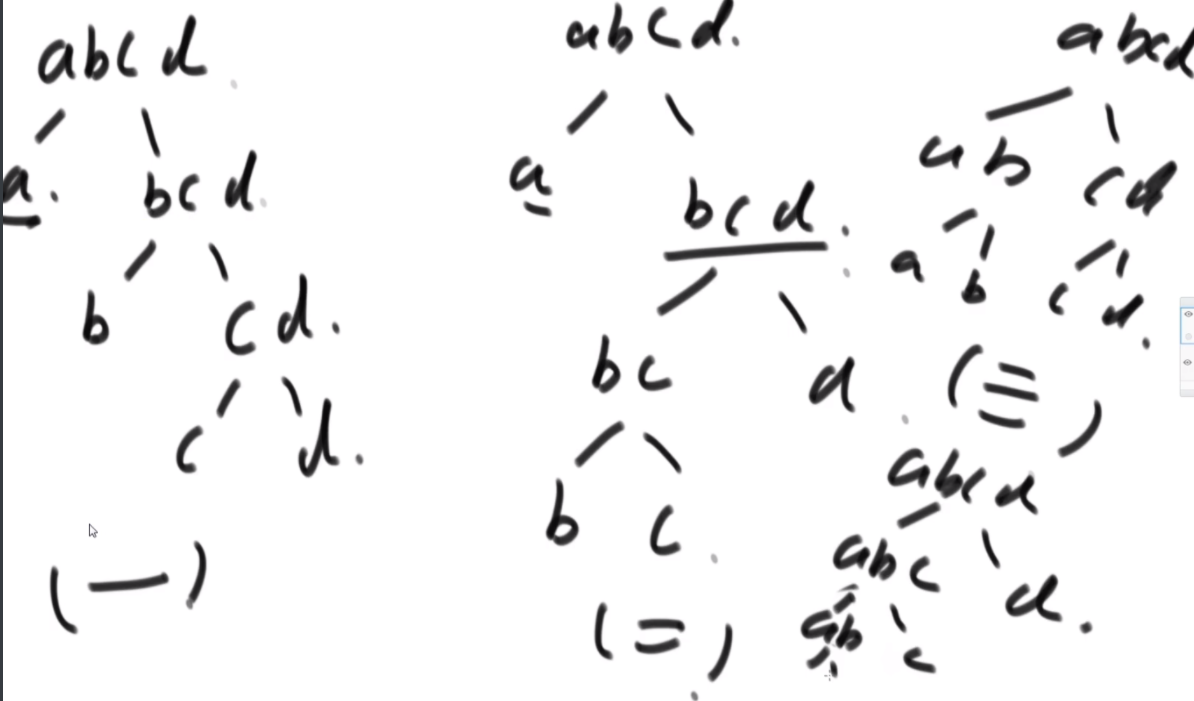
任何一个str的二叉树结构中，如果两个节点有共同的父节点，那么这两个节点可以交换位置，这两个节点叫作一个交换组。一个结构会有很多交换组，每个交换组都可以选择进行交换或者不交换，最终形成一个新的结构，这个新结构所代表的字符串叫作 str的旋变字符串。比如， 在上面的结构五中，交换组有a和b、ab和c、abc和d。如果让a和b的组交换；让ab和c的组不交 换；让abc和d的组交换，形成的结构如图这个新结构所代表的字符串为"dbac"，叫作"abcd"的旋变字符串。也就是说，一个字符串str的旋变字符串是非常多的，str 可以形成很多种结构，每一种结构都有很多交换组，每一个交换组都可以选择交换或者不交换，形成的每一个新的字符串都叫 str的旋变字符串。

给定两个字符串str1和str2，判断str2是不是str1的旋变字符串。

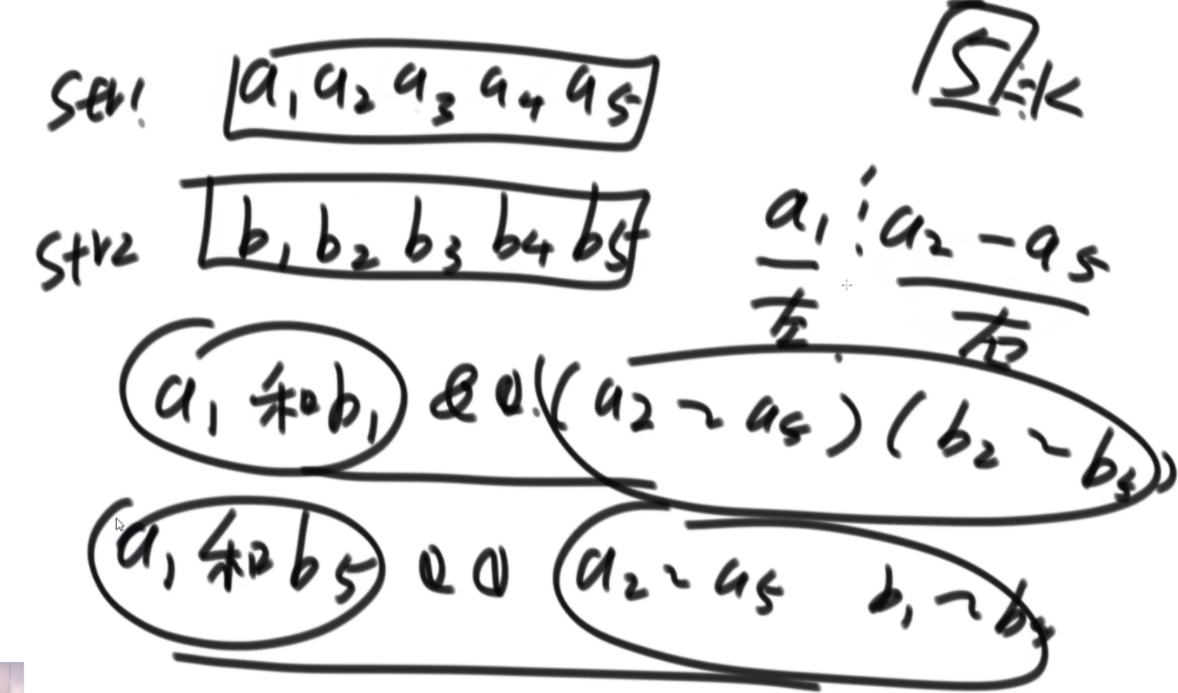
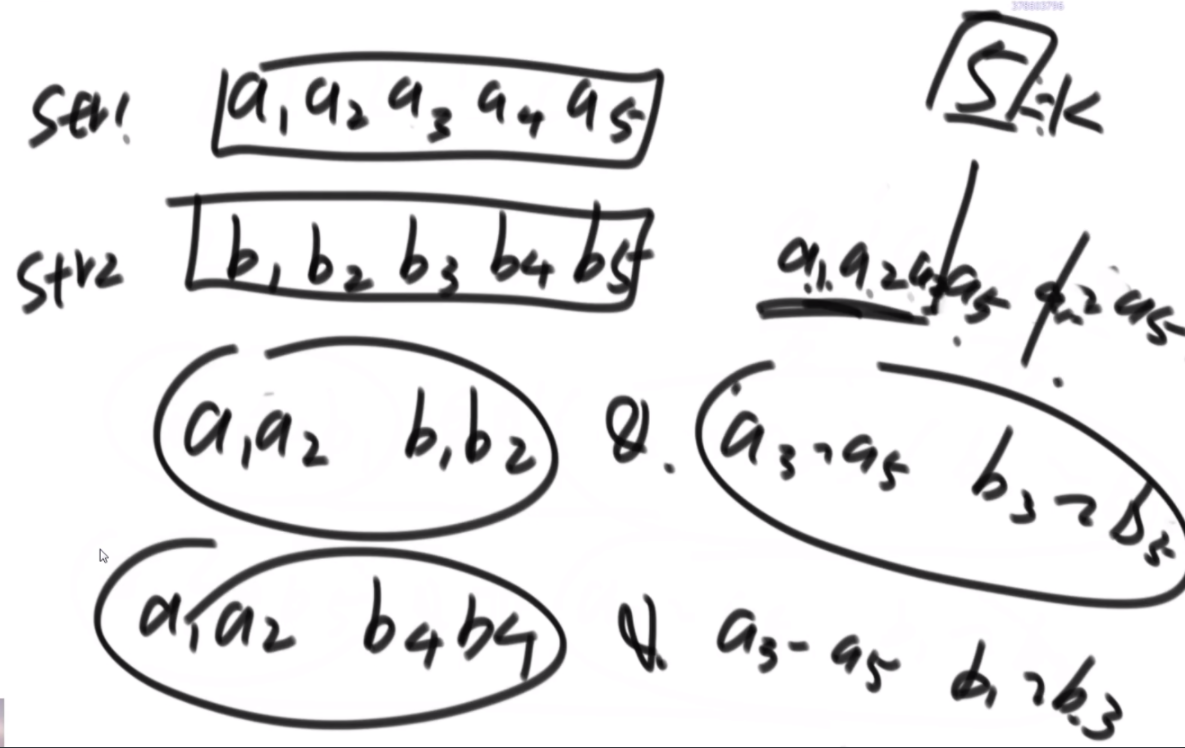
思路：如果是之前的话，str1的L1,R1和str2的L2,R2会有四个参数，现在改成str1的L1开始和str2的L2开始以及长度K，这样是三维的。因为旋变字符串必须是长度一样而且字符种类以及个数一样，因此长度直接用K代替即可。

然后是分析可能性，首先是K从1开始逐渐长，K=1时，判断a1和b1&&a2..a5和b2..b5，以及旋转后的情况，即判断a1和b5&&a2..a5和b1..b4.总之就是不交换的情况比较一次，交换的情况比较一次，有一个是true就是true。

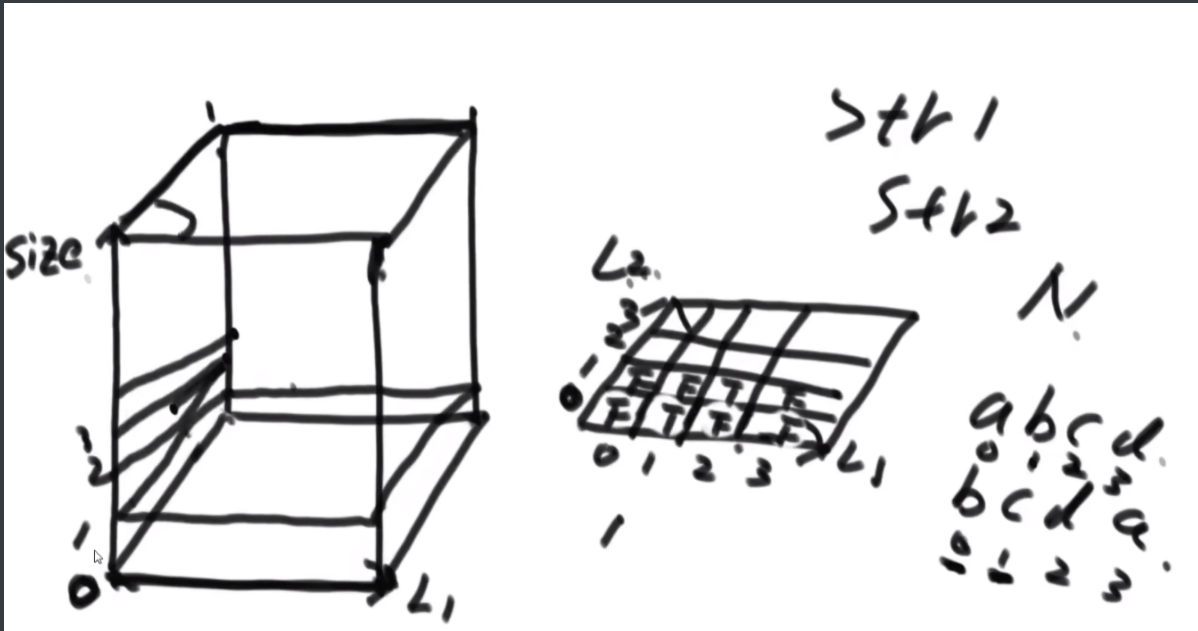
每次递归传入的size是逐渐变小的，先把图形勾勒出来，然后记住这个每个面有些地方会用不到，在for循环的时候要去掉。

package class08;

public class Problem01_ScrambleString {

	public static boolean sameTypeSameNumber(char[] str1, char[] str2) {
		if (str1.length != str2.length) {
			return false;
		}
		int[] map = new int[256];
		for (int i = 0; i < str1.length; i++) {
			map[str1[i]]++;
		}
		for (int i = 0; i < str2.length; i++) {
			if (--map[str2[i]] < 0) {
				return false;
			}
		}
		return true;
	}

	public static boolean isScramble1(String s1, String s2) {
		if ((s1 == null && s2 != null) || (s1 != null && s2 == null)) {
			return false;
		}
		if (s1 == null && s2 == null) {
			return true;
		}
		if (s1.equals(s2)) {
			return true;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		if (!sameTypeSameNumber(str1, str2)) {
			return false;
		}
		int N = s1.length();
		return process(str1, str2, 0, 0, N);
	}

	// 返回str1[从L1开始往右长度为size的子串]和str2[从L2开始往右长度为size的子串]是否互为旋变字符串
	// 在str1中的这一段和str2中的这一段一定是等长的，所以只用一个参数size
	public static boolean process(char[] str1, char[] str2, int L1, int L2,
			int size) {
		if (size == 1) {
			return str1[L1] == str2[L2];
		}
		// 枚举每一种情况，有一个计算出互为旋变就返回true。都算不出来最后返回false
		for (int leftPart = 1; leftPart < size; leftPart++) {
			if (
			// str1: 左1 右1
			// str2: 左2 右2
			// (左1 左2)&&(右1 右2)
			(process(str1, str2, L1, L2, leftPart) && process(str1, str2,
					L1 + leftPart, L2 + leftPart, size - leftPart))
					|| 
			// (左1 右2)&&(右1 左2)	
			(process(str1, str2, L1, L2 + size - leftPart, leftPart) && process(
							str1, str2, L1 + leftPart, L2, size - leftPart))) {
				return true;
			}
		}
		return false;
	}

	public static boolean isScramble2(String s1, String s2) {
		if ((s1 == null && s2 != null) || (s1 != null && s2 == null)) {
			return false;
		}
		if (s1 == null && s2 == null) {
			return true;
		}
		if (s1.equals(s2)) {
			return true;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		if (!sameTypeSameNumber(str1, str2)) {
			return false;
		}
		int N = s1.length();
		boolean[][][] dp = new boolean[N][N][N + 1];
		for (int L1 = 0; L1 < N; L1++) {
			for (int L2 = 0; L2 < N; L2++) {
				dp[L1][L2][1] = str1[L1] == str2[L2];
			}
		}
		// 第一层for循环含义是：依次填size=2层、size=3层..size=N层，每一层都是一个二维平面
		// 第二、三层for循环含义是：在具体的一层，整个面都要填写，所以用两个for循环去填一个二维面
		// L1的取值氛围是[0,N-size]，因为从L1出发往右长度为size的子串，L1是不能从N-size+1出发的，这样往右就不够size个字符了
		// L2的取值范围同理
		// 第4层for循环完全是递归函数怎么写，这里就怎么改的
		for (int size = 2; size <= N; size++) {
			for (int L1 = 0; L1 <= N - size; L1++) {
				for (int L2 = 0; L2 <= N - size; L2++) {
					for (int leftPart = 1; leftPart < size; leftPart++) {
						if ((dp[L1][L2][leftPart] && dp[L1 + leftPart][L2
								+ leftPart][size - leftPart])
								|| (dp[L1][L2 + size - leftPart][leftPart] && dp[L1
										+ leftPart][L2][size - leftPart])) {
							dp[L1][L2][size] = true;
							break;
						}
					}
				}
			}
		}
		return dp[0][0][N];
	}

	public static void main(String[] args) {
		String test1 = "abcd";
		String test2 = "cdab";
		System.out.println(isScramble1(test1, test2));
		System.out.println(isScramble2(test1, test2));

		test1 = "abcd";
		test2 = "cadb";
		System.out.println(isScramble1(test1, test2));
		System.out.println(isScramble2(test1, test2));

		test1 = "bcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcdebcde";
		test2 = "ebcdeebcdebebcdebcdebcdecdebcbcdcdebcddebcbdebbbcdcdebcdeebcdebcdeebcddeebccdebcdbcdebcd";
		// System.out.println(isScramble1(test1, test2));
		System.out.println(isScramble2(test1, test2));
	}

}

str1的子串中含有str2所有字符的最小子串长度

给定字符串str1和str2，求str1的子串中含有str2所有字符的最小子串长度

【举例】

str1="abcde"，str2="ac" 因为"abc"包含 str2 所有的字符，并且在满足这一条件的str1的所有子串中，"abc"是最短的，返回3。

str1="12345"，str2="344" 最小包含子串不存在，返回0。

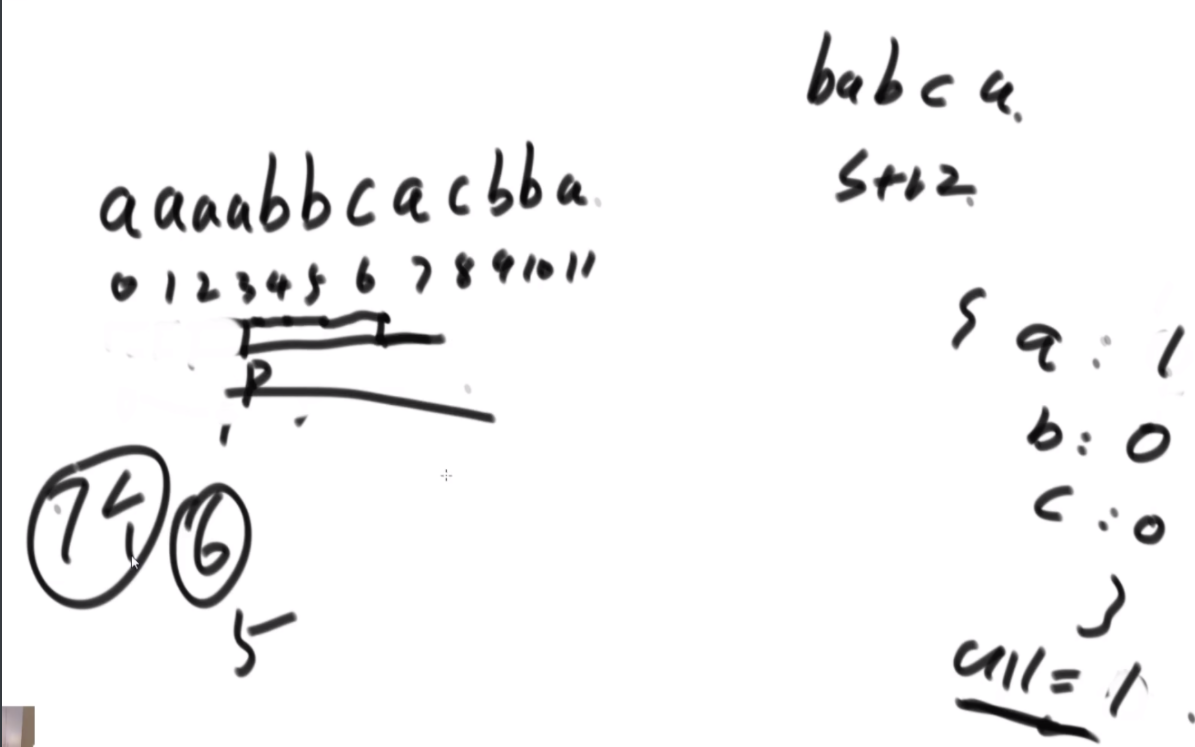
思路：首先是从0开始往右走，用一个map记录每个字符欠了多少个，一直走到一个不欠，是0-6，然后左边开始走，变成了1-6，此时a少了一个，但是还是不欠，因为本来就给多了，如此而来形成了一个窗口，记录窗口最小的长度就行了。

package class08;

public class Problem02_MinWindowLength {

	public static int minLength(String str1, String str2) {
		if (str1 == null || str2 == null || str1.length() < str2.length()) {
			return 0;
		}
		char[] chas1 = str1.toCharArray();
		char[] chas2 = str2.toCharArray();
		int[] map = new int[256];
		for (int i = 0; i != chas2.length; i++) {
			map[chas2[i]]++;
		}
		int left = 0;
		int right = 0;
		int match = chas2.length;
		int minLen = Integer.MAX_VALUE;
		while (right != chas1.length) {
			map[chas1[right]]--;
			if (map[chas1[right]] >= 0) {
				match--;
			}
			if (match == 0) {
				while (map[chas1[left]] < 0) {
					map[chas1[left++]]++;
				}
				minLen = Math.min(minLen, right - left + 1);
				match++;
				map[chas1[left++]]++;
			}
			right++;
		}
		return minLen == Integer.MAX_VALUE ? 0 : minLen;
	}

	public static void main(String[] args) {
		String str1 = "adabbca";
		String str2 = "acb";
		System.out.println(minLength(str1, str2));

	}

}

LFU缓存替换算法

一个缓存结构需要实现如下功能

void set(int key, int value)：加入或修改key对应的value

int get(int key)：查询key对应的value值

但是缓存中最多放K条记录，如果新的第K+1条记录要加入，就需要根据策略删掉一条记录，然后才能把新记录加入。这个策略为：在缓存结构的K条记录中，哪一个key从进入缓存结构的时刻开始，被调用set或者get的次数最少，就删掉这个key的记录；如果调用次数最少的key有多个，上次调用发生最早的key被删除。这就是LFU缓存替换算法。实现这个结构，K作为参数给出。

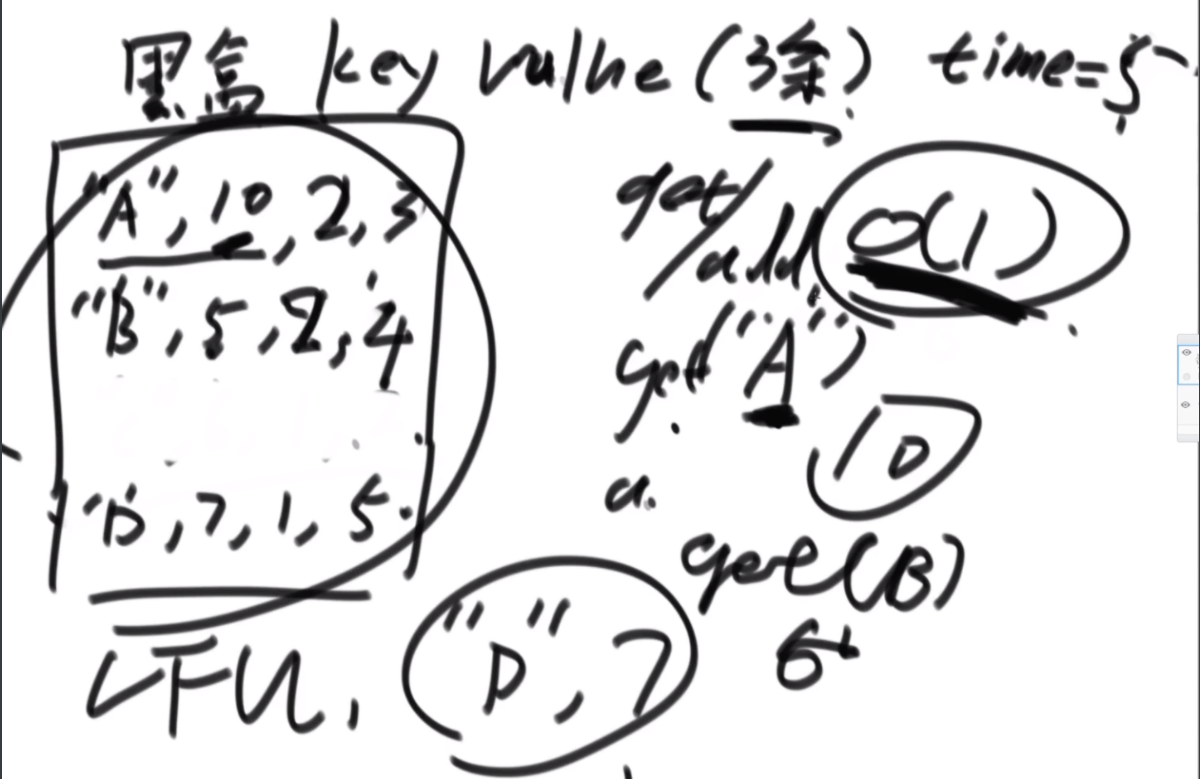
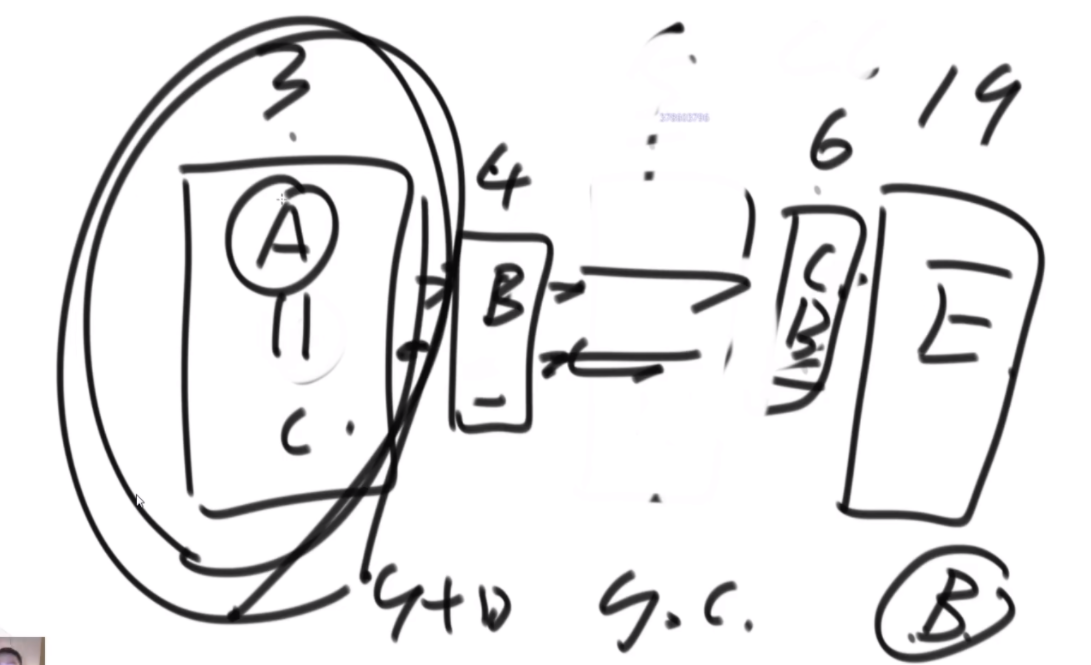
思路：这个题是很难的 用的是双向二维循环列表。首先是搞一个桶，然后里面保存的是(A,10)，字符串和对应的值，另搞一个map去记录这些，key是字符串，value是这些节点的内存地址，这样查找的时间就是O(1)。然后搞一个桶，第一个桶代表访问次数为1的节点，每个桶内部是双向循环链表，如果里面有节点又被访问了一次，那么这个节点被拿到代表访问次数为2的桶里，桶与桶之间也是用双向链表链接，如果一个桶空了就销毁，如果一个桶没有就新建。

package class08;

import java.util.HashMap;

public class Problem03_LFU {

	// 节点的数据结构
	public static class Node {
		public Integer key;
		public Integer value;
		public Integer times; // 这个节点发生get或者set的次数总和
		public Node up; // 节点之间是双向链表所以有上一个节点
		public Node down;// 节点之间是双向链表所以有下一个节点

		public Node(int key, int value, int times) {
			this.key = key;
			this.value = value;
			this.times = times;
		}
	}

	// 桶结构
	public static class NodeList {
		public Node head; // 桶的头节点
		public Node tail; // 桶的尾节点
		public NodeList last; // 桶之间是双向链表所以有前一个桶
		public NodeList next; // 桶之间是双向链表所以有后一个桶

		public NodeList(Node node) {
			head = node;
			tail = node;
		}

		// 把一个新的节点加入这个桶，新的节点都放在顶端变成新的头部
		public void addNodeFromHead(Node newHead) {
			newHead.down = head;
			head.up = newHead;
			head = newHead;
		}

		// 判断这个桶是不是空的
		public boolean isEmpty() {
			return head == null;
		}

		// 删除node节点并保证node的上下环境重新连接
		public void deleteNode(Node node) {
			if (head == tail) {
				head = null;
				tail = null;
			} else {
				if (node == head) {
					head = node.down;
					head.up = null;
				} else if (node == tail) {
					tail = node.up;
					tail.down = null;
				} else {
					node.up.down = node.down;
					node.down.up = node.up;
				}
			}
			node.up = null;
			node.down = null;
		}
	}

	// 总的缓存结构
	public static class LFUCache {
		private int capacity; // 缓存的大小限制，即K
		private int size; // 缓存目前有多少个节点
		private HashMap<Integer, Node> records;// 表示key(Integer)由哪个节点(Node)代表
		private HashMap<Node, NodeList> heads; // 表示节点(Node)在哪个桶(NodeList)里
		private NodeList headList; // 整个结构中位于最左的桶

		public LFUCache(int K) {
			this.capacity = K;
			this.size = 0;
			this.records = new HashMap<>();
			this.heads = new HashMap<>();
			headList = null;
		}

		// removeNodeList：刚刚减少了一个节点的桶
		// 这个函数的功能是，判断刚刚减少了一个节点的桶是不是已经空了。
		// 1）如果不空，什么也不做
		//
		// 2)如果空了，removeNodeList还是整个缓存结构最左的桶(headList)。
		// 删掉这个桶的同时也要让最左的桶变成removeNodeList的下一个。
		//
		// 3)如果空了，removeNodeList不是整个缓存结构最左的桶(headList)。
		// 把这个桶删除，并保证上一个的桶和下一个桶之间还是双向链表的连接方式
		//
		// 函数的返回值表示刚刚减少了一个节点的桶是不是已经空了，空了返回true；不空返回false
		private boolean modifyHeadList(NodeList removeNodeList) {
			if (removeNodeList.isEmpty()) {
				if (headList == removeNodeList) {
					headList = removeNodeList.next;
					if (headList != null) {
						headList.last = null;
					}
				} else {
					removeNodeList.last.next = removeNodeList.next;
					if (removeNodeList.next != null) {
						removeNodeList.next.last = removeNodeList.last;
					}
				}
				return true;
			}
			return false;
		}

		// 函数的功能
		// node这个节点的次数+1了，这个节点原来在oldNodeList里。
		// 把node从oldNodeList删掉，然后放到次数+1的桶中
		// 整个过程既要保证桶之间仍然是双向链表，也要保证节点之间仍然是双向链表
		private void move(Node node, NodeList oldNodeList) {
			oldNodeList.deleteNode(node);
			// preList表示次数+1的桶的前一个桶是谁
			// 如果oldNodeList删掉node之后还有节点，oldNodeList就是次数+1的桶的前一个桶
			// 如果oldNodeList删掉node之后空了，oldNodeList是需要删除的，所以次数+1的桶的前一个桶，是oldNodeList的前一个
			NodeList preList = modifyHeadList(oldNodeList) ? oldNodeList.last
					: oldNodeList;
			// nextList表示次数+1的桶的后一个桶是谁
			NodeList nextList = oldNodeList.next;
			if (nextList == null) {
				NodeList newList = new NodeList(node);
				if (preList != null) {
					preList.next = newList;
				}
				newList.last = preList;
				if (headList == null) {
					headList = newList;
				}
				heads.put(node, newList);
			} else {
				if (nextList.head.times.equals(node.times)) {
					nextList.addNodeFromHead(node);
					heads.put(node, nextList);
				} else {
					NodeList newList = new NodeList(node);
					if (preList != null) {
						preList.next = newList;
					}
					newList.last = preList;
					newList.next = nextList;
					nextList.last = newList;
					if (headList == nextList) {
						headList = newList;
					}
					heads.put(node, newList);
				}
			}
		}

		public void set(int key, int value) {
			if (records.containsKey(key)) {
				Node node = records.get(key);
				node.value = value;
				node.times++;
				NodeList curNodeList = heads.get(node);
				move(node, curNodeList);
			} else {
				if (size == capacity) {
					Node node = headList.tail;
					headList.deleteNode(node);
					modifyHeadList(headList);
					records.remove(node.key);
					heads.remove(node);
					size--;
				}
				Node node = new Node(key, value, 1);
				if (headList == null) {
					headList = new NodeList(node);
				} else {
					if (headList.head.times.equals(node.times)) {
						headList.addNodeFromHead(node);
					} else {
						NodeList newList = new NodeList(node);
						newList.next = headList;
						headList.last = newList;
						headList = newList;
					}
				}
				records.put(key, node);
				heads.put(node, headList);
				size++;
			}
		}

		public Integer get(int key) {
			if (!records.containsKey(key)) {
				return null;
			}
			Node node = records.get(key);
			node.times++;
			NodeList curNodeList = heads.get(node);
			move(node, curNodeList);
			return node.value;
		}

	}
}

环形加油站

N个加油站组成一个环形，给定两个长度都是N的非负数组 oil和dis(N>1)，oil[i]代表第i个加油站存的油可以跑多少千米，dis[i]代表第i个加油站到环中下一个加油站相隔多少千米。假设你有一辆油箱足够大的车，初始时车里没有油。如果车从第i个加油站出发，最终可以回到这个加油站，那么第i个加油站就算良好出发点，否则就不算。请返回长度为N的boolean型数组res，res[i]代表第 i 个加油站是不是良好出发点。

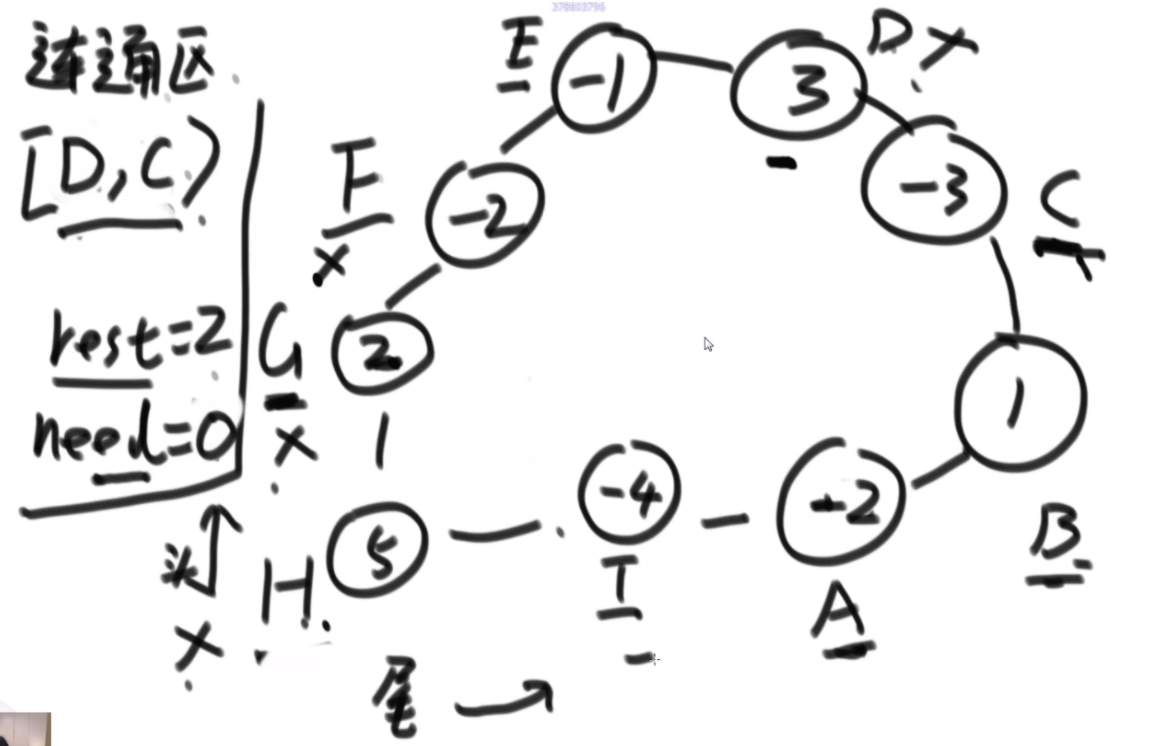
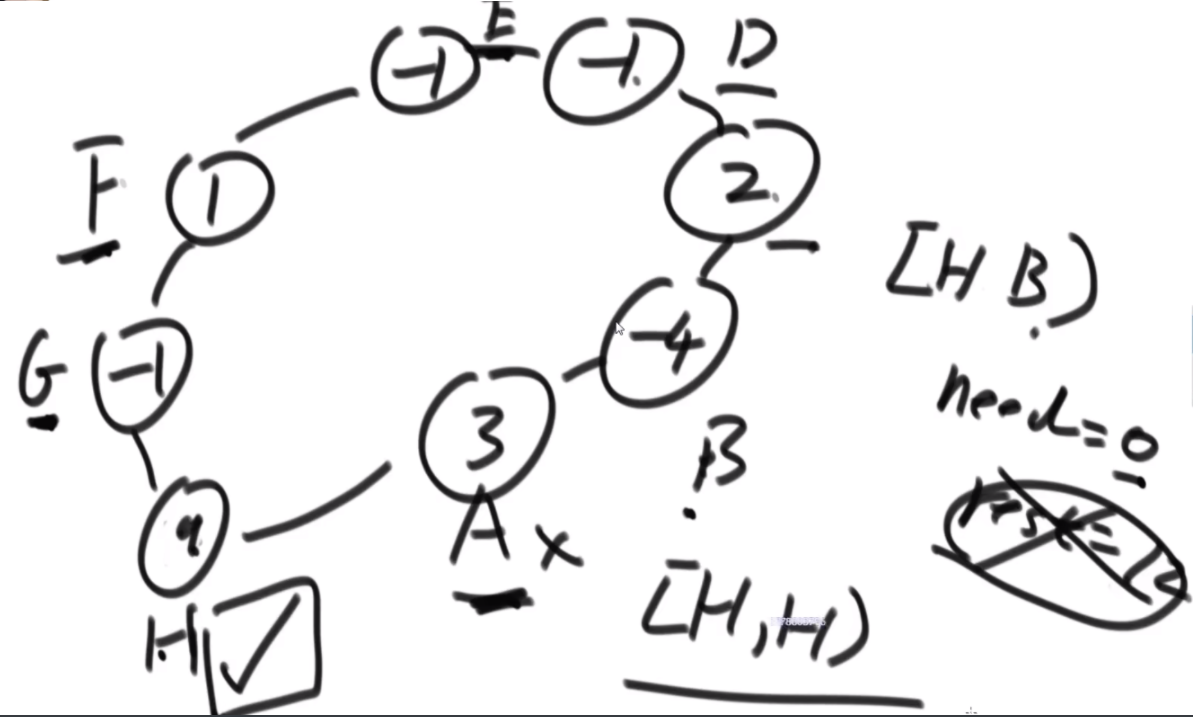
思路：rest代表通过联通区还剩下多少油，need代表通过联通区 需要多少油，权能值数组代表这个油站的油量-这个油站的距离，从H出发，通过I，rest还剩1，但是A需要2个油，联通区没有全覆盖，说明H不是良好出发点，继续往上找点尝试，将出发点变成G，此时rest变成3.然后扩充到G,B，和G,C，rest等于2，C扩不到，那么G也不是良好出发点，顺时针继续找，但是F是负数，那么need等于2，因为F当时没接上，如果后面的节点还要再接需要承担F的油费，联通区一直扩到D，此时3抵了F和E欠下的，rest还是2，但是依旧扩不到C，而且C是联通区的末端，发现没有任何一个良好出发点，直接GG，C、B、A、I不用验了。因为之前为啥他们在联通区里呢？是因为带着有盈余的点冲过他们的，如果这样都不行，更别说他们没有盈余的时候只靠自己了，更不行了。

package class08;

public class Problem04_GasStations {

	public static boolean[] stations(int[] dis, int[] oil) {
		if (dis == null || oil == null || dis.length < 2
				|| dis.length != oil.length) {
			return null;
		}
		int init = changeDisArrayGetInit(dis, oil);
		return init == -1 ? new boolean[dis.length] : enlargeArea(dis, init);
	}

	public static int changeDisArrayGetInit(int[] dis, int[] oil) {
		int init = -1;
		for (int i = 0; i < dis.length; i++) {
			dis[i] = oil[i] - dis[i];
			if (dis[i] >= 0) {
				init = i;
			}
		}
		return init;
	}

	public static boolean[] enlargeArea(int[] dis, int init) {
		boolean[] res = new boolean[dis.length];
		int start = init;
		int end = nextIndex(init, dis.length);
		int need = 0;
		int rest = 0;
		do {
			// 当前来到的start已经在连通区域中，可以确定后续的开始点一定无法转完一圈
			if (start != init && start == lastIndex(end, dis.length)) {
				break;
			}
			// 当前来到的start不在连通区域中，就扩充连通区域
			if (dis[start] < need) { // 从当前start出发，无法到达initial点
				need -= dis[start];
			} else { // 如start可以到达initial点，扩充连通区域的结束点
				rest += dis[start] - need;
				need = 0;
				while (rest >= 0 && end != start) {
					rest += dis[end];
					end = nextIndex(end, dis.length);
				}
				// 如果连通区域已经覆盖整个环，当前的start是良好出发点，进入2阶段
				if (rest >= 0) {
					res[start] = true;
					connectGood(dis, lastIndex(start, dis.length), init, res);
					break;
				}
			}
			start = lastIndex(start, dis.length);
		} while (start != init);
		return res;
	}

	// 已知start的next方向上有一个良好出发点
	// start如果可以达到这个良好出发点，那么从start出发一定可以转一圈
	public static void connectGood(int[] dis, int start, int init, boolean[] res) {
		int need = 0;
		while (start != init) {
			if (dis[start] < need) {
				need -= dis[start];
			} else {
				res[start] = true;
				need = 0;
			}
			start = lastIndex(start, dis.length);
		}
	}

	public static int lastIndex(int index, int size) {
		return index == 0 ? (size - 1) : index - 1;
	}

	public static int nextIndex(int index, int size) {
		return index == size - 1 ? 0 : (index + 1);
	}

	// for test
	public static boolean[] test(int[] dis, int[] oil) {
		if (dis == null || oil == null || dis.length < 2
				|| dis.length != oil.length) {
			return null;
		}
		boolean[] res = new boolean[dis.length];
		for (int i = 0; i < dis.length; i++) {
			dis[i] = oil[i] - dis[i];
		}
		for (int i = 0; i < dis.length; i++) {
			res[i] = canWalkThrough(dis, i);
		}
		return res;
	}

	// for test
	public static boolean canWalkThrough(int[] arr, int index) {
		int sum = 0;
		for (int i = 0; i < arr.length; i++) {
			sum += arr[index];
			if (sum < 0) {
				return false;
			}
			index = nextIndex(index, arr.length);
		}
		return true;
	}

	// for test
	public static void printArray(int[] dis, int[] oil) {
		for (int i = 0; i < dis.length; i++) {
			System.out.print(oil[i] - dis[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void printBooleanArray(boolean[] arr) {
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static int[] generateArray(int size, int max) {
		int[] res = new int[size];
		for (int i = 0; i < res.length; i++) {
			res[i] = (int) (Math.random() * max);
		}
		return res;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		int[] res = new int[arr.length];
		for (int i = 0; i < res.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(boolean[] res1, boolean[] res2) {
		for (int i = 0; i < res1.length; i++) {
			if (res1[i] != res2[i]) {
				return false;
			}
		}
		return true;
	}

	public static void main(String[] args) {
		int max = 20;
		for (int i = 0; i < 5000000; i++) {
			int size = (int) (Math.random() * 20) + 2;
			int[] dis = generateArray(size, max);
			int[] oil = generateArray(size, max);
			int[] dis1 = copyArray(dis);
			int[] oil1 = copyArray(oil);
			int[] dis2 = copyArray(dis);
			int[] oil2 = copyArray(oil);
			boolean[] res1 = stations(dis1, oil1);
			boolean[] res2 = test(dis2, oil2);
			if (!isEqual(res1, res2)) {
				printArray(dis, oil);
				printBooleanArray(res1);
				printBooleanArray(res2);
				System.out.println("what a fucking day!");
				break;
			}
		}
	}

}

p36:

字符串的正则匹配

判定一个由[a-z]字符构成的字符串和一个包含'.'和''通配符的字符串是否匹配。通配符'.'匹配任意单一字符,''匹配任意多个字符包括0个字符。 字符串长度不会超过100，字符串不为空。

输入描述： 字符串 str 和包含通配符的字符串 pattern。1 <= 字符串长度 <= 100

输出描述： true 表示匹配，false 表示不匹配

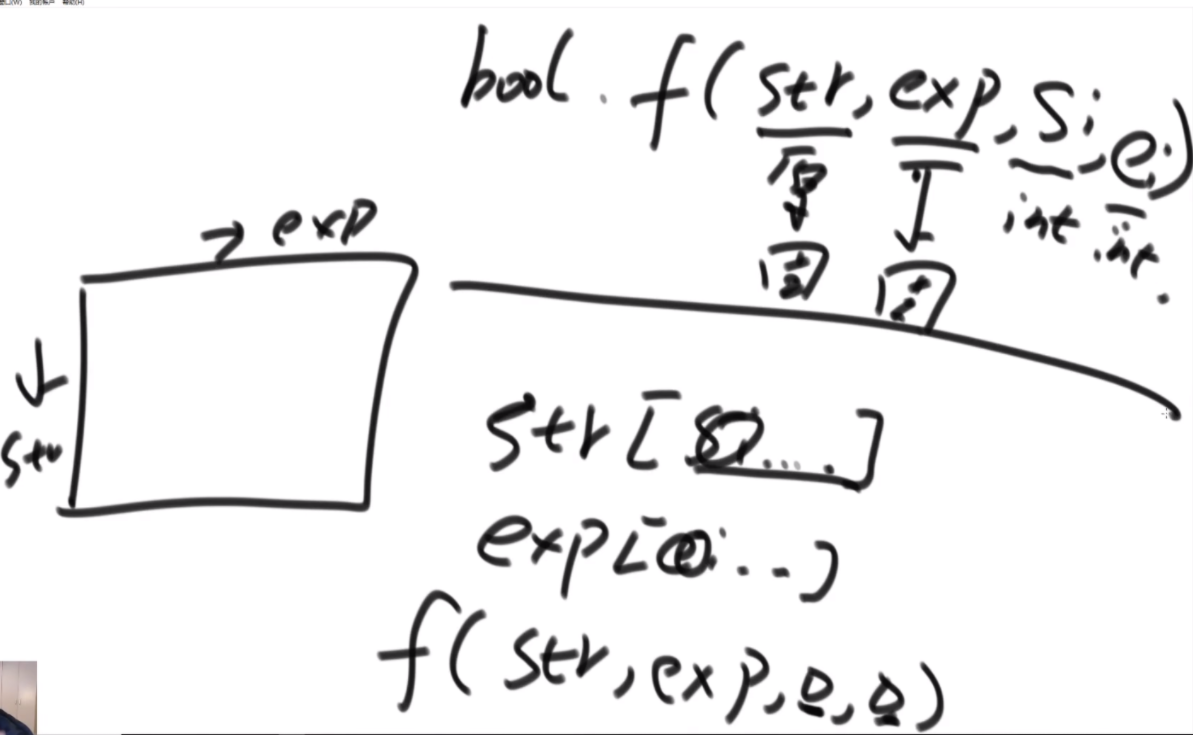
思路：首先是分析如何暴力递归，每次取判断下一个是不是*号，如果不是的话很好处理，如果是的话就得通过si自增来控制a的个数，并且while循环会少一种全是a的解，因此最后的return是一个process，补充最后一种情况的作用。

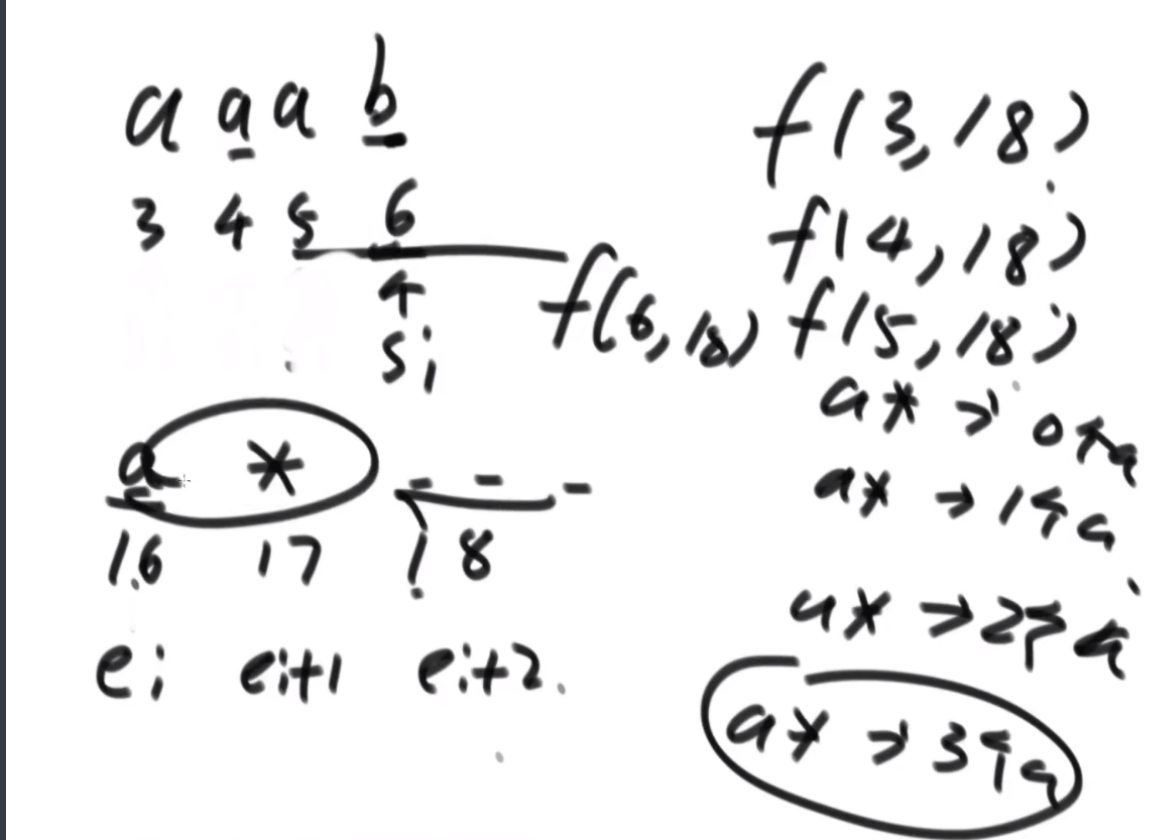
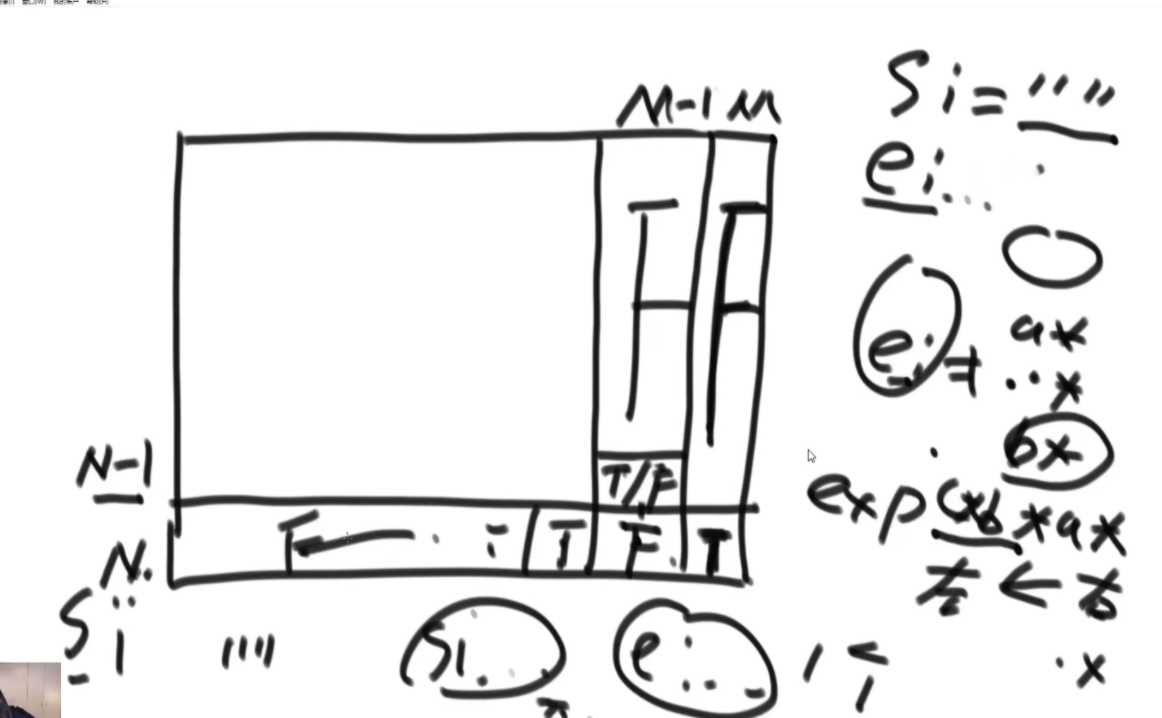
如何改成动态规划：这个题的base case不是很全，隐藏在了这个小的if判断中，因此分析后发现每个点需要自己右下的点和往右两列和自己一行的往下一整列的值，如左图所示，因此需要先搞两列和最后一行才能从倒数第二行从右往左从下往上的去更新。如果dp中ei遇到是*的直接不去理，并且认为是false，因为用不到，然后最后两列可以看出来，最后一行是只有一种情况是连续的exp可以表示0个字符，这个需要单独去判断。

package class07;

public class Problem01_RegularExpressionMatch {

	public static boolean isValid(char[] s, char[] e) {
		for (int i = 0; i < s.length; i++) {
			if (s[i] == '*' || s[i] == '.') {
				return false;
			}
		}
		for (int i = 0; i < e.length; i++) {
			// 如果当前字符是*且是第一个字符或者前一个字符也是*那么exp不合法
			if (e[i] == '*' && (i == 0 || e[i - 1] == '*')) {
				return false;
			}
		}
		return true;
	}

	public static boolean isMatch(String str, String exp) {
		if (str == null || exp == null) {
			return false;
		}
		char[] s = str.toCharArray();
		char[] e = exp.toCharArray();
		return isValid(s, e) ? process(s, e, 0, 0) : false; //0 0位置因为做过有效性检查 所以不用判断
	}

	// s[si...]能否被e[ei...]配出来
	// 必须保证ei压中的字符不是*  *要配合别的字符使用
	// 这里改成记忆化搜索的时候，ei压中*的时候不去管 因为用不到？
	public static boolean process(char[] s, char[] e, int si, int ei) {
		// base case  exp已经耗尽 必须s也耗尽才行
		if (ei == e.length) {
			return si == s.length;
		}
		// 可能性一，ei+1位置不是*
		if (ei + 1 == e.length || e[ei + 1] != '*') {
			//3个条件： si必须还有字符   ei和si相等 或者 ei是.    返回下一个的递归
			return si != s.length && (e[ei] == s[si] || e[ei] == '.') && process(s, e, si + 1, ei + 1);
		}
		// 可能性二，ei+1位置是*
		while (si != s.length && (e[ei] == s[si] || e[ei] == '.')) {
			if (process(s, e, si, ei + 2)) { //si不动 ei+2 意味着a*等价于0个a ei继续往后走看看后面能不能匹配si
				return true;
			} //如果0个a行不通 那么si++  相当于ei这个*是1个a 
			si++;
		}
		//因为3个a的没试过，用这个语句去尝试。
		return process(s, e, si, ei + 2);
	}

	public static boolean isMatchDP(String str, String exp) {
		if (str == null || exp == null) {
			return false;
		}
		char[] s = str.toCharArray();
		char[] e = exp.toCharArray();
		if (!isValid(s, e)) {
			return false;
		}
		boolean[][] dp = initDPMap(s, e);
		for (int i = s.length - 1; i > -1; i--) {
			for (int j = e.length - 2; j > -1; j--) {
				if (e[j + 1] != '*') {
					dp[i][j] = (s[i] == e[j] || e[j] == '.') && dp[i + 1][j + 1];
				} else {
					int si = i;
					while (si != s.length && (s[si] == e[j] || e[j] == '.')) {
						if (dp[si][j + 2]) {
							dp[i][j] = true;
							break;
						}
						si++;
					}
					if (dp[i][j] != true) {
						dp[i][j] = dp[si][j + 2];
					}
				}
			}
		}
		return dp[0][0];
	}

	public static boolean[][] initDPMap(char[] s, char[] e) {
		int slen = s.length;
		int elen = e.length;
		boolean[][] dp = new boolean[slen + 1][elen + 1];
		dp[slen][elen] = true;
		for (int j = elen - 2; j > -1; j = j - 2) {
			if (e[j] != '*' && e[j + 1] == '*') {
				dp[slen][j] = true;
			} else {
				break;
			}
		}
		if (slen > 0 && elen > 0) {
			if ((e[elen - 1] == '.' || s[slen - 1] == e[elen - 1])) {
				dp[slen - 1][elen - 1] = true;
			}
		}
		return dp;
	}

	public static void main(String[] args) {
		String str = "abcccdefg";
		String exp = "ab.*d.*e.*";
		System.out.println(isMatch(str, exp));
		System.out.println(isMatchDP(str, exp));

	}

}

**子数组的最大异或和 **

数组异或和的定义:把数组中所有的数异或起来得到的值

给定一个整型数组 arr，其中可能有正、有负、有零，求其中子数组的最大异或和

【举例】

arr = {3} 数组只有1个数，所以只有一个子数组，就是这个数组本身，最大异或和为3

arr = {3, -28, -29, 2} 子数组有很多，但是{-28, -29}这个子数组的异或和为7，是所有子数组中最大的

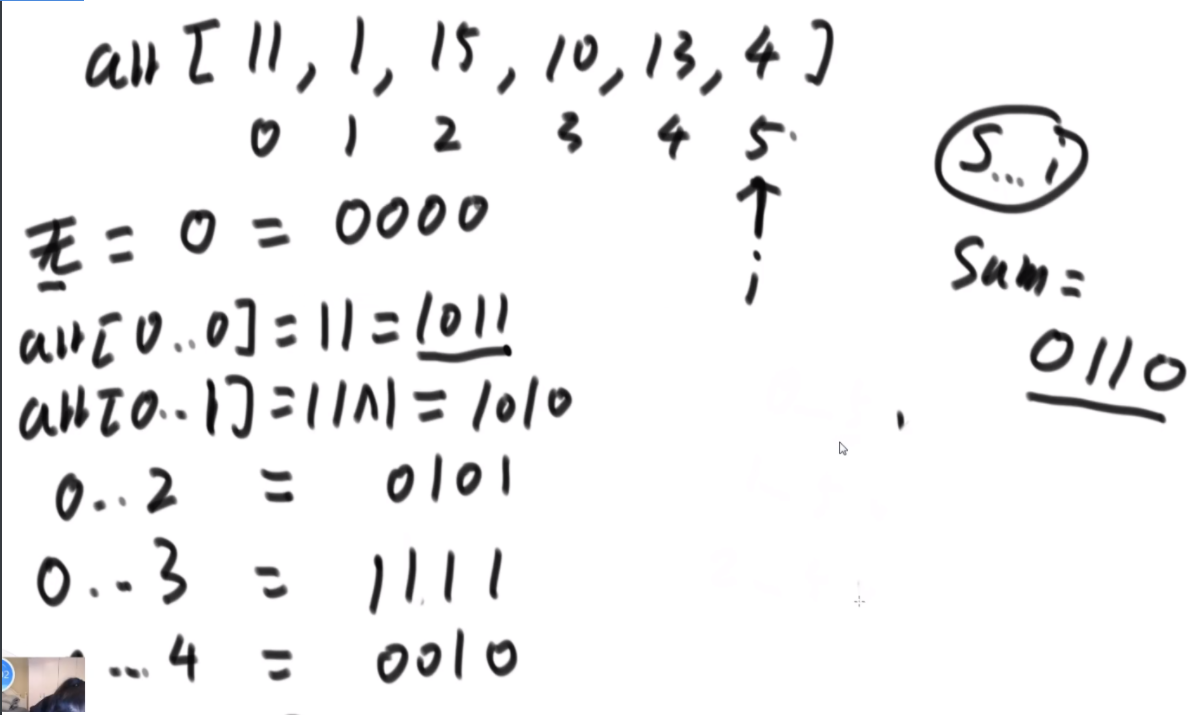
思路：最笨的思路是找每个以i位置为结尾的最大异或和，然后3层for循环，然后稍微好一点的是通过缓存数组记录一下，因为假如你现在有0-4位置所有的异或和信息，那么你现在想要3-5的，那你直接用0-4的异或上5再异或0-2的就能得到，因此可以少一层for循环。

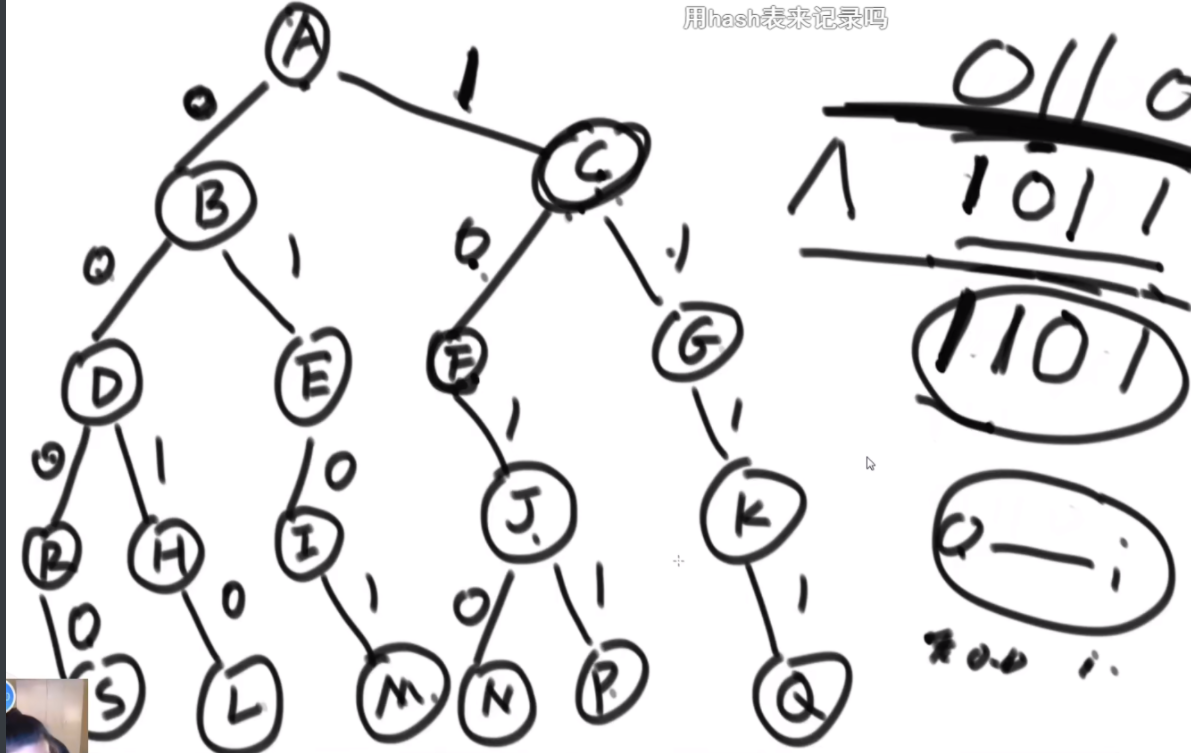
前缀树思路：这里用到了一个贪心策略，因为是异或和，那么从高位开始，让自己偏向于去异或让自己成为1的值，这样永远是最大的。然后遍历一遍就可以了。每次需要一个O(32)的时间复杂度去获取最佳路径，同时还要搞一个前缀树的实现，以及有符号数的第一位应当是找与自己一样的让这一位变成0，即正数。这个前缀树每个有32层，然后去看代码注释即可。

package class07;

public class Problem02_MaxEOR {

	public static class Node {
		public Node[] nexts = new Node[2]; //存放左右两个节点 0和1由数组位置表示
	}

	// 把所有前缀异或和，加入到NumTrie，并按照前缀树组织
	public static class NumTrie {
		public Node head = new Node();

		public void add(int num) {
			Node cur = head;
			for (int move = 31; move >= 0; move--) { // move：向右位移多少次
				int path = ((num >> move) & 1);
				cur.nexts[path] = cur.nexts[path] == null ? new Node() : cur.nexts[path];
				cur = cur.nexts[path];
			}
		}
		// num:32位有符号位  那么第一位是1的时候希望遇到1，这样异或后是0可以是正数
		// 如果是0的话希望是0，因此是正数
		// sum最希望遇到的路径，最大的异或结果 返回O(32)
		public int maxXor(int num) {
			Node cur = head;
			int res = 0; // 最后的结果(num^最优选择)所得到的值
			for (int move = 31; move >= 0; move--) {
				// 当前位如果是0，path就是整数0
				// 当前位如果是1，path就是整数1
				int path = (num >> move) & 1;// num是第move位置上的状态提取出来
				// sum该位的状态，最期待的路 如果是符号位，期待的是结果为1
				int best = move == 31 ? path : (path ^ 1);
				// best:最期待的路->实际走的路 如果最期待的路可以走，那就走，否则只能走向相反的路
				best = cur.nexts[best] != null ? best : (best ^ 1);
				// path num第move位的状态，best是根据path实际走的路
				res |= (path ^ best) << move;
				cur = cur.nexts[best];
			}
			return res;
		}

	}

	public static int maxXorSubarray(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		int eor = 0; //一个数都没有时，异或和为0
		NumTrie numTrie = new NumTrie();
		numTrie.add(0);
		for (int i = 0; i < arr.length; i++) {
			eor ^= arr[i]; // eor -> 0~i 异或和
			// numTrie装着所有：一个数也没有、0~0、0~1、0~2、0~i-1
			max = Math.max(max, numTrie.maxXor(eor));//maxXor函数帮你选出最大
			// 将这个eor加入
			numTrie.add(eor);
		}
		return max;
	}

	// for test
	public static int comparator(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < arr.length; i++) {
			int eor = 0;
			for (int j = i; j < arr.length; j++) {
				eor ^= arr[j];
				max = Math.max(max, eor);
			}
		}
		return max;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 30;
		int maxValue = 50;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			int res = maxXorSubarray(arr);
			int comp = comparator(arr);
			if (res != comp) {
				succeed = false;
				printArray(arr);
				System.out.println(res);
				System.out.println(comp);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}
}

能获得最高分数的打爆气球顺数

给定一个数组arr，代表一排有分数的气球。每打爆一个气球都能获得分数，假设打爆气 球 的分数为 X，获得分数的规则如下:

1)如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为L;如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为R。 获得分数为 LXR。

2)如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为L;如果被打爆气球的右边所有气球都已经被打爆。获得分数为 L*X。

3)如果被打爆气球的左边所有的气球都已经被打爆;如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 R;如果被打爆气球的右边所有气球都已经 被打爆。获得分数为 X*R。

4)如果被打爆气球的左边和右边所有的气球都已经被打爆。获得分数为 X。目标是打爆所有气球，获得每次打爆的分数。

通过选择打爆气球的顺序，可以得到不同总分，请返回能获得的最大分数。

【举例】

arr = {3,2,5}

如果先打爆3，获得32；再打爆2，获得25；最后打爆5，获得5；最后总分21

如果先打爆3，获得32;再打爆5，获得25；最后打爆2，获得2；最后总分18

如果先打爆2，获得325；再打爆3，获得3*5；最后打爆5，获得5；最后总分50

如果先打爆2，获得325；再打爆5，获得3*5；最后打爆3，获得3；最后总分48

如果先打爆5，获得25；再打爆3，获得32；最后打爆2，获得2；最后总分18

如果先打爆5，获得25;再打爆2，获得32；最后打爆3，获得3；最后总分19

返回能获得的最大分数为50

思路：由于选择遍历每个位置最先打爆需要传入左右两侧最近的没打爆气球，因此这样的是4维的，舍弃这个思路。选择新的尝试，去搞最晚被打爆，这样那么可以获得左右两侧的值，然后递归，2维的正方形。

package class07;

public class Problem03_BurstBalloons {

	public static int maxCoins1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0];
		}
		int N = arr.length;
		int[] help = new int[N + 2];
		help[0] = 1;
		help[N + 1] = 1;
		// 3,2,5
		// 0 1 2
		// 1 3 2 5 1
		// 0 1 2 3 4
		// f(1,3) 加两个1 防止越界
		for (int i = 0; i < N; i++) {
			help[i + 1] = arr[i];
		}
		return process(help, 1, N);
	}

	// 打爆arr[L..R]范围上的所有气球，返回最大的分数
	// 假设arr[L-1]和arr[R+1]一定没有被打爆 
	// 尝试方式：每一个位置的气球都最后打爆
	// 这种尝试是因为，假设先打爆哪个，需要传入左右两边最近的没被打爆的气球，因此是4维的，因此换一种思路。
	public static int process(int[] arr, int L, int R) {
		if (L == R) {// 如果arr[L..R]范围上只有一个气球，直接打爆即可
			return arr[L - 1] * arr[L] * arr[R + 1];
		}
		// 最后打爆arr[L]的方案，和最后打爆arr[R]的方案，先比较一下
		int max = Math.max(
				arr[L - 1] * arr[L] * arr[R + 1] + process(arr, L + 1, R),
				arr[L - 1] * arr[R] * arr[R + 1] + process(arr, L, R - 1));
		// 尝试中间位置的气球最后被打爆的每一种方案
		for (int i = L + 1; i < R; i++) {
			//遍历每个中间的气球  比较最大值
			max = Math.max(max,arr[L - 1] * arr[i] * arr[R + 1] + process(arr, L, i - 1)+ process(arr, i + 1, R));
		}
		return max;
	}

	public static int maxCoins2(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0];
		}
		int N = arr.length;
		int[] help = new int[N + 2];
		help[0] = 1;
		help[N + 1] = 1;
		for (int i = 0; i < N; i++) {
			help[i + 1] = arr[i];
		}
		int[][] dp = new int[N + 2][N + 2];
		for (int i = 1; i <= N; i++) {
			dp[i][i] = help[i - 1] * help[i] * help[i + 1];
			System.out.println(dp[i][i]);
		}
		for (int L = N; L >= 1; L--) {
			for (int R = L + 1; R <= N; R++) {
				// 求解dp[L][R]，表示help[L..R]上打爆所有气球的最大分数
				// 最后打爆help[L]的方案
				int finalL = help[L - 1] * help[L] * help[R + 1] + dp[L + 1][R];
				// 最后打爆help[R]的方案
				int finalR = help[L - 1] * help[R] * help[R + 1] + dp[L][R - 1];
				// 最后打爆help[L]的方案，和最后打爆help[R]的方案，先比较一下
				dp[L][R] = Math.max(finalL, finalR);
				// 尝试中间位置的气球最后被打爆的每一种方案
				for (int i = L + 1; i < R; i++) {
					dp[L][R] = Math.max(dp[L][R], help[L - 1] * help[i]
							* help[R + 1] + dp[L][i - 1] + dp[i + 1][R]);
				}
			}
		}
		return dp[1][N];
	}

	public static void main(String[] args) {
		int[] arr = { 4, 2, 3, 5, 1, 6 };
		System.out.println(maxCoins1(arr));
		System.out.println(maxCoins2(arr));
	}

}

汉诺塔游戏到第几步（不太会）

汉诺塔游戏的要求把所有的圆盘从左边都移到右边的柱子上，给定一个整型数组arr，其中只含有1、2和3，代表所有圆盘目前的状态，1代表左柱，2代表中柱，3代表右柱，arr[i]的值代表第i+1个圆盘的位置。比如，arr=[3,3,2,1]，代表第1个圆盘在右柱上、第2个圆盘在右柱上、第3个圆盘在中柱上、第4个圆盘在左柱上如果arr代表的状态是最优移动轨迹过程中出现的状态，返回arr这种状态是最优移动轨迹中的第几个状态；如果arr代表的状态不是最优移动轨迹过程中出现的状态，则返回-1。

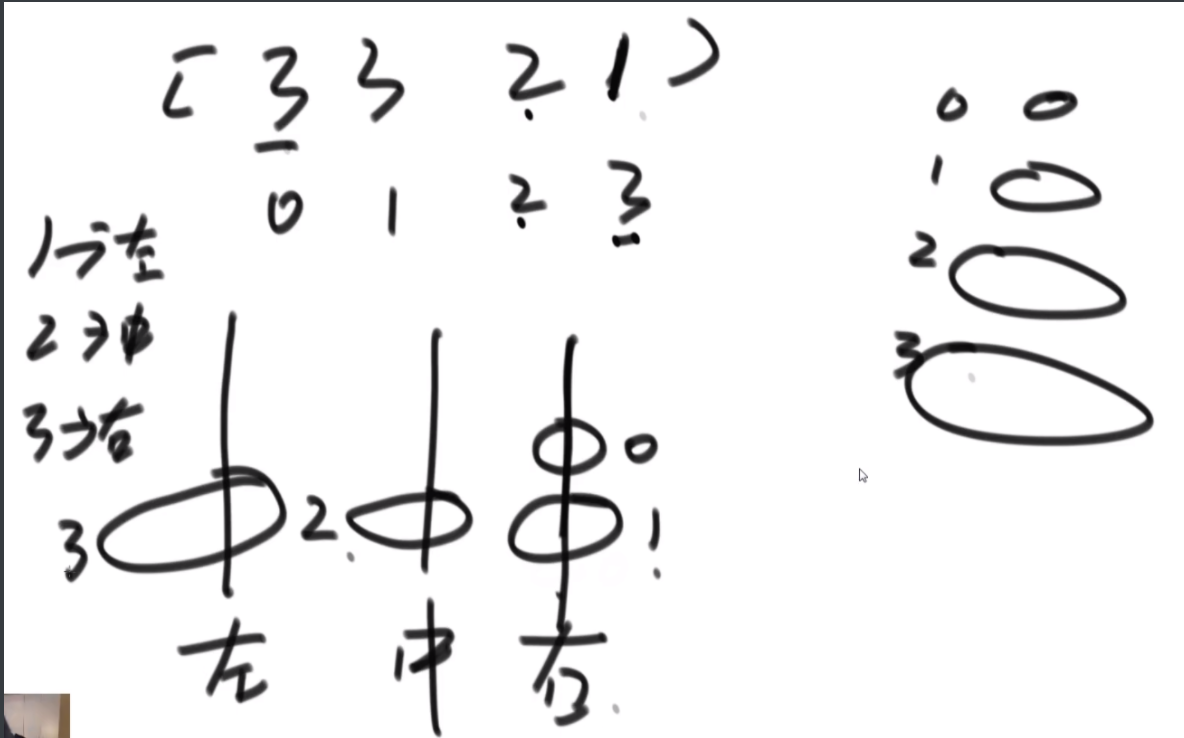
题目： 这个盘子是根据数组脚标越来越大，里面的值代表在哪个杆上。步数2^N-1。

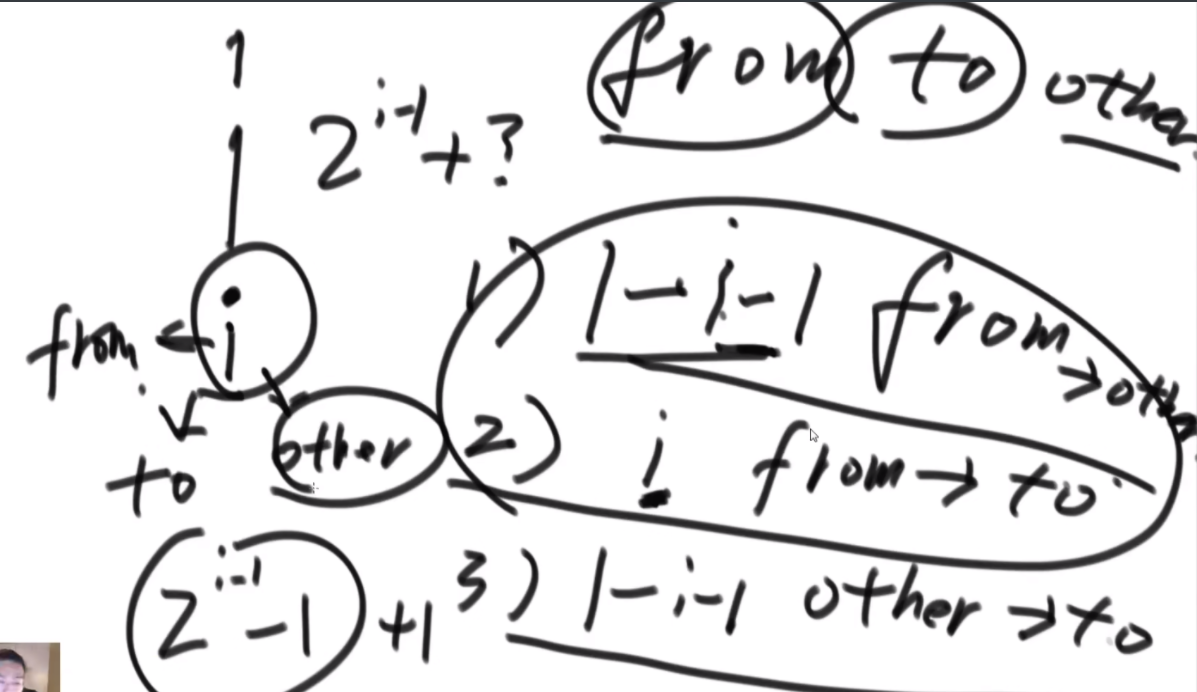
思路：假设i位置是最下面的一层，那么汉诺塔问题分为3步，第一步把1-i-1的盘子挪到other，第二步吧i挪到to，第三步吧1-i-1从other挪到to上，因此在这个过程中，第i个圆盘的位置只可能在from或者to上。

这个逻辑就是从最大的盘子开始看，你在to上嘛？如果在，那么说明你第三部完成了，如果没有，在from上，就去看第一步的完成程度，一直走到一个盘子发现没到呢或者在other上，说明此时是无效的步骤。（但是你挪动的过程中总会有盘子在other上啊，这种会直接判定-1，但是是合理的啊？好奇怪）啊 这个好像想明白了，这是因为，如果i在from上，那你的i-1应该是在第一步，从from到other，如果i在to上，那你的i-1应该在从other到to，这是通过控制每次传入的左中右的数字变化来控制的，你应该在哪。。。好难一个嗷

package class07;

public class Problem04_HanoiProblem {

	public static int step1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return -1;
		}
        // i是N 2是中间状态 other
		return process(arr, arr.length - 1, 1, 2, 3);
	}
	
    // 目标是：把arr[0-i]的圆盘，从from全部挪到to上
	// 返回，根据arr中的状态arr[0..i]，它是最优解的第几步？
    // O(N) 因为两个if只有可能走一个，而且从N开始，每次-1
	public static int process(int[] arr, int i, int from, int mid, int to) {
		if (i == -1) {
			return 0;
		}
		if (arr[i] != from && arr[i] != to) {
			return -1;
		}
		// arr[i] from or to 
		if (arr[i] == from) { // 第一大步没走完 0..i-1 from -> other to
			return process(arr, i - 1, from, to, mid);
		} else { // arr[i] == to
			int rest = process(arr, i - 1, mid, from, to); // 第三大步的完成的程度
			if (rest == -1) {
				return -1;
			}
			return (1 << i) + rest;
		}
	}

	public static int step2(int[] arr) {
		if (arr == null || arr.length == 0) {
			return -1;
		}
		int from = 1;
		int mid = 2;
		int to = 3;
		int i = arr.length - 1;
		int res = 0;
		int tmp = 0;
		while (i >= 0) {
			if (arr[i] != from && arr[i] != to) {
				return -1;
			}
			if (arr[i] == to) {
				res += 1 << i;
				tmp = from;
				from = mid;
			} else {
				tmp = to;
				to = mid;
			}
			mid = tmp;
			i--;
		}
		return res;
	}

	public static void main(String[] args) {

		int[] arr = { 3, 3, 2, 1 };
		System.out.println(step1(arr));
		System.out.println(step2(arr));

	}
}

p35:

无序数组中，最小的第K个数

在一个无序数组中，求最小的第K个数

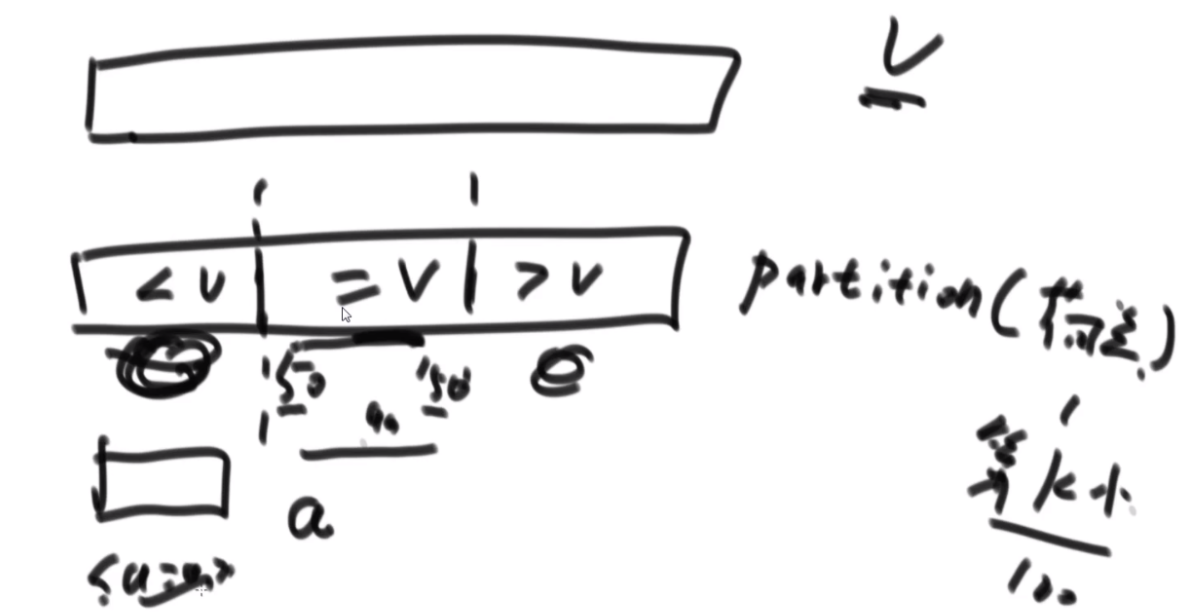
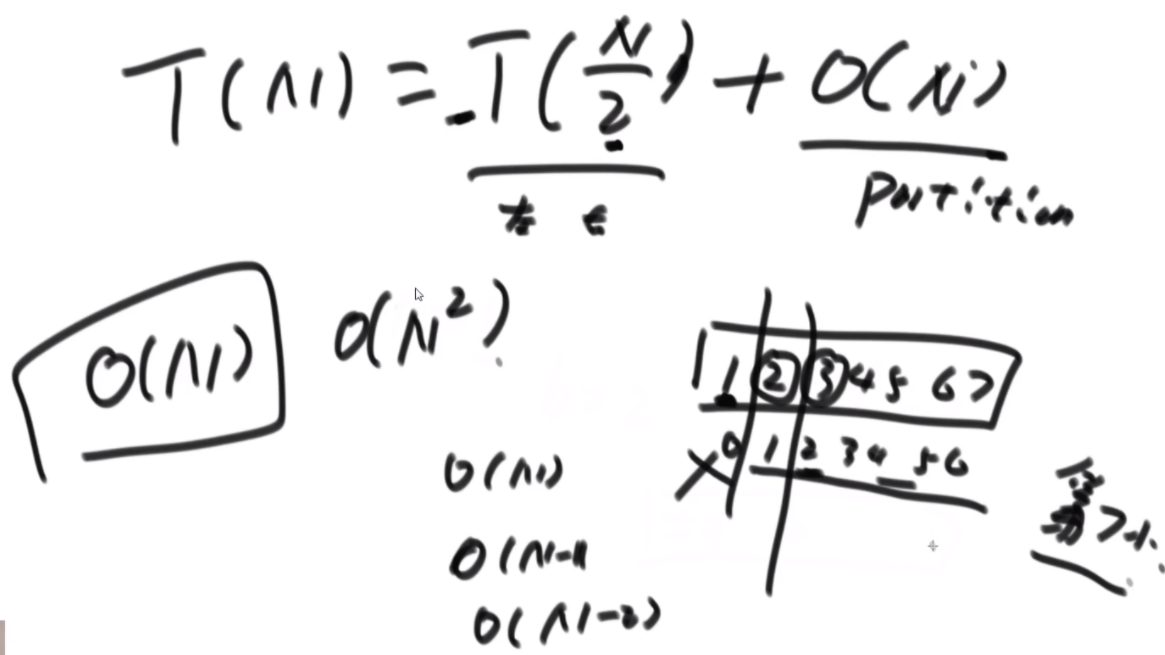
普通方法：大致方法就是类似于荷兰国旗（快排的一步），首先随机挑一个数V，然后小于它的排左边，大于它的排右边，接下来只需要排其中的一半就行了，如果V左边不够K个，那么去右边继续排，如果大于K个，去左边排。根据P3的Master公式，最好的情况下是T（N）的公式，为O(N)，最差的话是顺序求最大的情况，为O(N²).

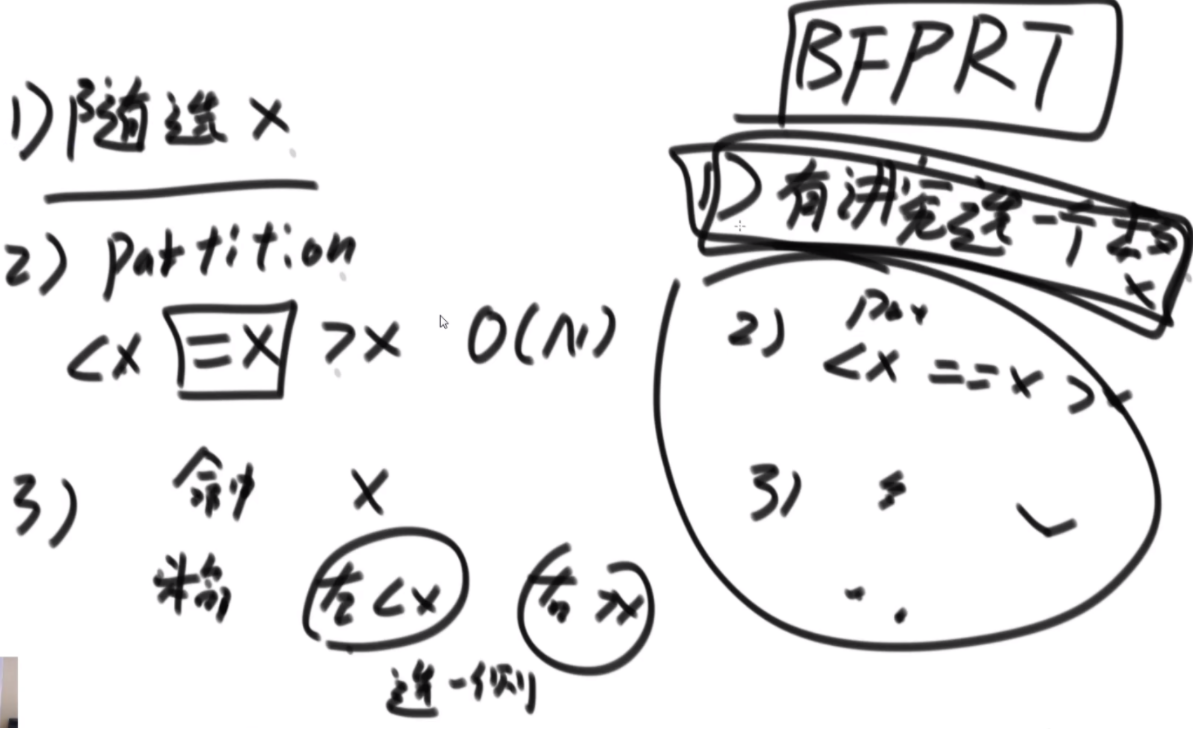
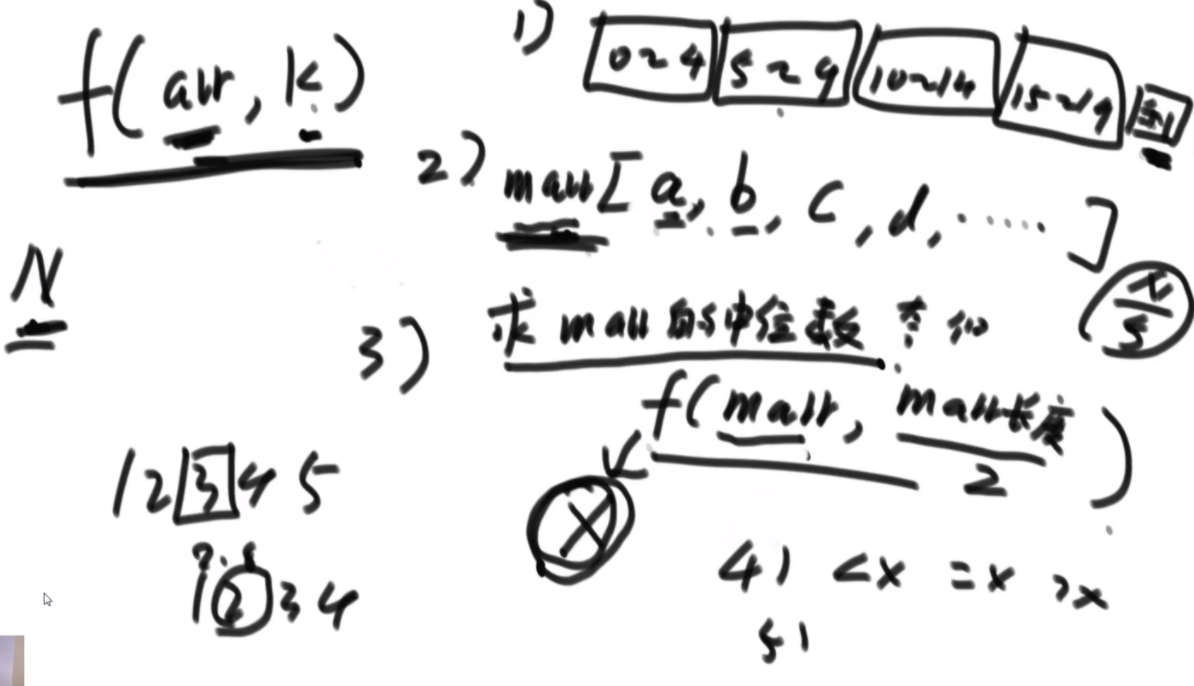
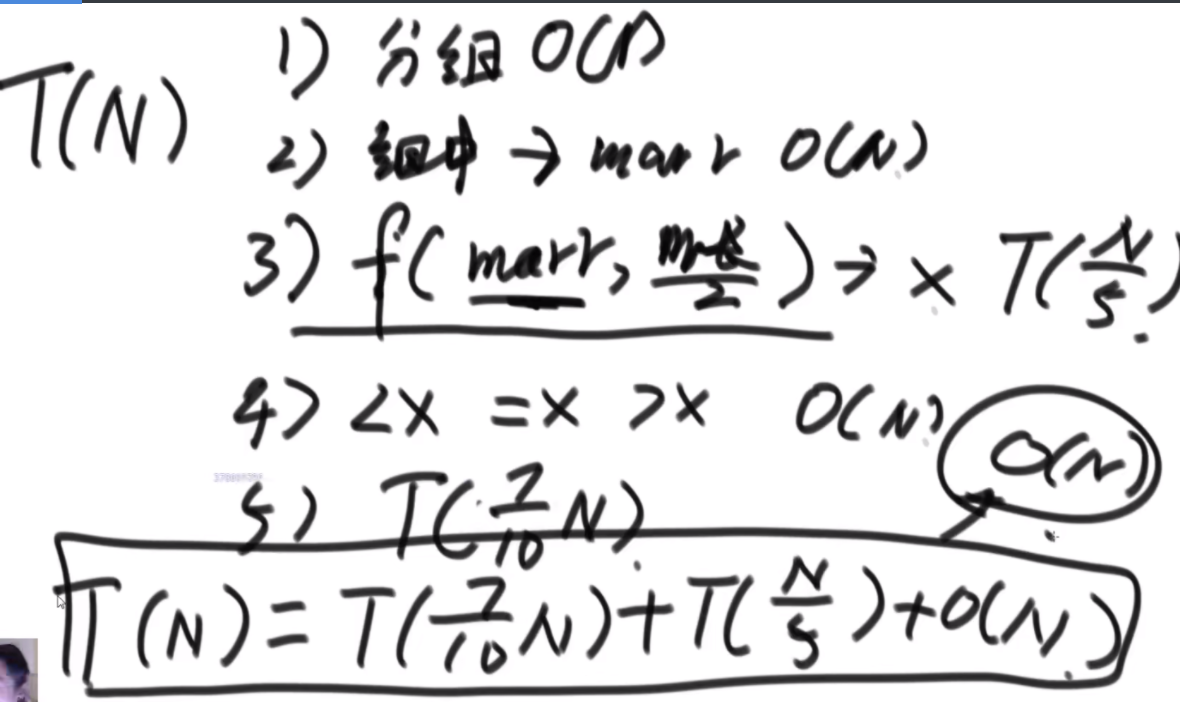
BFPRT(五友方法)：第二三部分直接一样，只在第一部分选择数字的时候很讲究。第一步分为5个组，每个组一样的大小O(1)。第二步每个组中挑选中位数，这些中位数拿出来组成了marr，这个过程是O(N)的。第三步，求marr的中位数，O(N/5)然后通过f函数找到总体的上中位数x，f函数中输入marr以及marr的长度/2.相当于去求解marr中第m长/2大的数字，递归的去获取这个中位数，x。第四步和第五步就是一样的。

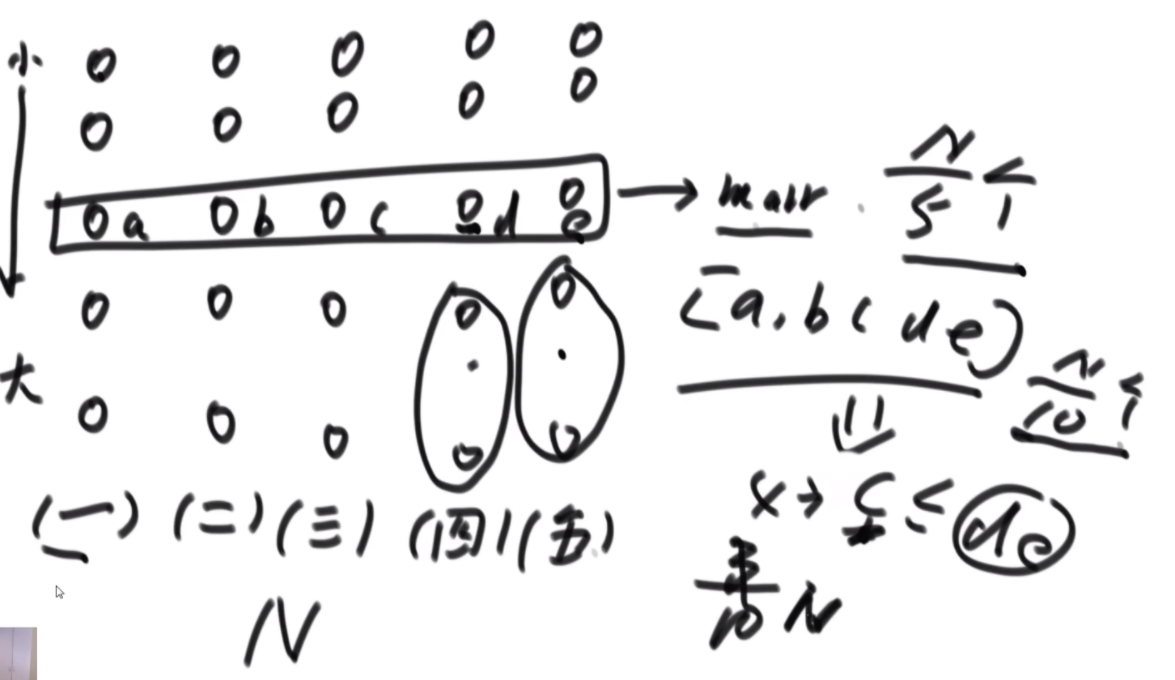
分析：为什么上面的情况差，因为<x的最多有多少个等价于N->=x至少有多少个，这个数随机挑选有可能最差，最差情况就是x是这个数组中最大的，<x的个数为N。然后讲这个BFPRT为什么好：因为假设c是marr里的中位数，因为c是从一个数组中选出来的，这个数组的大小是N/5，又因为c是中位数，所以至少有N/10的数比c大，而d和e大于c，因此至少有十分之三N的数大于c.那么小于c的最多有十分之七N，左侧规模固定住了。

由此可得右下角的表达式，最终结果为O(N)。

package class04;

public class Problem06_BFPRT {

	public static int[] getMinKNumsByBFPRT(int[] arr, int k) {
		if (k < 1 || k > arr.length) {
			return arr;
		}
		int minKth = getMinKthByBFPRT(arr, k);
		int[] res = new int[k];
		int index = 0;
		for (int i = 0; i != arr.length; i++) {
			if (arr[i] < minKth) {
				res[index++] = arr[i];
			}
		}
		for (; index != res.length; index++) {
			res[index] = minKth;
		}
		return res;
	}

	public static int getMinKthByBFPRT(int[] arr, int K) {
		int[] copyArr = copyArray(arr);
		return select(copyArr, 0, copyArr.length - 1, K - 1);
	}

	public static int[] copyArray(int[] arr) {
		int[] res = new int[arr.length];
		for (int i = 0; i != res.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	//在arr[begin..end]范围上，求如果排序的话，i位置的数是谁，返回
	//i一定在begin~end范围上
	public static int select(int[] arr, int begin, int end, int i) {
		if (begin == end) {
			return arr[begin];
		}
		// 前三步 分组+组内排序+组成newarr+选出newarr的上中位数 pivot
		int pivot = medianOfMedians(arr, begin, end);
		// partition过程 根据pivot做划分值  <p ==p <p 返回等于区域的左边界和右边界
		// pivotRange[0] 等于区域的左边界
		// pivotRange[1] 等于区域的右边界
		int[] pivotRange = partition(arr, begin, end, pivot);
		if (i >= pivotRange[0] && i <= pivotRange[1]) {
			return arr[i];
		} else if (i < pivotRange[0]) {
			return select(arr, begin, pivotRange[0] - 1, i);
		} else {
			return select(arr, pivotRange[1] + 1, end, i);
		}
	}

	public static int medianOfMedians(int[] arr, int begin, int end) {
		int num = end - begin + 1;
		int offset = num % 5 == 0 ? 0 : 1;
		int[] mArr = new int[num / 5 + offset];
		for (int i = 0; i < mArr.length; i++) {
			int beginI = begin + i * 5;
			int endI = beginI + 4;
			mArr[i] = getMedian(arr, beginI, Math.min(end, endI));
		}
		// 子函数中调用了大函数
		return select(mArr, 0, mArr.length - 1, mArr.length / 2);
	}

	public static int[] partition(int[] arr, int begin, int end, int pivotValue) {
		int small = begin - 1;
		int cur = begin;
		int big = end + 1;
		while (cur != big) {
			if (arr[cur] < pivotValue) {
				swap(arr, ++small, cur++);
			} else if (arr[cur] > pivotValue) {
				swap(arr, cur, --big);
			} else {
				cur++;
			}
		}
		int[] range = new int[2];
		range[0] = small + 1;
		range[1] = big - 1;
		return range;
	}

	public static int getMedian(int[] arr, int begin, int end) {
		insertionSort(arr, begin, end);
		int sum = end + begin;
		int mid = (sum / 2) + (sum % 2);
		return arr[mid];
	}

	public static void insertionSort(int[] arr, int begin, int end) {
		for (int i = begin + 1; i != end + 1; i++) {
			for (int j = i; j != begin; j--) {
				if (arr[j - 1] > arr[j]) {
					swap(arr, j - 1, j);
				} else {
					break;
				}
			}
		}
	}

	public static void swap(int[] arr, int index1, int index2) {
		int tmp = arr[index1];
		arr[index1] = arr[index2];
		arr[index2] = tmp;
	}

	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int[] arr = { 6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9 };
		printArray(getMinKNumsByBFPRT(arr, 10));

	}

}

给定一个正数，求裂开的方法数（斜率优化）

给定一个正数1，裂开的方法有一种，(1)

给定一个正数2，裂开的方法有两种，(1和1)、(2)

给定一个正数3，裂开的方法有三种，(1、1、1)、(1、2)、(3)

给定一个正数4，裂开的方法有五种，(1、1、1、1)、(1、1、2)、(1、3)、（2、2）、 （4）

给定一个正数n，求裂开的方法数。

动态规划优化状态依赖的技巧

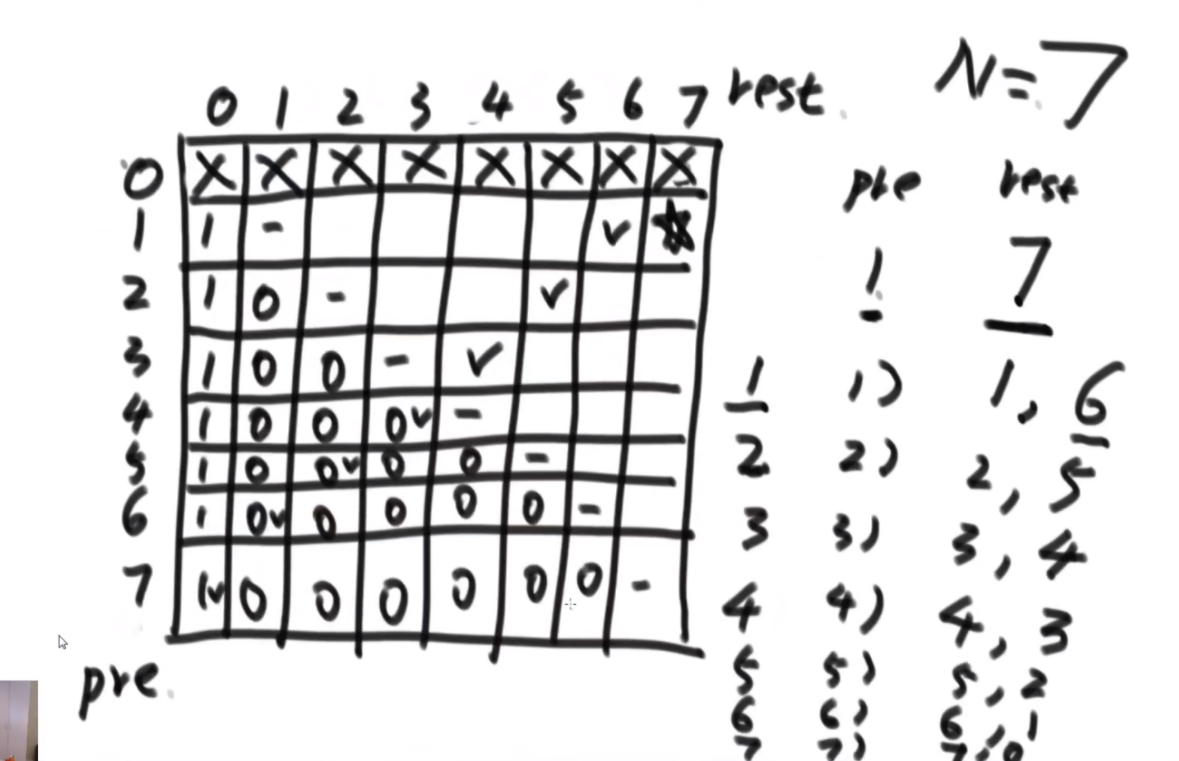
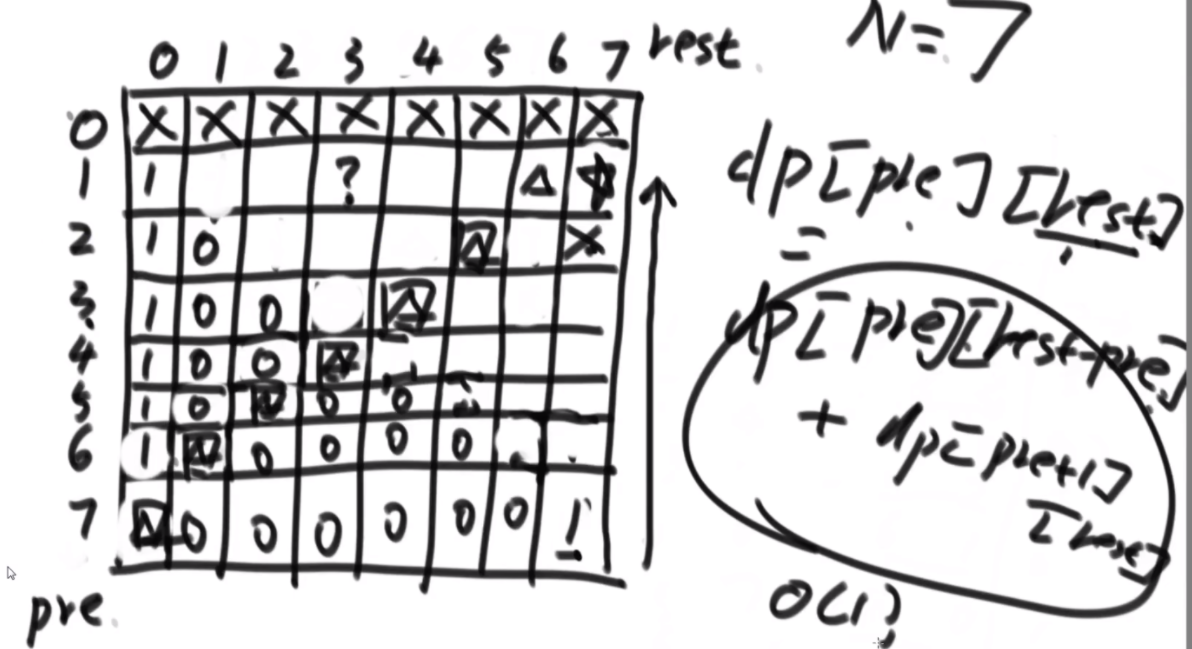
思路：首先是定义一个pre代表前一个数，然后定义一个rest是剩下来可以用的值，然后for循环+1去遍历递归。然后第一个图是记忆化搜索，第二个图是斜率优化，让递归行为消失。

package class05;

public class Problem02_SplitNumer {

	public static int ways1(int n) {
		if (n < 1) {
			return 0;
		}
		return process(1, n);
	}

	// pre 裂开的前一个部分
	// rest 还剩多少值，需要去裂开，要求裂出来的第一部分不要比pre小
	// 返回裂开的方法数
	public static int process(int pre, int rest) {
		if (rest == 0) {
			return 1; // 之前裂开的方案，构成了1种有效的方法，就是我的任务完成啦
		}
		if (pre > rest) {
			return 0;
		}
		int ways = 0;
		for (int i = pre; i <= rest; i++) { // i : rest第一个裂开的部分，值是多少
			ways += process(i, rest - i);
		}
		return ways;
	}
	//记忆化搜索
	public static int ways2(int n) {
		if (n < 1) {
			return 0;
		}
		int[][] dp = new int[n + 1][n + 1];
		for (int pre = 1; pre < dp.length; pre++) {
			dp[pre][0] = 1;
		}
		for (int pre = n; pre > 0; pre--) {
			for (int rest = pre; rest <= n; rest++) {
				for (int i = pre; i <= rest; i++) {
					dp[pre][rest] += dp[i][rest - i];
				}
			}
		}
		return dp[1][n];
	}
	//斜率优化
	public static int ways3(int n) {
		if (n < 1) {
			return 0;
		}
		int[][] dp = new int[n + 1][n + 1];
		for (int pre = 1; pre < dp.length; pre++) {
			dp[pre][0] = 1;
		}
		for (int pre = 1; pre < dp.length; pre++) {
			dp[pre][pre] = 1;
		}
		for (int pre = n - 1; pre > 0; pre--) {
			for (int rest = pre + 1; rest <= n; rest++) {
				dp[pre][rest] = dp[pre + 1][rest] + dp[pre][rest - pre];
			}
		}
		return dp[1][n];
	}

	public static void main(String[] args) {
		int n = 20;
		System.out.println(ways1(n));
		System.out.println(ways2(n));
		System.out.println(ways3(n));
	}

}

搜索二叉树最大拓扑结构的大小

给定一棵二叉树的头节点head，已知所有节点的值都不一样，返回其中最大的且符合搜索二叉树条件的最大拓扑结构的大小。

拓扑结构：不是子树，只要能连起来的结构都算。

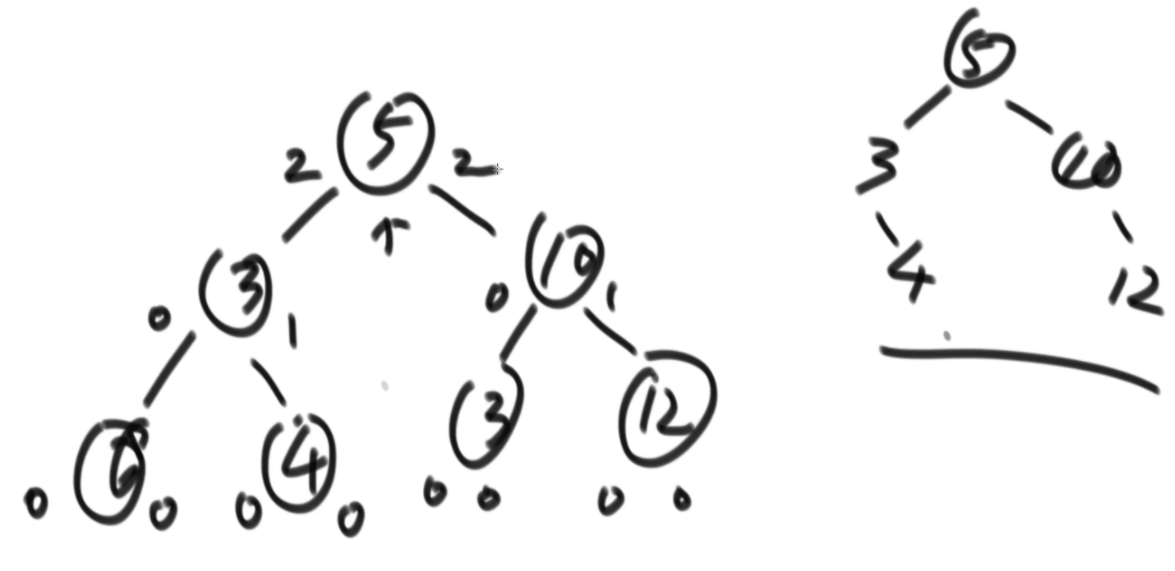
介绍拓扑结构：就是每个节点包含两个值，一个是它的左子树给它这个结构提供了多少个节点，一个是右子树提供了多少，每个节点对应的结构的起始位置是一致的，也就是说如果新的节点成为了头，需要下面去更新，更新成对应新的节点的结构。

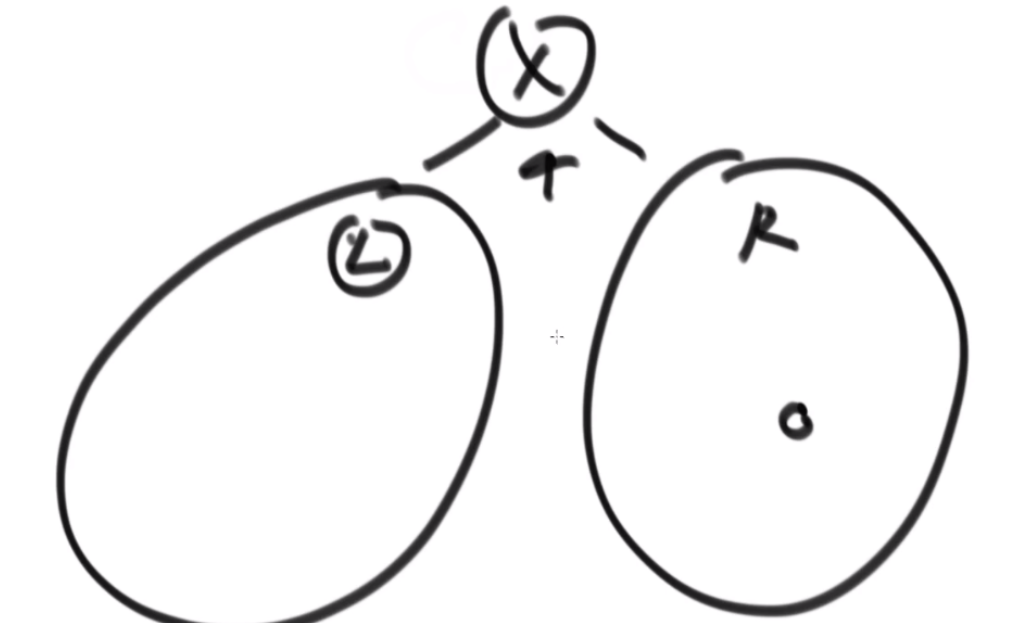
最佳思路：左侧代表其更新逻辑，通过加入x并且更新左右子树的每个节点的两个值来完成。右侧是一个具体的实例，当新加入一个节点18后，需要看两个地方，第一个是左子树的最右侧，因为如果这个节点小于18左子树的左子树一定都比18小，这些小于18的左子树节点会全部保留，因此直接不用动。继续往右下侧走，一直走到30发现大于18走不了了，因为30断了，那么30的左子树也就都不能要了，右子树更不用说。因此需要递归回去把每个节点的右侧减去30为头的树的节点个数。18右子树的最左侧也是同样的更新方法。

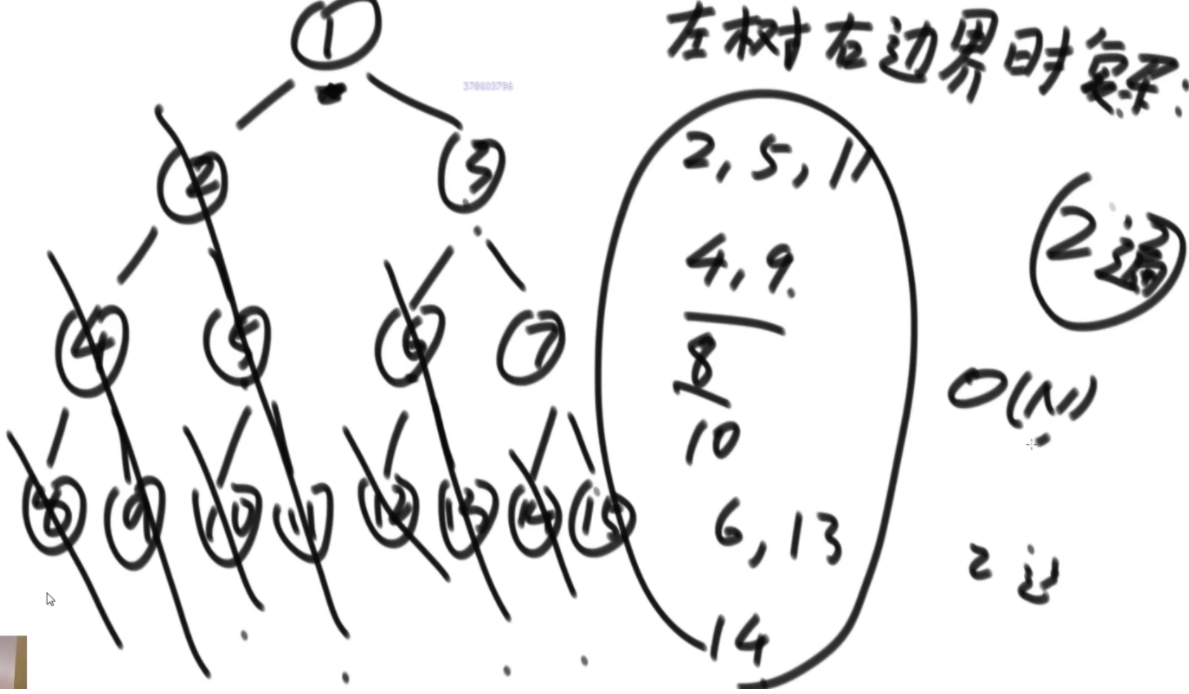
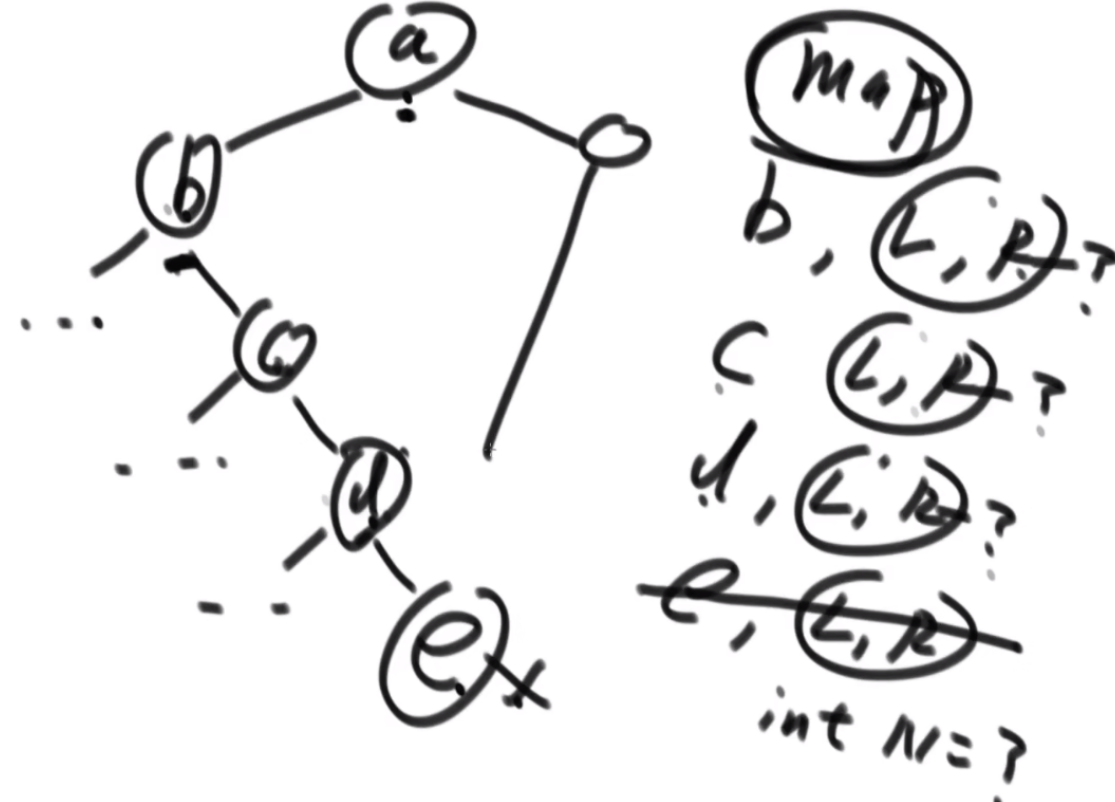
时间复杂度的计算：总体时间复杂度是O(N)，因为每个节点去遍历的节点并不会重复，而是一条条斜线，每个斜线过两遍，这个斜线总的节点数量是区域O(N)的，因此时间复杂度为O(N)。右侧图是具体的实现方法，是通过一个map保存。

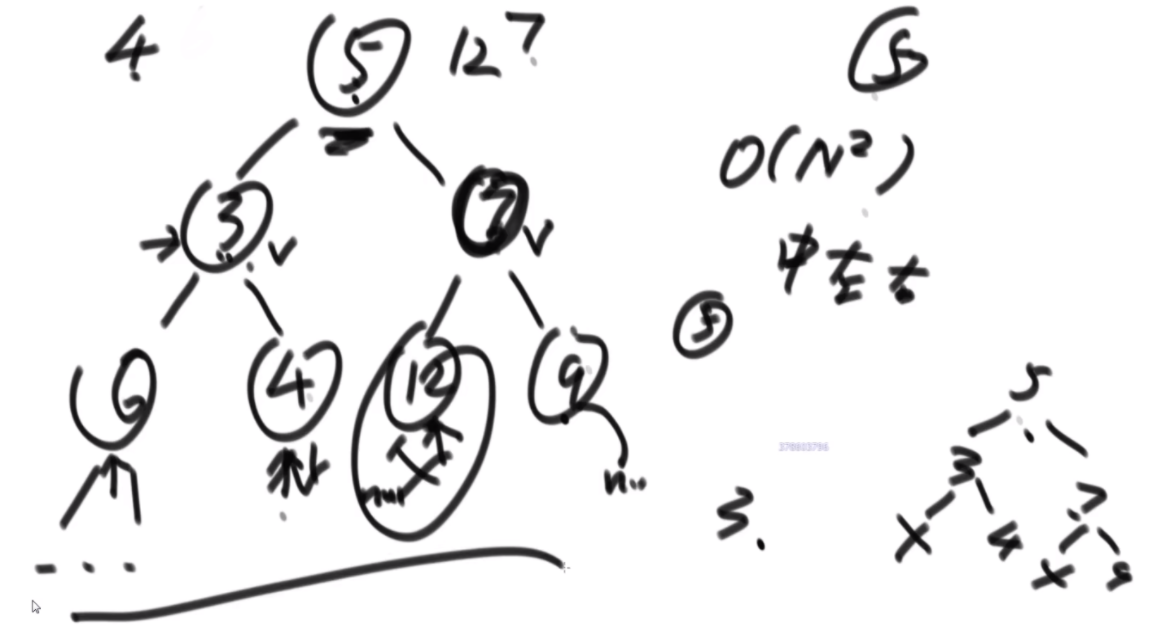
传统方法：每个节点去从头开始判断，能不能符合要求，过去的时候修改沿途的节点，因此时间复杂度是O(N²)

package class05;

import java.util.HashMap;
import java.util.Map;

public class Problem03_BiggestBSTTopologyInTree {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static int bstTopoSize1(Node head) {
		if (head == null) {
			return 0;
		}
		int max = maxTopo(head, head);
		max = Math.max(bstTopoSize1(head.left), max);
		max = Math.max(bstTopoSize1(head.right), max);
		return max;
	}

	public static int maxTopo(Node h, Node n) {
		if (h != null && n != null && isBSTNode(h, n, n.value)) {
			return maxTopo(h, n.left) + maxTopo(h, n.right) + 1;
		}
		return 0;
	}

	public static boolean isBSTNode(Node h, Node n, int value) {
		if (h == null) {
			return false;
		}
		if (h == n) {
			return true;
		}
		return isBSTNode(h.value > value ? h.left : h.right, n, value);
	}

	public static class Record {
		public int l;
		public int r;

		public Record(int left, int right) {
			this.l = left;
			t完美his.r = right;
		}
	}

	public static int bstTopoSize2(Node head) {
		Map<Node, Record> map = new HashMap<Node, Record>();
		return posOrder(head, map);
	}

	public static int posOrder(Node h, Map<Node, Record> map) {
		if (h == null) {
			return 0;
		}
		int ls = posOrder(h.left, map);
		int rs = posOrder(h.right, map);
		modifyMap(h.left, h.value, map, true);
		modifyMap(h.right, h.value, map, false);
		Record lr = map.get(h.left);
		Record rr = map.get(h.right);
		int lbst = lr == null ? 0 : lr.l + lr.r + 1;
		int rbst = rr == null ? 0 : rr.l + rr.r + 1;
		map.put(h, new Record(lbst, rbst));
		return Math.max(lbst + rbst + 1, Math.max(ls, rs));
	}

	public static int modifyMap(Node n, int v, Map<Node, Record> m, boolean s) {
		if (n == null || (!m.containsKey(n))) {
			return 0;
		}
		Record r = m.get(n);
		if ((s && n.value > v) || ((!s) && n.value < v)) {
			m.remove(n);
			return r.l + r.r + 1;
		} else {
			int minus = modifyMap(s ? n.right : n.left, v, m, s);
			if (s) {
				r.r = r.r - minus;
			} else {
				r.l = r.l - minus;
			}
			m.put(n, r);
			return minus;
		}
	}

	// for test -- print tree
	public static void printTree(Node head) {
		System.out.println("Binary Tree:");
		printInOrder(head, 0, "H", 17);
		System.out.println();
	}

	public static void printInOrder(Node head, int height, String to, int len) {
		if (head == null) {
			return;
		}
		printInOrder(head.right, height + 1, "v", len);
		String val = to + head.value + to;
		int lenM = val.length();
		int lenL = (len - lenM) / 2;
		int lenR = len - lenM - lenL;
		val = getSpace(lenL) + val + getSpace(lenR);
		System.out.println(getSpace(height * len) + val);
		printInOrder(head.left, height + 1, "^", len);
	}

	public static String getSpace(int num) {
		String space = " ";
		StringBuffer buf = new StringBuffer("");
		for (int i = 0; i < num; i++) {
			buf.append(space);
		}
		return buf.toString();
	}

	public static void main(String[] args) {
		Node head = new Node(6);
		head.left = new Node(1);
		head.left.left = new Node(0);
		head.left.right = new Node(3);
		head.right = new Node(12);
		head.right.left = new Node(10);
		head.right.left.left = new Node(4);
		head.right.left.left.left = new Node(2);
		head.right.left.left.right = new Node(5);
		head.right.left.right = new Node(14);
		head.right.left.right.left = new Node(11);
		head.right.left.right.right = new Node(15);
		head.right.right = new Node(13);
		head.right.right.left = new Node(20);
		head.right.right.right = new Node(16);
		printTree(head);

		System.out.println(bstTopoSize1(head));
		System.out.println(bstTopoSize2(head));

	}

}

完美洗牌问题

给定一个长度为偶数的数组arr，长度记为2*N。前N个为左部分，后N个为右部分。arr就可以表示为{L1,L2,..,Ln,R1,R2,..,Rn}，

请将数组调整成{R1,L1,R2,L2,..,Rn,Ln}的样子。

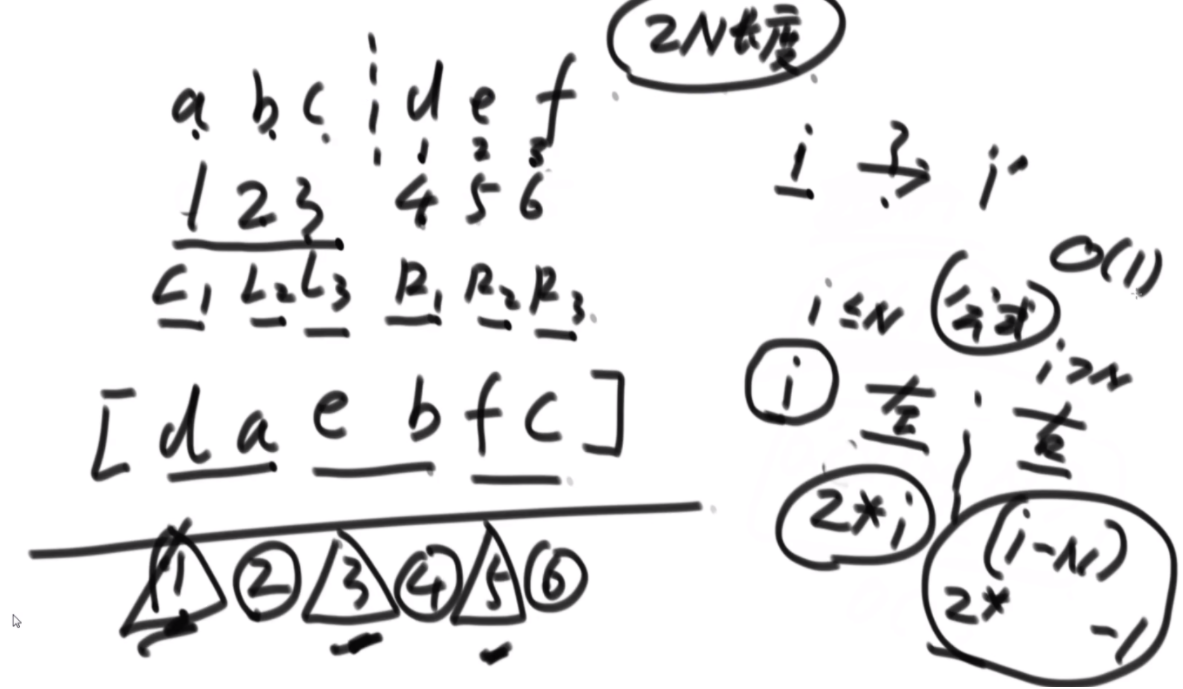
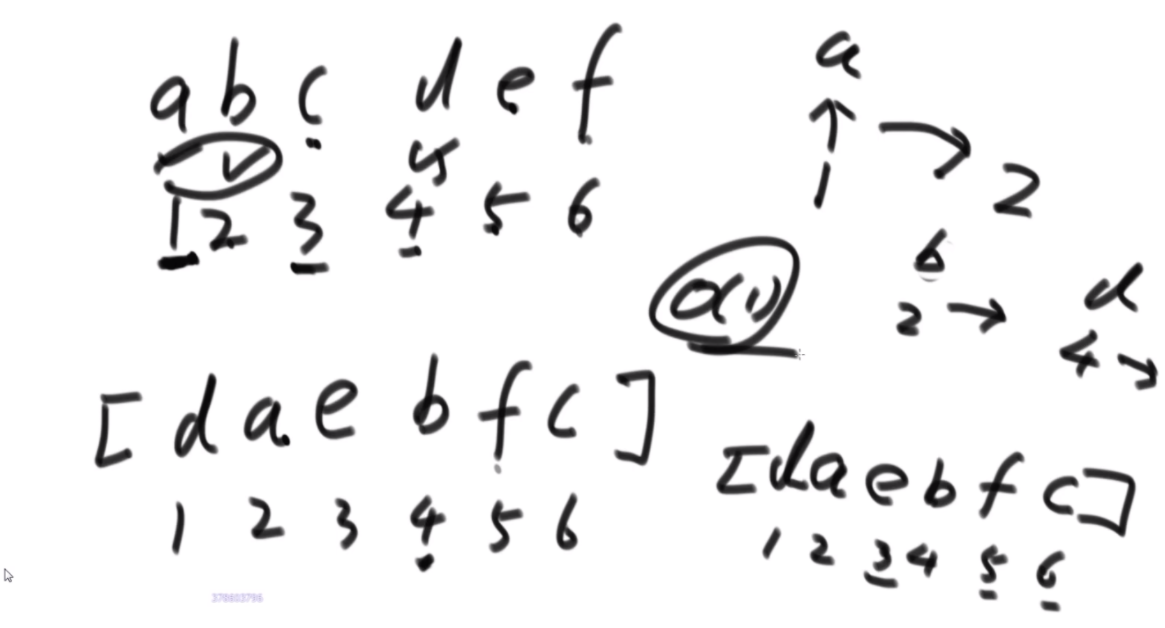
首先是问题的描述：由于是不让使用额外的空间，因此直接原地转换，想到的是坐标一直怼的方法，例如右图中，a通过公式找到自己坐标是2，2位置是b，b找到自己位置是4，这样就可以把4位置的d对出来找到d，d根据公式来到1，然后结束了就。会发现好像书上教的快排，这里的话偶数只有特殊位置的才能找到特定的环的入口，而6显然不是。

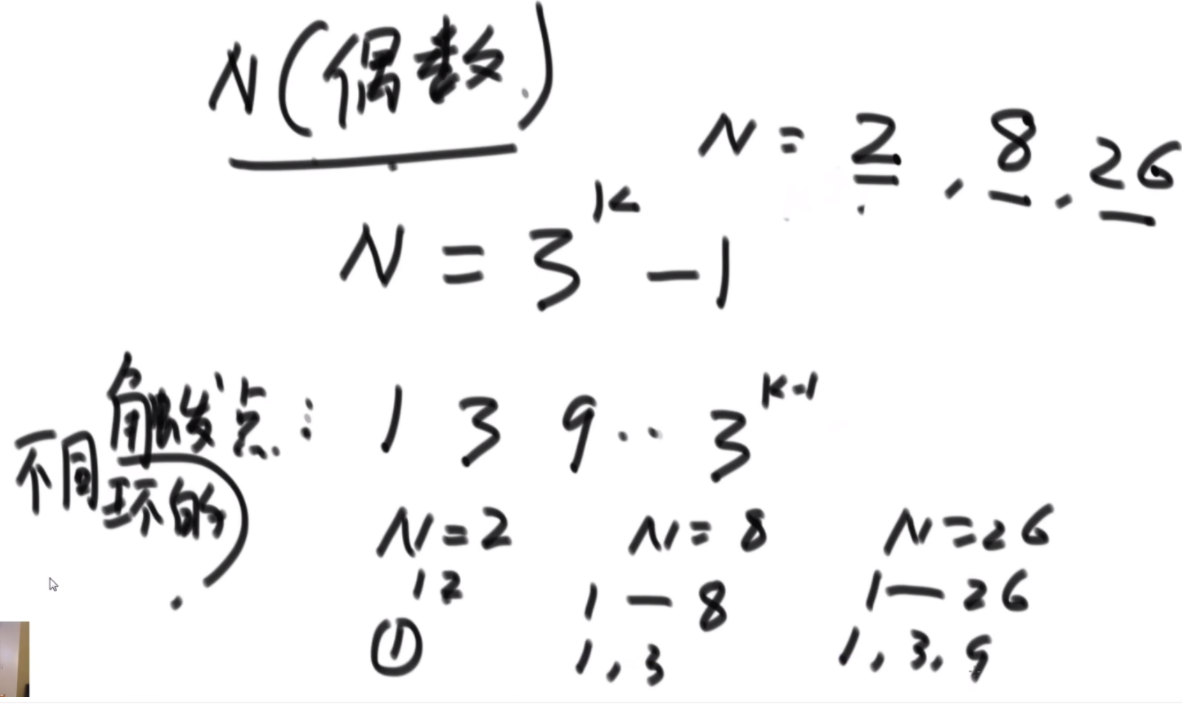
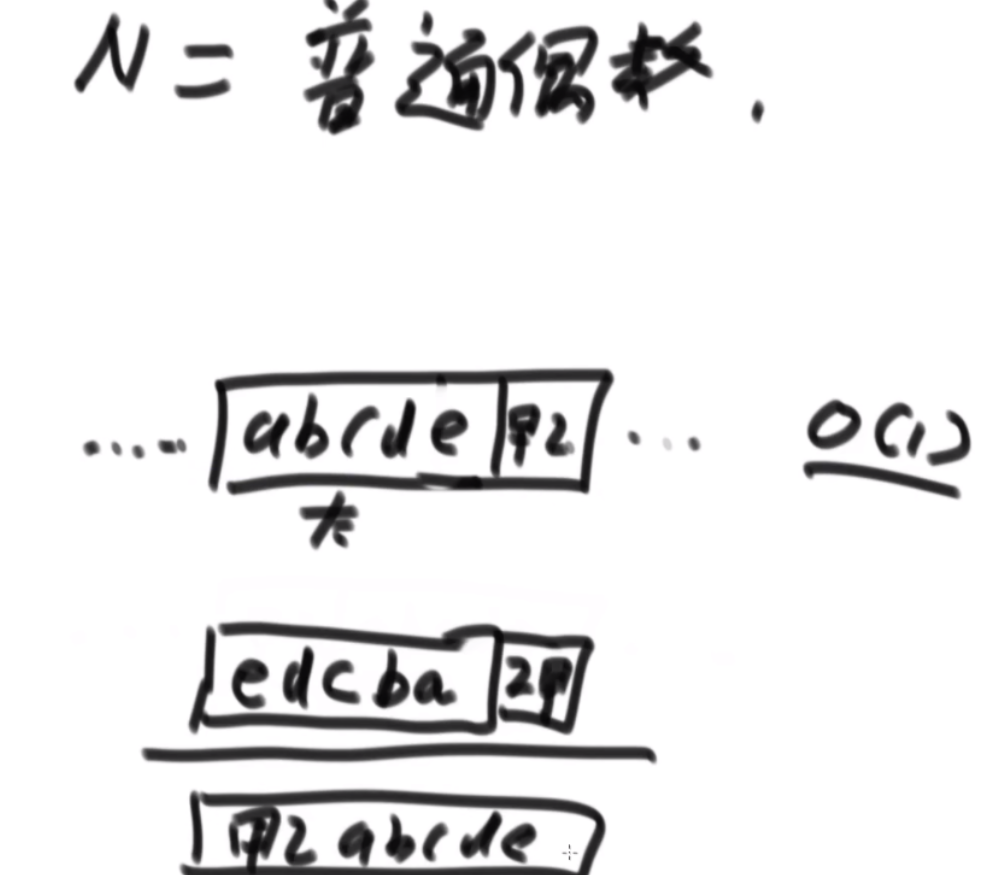
特定长度的环的入口：当N的长度为3^K-1的时候，这个偶数的长度可以找到固定的入口，比如长度为2的时候，入口为1；长度为8的时候，入口为1，3；长度为26的时候，入口为1，3，9.这样我们就可以处理特定长度的偶数数组了，而题目中的数组隐含条件就是都为偶数。这里看如何将右图中的甲乙换到前面呢，首先将abcde以c为轴逆序，然后将甲乙逆序，然后再将整体逆序，这样甲乙就到前面了，接下来会用到这个技巧。

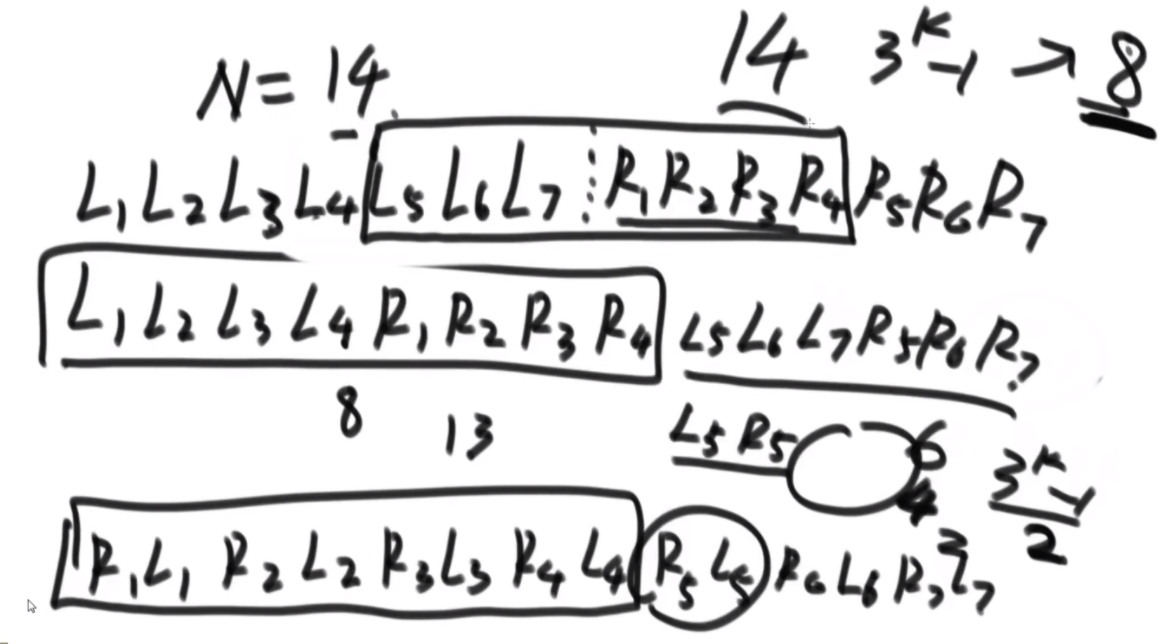
思路：假设长度为14，那么先找到3^K-1最接近14的数字是8，取这两个数组的前四个，这里需要把第二个数组的前四个的都置换到前面，先将L567逆序，然后逆序R1234，再整体逆序，就可以凑成一个8长度的，套用公式了。剩下的凑成3个2长度的完成。

package class05;

import java.util.Arrays;

public class Problem04_ShuffleProblem {

	// 数组的长度为len，调整前的位置是i，返回调整之后的位置
	// 下标不从0开始，从1开始
	public static int modifyIndex1(int i, int len) {
		if (i <= len / 2) {
			return 2 * i;
		} else {
			return 2 * (i - (len / 2)) - 1;
		}
	}

	// 数组的长度为len，调整前的位置是i，返回调整之后的位置
	// 下标不从0开始，从1开始
	public static int modifyIndex2(int i, int len) {
		return (2 * i) % (len + 1);
	}

	// 主函数
	// 数组必须不为空，且长度为偶数
	public static void shuffle(int[] arr) {
		if (arr != null && arr.length != 0 && (arr.length & 1) == 0) {
			shuffle(arr, 0, arr.length - 1);
		}
	}

	// 在arr[L..R]上做完美洗牌的调整
	public static void shuffle(int[] arr, int L, int R) {
		while (R - L + 1 > 0) { // 切成一块一块的解决，每一块的长度满足(3^k)-1
			int len = R - L + 1;
			int base = 3;
			int k = 1;
			// 计算小于等于len并且是离len最近的，满足(3^k)-1的数
			// 也就是找到最大的k，满足3^k <= len+1
			while (base <= (len + 1) / 3) {
				base *= 3;
				k++;
			}
			// 当前要解决长度为base-1的块，一半就是再除2
			int half = (base - 1) / 2;
			// [L..R]的中点位置
			int mid = (L + R) / 2;
			// 要旋转的左部分为[L+half...mid], 右部分为arr[mid+1..mid+half]
			// 注意在这里，arr下标是从0开始的
			rotate(arr, L + half, mid, mid + half);
			// 旋转完成后，从L开始算起，长度为base-1的部分进行下标连续推
			cycles(arr, L, base - 1, k);
			// 解决了前base-1的部分，剩下的部分继续处理
			L = L + base - 1;
		}
	}

	// 从start位置开始，往右len的长度这一段，做下标连续推
	// 出发位置依次为1,3,9...
	public static void cycles(int[] arr, int start, int len, int k) {
		// 找到每一个出发位置trigger，一共k个
		// 每一个trigger都进行下标连续推
		// 出发位置是从1开始算的，而数组下标是从0开始算的。
		for (int i = 0, trigger = 1; i < k; i++, trigger *= 3) {
			int preValue = arr[trigger + start - 1];
			int cur = modifyIndex2(trigger, len);
			while (cur != trigger) {
				int tmp = arr[cur + start - 1];
				arr[cur + start - 1] = preValue;
				preValue = tmp;
				cur = modifyIndex2(cur, len);
			}
			arr[cur + start - 1] = preValue;
		}
	}

	// [L..M]为左部分，[M+1..R]为右部分，左右两部分互换
	public static void rotate(int[] arr, int L, int M, int R) {
		reverse(arr, L, M);
		reverse(arr, M + 1, R);
		reverse(arr, L, R);
	}

	// [L..R]做逆序调整
	public static void reverse(int[] arr, int L, int R) {
		while (L < R) {
			int tmp = arr[L];
			arr[L++] = arr[R];
			arr[R--] = tmp;
		}
	}

	public static void wiggleSort(int[] arr) {
		if (arr == null || arr.length == 0) {
			return;
		}
		// 假设这个排序是额外空间复杂度O(1)的，当然系统提供的排序并不是，你可以自己实现一个堆排序
		Arrays.sort(arr);
		if ((arr.length & 1) == 1) {
			shuffle(arr, 1, arr.length - 1);
		} else {
			shuffle(arr, 0, arr.length - 1);
			for (int i = 0; i < arr.length; i += 2) {
				int tmp = arr[i];
				arr[i] = arr[i + 1];
				arr[i + 1] = tmp;
			}
		}
	}

	// for test
	public static boolean isValidWiggle(int[] arr) {
		for (int i = 1; i < arr.length; i++) {
			if ((i & 1) == 1 && arr[i] < arr[i - 1]) {
				return false;
			}
			if ((i & 1) == 0 && arr[i] > arr[i - 1]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static int[] generateArray() {
		int len = (int) (Math.random() * 10) * 2;
		int[] arr = new int[len];
		for (int i = 0; i < len; i++) {
			arr[i] = (int) (Math.random() * 100);
		}
		return arr;
	}

	public static void main(String[] args) {
		for (int i = 0; i < 5000000; i++) {
			int[] arr = generateArray();
			wiggleSort(arr);
			if (!isValidWiggle(arr)) {
				System.out.println("ooops!");
				printArray(arr);
				break;
			}
		}
	}

}

WaggleShuffle

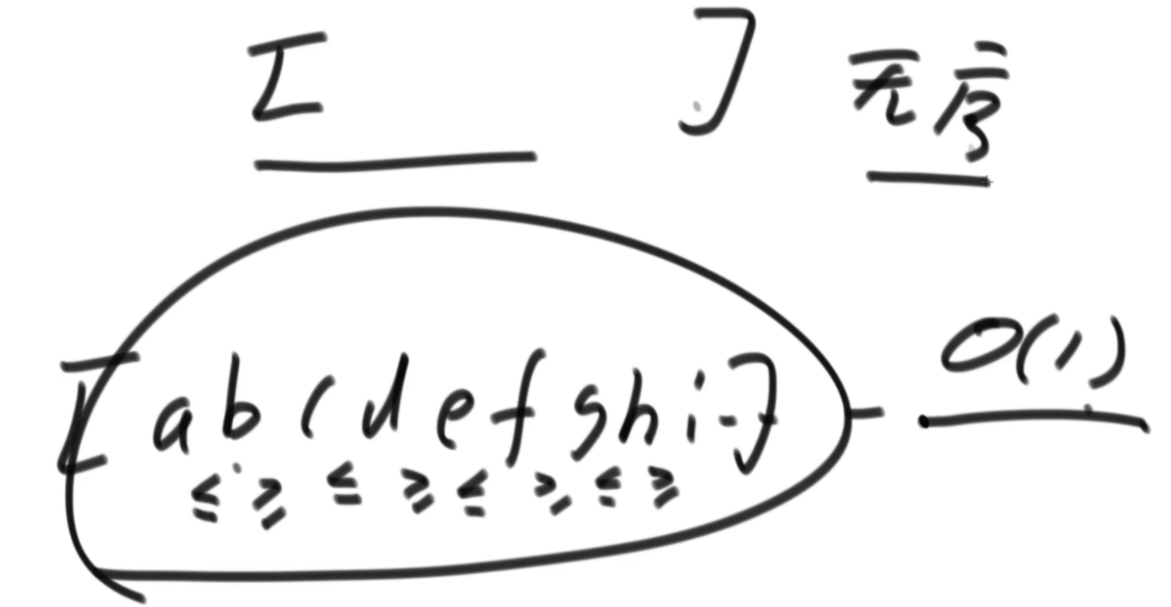
题目：一个无序的数组，要用O(1)的空间去把这个数组排序成a<=b>=c<=d>=e这种。

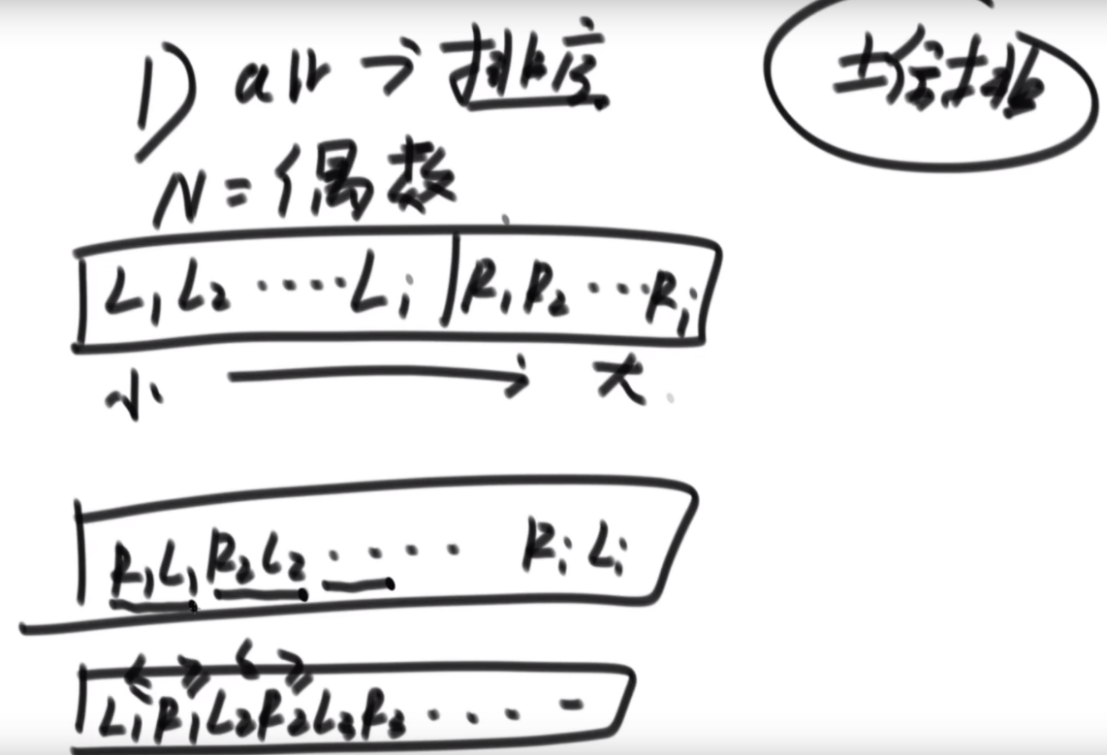
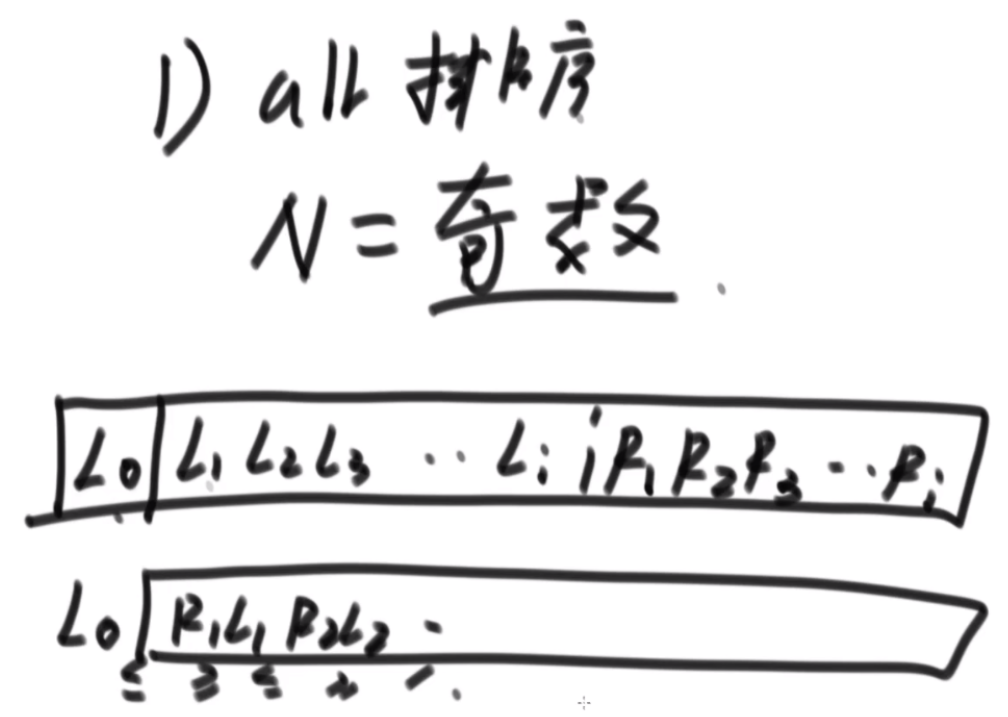
思路：首先用堆排序排序这个数组，因为堆排序不用额外空间，然后如果这个数组长度为偶数的话，直接弄就行，如果是奇数的话把第一个数留下就行了。

p34:

过河最少需要几条船

给定一个数组arr，长度为N且每个值都是正数，代表N个人的体重。再给定一个正数limit，代表一艘船的载重。以下是坐船规则，1）每艘船最多只能做两人；2）乘客的体重和不能超过limit。返回如果同时让这N个人过河最少需要几条船。

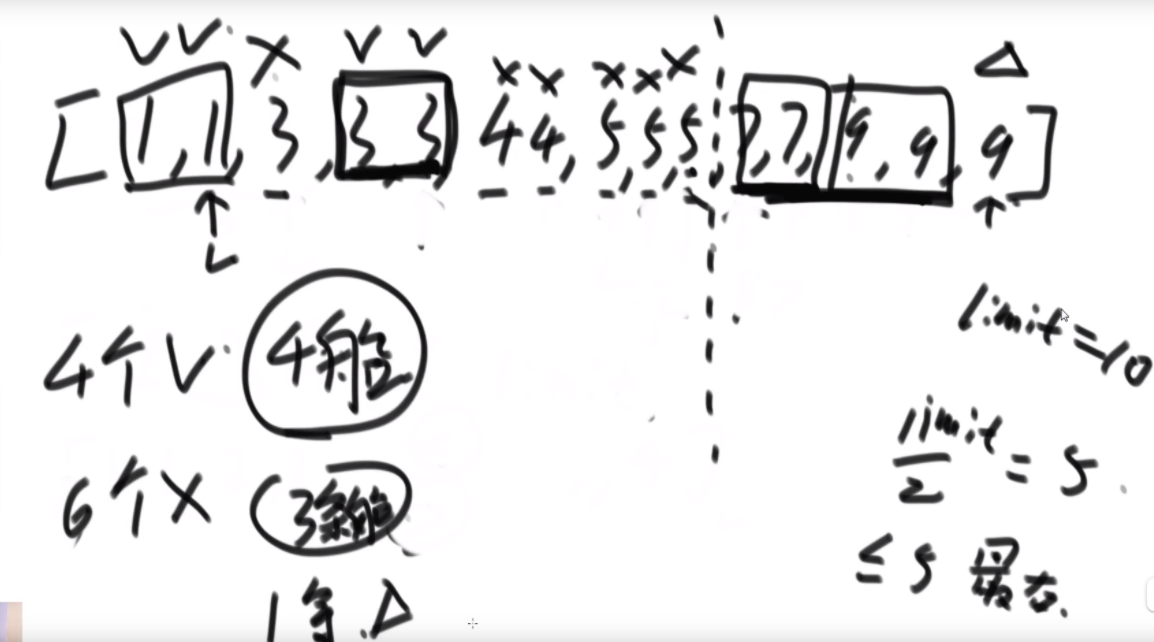
思路：这波是双指针但是从中间往两边走，先判断如果limit/2大于最大的，那么直接返回N/2，如果limit<最小的那么直接返回N，其余情况limit/2在中间位置，从中间开始看，往左数第一个能满足右边第一个的画对勾，其余画叉号，然后L和R往后走，右侧最后解决不了的画三角，最后的公式就是对号+叉号/2+三角。

package class04;

public class Problem01_MinBoat {

	// 请保证arr有序
	public static int minBoat(int[] arr, int weight) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int lessR = -1;
		for (int i = arr.length - 1; i >= 0; i--) {
			if (arr[i] <= (weight / 2)) {
				lessR = i;
				break;
			}
		}
		if (lessR == -1) {
			return arr.length;
		}
		int lessIndex = lessR;
		int moreIndex = lessR + 1;
		int lessUnused = 0; //X号
		while (lessIndex >= 0) {
			int solved = 0;
			while (moreIndex < arr.length
					&& arr[lessIndex] + arr[moreIndex] <= weight) {
				moreIndex++;
				solved++;
			}
			if (solved == 0) {
				lessUnused++;
				lessIndex--;
			} else {
				lessIndex = Math.max(-1, lessIndex - solved);
			}
		}
		int lessAll = lessR + 1; //左半区总个数 <= limit/2的区域
		int lessUsed = lessAll - lessUnused; //对号的数量
		int moreUnsolved = arr.length - lessR - 1 - lessUsed;// >limit/2的区域中，没搞定的数量
		return lessUsed + ((lessUnused + 1) >> 1) + moreUnsolved;//+1再除2可以向上取整
	}

	public static void main(String[] args) {
		int[] arr = { 1, 2, 2, 2, 2, 4, 4, 4, 4, 5 };
		int weight = 5;
		System.out.println(minBoat(arr, weight));
	}

}

最长的回文子序列(在范围上尝试的模型）

给定一个字符串str，求最长的回文子序列。注意区分子序列和子串的不同。遇到子序列的问题，大概率分为4种情况

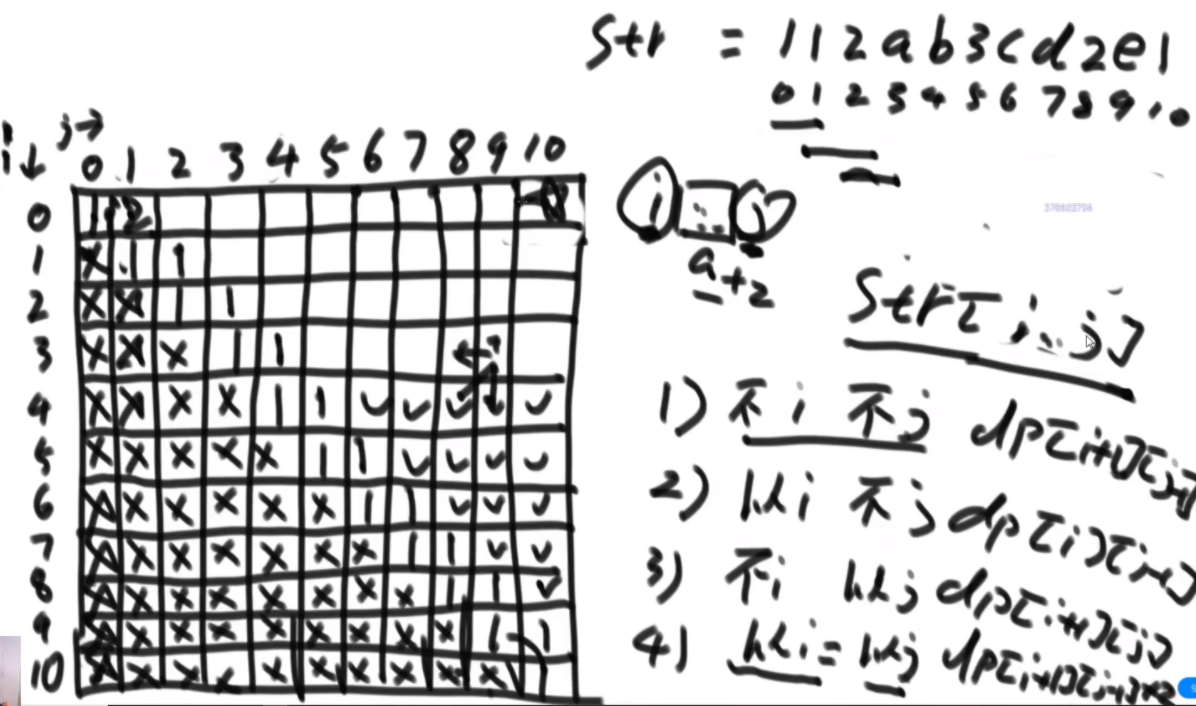
在范围上尝试的模型：str[i..j] string i位置到j位置上最长的回文子序列是多长，因为序列一定是i小于j的所以左下半区没意义，范围上的模型都是从对角线开始的，对角线的含义最简单。然后填第二个对角线，如果这俩字符相等，就是2，不相等就是1.

思路：首先分析可能性，这个子序列的结尾。

1. 如果不以i结尾，也不以j结尾，那么谁也不相关，那么dp【i+1】【j-1】
2. 如果以i结尾，不以j结尾，那么dp【i】【j-1】
3. 如果不以i结尾，以j结尾，那么dp【+1】【j】
4. 如果以i结尾，也以j结尾，那么dp【i+1】【j-1】+2 因为每个回文子序列的话要自己+2

package class04;

public class Problem02_PalindromeSubsequence {

	public static int maxLen1(String str) {
		if (str == null || str.length() == 0) {
			return 0;
		}
		char[] str1 = str.toCharArray();
		char[] str2 = reverse(str1);
		return lcse(str1, str2);
	}

	public static char[] reverse(char[] str) {
		char[] reverse = new char[str.length];
		for (int i = 0; i < reverse.length; i++) {
			reverse[i] = str[str.length - 1 - i];
		}
		return reverse;
	}

	public static int lcse(char[] str1, char[] str2) {
		int[][] dp = new int[str1.length][str2.length];
		dp[0][0] = str1[0] == str2[0] ? 1 : 0;
		for (int i = 1; i < str1.length; i++) {
			dp[i][0] = Math.max(dp[i - 1][0], str1[i] == str2[0] ? 1 : 0);
		}
		for (int j = 1; j < str2.length; j++) {
			dp[0][j] = Math.max(dp[0][j - 1], str1[0] == str2[j] ? 1 : 0);
		}
		for (int i = 1; i < str1.length; i++) {
			for (int j = 1; j < str2.length; j++) {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
				if (str1[i] == str2[j]) {
					dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
				}
			}
		}
		return dp[str1.length - 1][str2.length - 1];
	}

	public static int maxLen2(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		int[][] dp = new int[str.length][str.length];
		for (int i = 0; i < str.length; i++) {
			dp[i][i] = 1;
		}
		for (int i = 0; i < str.length - 1; i++) {
			dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
		}
		for (int i = str.length - 2; i >= 0; i--) {
			for (int j = i + 2; j < str.length; j++) {
				dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
				if (str[i] == str[j]) {
					dp[i][j] = Math.max(dp[i + 1][j - 1] + 2, dp[i][j]);
				}
			}
		}
		return dp[0][str.length - 1];
	}

	public static void main(String[] args) {
		String test = "A1BC2D33FG2H1I";
		System.out.println(maxLen1(test));
		System.out.println(maxLen2(test));
	}

}

添加字符让其回文（范围尝试）

给定一个字符串str，如果可以在str的任意位置添加字符，请返回在添加字符最少的情况下，让str整体都是回文字符串的一种结果。

【举例】

str="ABA"。str本身就是回文串，不需要添加字符，所以返回"ABA"。

str="AB"。可以在'A'之前添加'B'，使str整体都是回文串，故可以返回"BAB"。也可以在'B'之后添加'A'，使str整体都是回文串，故也可以返回"ABA"。总之，只要添加的字符数最少，返回其中一种结果即可。

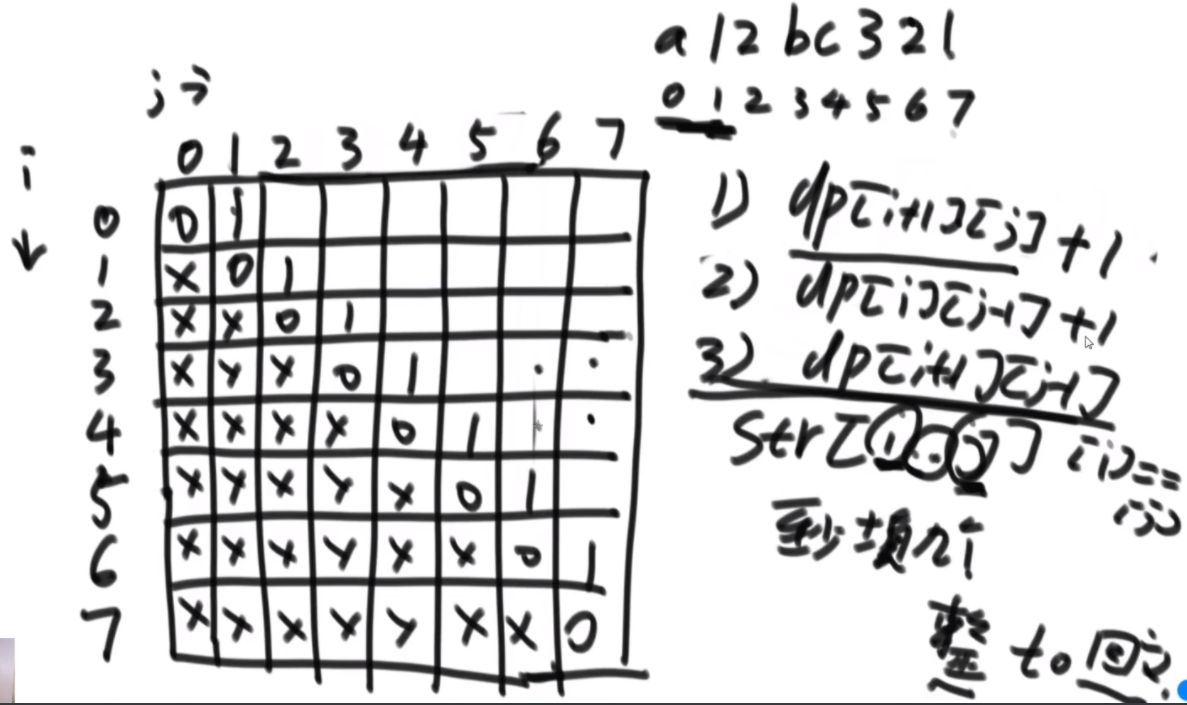
范围上的尝试：dp【i】【j】代表str[i...j]上至少要填几个字符能让整体成为回文结构。左下半区不管，对角线都是0.下一个对角线都是1.开头和结尾字符不一样的话，左边和下边的谁小谁+1就是这个位置的，如果一样，那么就是左下角的。

思路：首先分析可能性，只需要看i和j的各种情况

1. 如果先解决i+1,到j位置的字符，最后再解决i位置的字符，那么dp【i+1】【j】+1
2. 如果先解决i,到j-1位置的字符，最后再解决j位置的字符，那么dp【i】【j-1】+1
3. 如果i位置字符等于j位置字符，就只需要搞定中间位置的字符了，那么dp【i+1】【j-1】

如何还原路径：当时咋整出来的，就继续整回去。

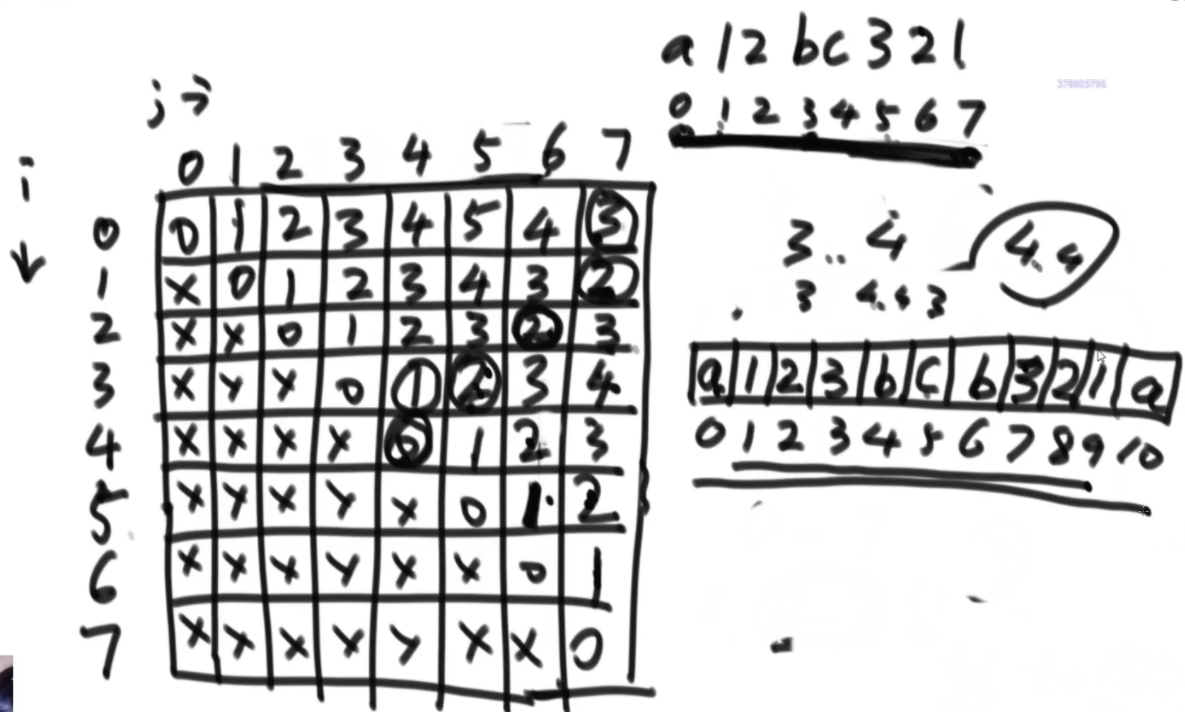
package class04;

public class Problem03_PalindromeMinAdd {

	public static String getPalindrome1(String str) {
		if (str == null || str.length() < 2) {
			return str;
		}
		char[] chas = str.toCharArray();
		int[][] dp = getDP(chas);
		char[] res = new char[chas.length + dp[0][chas.length - 1]];
		int i = 0;
		int j = chas.length - 1;
		int resl = 0;
		int resr = res.length - 1;
		while (i <= j) {
			if (chas[i] == chas[j]) {
				res[resl++] = chas[i++];
				res[resr--] = chas[j--];
			} else if (dp[i][j - 1] < dp[i + 1][j]) {
				res[resl++] = chas[j];
				res[resr--] = chas[j--];
			} else {
				res[resl++] = chas[i];
				res[resr--] = chas[i++];
			}
		}
		return String.valueOf(res);
	}

	public static int[][] getDP(char[] str) {
		int[][] dp = new int[str.length][str.length];
		for (int j = 1; j < str.length; j++) {
			dp[j - 1][j] = str[j - 1] == str[j] ? 0 : 1;
			for (int i = j - 2; i > -1; i--) {
				if (str[i] == str[j]) {
					dp[i][j] = dp[i + 1][j - 1];
				} else {
					dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
				}
			}
		}
		return dp;
	}

	public static void main(String[] args) {
		String str = "AB1CD2EFG3H43IJK2L1MN";
		System.out.println(getPalindrome1(str));
	}

}

str切成回文子串的最小切割数

给定一个字符串str，返回把str全部切成回文子串的最小分割数。

【举例】

str="ABA"。不需要切割，str本身就是回文串，所以返回0。

str="ACDCDCDAD"。最少需要切2次变成3个回文子串，比如"A"、"CDCDC"和"DAD"，所以返回2。

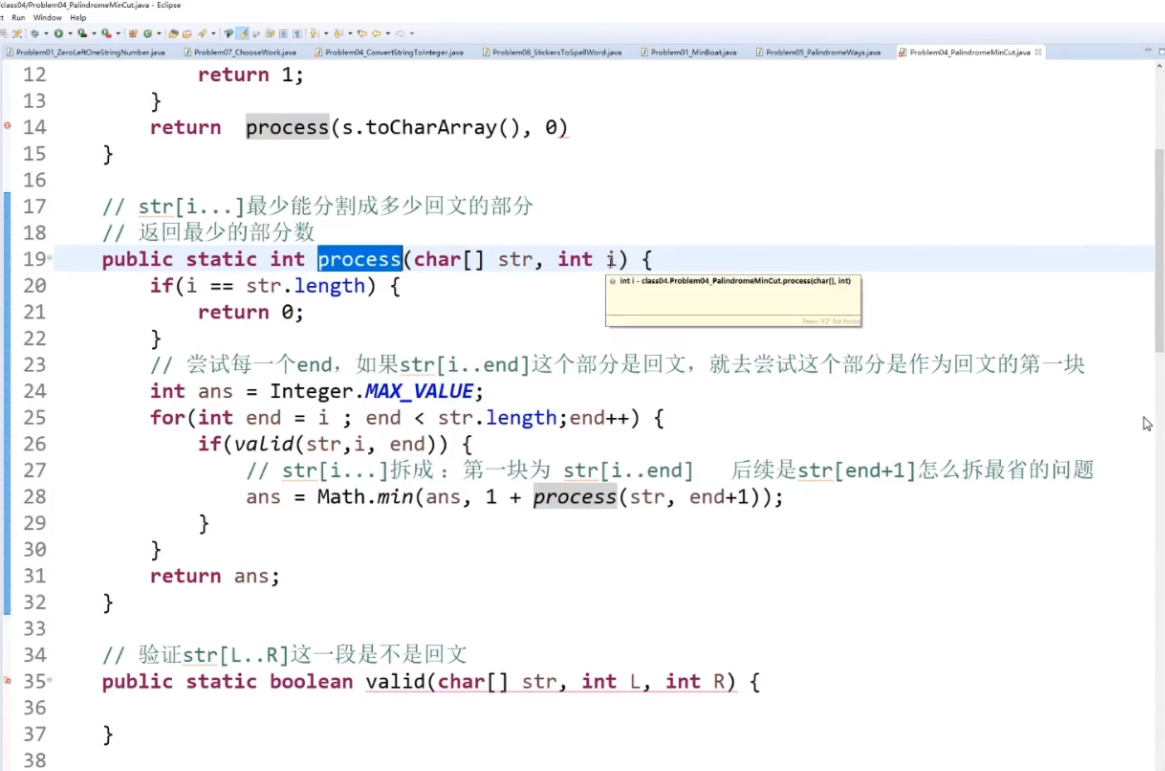
思路：首先整体上这个题是从左往右的模型，然后先看第一块，然后如果是回文然后拆分成两块加上后面的切分次数。这样的结果是O(N³)，因为你判断是否是回文依旧会是一个O(N)的操作，所以优化一下：对是否是回文搞一个数组来让其成为一个O(1)的操作，判断过程可以是范围尝试的模型，然后这个就优化成O(N²)了。

package class04;

public class Problem04_PalindromeMinCut {

	public static int minCut(String str) {
		if (str == null || str.equals("")) {
			return 0;
		}
		char[] chas = str.toCharArray();
		int len = chas.length;
		int[] dp = new int[len + 1];
		dp[len] = -1;
		boolean[][] p = new boolean[len][len];
		for (int i = len - 1; i >= 0; i--) {
			dp[i] = Integer.MAX_VALUE;
			for (int j = i; j < len; j++) {
				if (chas[i] == chas[j] && (j - i < 2 || p[i + 1][j - 1])) {
					p[i][j] = true;
					dp[i] = Math.min(dp[i], dp[j + 1] + 1);
				}
			}
		}
		return dp[0];
	}

	// for test
	public static String getRandomStringOnlyAToD(int len) {
		int range = 'D' - 'A' + 1;
		char[] charArr = new char[(int) (Math.random() * (len + 1))];
		for (int i = 0; i != charArr.length; i++) {
			charArr[i] = (char) ((int) (Math.random() * range) + 'A');
		}
		return String.valueOf(charArr);
	}

	public static void main(String[] args) {
		int maxLen = 10;
		int testTimes = 5;
		String str = null;
		for (int i = 0; i != testTimes; i++) {
			str = getRandomStringOnlyAToD(maxLen);
			System.out.print("\"" + str + "\"" + " : ");
			System.out.println(minCut(str));
		}

	}
}

移除字符使s变为回文

对于一个字符串, 从前开始读和从后开始读是一样的, 我们就称这个字符串是回文串。例如"ABCBA","AA", "A" 是回文串, 而"ABCD", "AAB"不是回文串。牛牛特别喜欢回文串, 他手中有一个字符串s, 牛牛在思考能否从字符串中移除部分(0个或多个)字符使其变为回文串，并且牛牛认为空串不是回文串。牛牛发现移除的方案可能有 很多种, 希望你来帮他计算一下一共有多少种移除方案可以使s变为回文串。对于两种移除方案, 如果移除的字符依次构成的序列不一样就是不同的方案。

例如，XXY 4种 ABA 5种

【说明】 这是今年的原题，提供的说明和例子都很让人费解。现在根据当时题目的所有测试用例，重新解释当时的题目含义：

1）"1AB23CD21"，你可以选择删除A、B、C、D，然后剩下子序列{1,2,3,2,1}，只要剩下的子序列是同一个，那么就只算1种方法，和A、B、C、D选择什么样的删除顺序没有关系。

2）"121A1"，其中有两个{1,2,1}的子序列，第一个{1,2,1}是由{位置0，位置1，位置2}构成，第二个{1,2,1} 是由{位置0，位置1，位置4}构成。这两个子序列被认为是不同的子序列。也就是说在本题中，认为字面值一样但是位置不同的字符就是不同的。

3）其实这道题是想求，str中有多少个不同的子序列，每一种子序列只对应一种删除方法，那就是把多余的东西去掉，而和去掉的顺序无关。

4）也许你觉得我的解释很荒谬，但真的是这样，不然解释不了为什么，XXY 4种 ABA 5种，而且其他的测试用例都印证了这一点。

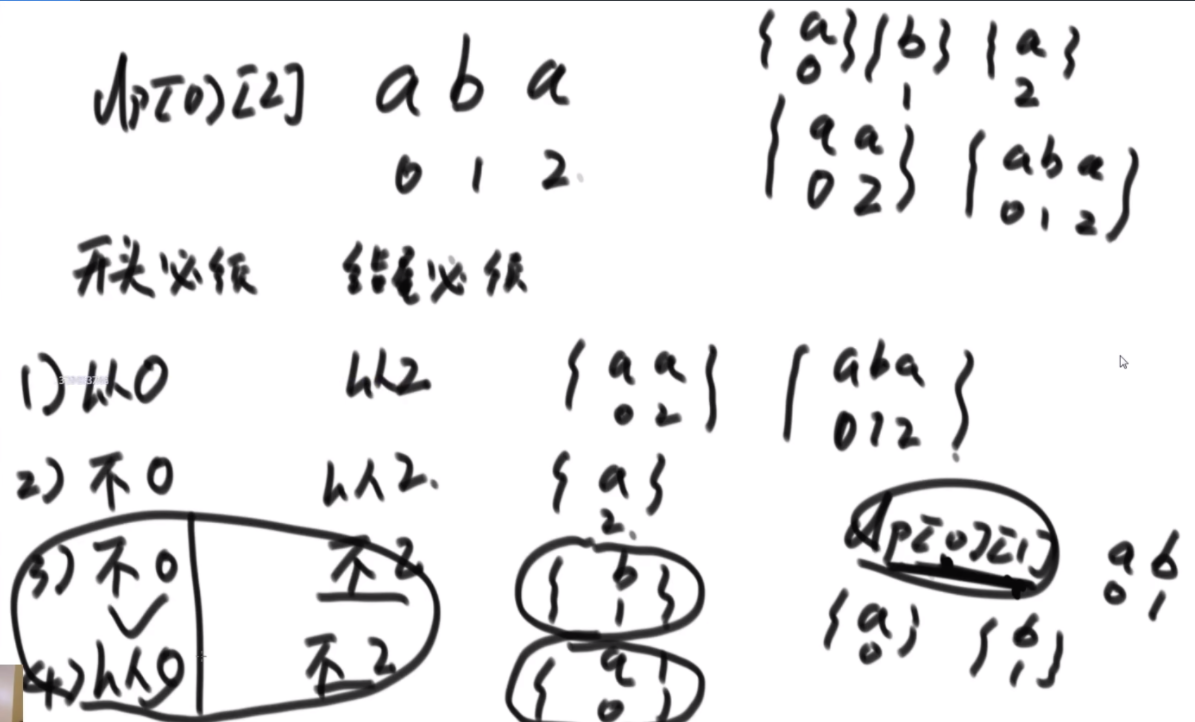
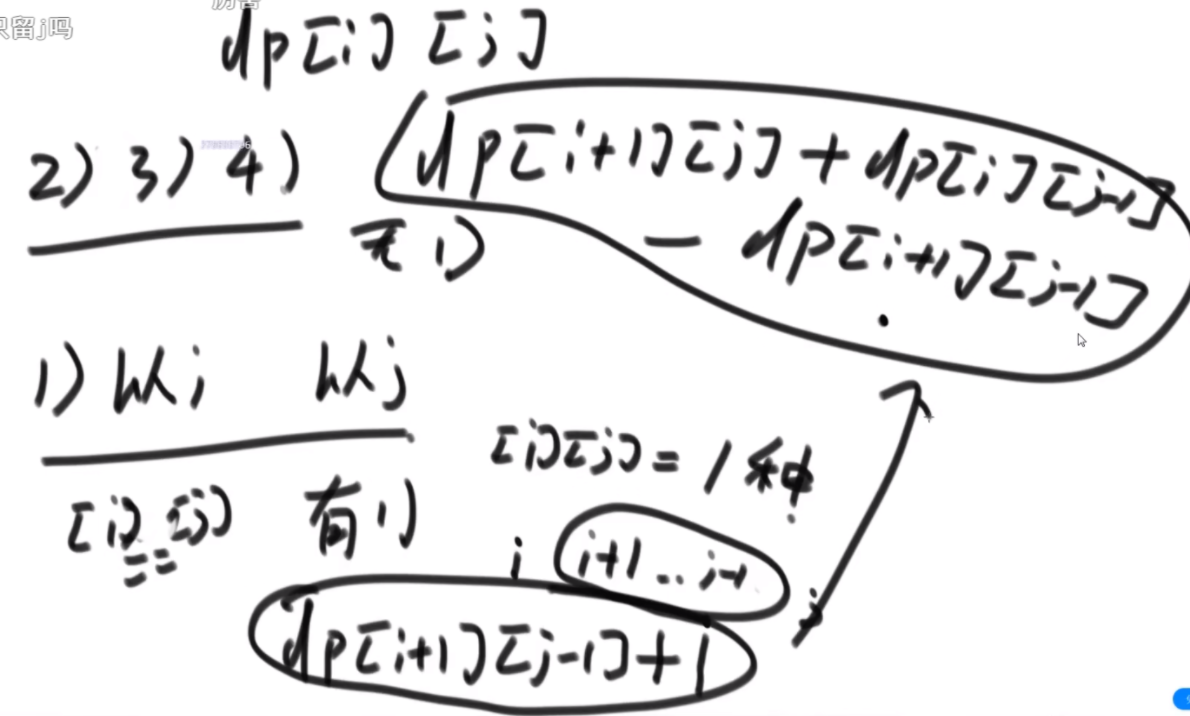
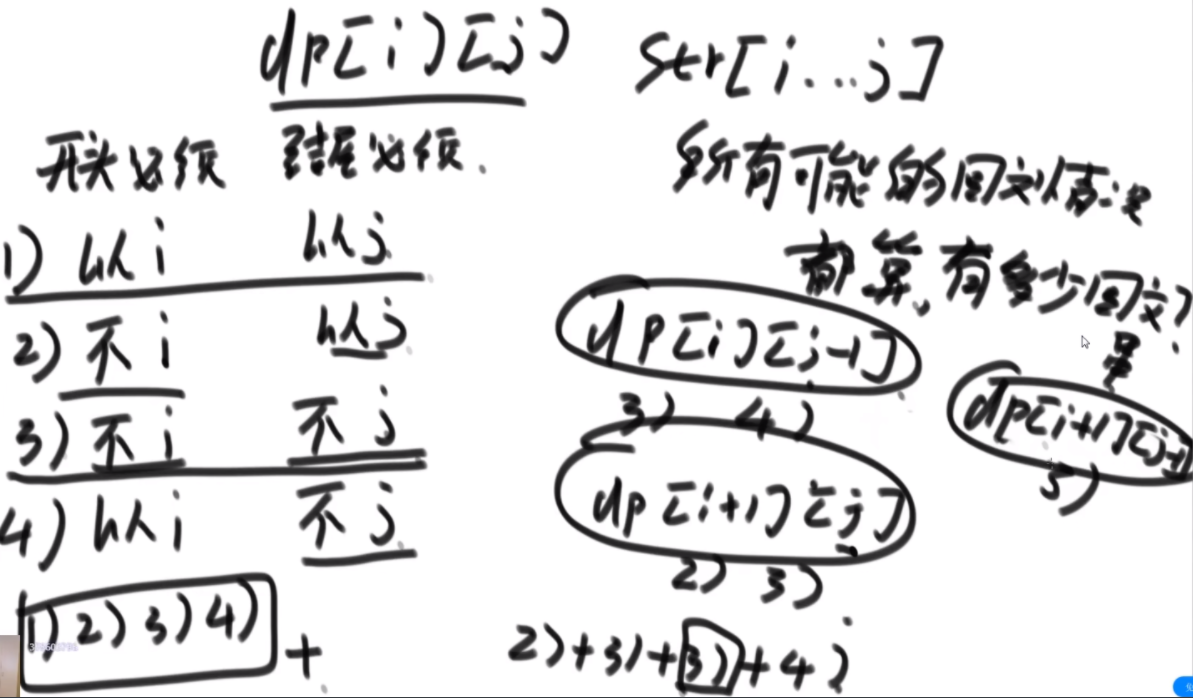
思路：首先是分为4种情况，开头必须是从i开始，或者不是，结尾必须是j或者不是，这俩可以组合出4中。然后dp【i】【j-1】代表了3和4情况，dp【i+1】【j】代表了2和3情况，dp【i+1】【j+1】代表3情况，可以通过左下图中上面的公式加出2 3 4，1情况：如果i和j不相等，那么不用管，如果相等，那么是dp【i+1】【j-1】+1.把四种情况加起来即可。

package class04;

public class Problem05_PalindromeWays {

	public static int way1(String str) {
		char[] s = str.toCharArray();
		int len = s.length;
		int[][] dp = new int[len + 1][len + 1];
		for (int i = 0; i <= len; i++) {
			dp[i][i] = 1;
		}
		for (int subLen = 2; subLen <= len; subLen++) {
			for (int l = 1; l <= len - subLen + 1; l++) {
				int r = l + subLen - 1;
				dp[l][r] += dp[l + 1][r];
				dp[l][r] += dp[l][r - 1];
				if (s[l - 1] == s[r - 1])
					dp[l][r] += 1;
				else
					dp[l][r] -= dp[l + 1][r - 1];
			}
		}
		return dp[1][len];
	}

	public static int way2(String str) {
		char[] s = str.toCharArray();
		int n = s.length;
		int[][] dp = new int[100][100];
		for (int i = 0; i < n; i++) {
			dp[i][i] = 1;
			if (i + 1 < n && s[i] == s[i + 1])
				dp[i][i + 1] = 3;
			else
				dp[i][i + 1] = 2;
		}
		for (int p = 2; p < n; ++p) {
			for (int i = 0, j = p; j < n; ++i, ++j)
				if (s[i] == s[j])
					dp[i][j] = dp[i + 1][j] + dp[i][j - 1] + 1;
				else
					dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1];
		}
		return dp[0][n - 1];
	}

	public static void main(String[] args) {
		System.out.println(way1("ABA"));
		System.out.println(way1("XX"));
		System.out.println(way1("ABA"));

		System.out.println(way2("XXY"));
		System.out.println(way2("XX"));
		System.out.println(way2("ABA"));
	}

}

p33:

26伪进制

一个 char 类型的数组 chs，其中所有的字符都不同。例如，chs=['A', 'B', 'C', ... 'Z']，则字符串与整数的对应关系如下:

A, B... Z, AA,AB...AZ,BA,BB...ZZ,AAA... ZZZ, AAAA...

1, 2...26,27, 28... 52,53,54...702,703...18278, 18279...

例如，chs=['A', 'B', 'C']，则字符串与整数的对应关系如下:

A,B,C,AA,AB...CC,AAA...CCC,AAAA...

1, 2,3,4,5...12,13...39,40...

给定一个数组 chs，实现根据对应关系完成字符串与整数相互转换的两个函数。

思路：这个题是K伪进制，假设是3伪进制表示10，那么应该是从3⁰放一个1，然后还剩9，然后3¹放一个1，还剩6，3²没法放，那么回来继续，3¹再加2就是结果。伪进制就是每个位置必须有一个1，然后走到头走不了了再走回来。这个题是26伪进制。

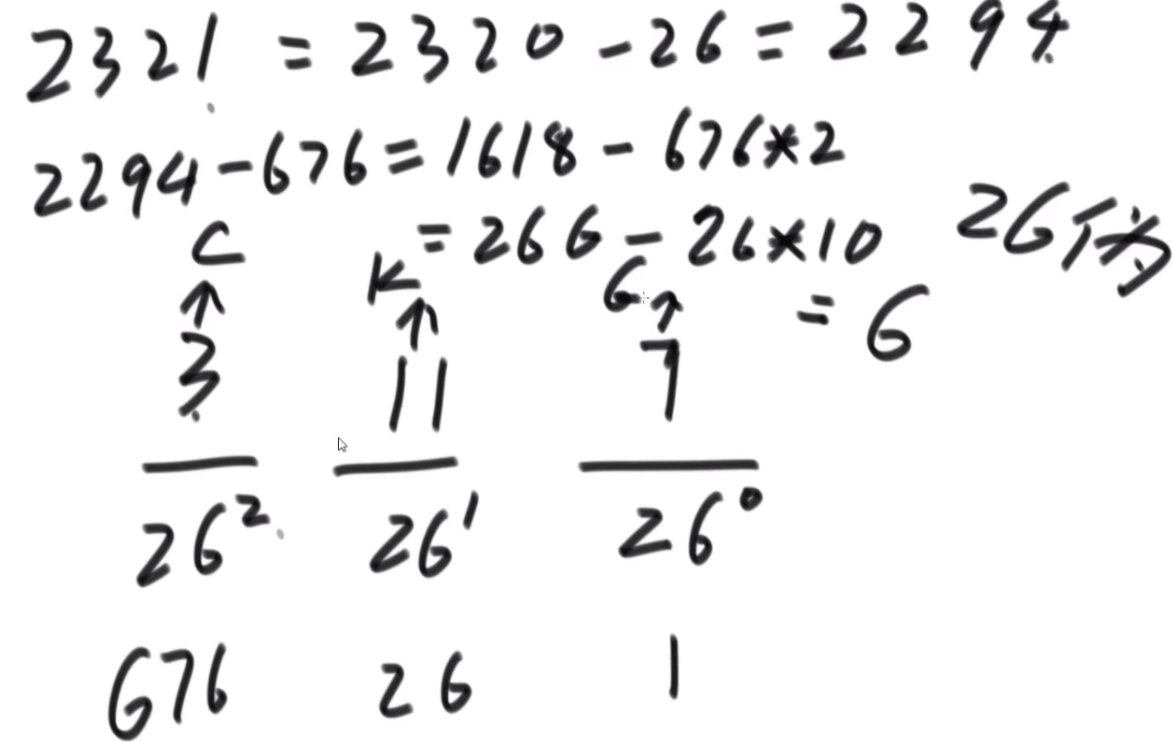
package class02;

public class Problem05_NumberAndString {

	public static String getString(char[] chs, int n) {
		if (chs == null || chs.length == 0 || n < 1) {
			return "";
		}
		int cur = 1;
		int base = chs.length;
		int len = 0;
		while (n >= cur) {
			len++;
			n -= cur;
			cur *= base;
		}
		char[] res = new char[len];
		int index = 0;
		int nCur = 0;
		do {
			cur /= base;
			nCur = n / cur;
			res[index++] = getKthCharAtChs(chs, nCur + 1);
			n %= cur;
		} while (index != res.length);
		return String.valueOf(res);
	}

	public static char getKthCharAtChs(char[] chs, int k) {
		if (k < 1 || k > chs.length) {
			return 0;
		}
		return chs[k - 1];
	}

	public static int getNum(char[] chs, String str) {
		if (chs == null || chs.length == 0) {
			return 0;
		}
		char[] strc = str.toCharArray();
		int base = chs.length;
		int cur = 1;
		int res = 0;
		for (int i = strc.length - 1; i != -1; i--) {
			res += getNthFromChar(chs, strc[i]) * cur;
			cur *= base;
		}
		return res;
	}

	public static int getNthFromChar(char[] chs, char ch) {
		int res = -1;
		for (int i = 0; i != chs.length; i++) {
			if (chs[i] == ch) {
				res = i + 1;
				break;
			}
		}
		return res;
	}

	public static void main(String[] args) {
		char[] chs = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K',
				'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W',
				'X', 'Y', 'Z' };
		int len = 1;
		String res = "";
		for (int i = 1; i != 705; i++) {
			res = getString(chs, i);
			if (res.length() != len) {
				len = res.length();
				System.out.println("================");
			}
			System.out.print(res + " ");
			if (i % chs.length == 0) {
				System.out.println();
			}
		}
		System.out.println();
		System.out.println("========================");
		int testNum = 78128712;
		System.out.println(getNum(chs, getString(chs, testNum)));
		String testStr = "BZZA";
		System.out.println(getString(chs, getNum(chs, testStr)));

	}
}

贪吃蛇最长能吃到多长

给定一个二维数组matrix，每个单元都是一个整数，有正有负。最开始的时候小Q操纵一条长度为0的蛇蛇从矩阵最左侧任选一个单元格进入地图，蛇每次只能够到达当前位置的右上相邻，右侧相邻和右下相邻的单元格。蛇蛇到达一个单元格后，自身的长度会瞬间加上该单元格的数值，任何情况下长度为负则游戏结束。小Q是个天才，他拥有一个超能力，可以在游戏开始的时候把地图中的某一个节点的值变为其相反数（注：最多只能改变一个节点）。问在小Q游戏过程中，他的蛇蛇最长长度可以到多少？

比如：

1 -4 10

3 -2 -1

2 -1 0

0 5 -2

最优路径为从最左侧的3开始，3 -> -4(利用能力变成4) -> 10。所以返回17。

思路：分析这个蛇从最左侧开始走，每次往下递归的时候分成用了技能和没用技能，每次移动的时候会从左上左侧和左下三个位置过来，取最大的值。

优化：记忆化搜索（即缓存），搞一个dp数组记录这些，动态规划：利用数组中元素的相互关系直接计算出结果，无需递归。

package class03;

public class Problem02_SnakeGame {

	public static int walk1(int[][] matrix) {
		if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
			return 0;
		}
		int res = Integer.MIN_VALUE;
		for (int i = 0; i < matrix.length; i++) {
			int[] ans = process(matrix, i, 0);
			res = Math.max(res, Math.max(ans[0], ans[1]));
		}
		return res;
	}

	// 从(i,j)出发一直走到最右侧的旅程中
	// 0) 在没有使用过能力的情况下，返回路径最大和
	// 1) 在使用过能力的情况下，返回路径最大和
	public static int[] process(int[][] m, int i, int j) {
		if (j == m[0].length - 1) {
			return new int[] { m[i][j], -m[i][j] };
		}
		int[] restAns = process(m, i, j + 1);
		int restUnuse = restAns[0];
		int restUse = restAns[1];
		if (i - 1 >= 0) {
			restAns = process(m, i - 1, j + 1);
			restUnuse = Math.max(restUnuse, restAns[0]);
			restUse = Math.max(restUse, restAns[1]);
		}
		if (i + 1 < m.length) {
			restAns = process(m, i + 1, j + 1);
			restUnuse = Math.max(restUnuse, restAns[0]);
			restUse = Math.max(restUse, restAns[1]);
		}
		int no = m[i][j] + restUnuse;
		int yes = Math.max(m[i][j] + restUse, -m[i][j] + restUnuse);
		return new int[] { no, yes };
	}

	public static int walk2(int[][] matrix) {
		if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
			return 0;
		}
		int[][][] dp = new int[matrix.length][matrix[0].length][2];
		for (int i = 0; i < dp.length; i++) {
			dp[i][matrix[0].length - 1][0] = matrix[i][matrix[0].length - 1];
			dp[i][matrix[0].length - 1][1] = -matrix[i][matrix[0].length - 1];
		}
		for (int j = matrix[0].length - 2; j >= 0; j--) {
			for (int i = 0; i < matrix.length; i++) {
				int restUnuse = dp[i][j + 1][0];
				int restUse = dp[i][j + 1][1];
				if (i - 1 >= 0) {
					restUnuse = Math.max(restUnuse, dp[i - 1][j + 1][0]);
					restUse = Math.max(restUse, dp[i - 1][j + 1][1]);
				}
				if (i + 1 < matrix.length) {
					restUnuse = Math.max(restUnuse, dp[i + 1][j + 1][0]);
					restUse = Math.max(restUse, dp[i + 1][j + 1][0]);
				}
				dp[i][j][0] = matrix[i][j] + restUnuse;
				dp[i][j][1] = Math.max(matrix[i][j] + restUse, -matrix[i][j] + restUnuse);
			}
		}

		int res = Integer.MIN_VALUE;
		for (int i = 0; i < matrix.length; i++) {
			res = Math.max(res, Math.max(dp[i][0][0], dp[i][0][1]));
		}
		return res;
	}

	public static void main(String[] args) {
		int[][] matrix = { { 1, -4, 10 }, { 3, -2, -1 }, { 2, -1, 0 }, { 0, 5, -2 } };
		System.out.println(walk1(matrix));
		System.out.println(walk2(matrix));
	}

}

公式字符串计算答案

给定一个字符串str，str表示一个公式，公式里可能有整数、加减乘除符号和左右括号，返回公式的计算结果。

【举例】 str="48((70-65)-43)+81"，返回-1816。 str="3+14"，返回7。 str="3+(14)"，返回7。

【说明】 1．可以认为给定的字符串一定是正确的公式，即不需要对str做公式有效性检查。2．如果是负数，就需要用括号括起来，比如"4(-3)"。但如果负数作为公式的开头或括号部分的开头，则可以没有括号，比如"-34"和"(-3*4)"都是合法的。3．不用考虑计算过程中会发生溢出的情况。

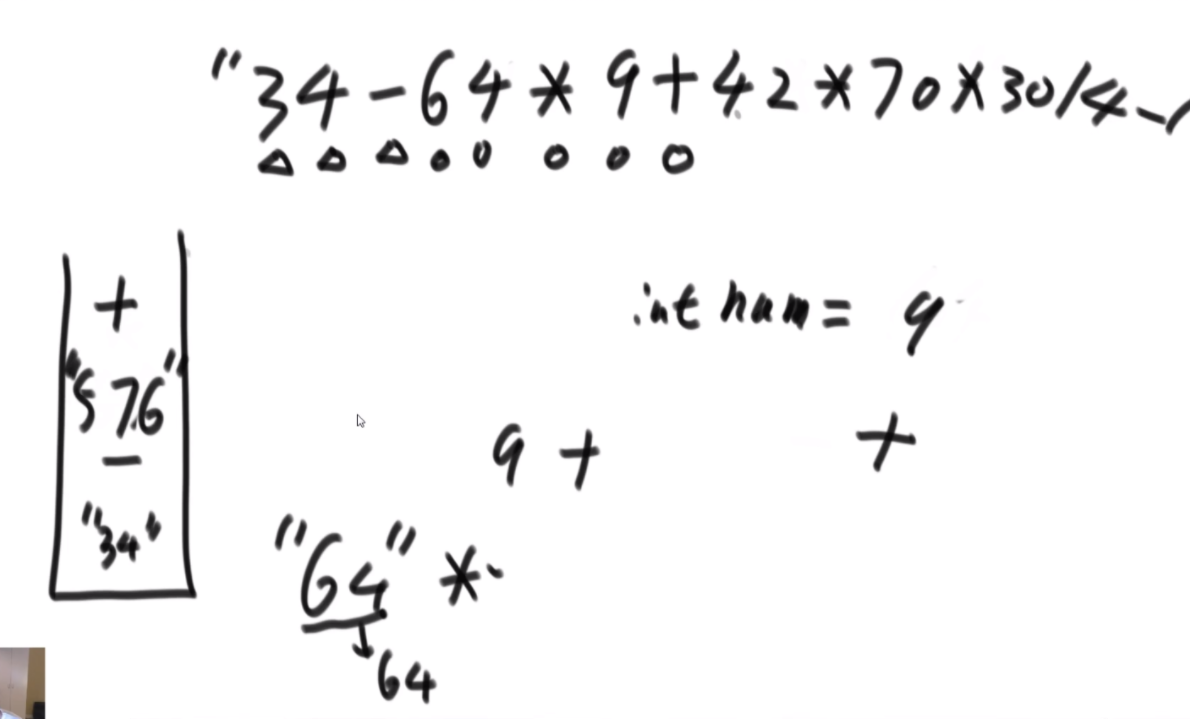
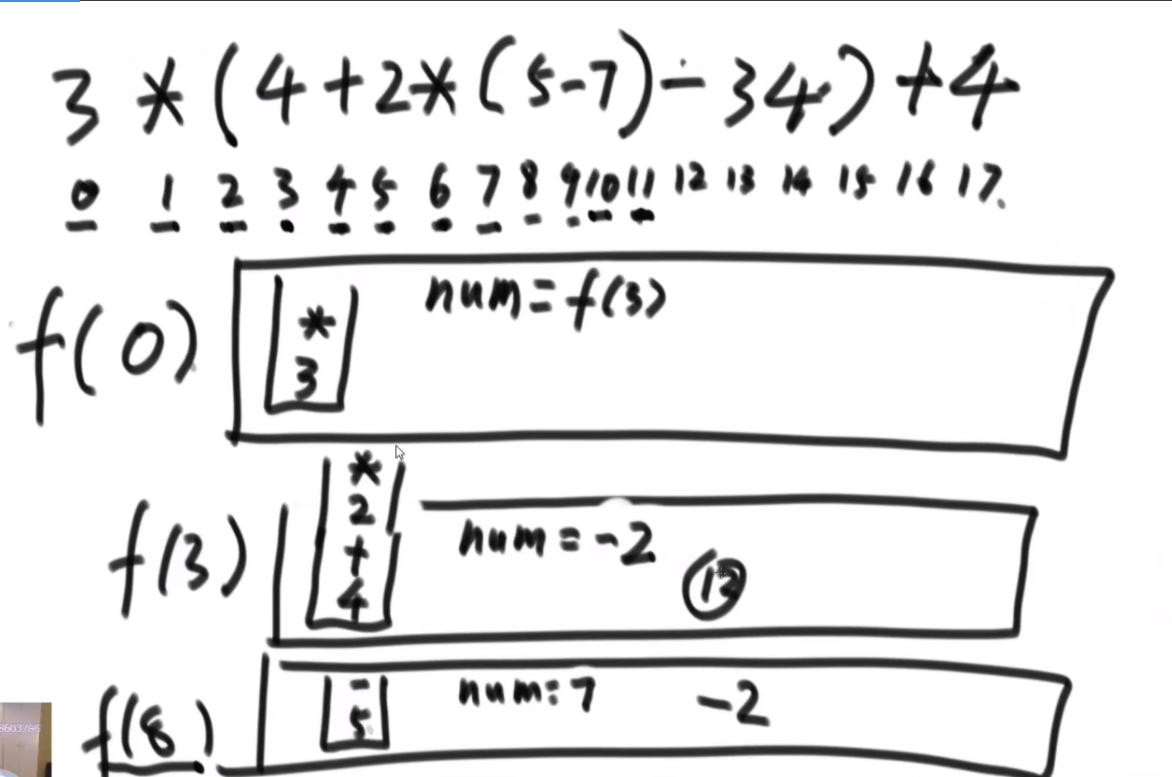
思路：这种字符串可以分为有括号和没括号的两种情况。首先看没括号的时候，搞一个栈，一个num，3读入，num=3，4读入，num=34，-读入，进入栈，后面一直到9进入的时候，遇到+号，符号每次入栈之前要看里面栈顶符号是不是乘号或者除号，如果是的话那必须先拿出来计算完放进去后再继续走。这样走到最后栈里面就只有数字和加减号。第二种情况是有括号的时候，每次遇到左括号就会进入下一层递归，然后这个递归从左括号的下一个开始记录，每次都去进，直到遇见右括号，结算当前递归然后返回结果和当前位置，方便上个递归好找位置。

package class03;

import java.util.LinkedList;

public class Problem03_ExpressionCompute {

	public static int getValue(String str) {
		return value(str.toCharArray(), 0)[0];
	}

	//请从str[i...]往下算，遇到字符串终止位置或者右括号，就停止
	//返回两个值，长度为2的数组
	//0)负责的这一段的结果是多少
	//1)负责的这一段计算到了哪个位置
	public static int[] value(char[] str, int i) {
		LinkedList<String> que = new LinkedList<String>();
		int pre = 0;
		int[] bra = null;
		while (i < str.length && str[i] != ')') {
			if (str[i] >= '0' && str[i] <= '9') {
				pre = pre * 10 + str[i++] - '0';
			} else if (str[i] != '(') {//遇到的是运算符号
				addNum(que, pre);
				que.addLast(String.valueOf(str[i++]));
				pre = 0;
			} else {//遇到左括号了
				bra = value(str, i + 1);
				pre = bra[0];
				i = bra[1] + 1;
			}
		}
		addNum(que, pre);
		return new int[] { getNum(que), i };
	}

	public static void addNum(LinkedList<String> que, int num) {
		if (!que.isEmpty()) {
			int cur = 0;
			String top = que.pollLast();
			if (top.equals("+") || top.equals("-")) {
				que.addLast(top);
			} else {
				cur = Integer.valueOf(que.pollLast());
				num = top.equals("*") ? (cur * num) : (cur / num);
			}
		}
		que.addLast(String.valueOf(num));
	}

	public static int getNum(LinkedList<String> que) {
		int res = 0;
		boolean add = true;
		String cur = null;
		int num = 0;
		while (!que.isEmpty()) {
			cur = que.pollFirst();
			if (cur.equals("+")) {
				add = true;
			} else if (cur.equals("-")) {
				add = false;
			} else {
				num = Integer.valueOf(cur);
				res += add ? num : (-num);
			}
		}
		return res;
	}

	public static void main(String[] args) {
		String exp = "48*((70-65)-43)+8*1";
		System.out.println(getValue(exp));

		exp = "4*(6+78)+53-9/2+45*8";
		System.out.println(getValue(exp));

		exp = "10-5*3";
		System.out.println(getValue(exp));

		exp = "-3*4";
		System.out.println(getValue(exp));

		exp = "3+1*4";
		System.out.println(getValue(exp));

	}

}

两个字符串的最长公共子串

请注意区分子串和子序列的不同，给定两个字符串str1和str2，求两个字符串的最长公共子串。 子串要求连续，子序列只要求相对位置

动态规划空间压缩的技巧讲解

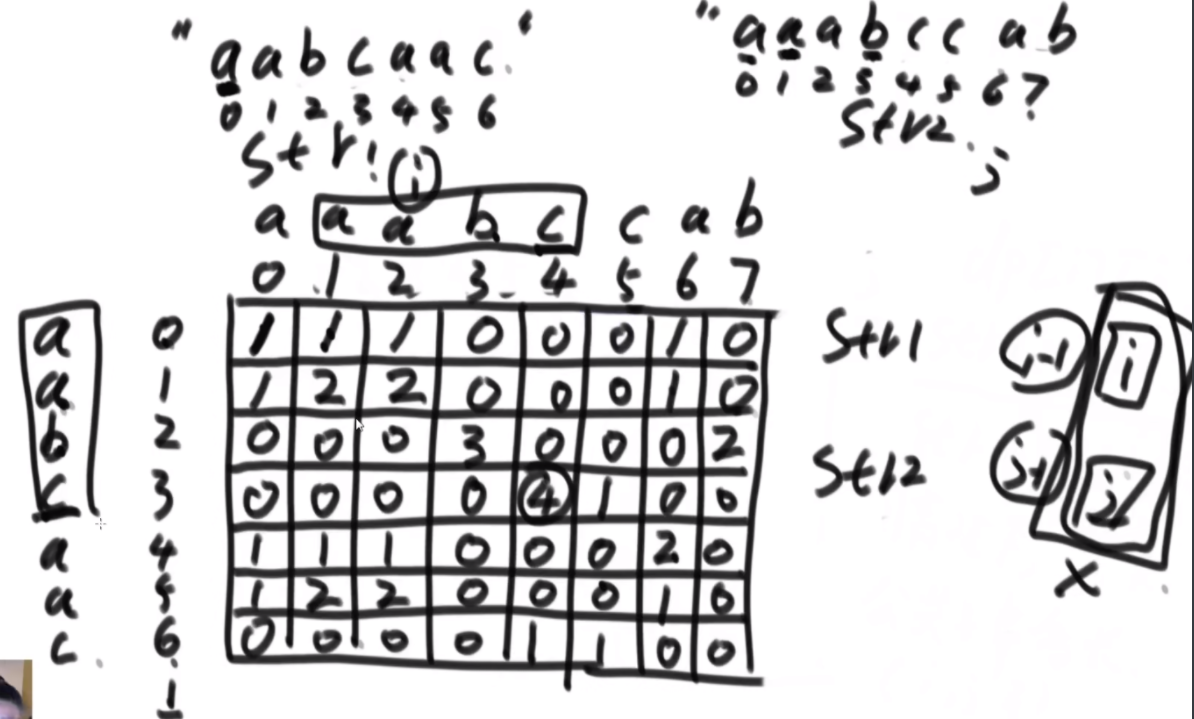
思路：首先是没有压缩空间的时候的解，搞一个二维表，行代表的是str1，列是str2，坐标代表的是，假设公共子串以i和j位置结尾，然后如果这俩位置的str对应的字符不相等那么长度一定为0，然后第一行和第一列（这里是因为长度为1，如果相同就长度为1不同就为0）以及所有字符结尾不同的都为0.然后如果相同，那么就是左上角位置的值+1就是这个位置的值，代表如果这俩字符串上个位置也相同那么这个位置就可以续上，如果当前位置不同，那么该位置为0.

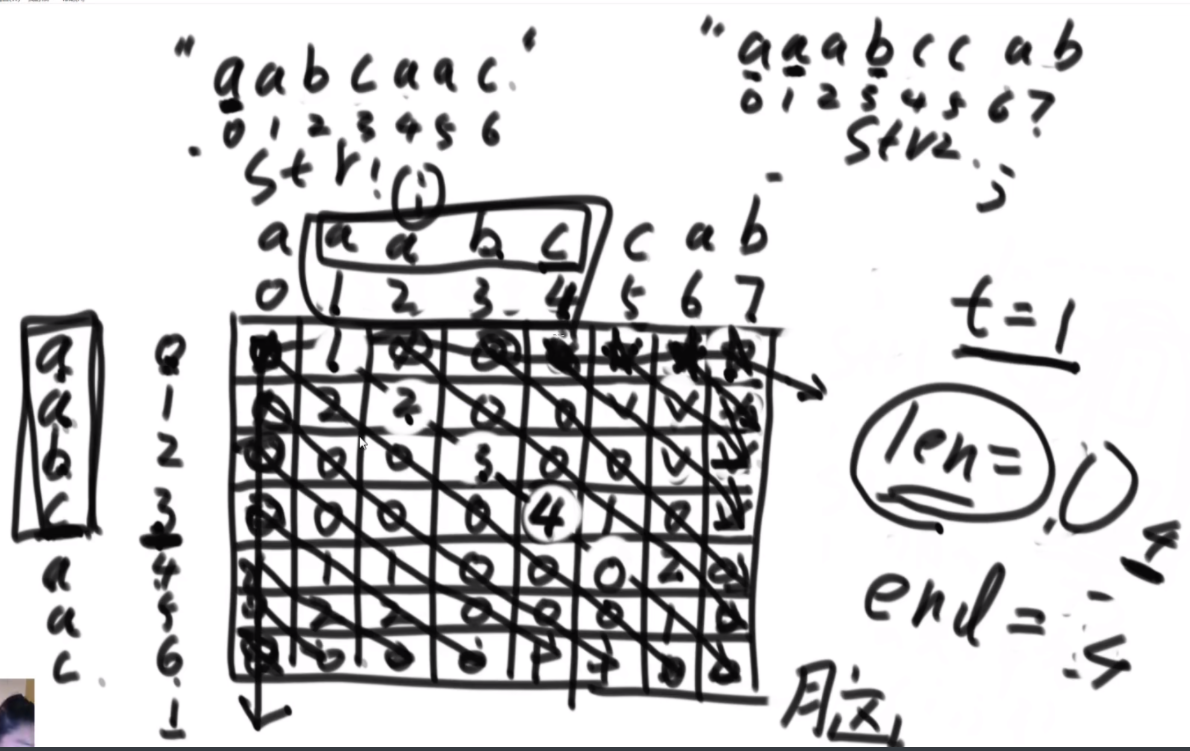
优化：用几个变量来完成这个过程，t记录左上角的位置，然后遍历顺序是先最后一列向左，然后向下，就是斜线的顺序，具体看注释。

package class03;

public class Problem04_LCSubstring {

	public static String lcst1(String str1, String str2) {
		if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
			return "";
		}
		char[] chs1 = str1.toCharArray();
		char[] chs2 = str2.toCharArray();
		int[][] dp = getdp(chs1, chs2);
		int end = 0;
		int max = 0;
		for (int i = 0; i < chs1.length; i++) {
			for (int j = 0; j < chs2.length; j++) {
				if (dp[i][j] > max) {
					end = i;
					max = dp[i][j];
				}
			}
		}
		return str1.substring(end - max + 1, end + 1);
	}

	public static int[][] getdp(char[] str1, char[] str2) {
		int[][] dp = new int[str1.length][str2.length];
		for (int i = 0; i < str1.length; i++) {
			if (str1[i] == str2[0]) {
				dp[i][0] = 1;
			}
		}
		for (int j = 1; j < str2.length; j++) {
			if (str1[0] == str2[j]) {
				dp[0][j] = 1;
			}
		}
		for (int i = 1; i < str1.length; i++) {
			for (int j = 1; j < str2.length; j++) {
				if (str1[i] == str2[j]) {
					dp[i][j] = dp[i - 1][j - 1] + 1;
				}
			}
		}
		return dp;
	}

	public static String lcst2(String str1, String str2) {
		if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
			return "";
		}
		char[] chs1 = str1.toCharArray();
		char[] chs2 = str2.toCharArray();
		int row = 0; // 斜线开始位置的行
		int col = chs2.length - 1; // 斜线开始位置的列
		int max = 0; // t达到的全局最大值	
		int end = 0; // 记录的是最大值的时候，子串1的脚标，这样方便往回推
		while (row < chs1.length) {
			int i = row;		
			int j = col;
			int len = 0;//左上角的值
			while (i < chs1.length && j < chs2.length) {
				if (chs1[i] != chs2[j]) {//如果这俩值不相等，无事发生
					len = 0;
				} else {//如果这俩值相等，那么左上角的值+1然后向右下角移动
					len++;
				}
					end = i;
					max = len;
				}
				i++;
				j++;
			}
			if (col > 0) { 
				col--;
			} else { 
				row++;
			}
		}
		return str1.substring(end - max + 1, end + 1);
	}

	public static void main(String[] args) {
		String str1 = "ABC1234567DEFG";
		String str2 = "HIJKL1234567MNOP";
		System.out.println(lcst1(str1, str2));
		System.out.println(lcst2(str1, str2));

	}

}

两个字符串的最长公共子序列

请注意区分子串和子序列的不同，给定两个字符串str1和str2，求两个字符串的最长公共子序列 ,子串要求连续，子序列只要求相对位置

动态规划空间压缩的技巧讲解

思路：首先分析可能性，这个子序列的结尾。

1. 如果不以i结尾，也不以j结尾，那么谁也不相关，那么dp【i-1】【j-1】
2. 如果以i结尾，不以j结尾，那么dp【i】【j-1】
3. 如果不以i结尾，以j结尾，那么dp【i-1】【j】
4. 如果以i结尾，也以j结尾，那么dp【i】【j】

package class03;

public class Problem05_LCSubsequence {

	public static String lcse(String str1, String str2) {
		if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
			return "";
		}
		char[] chs1 = str1.toCharArray();
		char[] chs2 = str2.toCharArray();
		int[][] dp = getdp(chs1, chs2);
		int m = chs1.length - 1;
		int n = chs2.length - 1;
		char[] res = new char[dp[m][n]];
		int index = res.length - 1;
		while (index >= 0) {
			if (n > 0 && dp[m][n] == dp[m][n - 1]) {
				n--;
			} else if (m > 0 && dp[m][n] == dp[m - 1][n]) {
				m--;
			} else {
				res[index--] = chs1[m];
				m--;
				n--;
			}
		}
		return String.valueOf(res);
	}

	public static int[][] getdp(char[] str1, char[] str2) {
		int[][] dp = new int[str1.length][str2.length];
		dp[0][0] = str1[0] == str2[0] ? 1 : 0;
		for (int i = 1; i < str1.length; i++) {
			dp[i][0] = Math.max(dp[i - 1][0], str1[i] == str2[0] ? 1 : 0);
		}
		for (int j = 1; j < str2.length; j++) {
			dp[0][j] = Math.max(dp[0][j - 1], str1[0] == str2[j] ? 1 : 0);
		}
		for (int i = 1; i < str1.length; i++) {
			for (int j = 1; j < str2.length; j++) {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
				if (str1[i] == str2[j]) {
					dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
				}
			}
		}
		return dp;
	}

	public static void main(String[] args) {
		String str1 = "A1BC2D3EFGH45I6JK7LMN";
		String str2 = "12OPQ3RST4U5V6W7XYZ";
		System.out.println(lcse(str1, str2));

	}
}

p32:

大楼的轮廓线数组

给定一个 N×3 的矩阵 matrix，对于每一个长度为 3 的小数组 arr，都表示一个大楼的三个数据。arr[0]表示大楼的左边界，arr[1]表示大楼的右边界，arr[2]表示大楼的高度(一定大于 0)。每座大楼的地基都在 X 轴上，大楼之间可能会有重叠，请返回整体的轮廓线数组。

【举例】

matrix = {{2,5,6},{1,7,4},{4,6,7},{3,6,5},{10,13,2},{9,11,3},{12,14,4},{10,12,5}}

返回：{{1,2,4},{2,4,6},{4,6,7},{6,7,4},{9,10,3},{10,12,5},{12,14,4}}

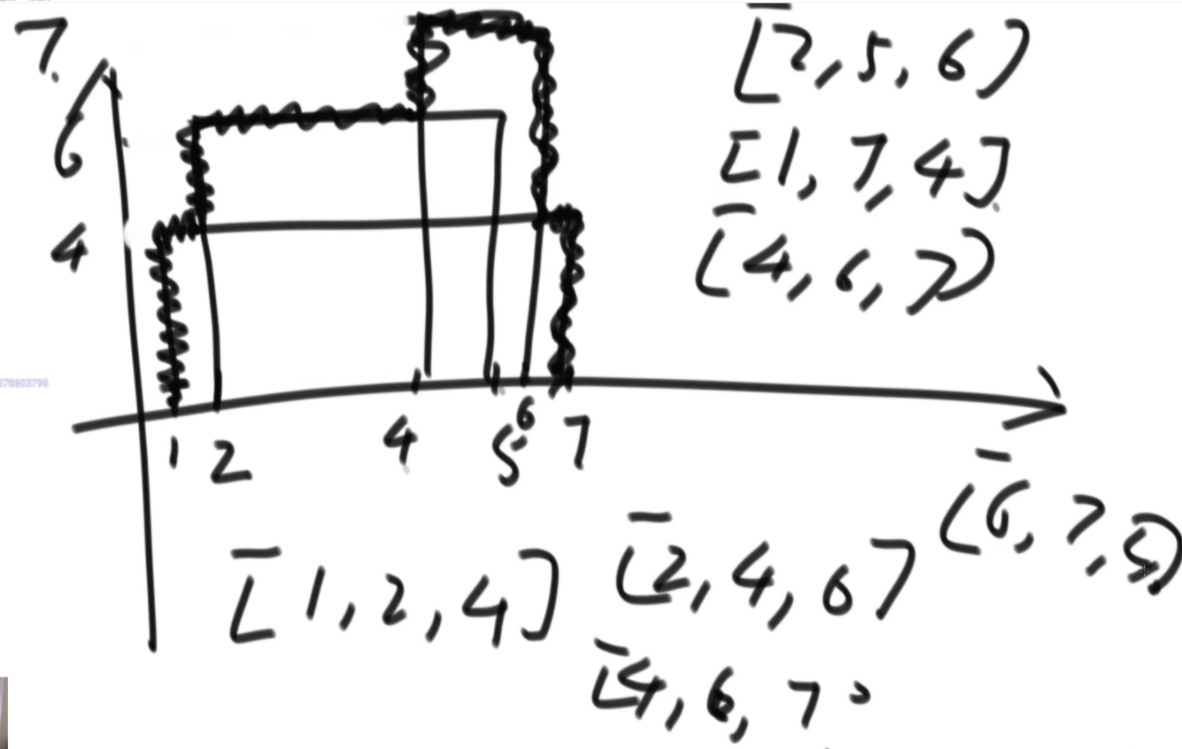
题目：这个数组第一项数据代表这个大楼x轴的起始横坐标，第二项数据代表这个大楼x轴的终止横坐标，第三项数据代表这个大楼的高度。

思路：先遍历这个大楼数组，生成一个长度为大楼数组长度二倍的数组，内容是第一项为x坐标，第二项为增加或者降低高度为一个boolean值，第三项为增加或者降低的高度，这个的排序是第一项小的在前面，第一项相同的增加的在前面。搞一个treemap（有序表，红黑树）去记录高度出现的次数，因为是有序表，所以可以直接拿到最高的高度，因此是按照高度排序的。再搞一个map记录坐标横向遍历的时候，每个位置最大高度是什么（从TreeMap里直接拿最后一个就行）。

package class02;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.Map.Entry;
import java.util.TreeMap;

public class Problem01_BuildingOutline {

	// 描述高度变化的对象
	public static class Node {
		public int x; // x轴上的值
		public boolean isAdd;// true为加入，false为删除
		public int h; // 高度

		public Node(int x, boolean isAdd, int h) {
			this.x = x;
			this.isAdd = isAdd;
			this.h = h;
		}
	}

	// 排序的比较策略
	// 1，第一个维度的x值从小到大。
	// 2，如果第一个维度的值相等，看第二个维度的值，“加入”排在前，“删除”排在后
	// 3，如果两个对象第一维度和第二个维度的值都相等，则认为两个对象相等，谁在前都行。
	public static class NodeComparator implements Comparator<Node> {
		@Override
		public int compare(Node o1, Node o2) {
			if (o1.x != o2.x) {
				return o1.x - o2.x;
			}
			if (o1.isAdd != o2.isAdd) {
				return o1.isAdd ? -1 : 1;
			}
			return 0;
		}
	}

	// 全部流程的主方法
	public static List<List<Integer>> buildingOutline(int[][] matrix) {
		Node[] nodes = new Node[matrix.length * 2];
		// 每一个大楼轮廓数组，产生两个描述高度变化的对象
		for (int i = 0; i < matrix.length; i++) {
			nodes[i * 2] = new Node(matrix[i][0], true, matrix[i][2]);
			nodes[i * 2 + 1] = new Node(matrix[i][1], false, matrix[i][2]);
		}

		// 把描述高度变化的对象数组，按照规定的排序策略排序
		Arrays.sort(nodes, new NodeComparator());

		// TreeMap就是java中的红黑树结构，直接当作有序表来使用
		TreeMap<Integer, Integer> mapHeightTimes = new TreeMap<>();
		TreeMap<Integer, Integer> mapXvalueHeight = new TreeMap<>();
		for (int i = 0; i < nodes.length; i++) {
			if (nodes[i].isAdd) { // 如果当前是加入操作
				if (!mapHeightTimes.containsKey(nodes[i].h)) { // 没有出现的高度直接新加记录
					mapHeightTimes.put(nodes[i].h, 1);
				} else { // 之前出现的高度，次数加1即可
					mapHeightTimes.put(nodes[i].h,
							mapHeightTimes.get(nodes[i].h) + 1);
				}
			} else { // 如果当前是删除操作
				if (mapHeightTimes.get(nodes[i].h) == 1) { // 如果当前的高度出现次数为1，直接删除记录
					mapHeightTimes.remove(nodes[i].h);
				} else { // 如果当前的高度出现次数大于1，次数减1即可
					mapHeightTimes.put(nodes[i].h,
							mapHeightTimes.get(nodes[i].h) - 1);
				}
			}

			// 根据mapHeightTimes中的最大高度，设置mapXvalueHeight表
			if (mapHeightTimes.isEmpty()) { // 如果mapHeightTimes为空，说明最大高度为0
				mapXvalueHeight.put(nodes[i].x, 0);
			} else { // 如果mapHeightTimes不为空，通过mapHeightTimes.lastKey()取得最大高度
				mapXvalueHeight.put(nodes[i].x, mapHeightTimes.lastKey());
			}
		}
		// res为结果数组，每一个List<Integer>代表一个轮廓线，有开始位置，结束位置，高度，一共三个信息
		List<List<Integer>> res = new ArrayList<>();
		// 一个新轮廓线的开始位置
		int start = 0;
		// 之前的最大高度
		int preHeight = 0;
		// 根据mapXvalueHeight生成res数组
		for (Entry<Integer, Integer> entry : mapXvalueHeight.entrySet()) {
			// 当前位置
			int curX = entry.getKey();
			// 当前最大高度
			int curMaxHeight = entry.getValue();
			if (preHeight != curMaxHeight) { // 之前最大高度和当前最大高度不一样时
				if (preHeight != 0) {
					res.add(new ArrayList<>(Arrays.asList(start, curX, preHeight)));
				}
				start = curX;
				preHeight = curMaxHeight;
			}
		}
		return res;
	}

}

正数数组，元素相加为 k 的最长子数组长度

给定一个数组 arr，该数组无序，但每个值均为正数，再给定一个正数 k。求 arr 的所有子数组中所有元素相加和为 k 的最长子数组长度。

例如，arr=[1,2,1,1,1]，k=3。累加和为 3 的最长子数组为[1,1,1]，所以结果返回 3。 要求：时间复杂度O(N)，额外空间复杂度O(1)

思路：搞一个左右指针，用窗口的思想，因为是正数，所以有单调性，LR一开始在初始，然后R一直往右移动，如果相加和超过K那么L移动，这期间最大的长度就是结果。

package class02;

public class Problem02_LongestSumSubArrayLengthInPositiveArray {

	public static int getMaxLength(int[] arr, int k) {
		if (arr == null || arr.length == 0 || k <= 0) {
			return 0;
		}
		int left = 0;
		int right = 0;
		int sum = arr[0];
		int len = 0;
		while (right < arr.length) {
			if (sum == k) {
				len = Math.max(len, right - left + 1);
				sum -= arr[left++];
			} else if (sum < k) {
				right++;
				if (right == arr.length) {
					break;
				}
				sum += arr[right];
			} else {
				sum -= arr[left++];
			}
		}
		return len;
	}

	public static int[] generatePositiveArray(int size) {
		int[] result = new int[size];
		for (int i = 0; i != size; i++) {
			result[i] = (int) (Math.random() * 10) + 1;
		}
		return result;
	}

	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int len = 20;
		int k = 15;
		int[] arr = generatePositiveArray(len);
		printArray(arr);
		System.out.println(getMaxLength(arr, k));

	}

}

无序数组 累加和<= k 的最长子数组长度

给定一个无序数组 arr，其中元素可正、可负、可 0，给定一个整数 k。求 arr 所有的子数组中累加和小于或等于 k 的最长子数组长度。

例如:arr=[3,-2,-4,0,6]，k=-2，相加和小于或等于-2 的最长子数组为{3,-2,-4,0}，所以结果返回4。

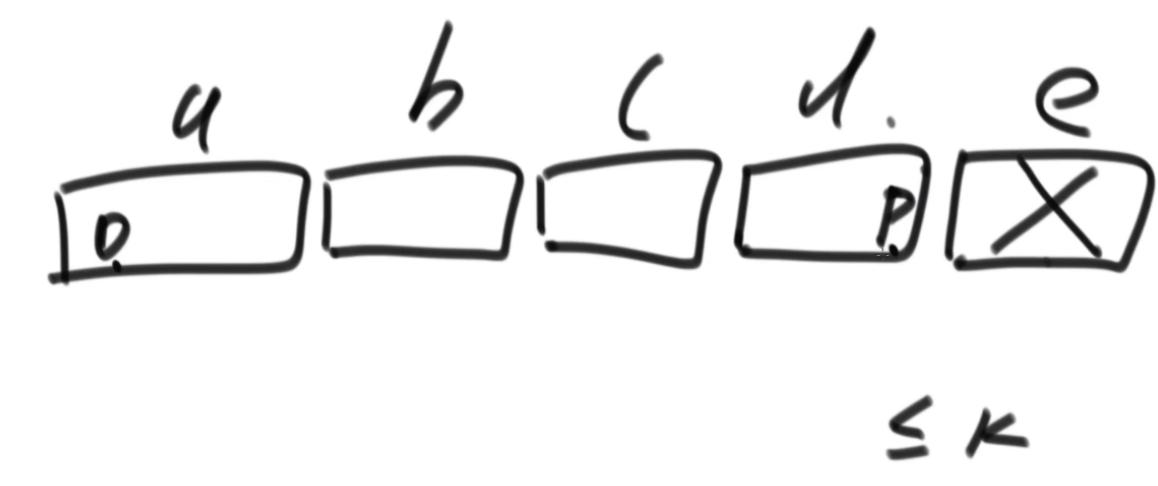
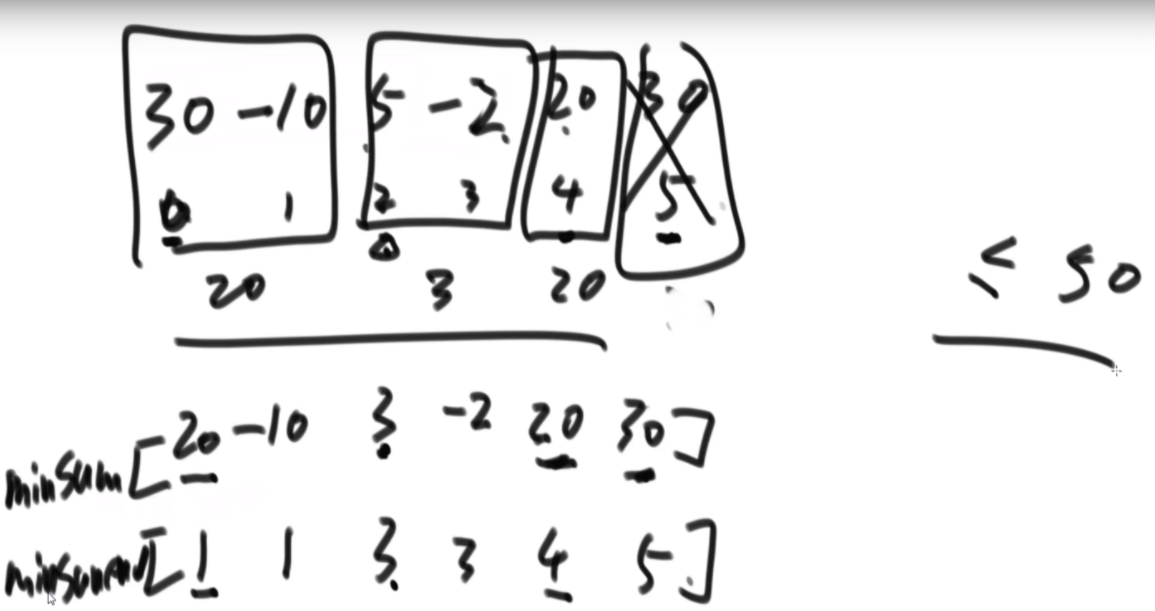
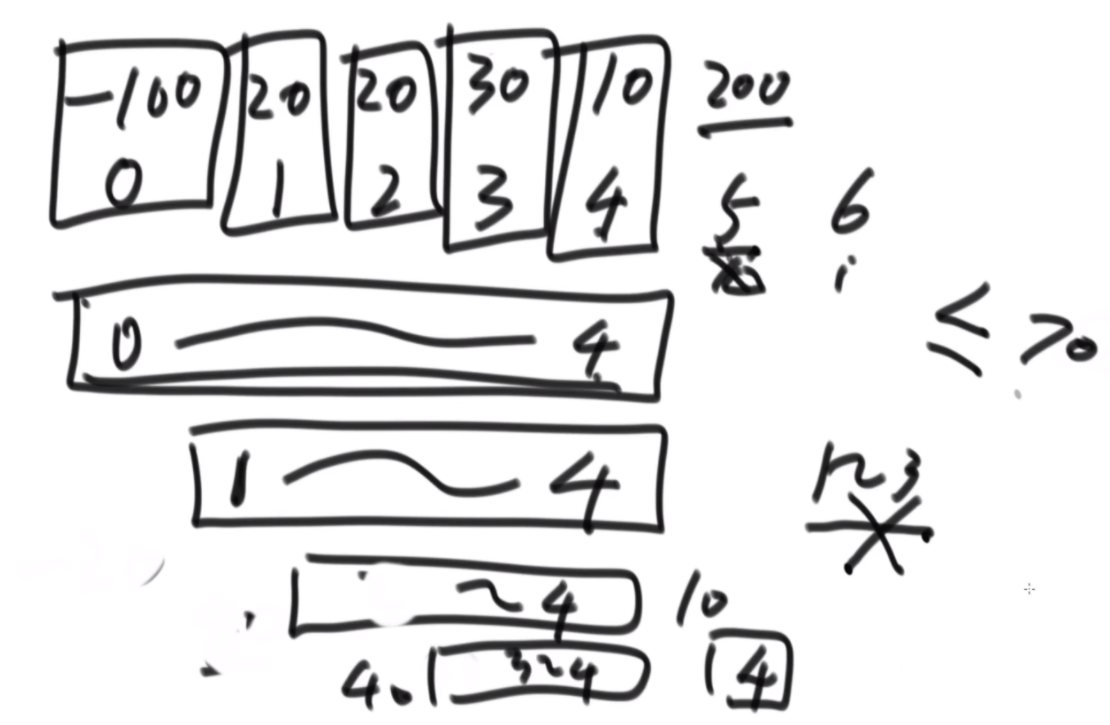
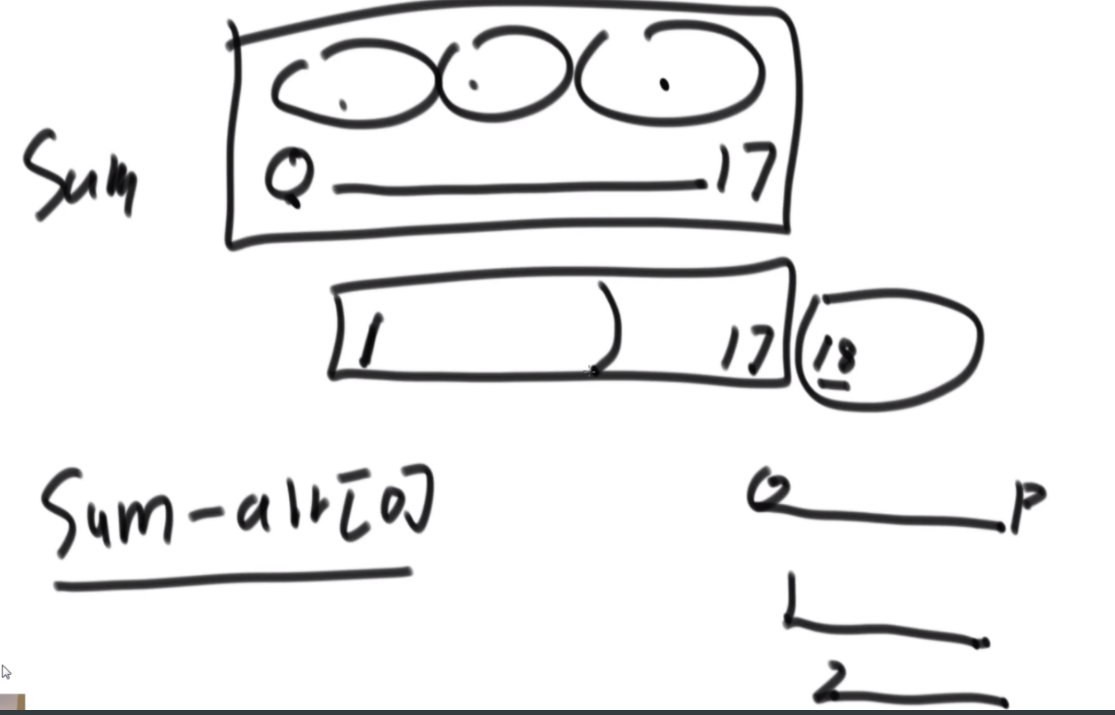
思路：（图一）首先搞一个minSum数组记录从i出发向右的子数组的最小和，minSumend记录这个最小和数组的结尾位置。（图二）这样的话从0位置开始的连续块数就可以快速完成当前位置的最大长度。（图三）实例，先从右往左开始生成这俩数组，如果右侧的值是负数就加上，如果是正数那么就不加。可以找到0位置当前的最小和结束位置是4.（图四）这里开始进入到算法的精髓部分，在判断完成0-4之后，用排除法减少可能性的方式去做，并不关心1位置开始的是啥情况，本来应该是1-3，但是因为已经有了0-4这个优秀解，直接去掉0节点，看1-4，能不能扩充5节点，不能，那么2-4，一直到4自己一个节点也不能扩充5节点，那么直接跳过5节点从6重新开始。（图五）这个算法的精髓就在于只关心最大的长度，而不关心单个的节点，只去试图加上下一个节点，一个个的删除最左侧的节点，这样就可以从左往右做到O(n)。

package class02;

public class Problem03_LongestLessSumSubArrayLength {

	public static int maxLengthAwesome(int[] arr, int k) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int[] minSums = new int[arr.length];
		int[] minSumEnds = new int[arr.length];
		minSums[arr.length - 1] = arr[arr.length - 1];
		minSumEnds[arr.length - 1] = arr.length - 1;
		for (int i = arr.length - 2; i >= 0; i--) {
			if (minSums[i + 1] < 0) {
				minSums[i] = arr[i] + minSums[i + 1];
				minSumEnds[i] = minSumEnds[i + 1];
			} else {
				minSums[i] = arr[i];
				minSumEnds[i] = i;
			}
		}
		int end = 0;
		int sum = 0;
		int res = 0;
		// i是窗口的最左的位置，end是窗口最右位置的下一个位置
		for (int i = 0; i < arr.length; i++) {
			// while循环结束之后：
			// 1) 如果以i开头的情况下，累加和<=k的最长子数组是arr[i..end-1]，看看这个子数组长度能不能更新res；
			// 2) 如果以i开头的情况下，累加和<=k的最长子数组比arr[i..end-1]短，更新还是不更新res都不会影响最终结果；
			while (end < arr.length && sum + minSums[end] <= k) {
				sum += minSums[end];
				end = minSumEnds[end] + 1;
			}
			res = Math.max(res, end - i);
			if (end > i) { // 窗口内还有数
				sum -= arr[i];
			} else { // 窗口内已经没有数了，说明从i开头的所有子数组累加和都不可能<=k
				end = i + 1;
			}
		}
		return res;
	}

	public static int maxLength(int[] arr, int k) {
		int[] h = new int[arr.length + 1];
		int sum = 0;
		h[0] = sum;
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			h[i + 1] = Math.max(sum, h[i]);
		}
		sum = 0;
		int res = 0;
		int pre = 0;
		int len = 0;
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			pre = getLessIndex(h, sum - k);
			len = pre == -1 ? 0 : i - pre + 1;
			res = Math.max(res, len);
		}
		return res;
	}

	public static int getLessIndex(int[] arr, int num) {
		int low = 0;
		int high = arr.length - 1;
		int mid = 0;
		int res = -1;
		while (low <= high) {
			mid = (low + high) / 2;
			if (arr[mid] >= num) {
				res = mid;
				high = mid - 1;
			} else {
				low = mid + 1;
			}
		}
		return res;
	}

	// for test
	public static int[] generateRandomArray(int len, int maxValue) {
		int[] res = new int[len];
		for (int i = 0; i != res.length; i++) {
			res[i] = (int) (Math.random() * maxValue) - (maxValue / 3);
		}
		return res;
	}

	public static void main(String[] args) {
		for (int i = 0; i < 10000000; i++) {
			int[] arr = generateRandomArray(10, 20);
			int k = (int) (Math.random() * 20) - 5;
			if (maxLengthAwesome(arr, k) != maxLength(arr, k)) {
				System.out.println("oops!");
			}
		}

	}
	
}

两个聪明人拿铜板看谁先拿完

给定一个非负数组，每一个值代表该位置上有几个铜板。a和b玩游戏，a先手，b后手，轮到某个人的时候，只能在一个位置上拿任意数量的铜板，但是不能不拿。谁最先把铜板拿完谁赢。假设a和b都极度聪明，请返回获胜者的名字。

思路：Nim博弈论，只要先手拿完铜板让剩余的所有数组位置上的铜板数量异或和为0，那么先手赢了。如果铜板的起始状况就是异或和为0，那么后手赢了。

package class02;

public class Problem04_Nim {

	// 保证arr是正数数组
	public static void printWinner(int[] arr) {
		int eor = 0;
		for (int num : arr) {
			eor ^= num;
		}
		if (eor == 0) {
			System.out.println("后手赢");
		} else {
			System.out.println("先手赢");
		}
	}

}

p31:

约瑟夫环（公司面试）优化

某公司招聘，有n个人入围，HR在黑板上依次写下m个正整数A1、A2、……、Am，然后让这n个人围成一个圈，并按照顺时针顺序为他们编号0、1、2、……、n-1。录取规则是：第一轮从0号的人开始，取用黑板上的第1个数字，也就是A1黑板上的数字按次序循环取用，即如果某轮用了第m个，则下一轮需要用第1个；如果某轮用到第k个，则下轮需要用第k+1个（k<m）

每一轮按照黑板上的次序取用到一个数字Ax，淘汰掉从当前轮到的人开始按照顺时针顺序数到的第Ax个人，下一轮开始时轮到的人即为被淘汰掉的人的顺时针顺序下一个人被淘汰的人直接回家，所以不会被后续轮次计数时数到经过n-1轮后，剩下的最后1人被录取所以最后被录取的人的编号与（n，m，A1，A2，……，Am）相关。

输入描述：第一行是一个正整数N，表示有N组参数从第二行开始，每行有若干个正整数，依次存放n、m、A1、……、Am，一共有N行，也就是上面的N组参数。

输出描述：输出有N行，每行对应相应的那组参数确定的录取之人的编号示例1:

输入

1

4 2 3 1

输出

1

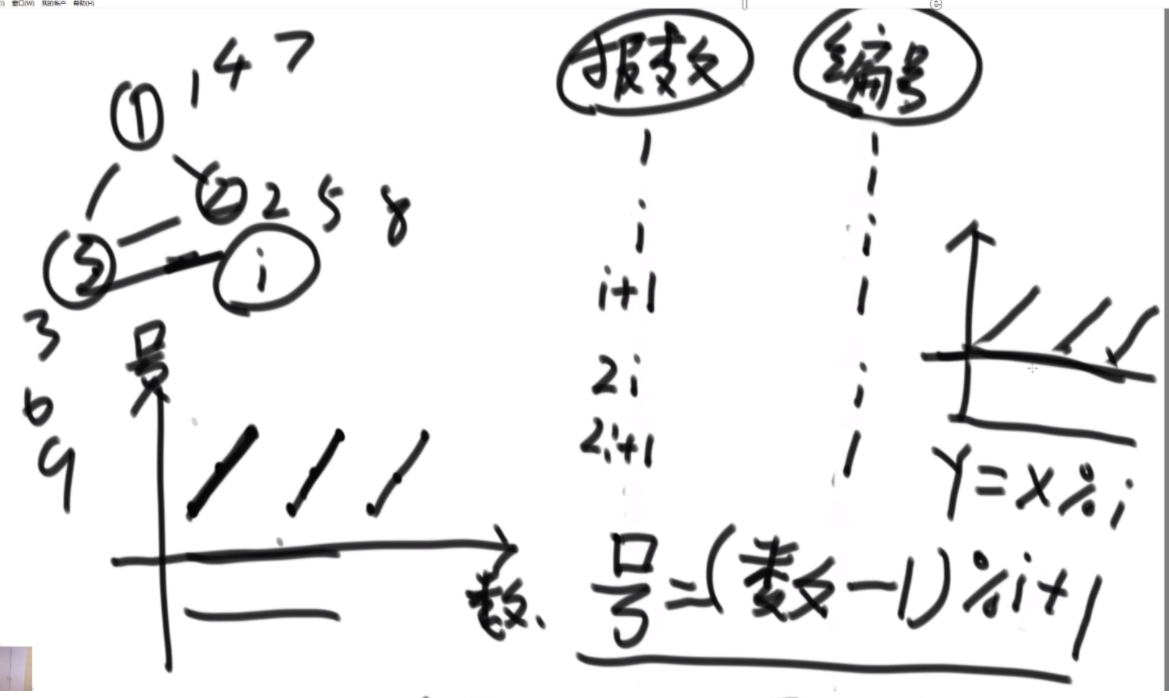
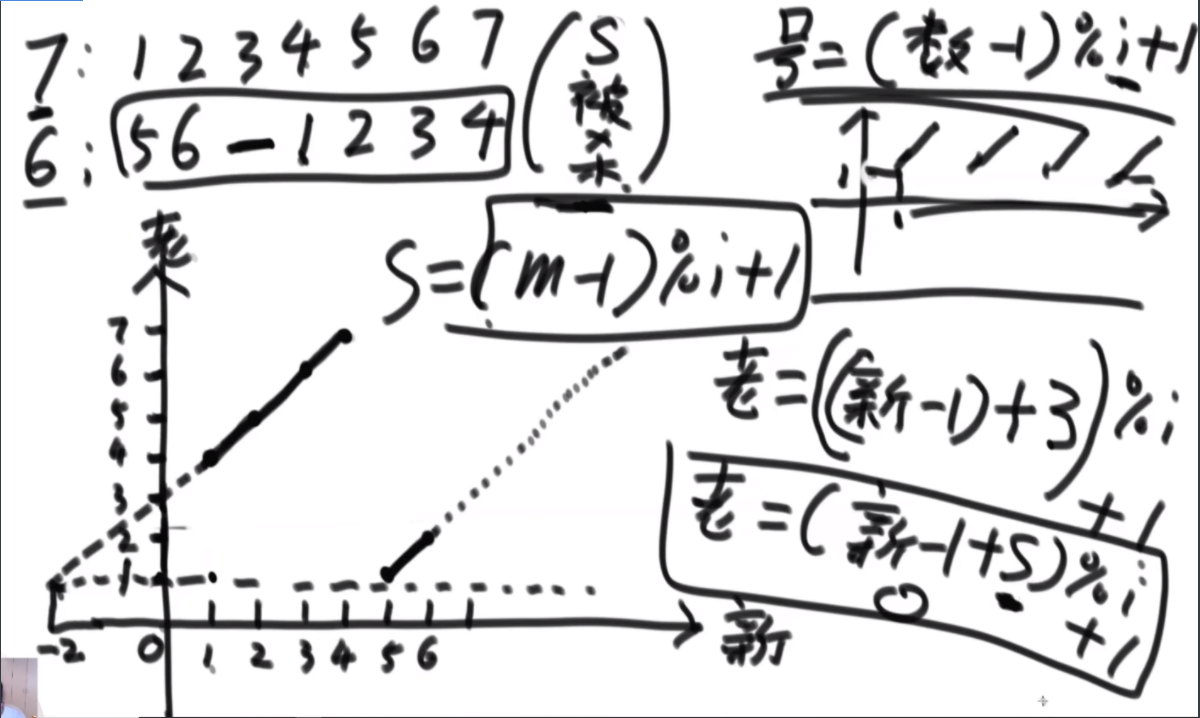
思路：首先解决约瑟夫环的优化问题，左上角通过报数和编号的规律，以及X%i的公式推导出编号和报数的关系。然后被杀后编号要更新，用新的编号套入，就可以得到老的结果，然后得到一次的公式。首先算出两个人的时候，数m次得到哪个或者的人的编号，然后套公式算3个人的，以此类推，O(1)的公式计算n次，时间复杂度为O(n)。

回归到这道题中，每个人数的m不一样，需要从数组中取得，完事。

public static Node josephusKill2(Node head, int m) {
		if (head == null || head.next == head || m < 1) {
			return head;
		}
		Node cur = head.next;
		int tmp = 1; // tmp -> list size
		while (cur != head) {
			tmp++;
			cur = cur.next;
		}
		tmp = getLive(tmp, m); // tmp -> service node position
		while (--tmp != 0) {
			head = head.next;
		}
		head.next = head;
		return head;
	}

	// 现在一共有i个节点，数到m就杀死节点，最终会活下来的节点，请返回它在i个节点时候的编号
	// 旧
	// getLive(N,m)
	public static int getLive(int i, int m) {
		if (i == 1) {
			return 1;
		}
		return (getLive(i - 1, m) + m - 1) % i + 1;
	}
	
	//这个题目的解：
	//0....n-1个人围成一圈，依次循环取用arr中的数字，
	//杀n-1轮，返回活的人的原始编号
	public static int live(int n,int[] arr){
		return no(n,arr,0)
	}
	
	//还剩i个人，当前取用数字是arr[index]，并且下面的过程，从index出发，循环取用
	//返回哪个人会活（i中的编号）
	public static int no(int i,int[] arr,int index){
		if(i==1){
			return 1;
		}
		//老 = (新+m-1)%i+1
		return (no(i-1,arr,nextIndex(arr.length,index) //新
				+arr[index]-1)%i
				+1;
	}
	//如果数组长度为size,当前下标为index，返回循环的模型下，下一个index是多少
	public static int nextIndex(int size,int index){
		return index == size-1?0:index+1;
	}

p29&p30:

排序之后相邻两数的最大差值

给定一个数组，求如果排序之后，相邻两数的最大差值。要求时间复杂度O(N)，且要求不能用非基于比较的排序。

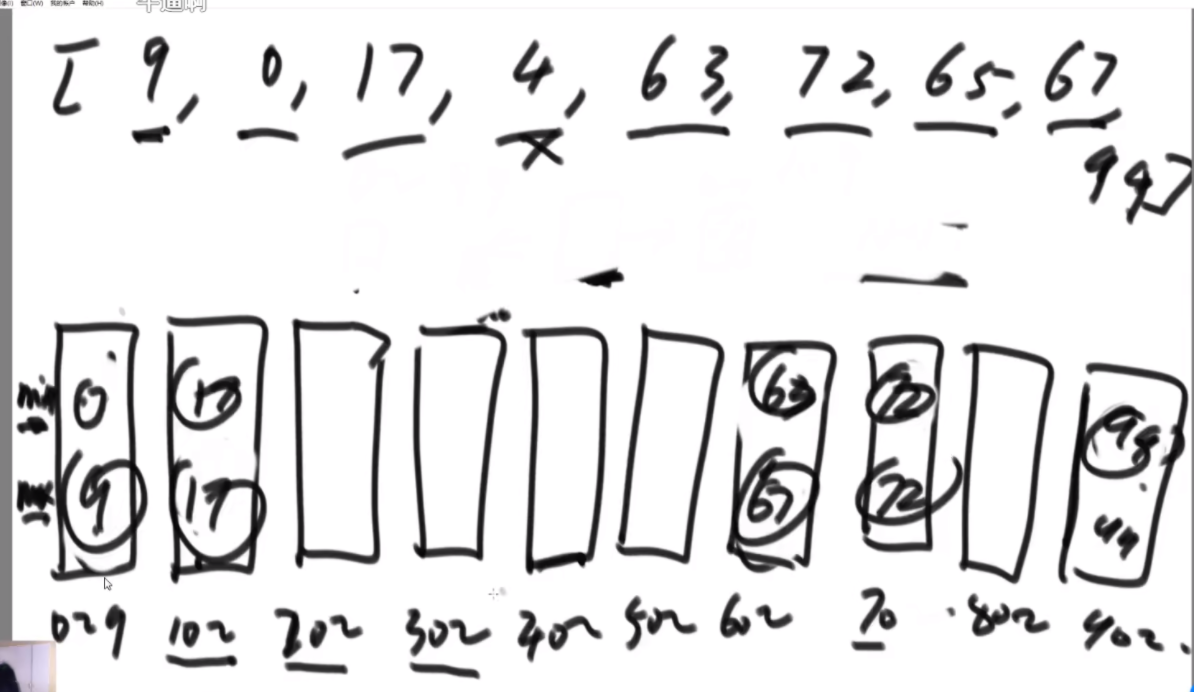
思路：这种贪心，是设置n+1个桶数量，人为构建了一种平凡解去优化流程，即一个桶之内是不可能为答案！因此只需要比较每个桶里的最小值或最大值和前一个桶之间的最小最大的差值即可。优化后为O(N)

package class01;

import java.util.Arrays;

public class Problem01_MaxGap {

	public static int maxGap(int[] nums) {
		if (nums == null || nums.length < 2) {
			return 0;
		}
		int len = nums.length;
		int min = Integer.MAX_VALUE;
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < len; i++) {
			min = Math.min(min, nums[i]);
			max = Math.max(max, nums[i]);
		}
		if (min == max) {
			return 0;
		}
		boolean[] hasNum = new boolean[len + 1]; //hasNum[i] i号桶是否进来过数字
		int[] maxs = new int[len + 1]; //maxs[i] i号桶收集的所有数字的最大值
		int[] mins = new int[len + 1]; //mins[i] i号桶收集的所有数字的最小值
		int bid = 0; //桶号
		for (int i = 0; i < len; i++) {
			bid = bucket(nums[i], len, min, max);
			mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i];
			maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i];
			hasNum[bid] = true;
		}
		int res = 0;
		int lastMax = maxs[0]; //上一个非空桶的最大值
		int i = 1;
		for (; i <= len; i++) {
			if (hasNum[i]) {
				res = Math.max(res, mins[i] - lastMax);
				lastMax = maxs[i];
			}
		}
		return res;
	}

	public static int bucket(long num, long len, long min, long max) {
		return (int) ((num - min) * len / (max - min));
	}

	// for test
	public static int comparator(int[] nums) {
		if (nums == null || nums.length < 2) {
			return 0;
		}
		Arrays.sort(nums);
		int gap = Integer.MIN_VALUE;
		for (int i = 1; i < nums.length; i++) {
			gap = Math.max(nums[i] - nums[i - 1], gap);
		}
		return gap;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			if (maxGap(arr1) != comparator(arr2)) {
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

划分区间让异或为0的区间最多

给出n个数字 a_1,...,a_n，问最多有多少不重叠的非空区间，使得每个区间内数字的xor都等于0。

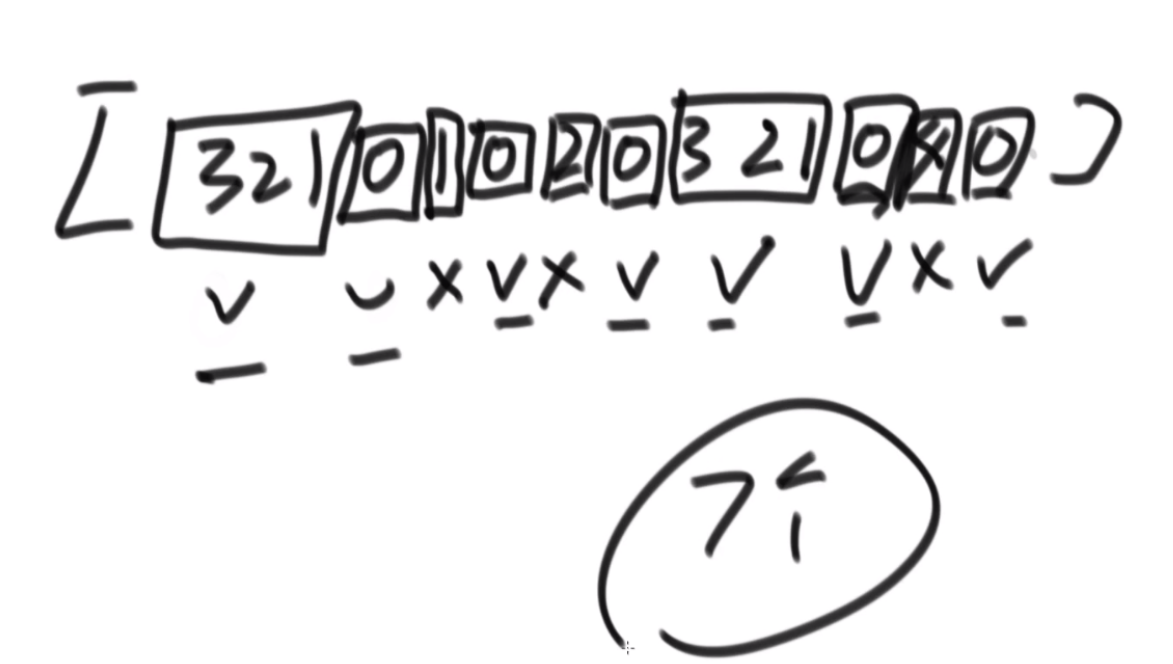
题目：有这么多分割方式，在这些分割方式中，能够让异或为0的小区间最多的划分方式。

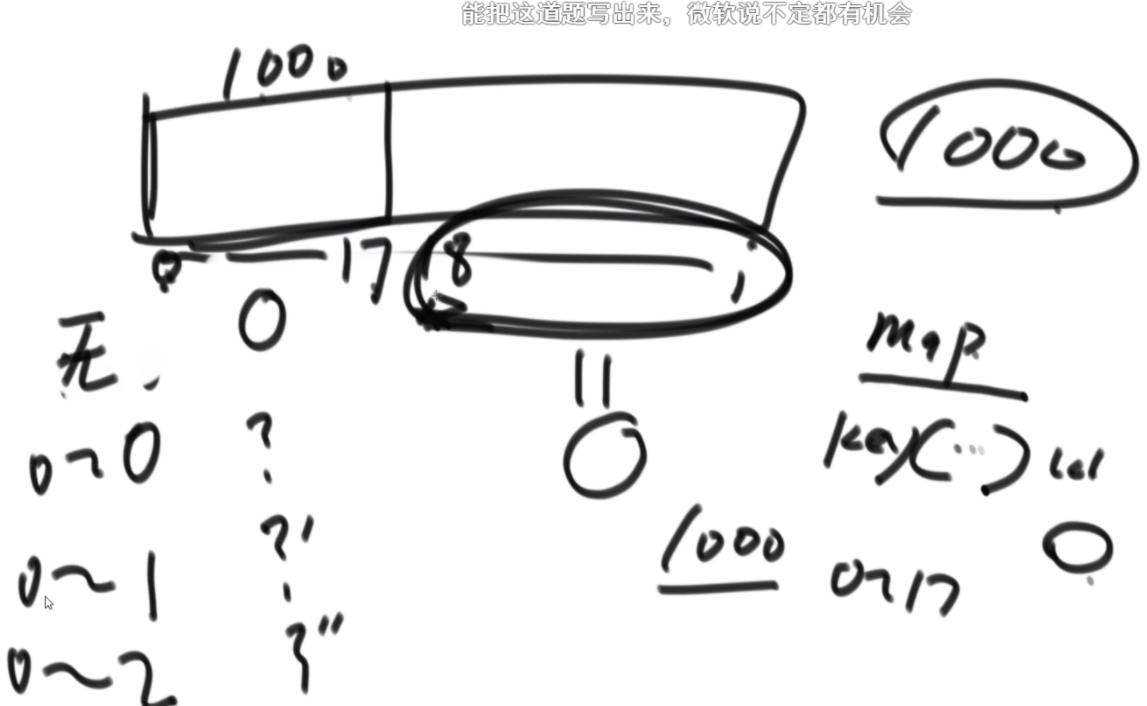
思路：搞一个dp数组，记录i位置，以i位置结尾的最佳的分割方式的结果。当然，每次分析只有两种可能，第一种是i位置不是异或为0，那么直接是前面的值，第二种是i位置是异或为0，那么+1。再整一个map，key是前缀异或和，value是最近出现的位置，如果0出现了两次，那么覆盖掉之前的位置，只保存最近的，其余的值也是。

package class01;

import java.util.HashMap;

public class Problem02_MostEOR {

	public static int mostEOR(int[] arr) {
		int ans = 0;
		int xor = 0;//dp[i]->arr[0..i]在最优划分的情况下，异或和为0最多的部分是多少个
		int[] mosts = new int[arr.length];
		//key:从0出发的某个前缀异或和
		//value：从这个前缀异或和出现的最晚(最近)的位置(index)
		HashMap<Integer, Integer> map = new HashMap<>();
		map.put(0, -1);//初始的时候异或值为0的位置为-1
		for (int i = 0; i < arr.length; i++) {// i所在的最后一块
			xor ^= arr[i]; //所有数的异或和
			if (map.containsKey(xor)) { //上一次这个异或和出现的位置
				//pre->pre+1->i,最优划分，最后一个位置的开始位置，
				//(pre+1,i)最后一个部分
				int pre = map.get(xor);//a 0..a (a+1..i)
				mosts[i] = pre == -1 ? 1 : (mosts[pre] + 1);
			}
			if (i > 0) {
				mosts[i] = Math.max(mosts[i - 1], mosts[i]);
			}
			map.put(xor, i);
			ans = Math.max(ans, mosts[i]);
		}
		return ans;
	}

	// for test
	public static int comparator(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int[] eors = new int[arr.length];
		int eor = 0;
		for (int i = 0; i < arr.length; i++) {
			eor ^= arr[i];
			eors[i] = eor;
		}
		int[] mosts = new int[arr.length];
		mosts[0] = arr[0] == 0 ? 1 : 0;
		for (int i = 1; i < arr.length; i++) {
			mosts[i] = eors[i] == 0 ? 1 : 0;
			for (int j = 0; j < i; j++) {
				if ((eors[i] ^ eors[j]) == 0) {
					mosts[i] = Math.max(mosts[i], mosts[j] + 1);
				}
			}
			mosts[i] = Math.max(mosts[i], mosts[i - 1]);
		}
		return mosts[mosts.length - 1];
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random());
		}
		return arr;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 300;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			int res = mostEOR(arr);
			int comp = comparator(arr);
			if (res != comp) {
				succeed = false;
				printArray(arr);
				System.out.println(res);
				System.out.println(comp);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

n张普通币和数张纪念币拼面值

现有n1+n2种面值的硬币，其中前n1种为普通币，可以取任意枚，后n2种为纪念币，每种最多只能取一枚，每种硬币有一个面值，问能用多少种方法拼出m的面值？

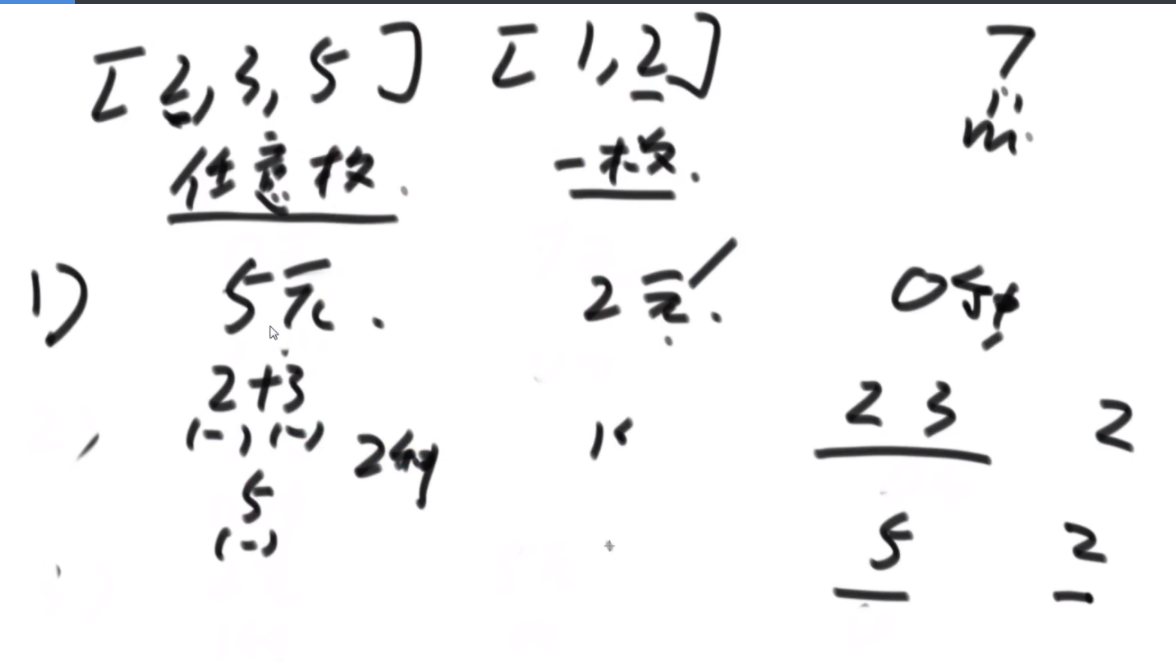
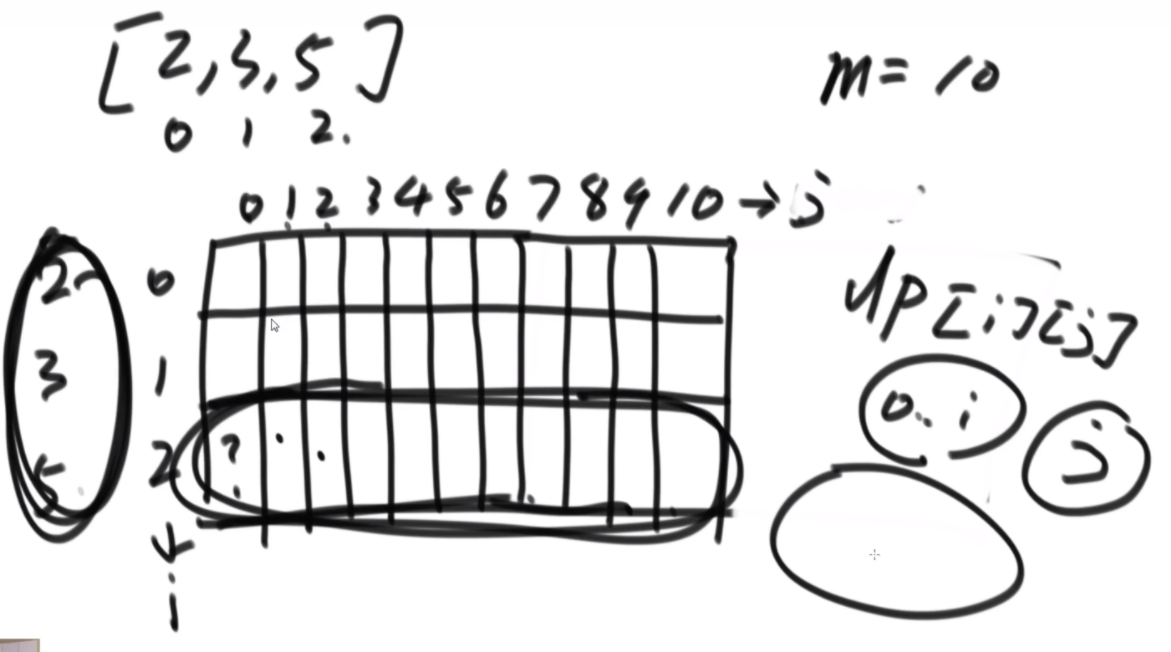
思路：类似于背包问题，两个动态规划。首先将方法数分解成左边乘以右边，左右两边的生成过程各自是一个动态规划。普通币的dp还用到了斜率优化，需要自己去翻，有心情的时候再搞吧。好吧他又讲了，看下面的图：

这个图讲得是可以使用任意张数的币。这里左边是钱币的面值和数组位置，（0，3）代表用3面值的钱表示3块钱有几种方法，（1，8）代表用任意数量的3块和2块的币去表示8块钱，首先是看8块全部用3块的表示，即（0，8）位置，然后是6块全用3表示，然后是4块，依次相加，一直加到（0，0），这就是（1，8），因为这里有枚举行为，因此在计算（1，6）的时候就是（1，8）-（0，8），这种减少遍历的方式是斜率优化，用附近的格子去求，而不是枚举。纪念币因为是只能用1张，因此没有枚举行为，不需要斜率优化。

package class01;

public class Problem03_MoneyWays {

	public static int moneyWays(int[] arbitrary, int[] onlyone, int money) {
		if (money < 0) {
			return 0;
		}
		if ((arbitrary == null || arbitrary.length == 0)
				&& (onlyone == null || onlyone.length == 0)) {
			return money == 0 ? 1 : 0;
		}
		int[][] dparb = getDpArb(arbitrary, money);
		int[][] dpone = getDpOne(onlyone, money);
		if (dparb == null) {
			return dpone[dpone.length - 1][money];
		}
		if (dpone == null) {
			return dparb[dparb.length - 1][money];
		}
		int res = 0;
		for (int i = 0; i <= money; i++) {
			res += dparb[dparb.length - 1][i]
					* dpone[dpone.length - 1][money - i];
		}
		return res;
	}

	public static int[][] getDpArb(int[] arr, int money) {
		if (arr == null || arr.length == 0) {
			return null;
		}
		int[][] dp = new int[arr.length][money + 1];
		for (int i = 0; i < arr.length; i++) {
			dp[i][0] = 1;
		}
		for (int j = 1; arr[0] * j <= money; j++) {
			dp[0][arr[0] * j] = 1;
		}
		for (int i = 1; i < arr.length; i++) {
			for (int j = 1; j <= money; j++) {
				dp[i][j] = dp[i - 1][j];
				dp[i][j] += j - arr[i] >= 0 ? dp[i][j - arr[i]] : 0;
			}
		}
		return dp;
	}

	public static int[][] getDpOne(int[] arr, int money) {
		if (arr == null || arr.length == 0) {
			return null;
		}
		int[][] dp = new int[arr.length][money + 1];
		for (int i = 0; i < arr.length; i++) {
			dp[i][0] = 1;
		}
		if (arr[0] <= money) {
			dp[0][arr[0]] = 1;
		}
		for (int i = 1; i < arr.length; i++) {
			for (int j = 1; j <= money; j++) {
				dp[i][j] = dp[i - 1][j];
				dp[i][j] += j - arr[i] >= 0 ? dp[i - 1][j - arr[i]] : 0;
			}
		}
		return dp;
	}

}

找出最大的k个数字

给定两个一维int数组A和B.其中：A是长度为m、元素从小到大排好序的有序数组。B是长度为n、元素从小到大排好序的有序数组。希望从A和B数组中，找出最大的k个数字，要求：使用尽量少的比较次数。

方法一：搞两个指针，A小就A指针走，B小就B指针走，一直走K个，找到第K大。

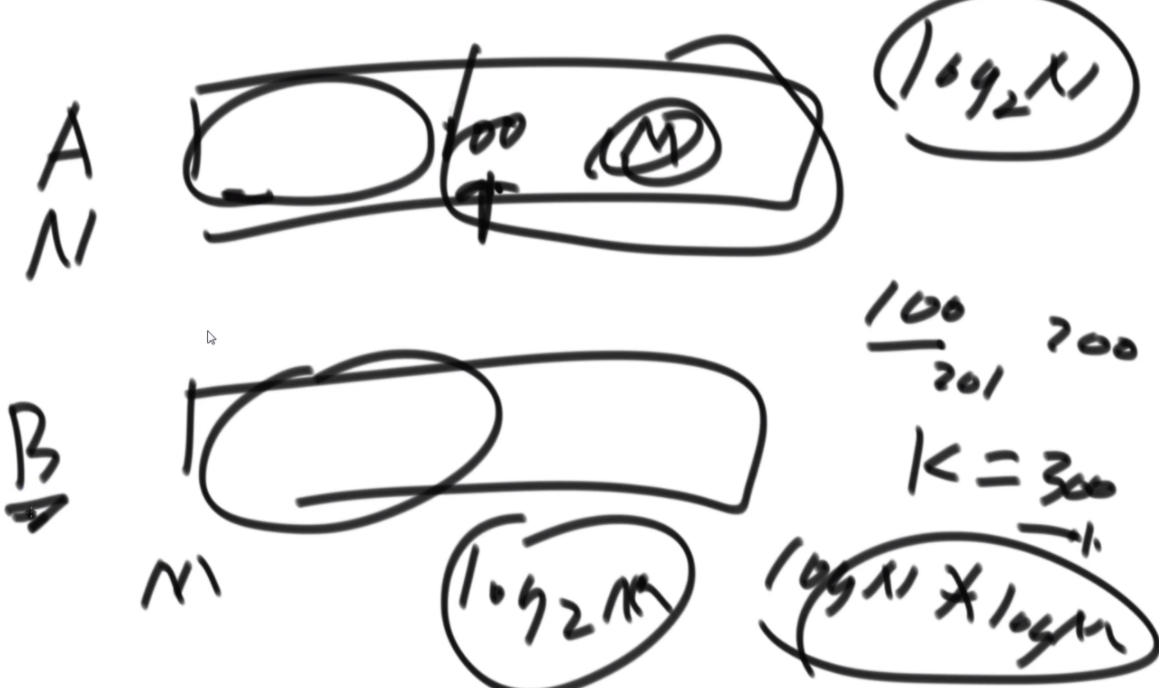
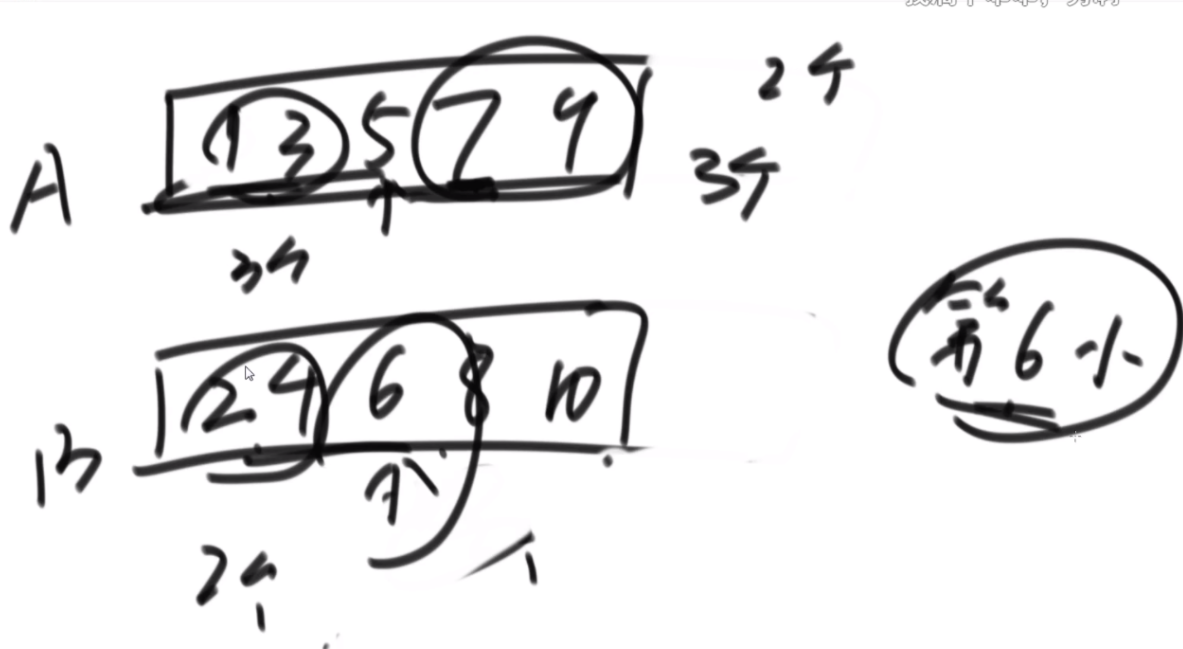
方法二：去二分的找，比如在A中找到二分位置的数5，那么就可以得知5大于2个数，然后去B中找比5大的第一个数，也是二分找，找到6，前面有2个，因此6是6大的数。

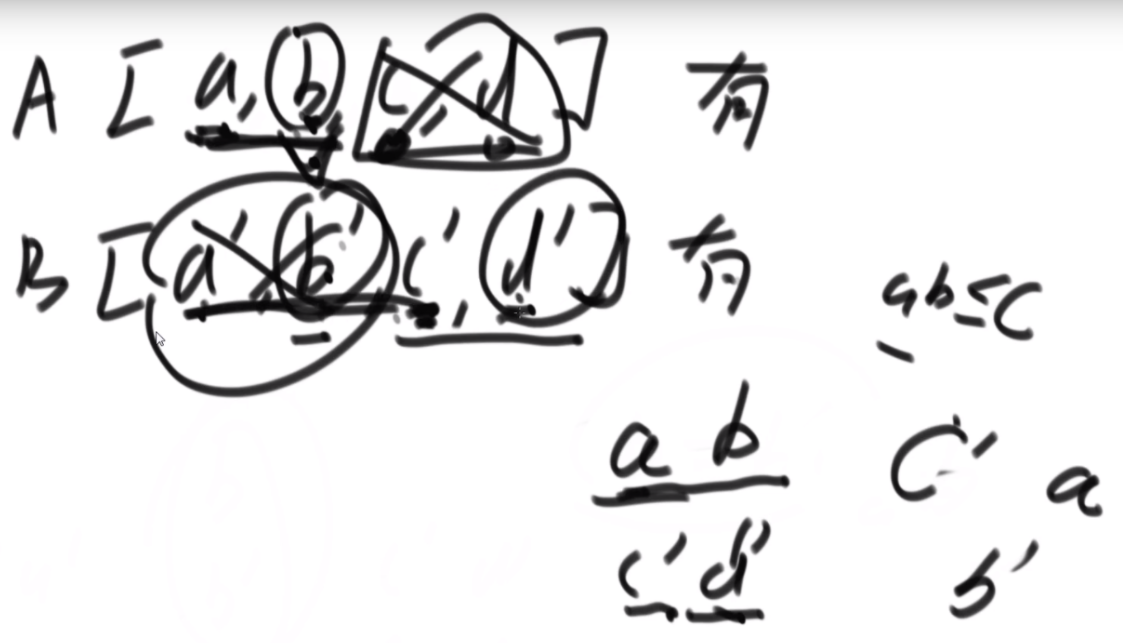
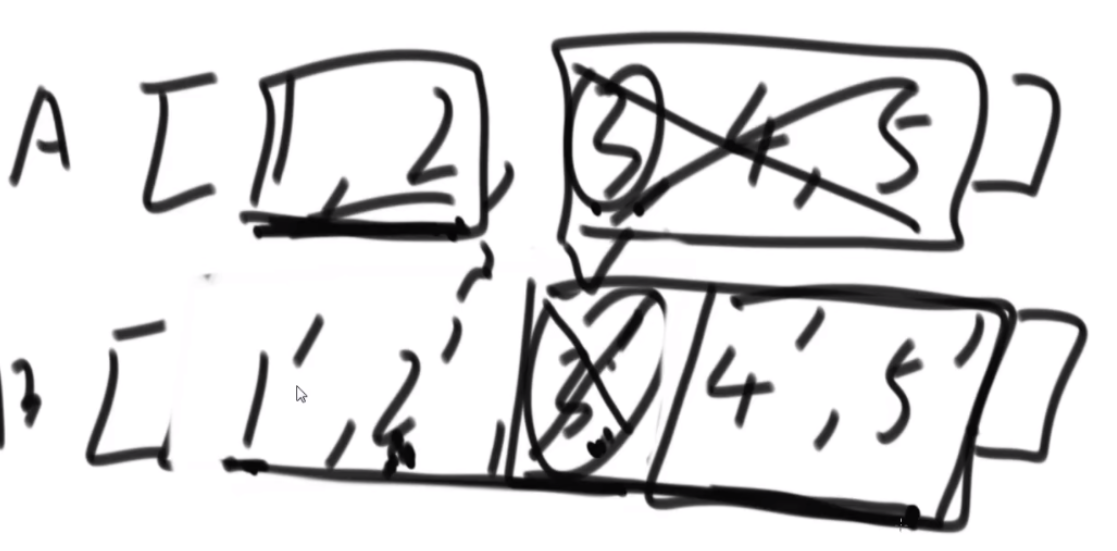
方法三：（左神自己的解法最优）：递归找到的上中位数就是整体的上中位数

算法原型：当两个有序的等长数组的上中位数

当这个数组的长度为偶数时，去找A中的前中位数b（中位数中靠前的那个），然后找到B中的前中位数b'，如果b>b'，那么可以排除掉b后面的以及c'前面的，归结为A的前半部分和B的后半部分两个长度相等的小数组去递归这个操作。

当这个数组的长度为奇数时，需要手动的去把中间那个数去去掉，当3>3'的时候，且3'<2，那么第5小的数一定在A的前半部分和B的后半部分然后继续递归。

那么如何去解这道题呢？需要分成3种情况，假设A长度为10，B长度为17

1. K<=10，那么直接取A的全部和B的前10个套算法原型

2. 10<K<=17，那么需要去手动去除一些数字，如下图中，假设K是15，那么B中的前五个可以去掉，最后两个也可以去掉，中间的正好是10个，和A数组相同，如果长度不同可以通过和A中的10去比较大小来排除。

   

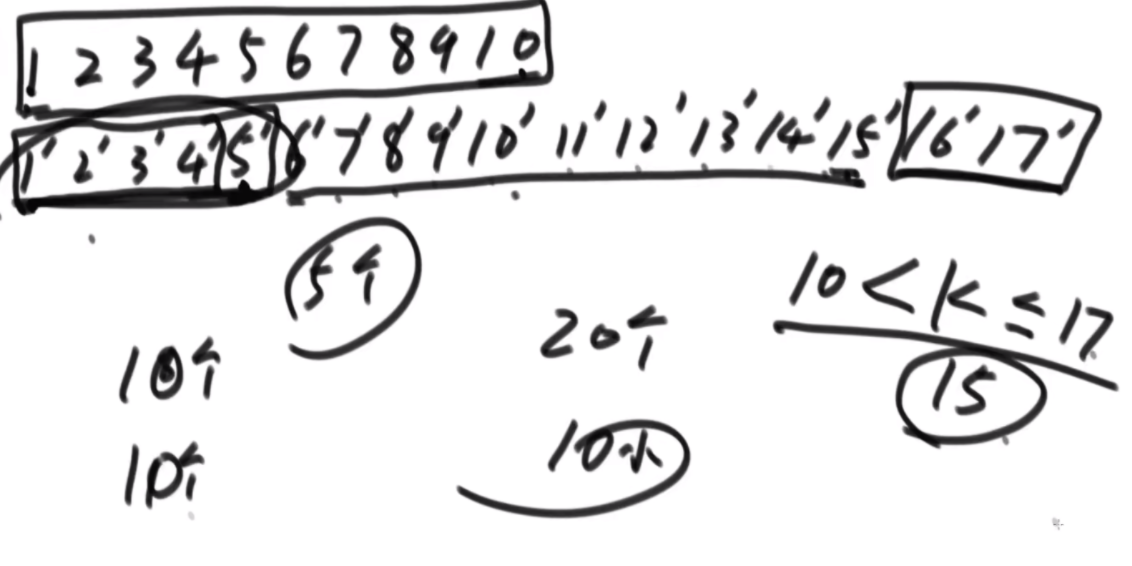
3. 17<K<=27，那么需要去手动去除一些数字，如下图中，假设K=23，首先A数组中前5个是没有可能的，因为就算6>17'也不能是第23大的，因此A是7-10有可能，B中同理，就算12'大于10也是最多第22大，因此B可能是13'-17'，这里两个中长度不一致，因此需要判断一下13'和10的大小，如果比10大，那么就是13'，如果不是的话就可以排除13'，那么两个数组长度一致后可以去套算法模型。

   

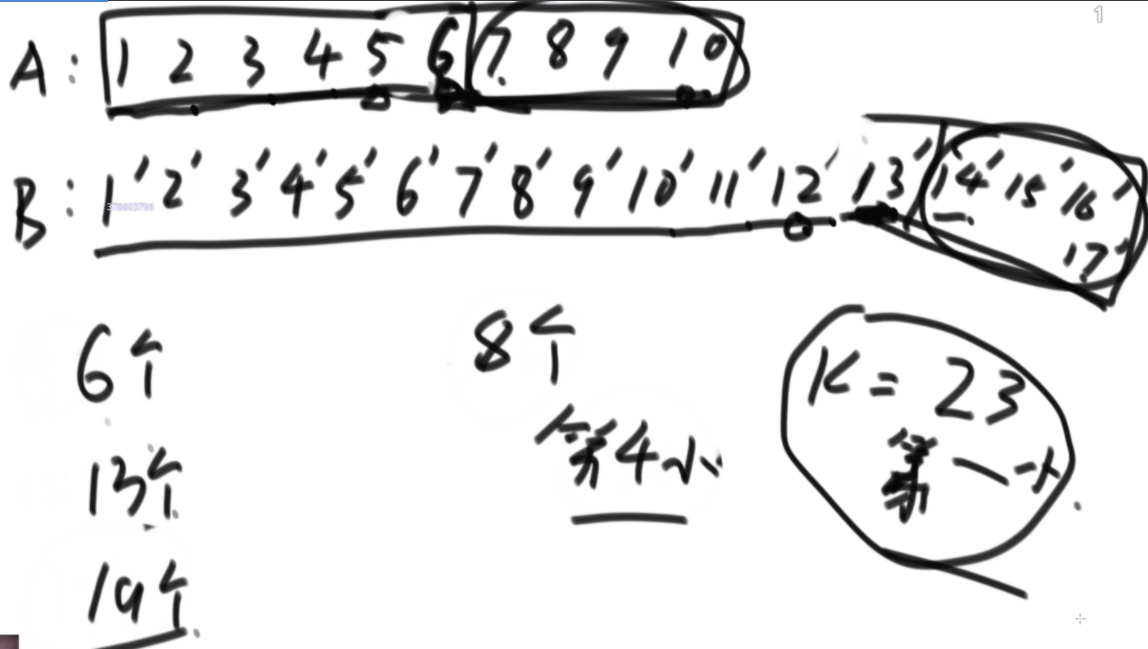
时间复杂度：O(log{min(N,M)})

package class01;

import java.util.Arrays;

public class Problem05_FindKthMinNumber {

	public static int findKthNum(int[] arr1, int[] arr2, int kth) {
		if (arr1 == null || arr2 == null) {
			throw new RuntimeException("Your arr is invalid!");
		}
		if (kth < 1 || kth > arr1.length + arr2.length) {
			throw new RuntimeException("K is invalid!");
		}
		int[] longs = arr1.length >= arr2.length ? arr1 : arr2;
		int[] shorts = arr1.length < arr2.length ? arr1 : arr2;
		int l = longs.length;
		int s = shorts.length;
		if (kth <= s) {
			return getUpMedian(shorts, 0, kth - 1, longs, 0, kth - 1);
		}
		if (kth > l) {
			if (shorts[kth - l - 1] >= longs[l - 1]) {
				return shorts[kth - l - 1];
			}
			if (longs[kth - s - 1] >= shorts[s - 1]) {
				return longs[kth - s - 1];
			}
			return getUpMedian(shorts, kth - l, s - 1, longs, kth - s, l - 1);
		}
		if (longs[kth - s - 1] >= shorts[s - 1]) {
			return longs[kth - s - 1];
		}
		return getUpMedian(shorts, 0, s - 1, longs, kth - s, kth - 1);
	}

	public static int getUpMedian(int[] a1, int s1, int e1, int[] a2, int s2,
			int e2) {
		int mid1 = 0;
		int mid2 = 0;
		int offset = 0;
		while (s1 < e1) {
			mid1 = (s1 + e1) / 2;
			mid2 = (s2 + e2) / 2;
			offset = ((e1 - s1 + 1) & 1) ^ 1;
			if (a1[mid1] > a2[mid2]) {
				e1 = mid1;
				s2 = mid2 + offset;
			} else if (a1[mid1] < a2[mid2]) {
				s1 = mid1 + offset;
				e2 = mid2;
			} else {
				return a1[mid1];
			}
		}
		return Math.min(a1[s1], a2[s2]);
	}

	// For test, this method is inefficient but absolutely right
	public static int[] getSortedAllArray(int[] arr1, int[] arr2) {
		if (arr1 == null || arr2 == null) {
			throw new RuntimeException("Your arr is invalid!");
		}
		int[] arrAll = new int[arr1.length + arr2.length];
		int index = 0;
		for (int i = 0; i != arr1.length; i++) {
			arrAll[index++] = arr1[i];
		}
		for (int i = 0; i != arr2.length; i++) {
			arrAll[index++] = arr2[i];
		}
		Arrays.sort(arrAll);
		return arrAll;
	}

	public static int[] generateSortedArray(int len, int maxValue) {
		int[] res = new int[len];
		for (int i = 0; i != len; i++) {
			res[i] = (int) (Math.random() * (maxValue + 1));
		}
		Arrays.sort(res);
		return res;
	}

	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int len1 = 10;
		int len2 = 23;
		int maxValue1 = 20;
		int maxValue2 = 100;
		int[] arr1 = generateSortedArray(len1, maxValue1);
		int[] arr2 = generateSortedArray(len2, maxValue2);
		printArray(arr1);
		printArray(arr2);
		int[] sortedAll = getSortedAllArray(arr1, arr2);
		printArray(sortedAll);
		int kth = 17;
		System.out.println(findKthNum(arr1, arr2, kth));
		System.out.println(sortedAll[kth - 1]);

	}

}

p27&p28:

找到1-n中未出现的数

给定一个整数数组A，长度为n，有 1 <= A[i] <= n，且对于[1,n]的整数，其中部分整数会重复出现而部分不会出现。实现算法找到[1,n]中所有未出现在A中的整数。

提示：尝试实现O(n)的时间复杂度和O(1)的空间复杂度（返回值不计入空间复杂度）。

输入描述：一行数字，全部为整数，空格分隔A0 A1 A2 A3...

输出描述：一行数字，全部为整数，空格分隔R0 R1 R2 R3...

示例1: 输入1 3 4 3

输出 2

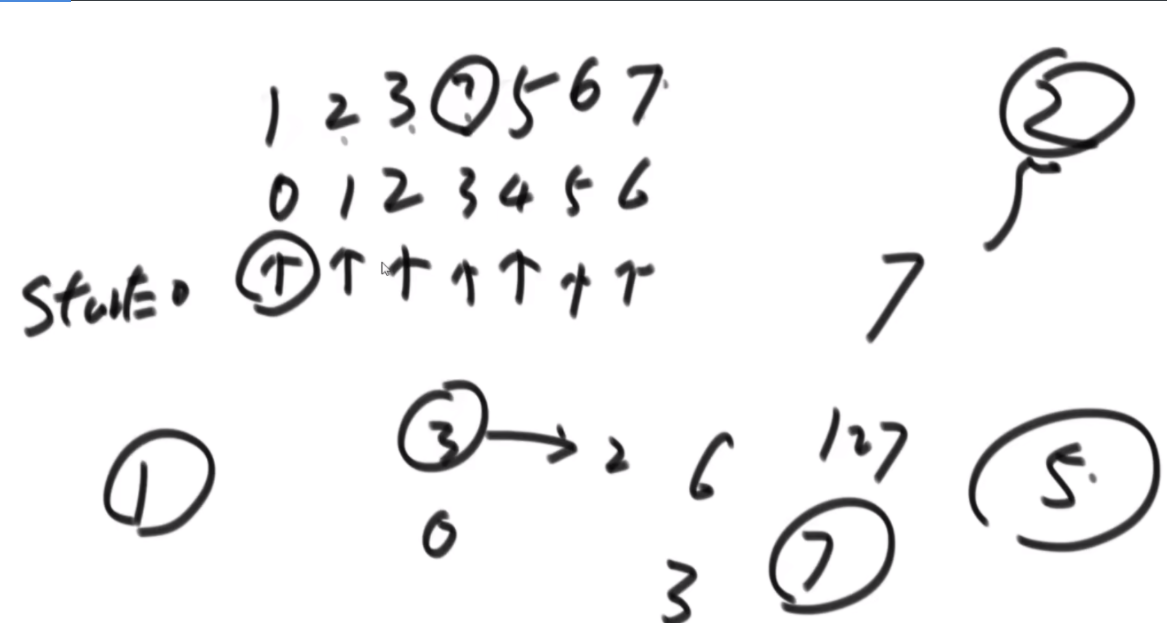
思路：让i位置上的数字为i+1，从0位置出发，挨个放，回到初始位置的时候往下走或者值重复了往下走，走到1，依次走到头。最后遍历一遍，发现3位置上少一个。

package class07;

public class Problem02_PrintNoInArray {

	// 请保证arr[0..N-1]上的数字都在[1～n]之间
	public static void printNumberNoInArray(int[] arr) {
		if (arr == null || arr.length == 0) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {//争取做到，i位置上，放的数是i+1
			modify(arr[i], arr);
		}
		for (int i = 0; i < arr.length; i++) {
			if (arr[i] != i + 1) { //没做到的位置，就知道缺了
				System.out.println(i + 1);
			}
		}
	}
	//每次一直做到i位置上是i+1
	public static void modify(int value, int[] arr) {
		while (arr[value - 1] != value) {
			int tmp = arr[value - 1];
			arr[value - 1] = value;
			value = tmp;
		}
	}

	public static void main(String[] args) {
		int[] test = { 3, 2, 3, 5, 6, 1, 6 };
		printNumberNoInArray(test);
	}

}

主播打赏计算

CC里面有一个土豪很喜欢一位女直播Kiki唱歌，平时就经常给她点赞、送礼、私聊。最近CC直播平台在举行 中秋之星主播唱歌比赛，假设一开始该女主播的初始人气值为start， 能够晋升下一轮人气需要刚好达到end， 土豪给主播增加人气的可以采取的方法有：

a.点赞 花费x C币，人气 + 2

b.送礼 花费y C币，人气 * 2

c.私聊 花费z C币，人气 - 2

其中 end 远大于start且end为偶数， 请写一个程序帮助土豪计算一下，最少花费多少C币就能帮助该主播Kiki将人气刚好达到end，从而能够晋级下一轮？

输入描述：第一行输入5个数据，分别为：x y z start end，每项数据以空格分开。其中：0＜x, y, z＜＝10000， 0＜start, end＜＝1000000

输出描述：需要花费的最少C币。

示例1: 输入3 100 1 2 6

输出 6

思路：假如是正常的递归，会发现没有停止条件。限制条件1：这个时候需要去搞一个平凡解，只要花费的钱数大于平凡解的钱数就停止。限制条件2：花费的钱数不会大于2倍的b。根据abc三种方式的业务决定。

package class07;

public class Problem04_Kiki {

	//start偶数，end偶数  start<=end
	public static int minCcoins1(int add, int times, int del, int start, int end) {
		if (start > end) {
			return -1;
		}
		return process(0, end, add, times, del, start, end * 2, ((end - start) / 2) * add);
	}

	// pre之前已经花了多少钱  可变
	// aim目标  固定
	// int add int times int del  固定  x,y,z
	// finish 当前来到的人气
	// limitAim 人气大到什么程度不需要再尝试了  固定
	// limitCoin 已经使用的币大到什么程度不需要再尝试了 固定
	public static int process(int pre, int aim, int add, int times, int del, 
	int finish, int limitAim, int limitCoin) {
		if (pre > limitCoin) {
			return Integer.MAX_VALUE;
		}
		if (aim < 0) {
			return Integer.MAX_VALUE;
		}
		if (aim > limitAim) {
			return Integer.MAX_VALUE;
		}
		if (aim == finish) {
			return pre;
		}
		int min = Integer.MAX_VALUE;
		//让人气-2的方式
		int p1 = process(pre + add, aim - 2, add, times, del, finish, limitAim, limitCoin);
		if (p1 != Integer.MAX_VALUE) {
			min = p1;
		}
		//让人气+2的方式
		int p2 = process(pre + del, aim + 2, add, times, del, finish, limitAim, limitCoin);
		if (p2 != Integer.MAX_VALUE) {
			min = Math.min(min, p2);
		}
		if ((aim & 1) == 0) {
			//让人气*2的方式
			int p3 = process(pre + times, aim * 2, add, times, del, finish, limitAim, limitCoin);
			if (p3 != Integer.MAX_VALUE) {
				min = Math.min(min, p3);
			}
		}
		return min;
	}

	public static int minCcoins2(int add, int times, int del, int start, int end) {
		if (start > end) {
			return -1;
		}
		int limitCoin = ((end - start) / 2) * add;
		int limitAim = end * 2;
		int[][] dp = new int[limitCoin + 1][limitAim + 1];
		for (int pre = 0; pre <= limitCoin; pre++) {
			for (int aim = 0; aim <= limitAim; aim++) {
				if (aim == start) {
					dp[pre][aim] = pre;
				} else {
					dp[pre][aim] = Integer.MAX_VALUE;
				}
			}
		}
		for (int pre = limitCoin; pre >= 0; pre--) {
			for (int aim = 0; aim <= limitAim; aim++) {
				if (aim - 2 >= 0 && pre + add <= limitCoin) {
					dp[pre][aim] = Math.min(dp[pre][aim], dp[pre + add][aim - 2]);
				}
				if (aim + 2 <= limitAim && pre + del <= limitCoin) {
					dp[pre][aim] = Math.min(dp[pre][aim], dp[pre + del][aim + 2]);
				}
				if ((aim & 1) == 0) {
					if (aim / 2 >= 0 && pre + times <= limitCoin) {
						dp[pre][aim] = Math.min(dp[pre][aim], dp[pre + times][aim / 2]);
					}
				}
			}
		}
		return dp[0][end];
	}

	public static void main(String[] args) {
		int add = 6;
		int times = 5;
		int del = 1;
		int start = 10;
		int end = 30;
		System.out.println(minCcoins1(add, times, del, start, end));
		System.out.println(minCcoins2(add, times, del, start, end));
	}

}

主播参加活动的最大奖励

CC直播的运营部门组织了很多运营活动，每个活动需要花费一定的时间参与，主播每参加完一个活动即可得到一定的奖励，参与活动可以从任意活动开始，但一旦开始，就需要将后续活动参加完毕（注意：最后一个活动必须参与），活动之间存在一定的依赖关系（不存在环的情况），现在给出所有的活动时间与依赖关系，以及给出有限的时间，请帮主播计算在有限的时候内，能获得的最大奖励，以及需要的最少时长。

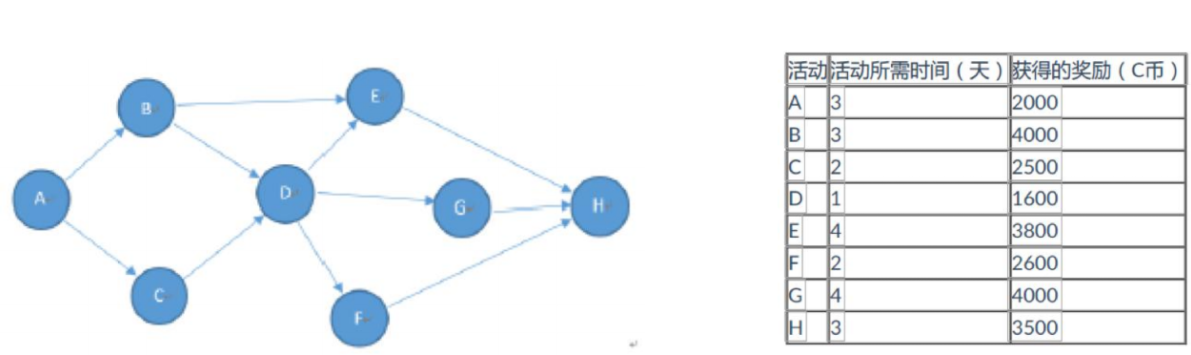
如上图数据所示，给定有限时间为10天。可以获取得最大奖励为：11700，需要的时长为：9天。参加的活动为BDFH四个。

输入描述：第一行输入数据N与D，表示有N项活动，D表示给予的时长。0＜N＜＝1000，0＜D＜＝10000。从第二行开始到N+1行，每行描述一个活动的信息，其中第一项表示当前活动需要花费的时间t，第二项表示可以获得的奖励a，之后有N项数据，表示当前活动与其他活动的依赖关系，1表示有依赖，0表示无依赖。每项数据用空格分开。

输出描述：输出两项数据A与T，用空格分割。A表示所获得的最大奖励，T表示所需要的时长。

输入

8 10

3 2000 0 1 1 0 0 0 0 0

3 4000 0 0 0 1 1 0 0 0

2 2500 0 0 0 1 0 0 0 0

1 1600 0 0 0 0 1 1 1 0

4 3800 0 0 0 0 0 0 0 1

2 2600 0 0 0 0 0 0 0 1

4 4000 0 0 0 0 0 0 0 1

3 3500 0 0 0 0 0 0 0 0

输出

11700 9

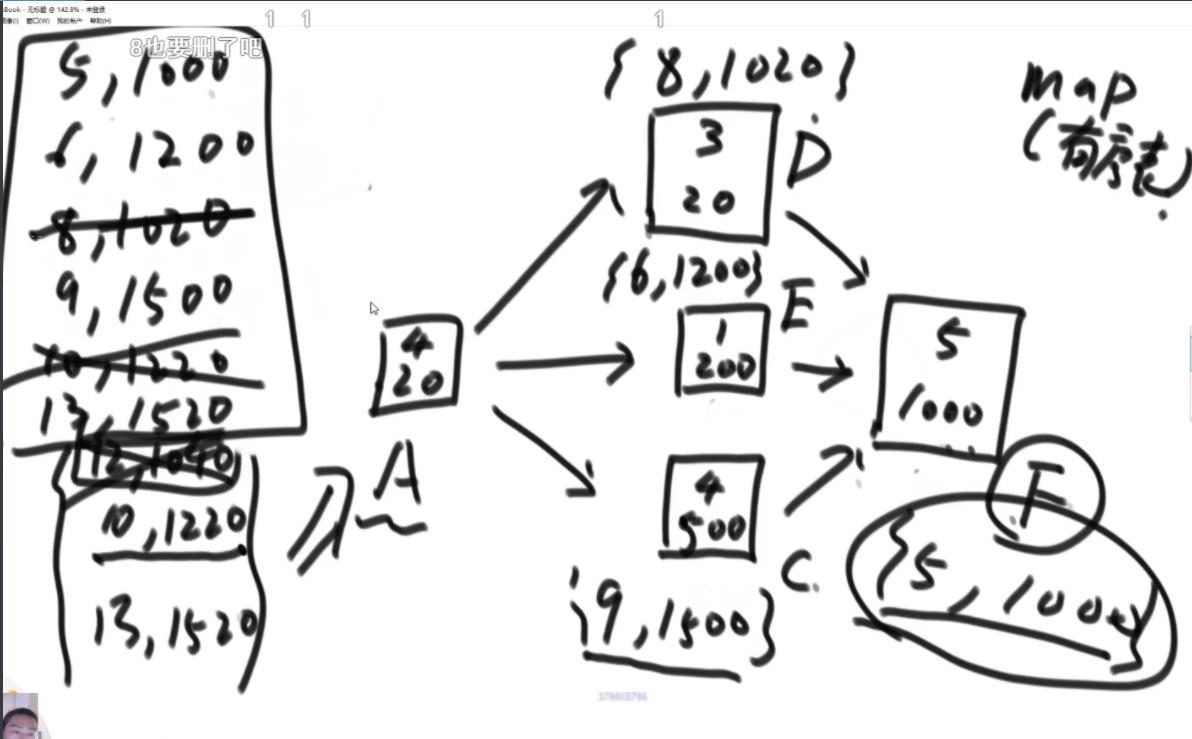
思路：倒着的广度优先遍历，从结尾出发，生成节点，然后每往回走都生成节点，然后汇总的时候，比如A节点，会搞一个有序表，内部逻辑是天数增加的时候，报酬一定增加，删掉多余的，最后把所有的合在一起，遍历一遍完事。节点内洗自己的，总表再洗一次，是因为怕节点之间的联系丢失。

package class07;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Map.Entry;
import java.util.TreeMap;

public class Problem06_MaxRevenue {

	// 请保证只有唯一的最后节点
	public static int[] maxRevenue(int allTime, int[] revenue, int[] times, int[][] dependents) {
		int size = revenue.length;
		HashMap<Integer, ArrayList<Integer>> parents = new HashMap<>();
		for (int i = 0; i < size; i++) {
			parents.put(i, new ArrayList<>());
		}
		int end = -1;
		for (int i = 0; i < dependents.length; i++) {
			boolean allZero = true;
			for (int j = 0; j < dependents[0].length; j++) {
				if (dependents[i][j] != 0) {
					parents.get(j).add(i);
					allZero = false;
				}
			}
			if (allZero) {
				end = i;
			}
		}
		HashMap<Integer, TreeMap<Integer, Integer>> nodeCostRevenueMap = new HashMap<>();
		for (int i = 0; i < size; i++) {
			nodeCostRevenueMap.put(i, new TreeMap<>());
		}
		nodeCostRevenueMap.get(end).put(times[end], revenue[end]);
		LinkedList<Integer> queue = new LinkedList<>();
		queue.add(end);
		while (!queue.isEmpty()) {
			int cur = queue.poll();
			for (int last : parents.get(cur)) {
				for (Entry<Integer, Integer> entry : nodeCostRevenueMap.get(cur).entrySet()) {
					int lastCost = entry.getKey() + times[last];
					int lastRevenue = entry.getValue() + revenue[last];
					TreeMap<Integer, Integer> lastMap = nodeCostRevenueMap.get(last);
					if (lastMap.floorKey(lastCost) == null || lastMap.get(lastMap.floorKey(lastCost)) < lastRevenue) {
						lastMap.put(lastCost, lastRevenue);
					}
				}
				queue.add(last);
			}
		}
		TreeMap<Integer, Integer> allMap = new TreeMap<>();
		for (TreeMap<Integer, Integer> curMap : nodeCostRevenueMap.values()) {
			for (Entry<Integer, Integer> entry : curMap.entrySet()) {
				int cost = entry.getKey();
				int reven = entry.getValue();
				if (allMap.floorKey(cost) == null || allMap.get(allMap.floorKey(cost)) < reven) {
					allMap.put(cost, reven);
				}
			}
		}
		return new int[] { allMap.floorKey(allTime), allMap.get(allMap.floorKey(allTime)) };
	}

	public static void main(String[] args) {
		int allTime = 10;
		int[] revenue = { 2000, 4000, 2500, 1600, 3800, 2600, 4000, 3500 };
		int[] times = { 3, 3, 2, 1, 4, 2, 4, 3 };
		int[][] dependents = { 
				{ 0, 1, 1, 0, 0, 0, 0, 0 }, 
				{ 0, 0, 0, 1, 1, 0, 0, 0 }, 
				{ 0, 0, 0, 1, 0, 0, 0, 0 },
				{ 0, 0, 0, 0, 1, 1, 1, 0 }, 
				{ 0, 0, 0, 0, 0, 0, 0, 1 }, 
				{ 0, 0, 0, 0, 0, 0, 0, 1 },
				{ 0, 0, 0, 0, 0, 0, 0, 1 },
				{ 0, 0, 0, 0, 0, 0, 0, 0 } };

		
		int[] res = maxRevenue(allTime, revenue, times, dependents);
		System.out.println(res[0] + " , " + res[1]);
	}

}

逻辑运算符的组合方式

给定一个只由 0(假)、1(真)、&(逻辑与)、|(逻辑或)和^(异或)五种字符组成的字符串express，再给定一个布尔值 desired。返回express能有多少种组合方式，可以达到desired的结果。

【举例】

express="1^0|0|1"，desired=false 只有 1^((0|0)|1)和 1^(0|(0|1))的组合可以得到 false，返回 2。

express="1"，desired=false 无组合则可以得到false，返回0

思路：把字符串用L和R分割，L和R代表小的字符串，因此一定不会踩到逻辑运算符上，所以去搞递归和动态规划。这里的动态规划是搞了一张true表一张false表，注意跳过不需要的点就可以了。

package class08;

public class Problem02_ExpressionNumber {

	public static boolean isValid(char[] exp) {
		if ((exp.length & 1) == 0) {
			return false;
		}
		for (int i = 0; i < exp.length; i = i + 2) {
			if ((exp[i] != '1') && (exp[i] != '0')) {
				return false;
			}
		}
		for (int i = 1; i < exp.length; i = i + 2) {
			if ((exp[i] != '&') && (exp[i] != '|') && (exp[i] != '^')) {
				return false;
			}
		}
		return true;
	}

	public static int num1(String express, boolean desired) {
		if (express == null || express.equals("")) {
			return 0;
		}
		char[] exp = express.toCharArray();
		//0 2 4 6位置上的值不是0就是1，因为这种逻辑运算符是两两结合 
		if (!isValid(exp)) {
			return 0;
		}
		return p(exp, desired, 0, exp.length - 1);
	}

	// exp[L..R] 返回期待为desired的组合方法数
	// 潜台词：L R 一定不要压中逻辑符号
	public static int p(char[] exp, boolean desired, int L, int R) {
		if (L == R) {// base case 1
			if (exp[L] == '1') { 
				return desired ? 1 : 0;
			} else {// '0'
				return desired ? 0 : 1;
			}
		}
		
		//L..R  不止一个字符， 3 5 7 9 
		int res = 0;
		if (desired) { //期待为true
			// i位置尝试L..R范围上的每一个逻辑符号，都是最后结合的
			for (int i = L + 1; i < R; i += 2) {
				switch (exp[i]) {
				case '&':
					res += p(exp, true, L, i - 1) * p(exp, true, i + 1, R);
					break;
				case '|':
					res += p(exp, true, L, i - 1) * p(exp, false, i + 1, R);
					res += p(exp, false, L, i - 1) * p(exp, true, i + 1, R);
					res += p(exp, true, L, i - 1) * p(exp, true, i + 1, R);
					break;
				case '^':
					res += p(exp, true, L, i - 1) * p(exp, false, i + 1, R);
					res += p(exp, false, L, i - 1) * p(exp, true, i + 1, R);
					break;
				}
			}
		} else {
			for (int i = L + 1; i < R; i += 2) {
				switch (exp[i]) {
				case '&':
					res += p(exp, false, L, i - 1) * p(exp, true, i + 1, R);
					res += p(exp, true, L, i - 1) * p(exp, false, i + 1, R);
					res += p(exp, false, L, i - 1) * p(exp, false, i + 1, R);
					break;
				case '|':
					res += p(exp, false, L, i - 1) * p(exp, false, i + 1, R);
					break;
				case '^':
					res += p(exp, true, L, i - 1) * p(exp, true, i + 1, R);
					res += p(exp, false, L, i - 1) * p(exp, false, i + 1, R);
					break;
				}
			}
		}
		return res;
	}

	public static int num2(String express, boolean desired) {
		if (express == null || express.equals("")) {
			return 0;
		}
		char[] exp = express.toCharArray();
		if (!isValid(exp)) {
			return 0;
		}
		int[][] t = new int[exp.length][exp.length];
		int[][] f = new int[exp.length][exp.length];
		t[0][0] = exp[0] == '0' ? 0 : 1;
		f[0][0] = exp[0] == '1' ? 0 : 1;
		for (int i = 2; i < exp.length; i += 2) {
			t[i][i] = exp[i] == '0' ? 0 : 1;
			f[i][i] = exp[i] == '1' ? 0 : 1;
			for (int j = i - 2; j >= 0; j -= 2) {
				for (int k = j; k < i; k += 2) {
					if (exp[k + 1] == '&') {
						t[j][i] += t[j][k] * t[k + 2][i];
						f[j][i] += (f[j][k] + t[j][k]) * f[k + 2][i] + f[j][k] * t[k + 2][i];
					} else if (exp[k + 1] == '|') {
						t[j][i] += (f[j][k] + t[j][k]) * t[k + 2][i] + t[j][k] * f[k + 2][i];
						f[j][i] += f[j][k] * f[k + 2][i];
					} else {
						t[j][i] += f[j][k] * t[k + 2][i] + t[j][k] * f[k + 2][i];
						f[j][i] += f[j][k] * f[k + 2][i] + t[j][k] * t[k + 2][i];
					}
				}
			}
		}
		return desired ? t[0][t.length - 1] : f[0][f.length - 1];
	}

	public static void main(String[] args) {
		String express = "1^0&0|1&1^0&0^1|0|1&1";
		boolean desired = true;
		System.out.println(num1(express, desired));
		System.out.println(num2(express, desired));

	}

}

最长没有重复字符子串的长度

在一个字符串中找到没有重复字符子串中最长的长度。

例如：

abcabcbb没有重复字符的最长子串是abc，长度为3

bbbbb，答案是b，长度为1

pwwkew，答案是wke，长度是3

要求：答案必须是子串，"pwke" 是一个子字符序列但不是一个子字符串。

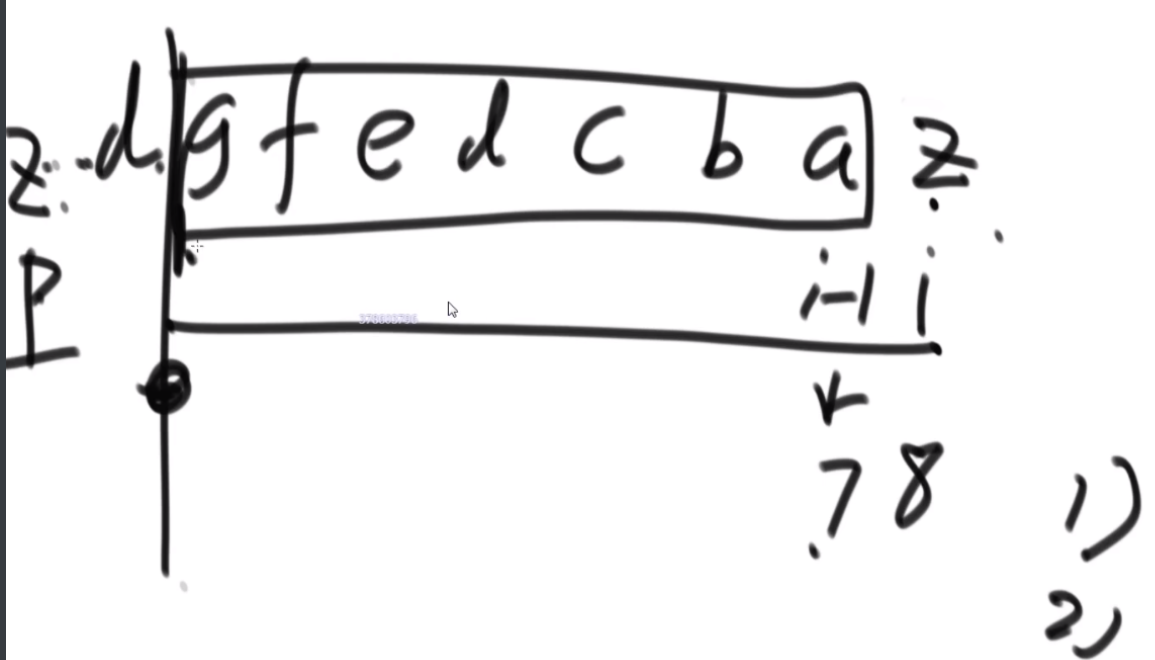
思路：有点类似于KMP，搞一个数组去记录，z位置长度有两种情况，第一种是i-1位置往前推7个长度里有z，那么z位置的值就小于7，另一种是z在很前的地方，那么就是7+1=8.总之有两种瓶颈，选择最短的那个。

package class08;

public class Problem04_LongestNoRepeatSubstring {

	public static int maxUnique(String str) {
		if (str == null || str.equals("")) {
			return 0;
		}
		char[] chas = str.toCharArray();
		// map代替了哈希表 假设字符的码是0~255
		int[] map = new int[256];
		for (int i = 0; i < 256; i++) {
			map[i] = -1;
		}
		int len = 0;
		int pre = -1;
		int cur = 0;
		for (int i = 0; i != chas.length; i++) {
			//瓶颈1 pre：i-1位置的长度是什么 map[chas[i]]上次这个字符出现在哪
			//位置的最大值：即离我最近的那个，所以是长度最短
			pre = Math.max(pre, map[chas[i]]);
			cur = i - pre;//推到的距离确定为i-pre
			len = Math.max(len, cur);//比较保留最长的那个
			map[chas[i]] = i;//更新i位置字符 留给下一次这个字符出现的时候使用
		}
		return len;
	}

	// for test
	public static String getRandomString(int len) {
		char[] str = new char[len];
		int base = 'a';
		int range = 'z' - 'a' + 1;
		for (int i = 0; i != len; i++) {
			str[i] = (char) ((int) (Math.random() * range) + base);
		}
		return String.valueOf(str);
	}

	// for test
	public static String maxUniqueString(String str) {
		if (str == null || str.equals("")) {
			return str;
		}
		char[] chas = str.toCharArray();
		int[] map = new int[256];
		for (int i = 0; i < 256; i++) {
			map[i] = -1;
		}
		int len = -1;
		int pre = -1;
		int cur = 0;
		int end = -1;
		for (int i = 0; i != chas.length; i++) {
			pre = Math.max(pre, map[chas[i]]);
			cur = i - pre;
			if (cur > len) {
				len = cur;
				end = i;
			}
			map[chas[i]] = i;
		}
		return str.substring(end - len + 1, end + 1);
	}

	public static void main(String[] args) {
		String str = getRandomString(20);
		System.out.println(str);
		System.out.println(maxUnique(str));
		System.out.println(maxUniqueString(str));
	}
}

str1编辑成str2的最小代价

给定两个字符串str1和str2，再给定三个整数ic、dc和rc，分别代表插入、删除和替换一个字符的代价，返回将str1编辑成str2的最小代价。

【举例】

str1="abc"，str2="adc"，ic=5，dc=3，rc=2 从"abc"编辑成"adc"，把'b'替换成'd'是代价最小的，所以返回2

str1="abc"，str2="adc"，ic=5，dc=3，rc=100 从"abc"编辑成"adc"，先删除'b'，然后插入'd'是代价最小的，所以返回8

str1="abc"，str2="abc"，ic=5，dc=3，rc=2 不用编辑了，本来就是一样的字符串，所以返回0

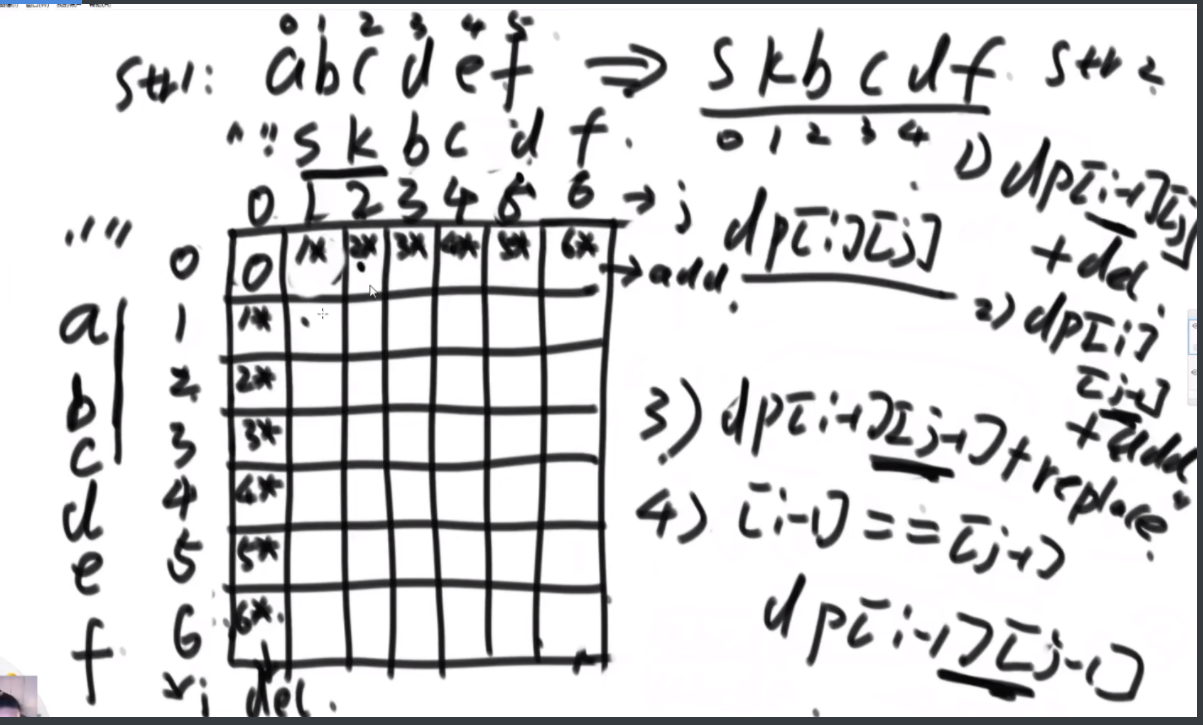
思路：这个表格代表的是从空串开始到达列的串的代价，第二行第三列就是a变成sk的代价，先把第一行和第一列算出来，然后推下面。

str1变成str2分成4种情况，第一种：假设str1:abcde str2:abcd 那么str1可以先前四个让它一样，然后删掉最后一个，第二种：假设str1:abcd str2:abcde 那么str1可以先前四个让它一样，然后加上最后一个，第三种：假设str1:abcds str2:abcde 那么str1可以先前四个让它一样，然后替换掉最后一个，第四种：假设str1:abcfe str2:abcde 那么str1可以先前四个让它一样，然后最后一个什么也不需要做。那么每个位置的代价，仅与它左侧上侧以及左上角的位置的代价有关系。

这个题通过信息检索技术的作业再加上和飞哥的讨论有的新的理解：

每个位置上的值分为了四个部分，假设第二行第三列（2，3），S和O，意义是OS变成SNO的代价。可以有3中来源，

1. 如果S==O，那么左上角的值为（1，2）否则为（1，2）+替换的代价，原理是O先变成SN，然后看S和O是否相等，如果相等，直接为O变成SN的代价，否则还得加上一个替换的代价。因此这个位置的左上角的数为2+1=3
2. 左下角的值为(2,2)+1,即2+insert的代价，原理是OS先变为SN，然后插入一个O。
3. 右上角的值为（1，3）+delete的代价，原理是先把S删掉，然后O到SNO的代价。
4. 这三个值中的最小值为当前位置的结果，即最小代价。

这个题通过自己的思考有了更深入的了解，还不错。

package class08;

public class Problem05_EditCost {

	public static int minCost1(String str1, String str2, int ic, int dc, int rc) {
		if (str1 == null || str2 == null) {
			return 0;
		}
		char[] chs1 = str1.toCharArray();
		char[] chs2 = str2.toCharArray();
		int row = chs1.length + 1;
		int col = chs2.length + 1;
		int[][] dp = new int[row][col];
		for (int i = 1; i < row; i++) {
			dp[i][0] = dc * i;
		}
		for (int j = 1; j < col; j++) {
			dp[0][j] = ic * j;
		}
		for (int i = 1; i < row; i++) {
			for (int j = 1; j < col; j++) {
				if (chs1[i - 1] == chs2[j - 1]) { //情况4
					dp[i][j] = dp[i - 1][j - 1];
				} else {
					dp[i][j] = dp[i - 1][j - 1] + rc;//情况3
				}
				dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + ic); //情况2
				dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + dc); //情况1
			}
		}
		return dp[row - 1][col - 1];
	}

	public static int minCost2(String str1, String str2, int ic, int dc, int rc) {
		if (str1 == null || str2 == null) {
			return 0;
		}
		char[] chs1 = str1.toCharArray();
		char[] chs2 = str2.toCharArray();
		char[] longs = chs1.length >= chs2.length ? chs1 : chs2;
		char[] shorts = chs1.length < chs2.length ? chs1 : chs2;
		if (chs1.length < chs2.length) { // str2�ϳ��ͽ���ic��dc��ֵ
			int tmp = ic;
			ic = dc;
			dc = tmp;
		}
		int[] dp = new int[shorts.length + 1];
		for (int i = 1; i <= shorts.length; i++) {
			dp[i] = ic * i;
		}
		for (int i = 1; i <= longs.length; i++) {
			int pre = dp[0]; // pre��ʾ���Ͻǵ�ֵ
			dp[0] = dc * i;
			for (int j = 1; j <= shorts.length; j++) {
				int tmp = dp[j]; // dp[j]û����ǰ�ȱ�������
				if (longs[i - 1] == shorts[j - 1]) {
					dp[j] = pre;
				} else {
					dp[j] = pre + rc;
				}
				dp[j] = Math.min(dp[j], dp[j - 1] + ic);
				dp[j] = Math.min(dp[j], tmp + dc);
				pre = tmp; // pre���dp[j]û����ǰ��ֵ
			}
		}
		return dp[shorts.length];
	}

	public static void main(String[] args) {
		String str1 = "ab12cd3";
		String str2 = "abcdf";
		System.out.println(minCost1(str1, str2, 5, 3, 2));
		System.out.println(minCost2(str1, str2, 5, 3, 2));

		str1 = "abcdf";
		str2 = "ab12cd3";
		System.out.println(minCost1(str1, str2, 3, 2, 4));
		System.out.println(minCost2(str1, str2, 3, 2, 4));

		str1 = "";
		str2 = "ab12cd3";
		System.out.println(minCost1(str1, str2, 1, 7, 5));
		System.out.println(minCost2(str1, str2, 1, 7, 5));

		str1 = "abcdf";
		str2 = "";
		System.out.println(minCost1(str1, str2, 2, 9, 8));
		System.out.println(minCost2(str1, str2, 2, 9, 8));

	}

}

**使字符串的字典序最小 **

给定一个全是小写字母的字符串str，删除多余字符，使得每种字符只保留一个，并让最终结果字符串的字典序最小

【举例】

str = "acbc"，删掉第一个'c'，得到"abc"，是所有结果字符串中字典序最小的。

str = "dbcacbca"，删掉第一个'b'、第一个'c'、第二个'c'、第二个'a'，得到"dabc"， 是所有结果字符串中字典序最小的。

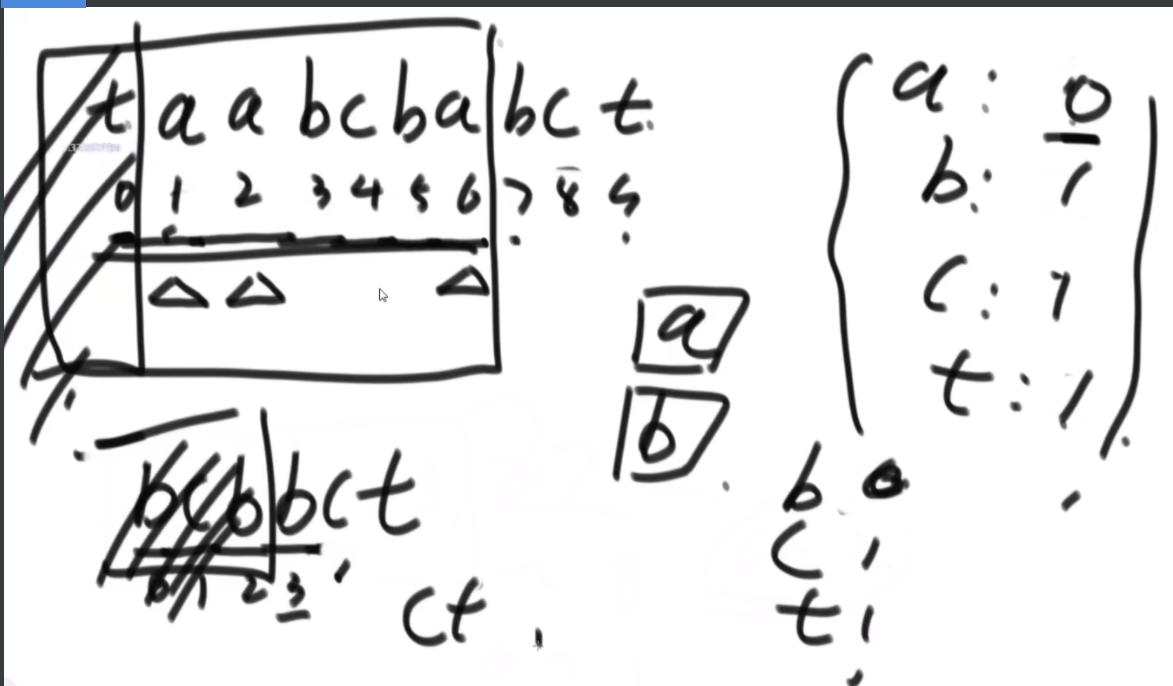
思路：首先，遍历一遍记住这些字符的出现次数，然后从头开始搞，每过一个就对应字符-1，直到有的字符已经减没了快，那么左边的里面挑一个阿斯克码最小的就完事了。

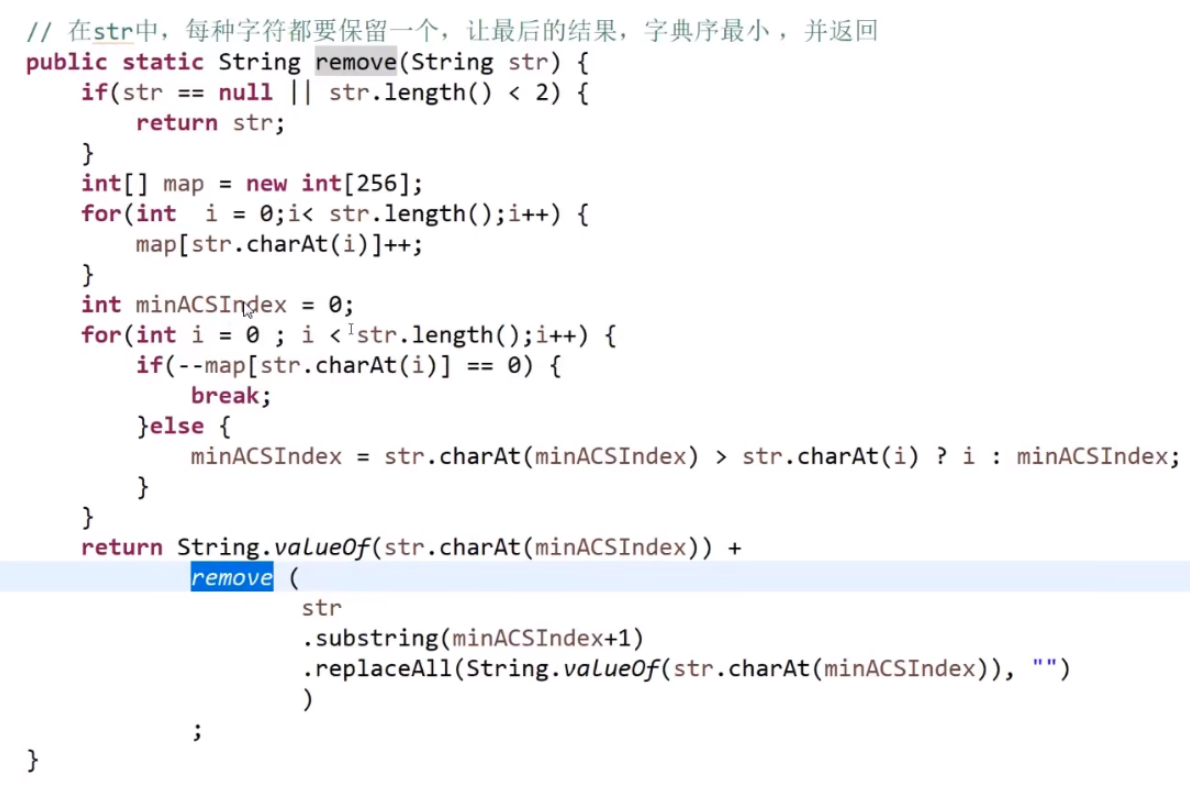
minACSIndex字符是记录阿斯克码最小的那个，然后把其他字符替换为空，接上后面，完事。

时间复杂度O(K*N) K种字符

输入字符串输出字典中编码

在数据加密和数据压缩中常需要对特殊的字符串进行编码。给定的字母表A由26个小写英文字母组成，即

A={a, b...z}。该字母表产生的长序字符串是指定字符串中字母从左到右出现的次序与字母在字母表中出现

的次序相同，且每个字符最多出现1次。例如，a，b，ab，bc，xyz等字符串是升序字符串。对字母表A产生

的所有长度不超过6的升序字符串按照字典排列编码如下：a(1)，b(2)，c(3)……，z(26)，ab(27)，

ac(28)……对于任意长度不超过16的升序字符串，迅速计算出它在上述字典中的编码。

输入描述： 第1行是一个正整数N，表示接下来共有N行，在接下来的N行中，每行给出一个字符串。

输出描述： 输出N行，每行对应于一个字符串编码。

示例1:

输入

3

a

b

ab

输出

1

2

27

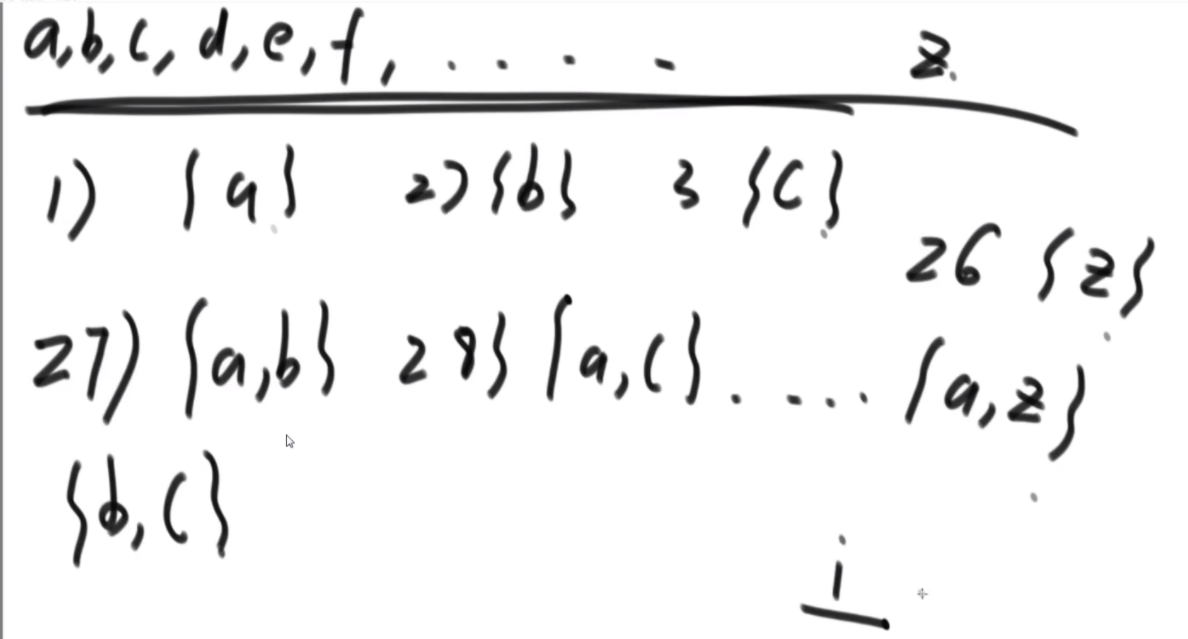
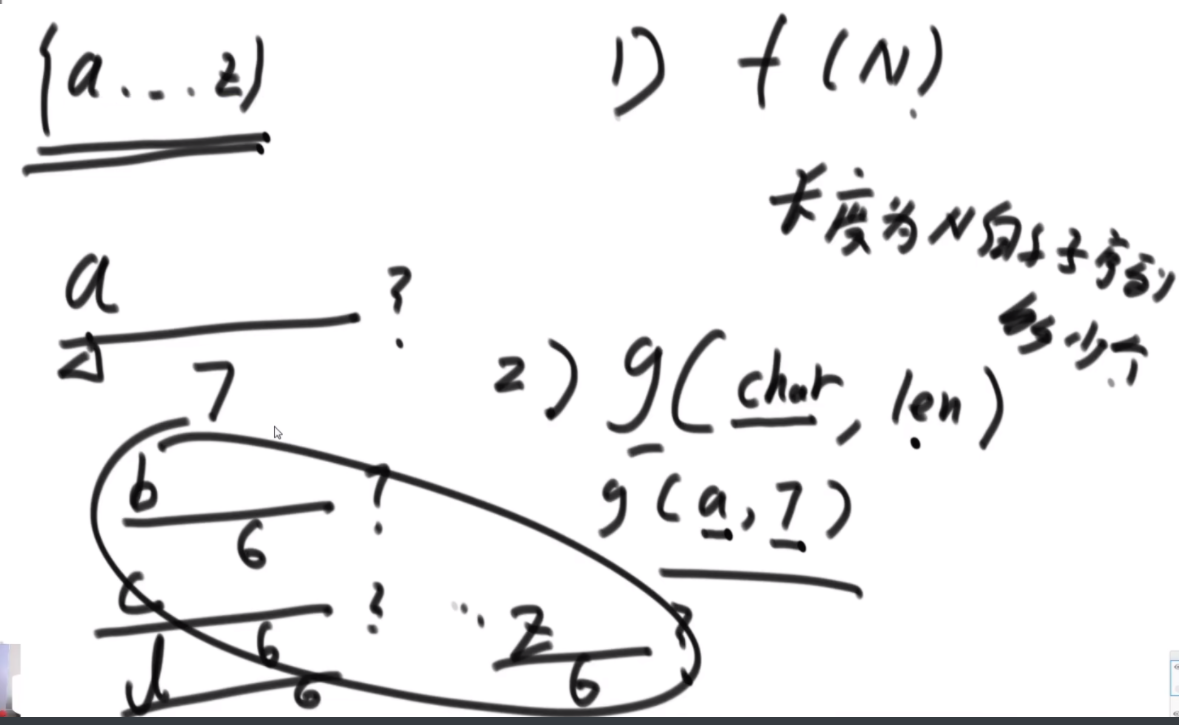
思路：搞一个f(N)函数，用来计算长度为N的子序列有多少个，一个g（char,len）函数，计算以char字符开头的长度为len的子序列有多少个，先去看g咋弄，假设是a，长度为7，那么应该为g(ab,6)+g(ac,6)+g(ad,6)..+g(az,6)，然后g(ab,6)又可以拆分为g(abc,5)+g(abd,5)..+g(abz,5)，依次递归。

代码中f和g是反的。

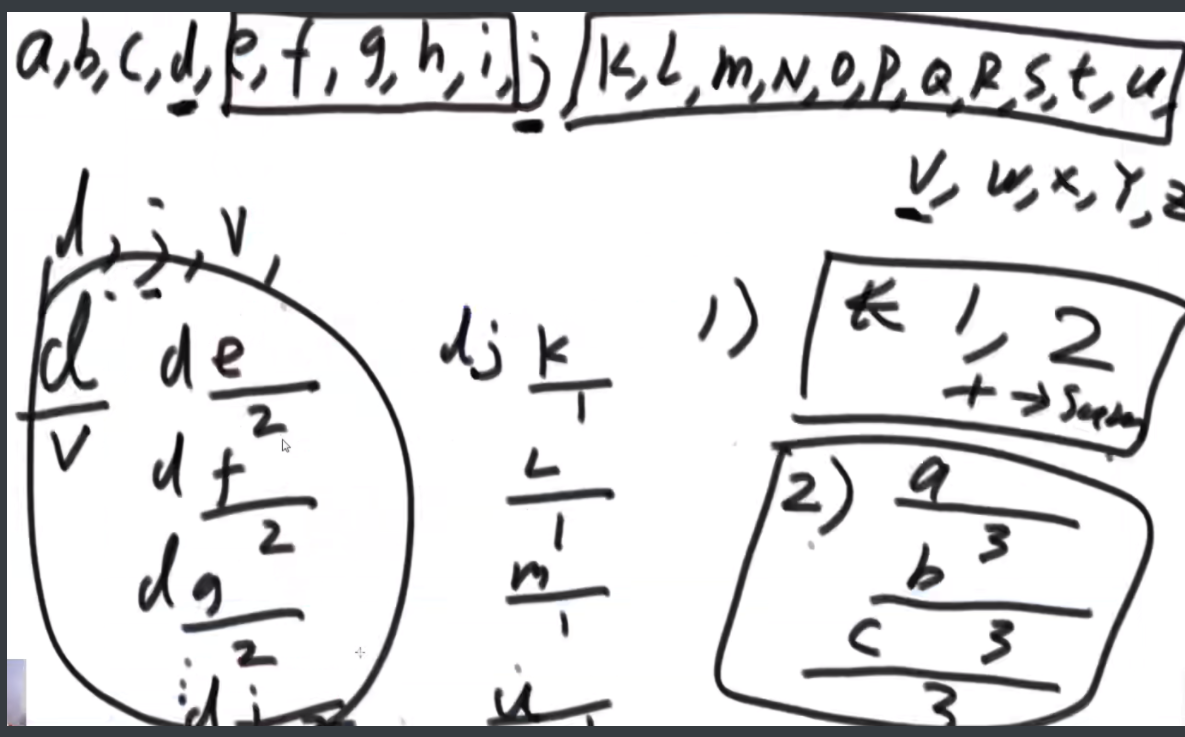
举例：假设求"djv"的编码，那么需要分成4部分：

1. 长度为1、2的所有序列
2. 长度为3的d之前的所有开头，(a,3)..(c,3)
3. 这样d就定下来了，接下来是de,2，即（e,2）。。。一直到j之前
4. 然后是j订下来，a-v之前。

p26:

最少的点亮灯的数量

小Q正在给一条长度为n的道路设计路灯安置方案。为了让问题更简单,小Q把道路视为n个方格,需要照亮的地方用'.'表示, 不需要照亮的障碍物格子用'X'表示。小Q现在要在道路上设置一些路灯, 对于安置在pos位置的路灯, 这盏路灯可以照亮pos - 1, pos, pos + 1这三个位置。小Q希望能安置尽量少的路灯照亮所有'.'区域, 希望你能帮他计算一下最少需要多少盏路灯。

输入描述： 输入的第一行包含一个正整数t(1 <= t <= 1000), 表示测试用例数接下来每两行一个测试数据, 第一行一个正整数n(1 <= n <= 1000),表示道路的长度。第二行一个字符串s表示道路的构造,只包含'.'和'X'。

输出描述： 对于每个测试用例, 输出一个正整数表示最少需要多少盏路灯。

思路：当前index位置是x则index+1，是.则路灯+1，下一个如果是x则index+2，下一个如果是.则index+3，直接假设路灯放在了中间位置，不管中间是啥都能照亮了。

package ZuoShen2.ZhongClass02;

public class Light {
    //至少需要多少等，可以把.都点亮
    public static int minLight(String s){
        char[] str = s.toCharArray();
        int index = 0;
        int light = 0;
        //当你来到i位置，一定要保证之前的灯，彻底不会影响到i位置
        while(index< str.length){
            if(str[index] == 'X'){
                index++;
            }else { // str[index] == '.'
                light++;
                if(str[index+1] == 'X'){
                    index = index+2;
                }else { //下一个位置是'.'
                    index = index+3;
                }
            }
        }
        return light;
    }
}

中序和先序转后序遍历

已知一棵二叉树中没有重复节点，并且给定了这棵树的中序遍历数组和先序遍历数组，返回后序遍历数组。

比如给定： int[] pre = { 1, 2, 4, 5, 3, 6, 7 }; int[] in = { 4, 2, 5, 1, 6, 3, 7 };

返回： {4,5,2,6,7,3,1}

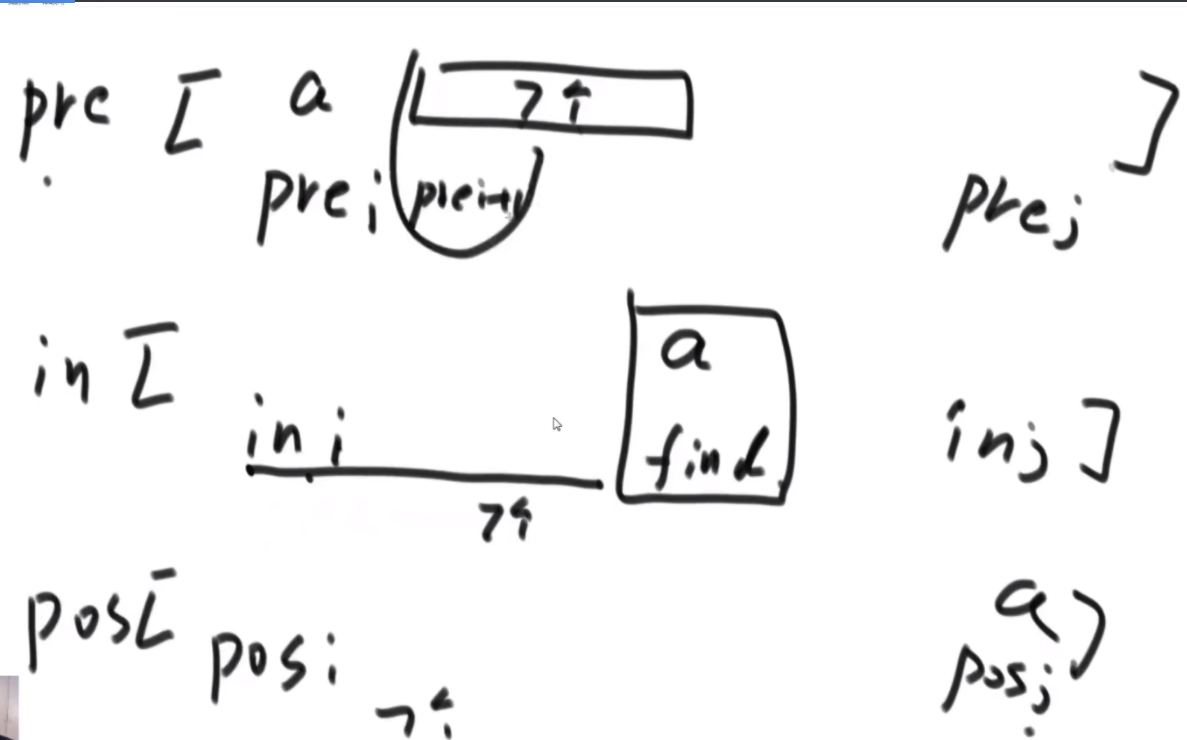
思路：先找到头结点，然后把头结点放在最后，然后在中序里面遍历去找到头结点a，然后分成两截继续去递归遍历。

优化：这里在中序中寻找头结点的过程可以优化。

package class06;

import java.util.HashMap;

public class Problem04_PreAndInArrayToPosArray {

	public static int[] getPosArray(int[] pre, int[] in) {
		if (pre == null || in == null) {
			return null;
		}
		int len = pre.length;
		int[] pos = new int[len];
		HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
		for (int i = 0; i < len; i++) {
			map.put(in[i], i);
		}
		setPos(pre, 0, len - 1, in, 0, len - 1, pos, len - 1, map);
		return pos;
	}

	public static int setPos(int[] p, int pi, int pj, int[] n, int ni, int nj, int[] s, int si,
			HashMap<Integer, Integer> map) {
		if (pi > pj) {
			return si;
		}
		s[si--] = p[pi];
		int i = map.get(p[pi]);
		si = setPos(p, pj - nj + i + 1, pj, n, i + 1, nj, s, si, map);
		return setPos(p, pi + 1, pi + i - ni, n, ni, i - 1, s, si, map);
	}

	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int[] pre = { 1, 2, 4, 5, 3, 6, 7 };
		int[] in = { 4, 2, 5, 1, 6, 3, 7 };
		int[] pos = getPosArray(pre, in);
		printArray(pos);

	}
}

完全二叉树节点的个数

求完全二叉树节点的个数

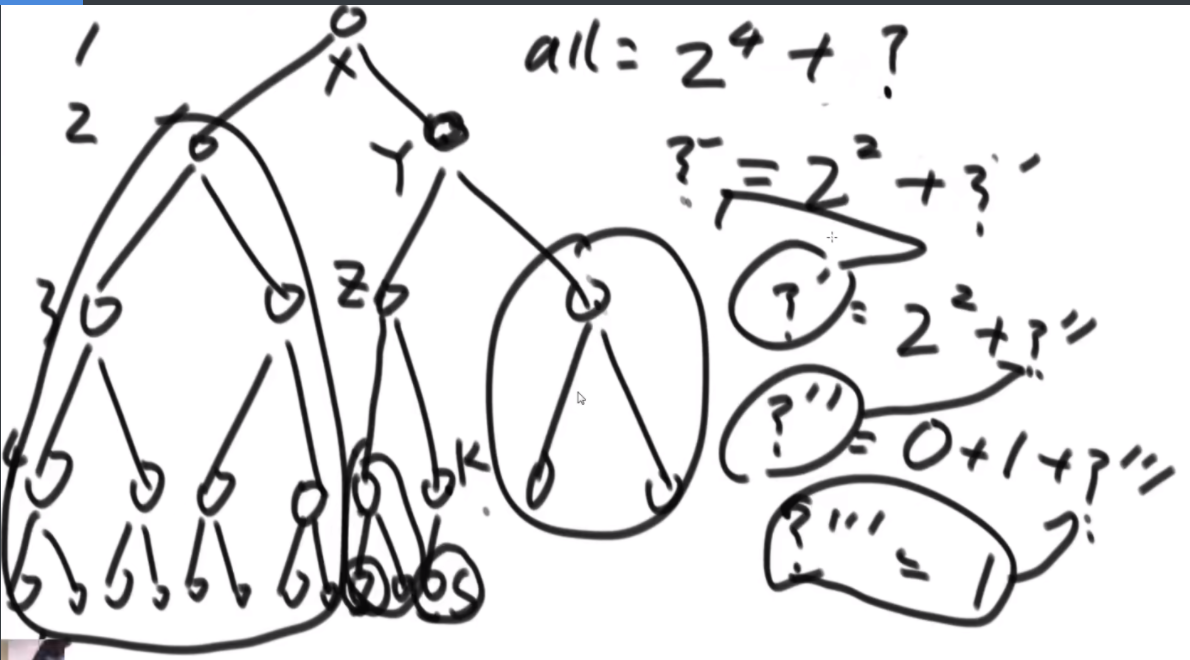
思路：看右子树的最左节点是否到达最下面那层，如果到了，说明左子树是满的，直接通过高度求出来，如果没到，那在倒数第二层，现在去求右子树Y的节点数。然后看右子树的最左节点，发现没到最下面一层，那么说明右子树是满的，去求左子树Z，然后看Z的右子树的最左节点在最下面一层，说明Z的左子树是满的，求右子树K的节点数，然后以此类推，直到树为空。

时间复杂度分析：O(h²)即O((logN)²)，之前是O(n)

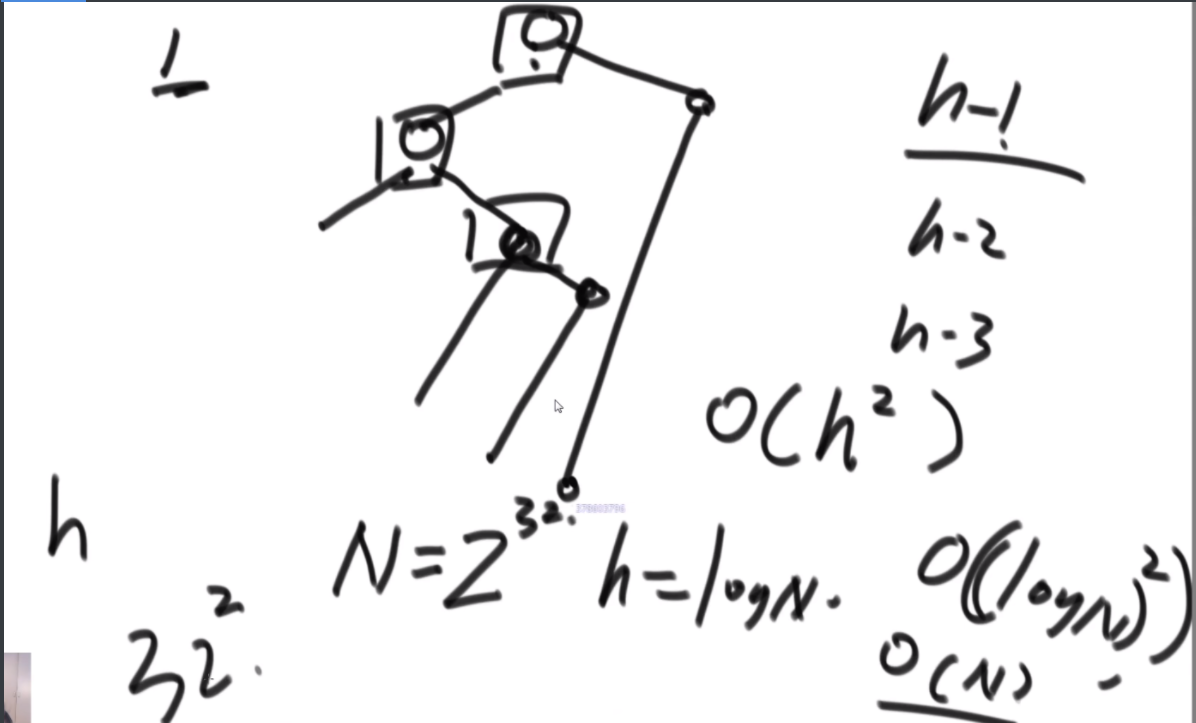
package class07;

public class Problem05_CompleteTreeNodeNumber {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static int nodeNum(Node head) {
		if (head == null) {
			return 0;
		}
		return bs(head, 1, mostLeftLevel(head, 1));
	}
	
    //node在第level层，h是总的深度(h永远不变，全局变量)
    //以node为头的完全二叉树，节点个数是多少
	public static int bs(Node node, int l, int h) {
		if (l == h) {
			return 1;
		}
        //右树的最左节点到了最下面一层
		if (mostLeftLevel(node.right, l + 1) == h) {
            // 2 ^ (h-level)  +  右子树的完全二叉树的节点数
			return (1 << (h - l)) + bs(node.right, l + 1, h);
		} else {//没到最下面一层
            // 2 ^ (h-level-1)  + 左子树的完全二叉树的节点数
			return (1 << (h - l - 1)) + bs(node.left, l + 1, h);
		}
	}

    //先找到level是多少，一直往左走走到空  这个时候层数已经算上叶子节点了，因此要-1
	public static int mostLeftLevel(Node node, int level) {
		while (node != null) {
			level++;
			node = node.left;
		}
		return level - 1;
	}

	public static void main(String[] args) {
		Node head = new Node(1);
		head.left = new Node(2);
		head.right = new Node(3);
		head.left.left = new Node(4);
		head.left.right = new Node(5);
		head.right.left = new Node(6);
		System.out.println(nodeNum(head));

	}

}

最长递增子序列问题

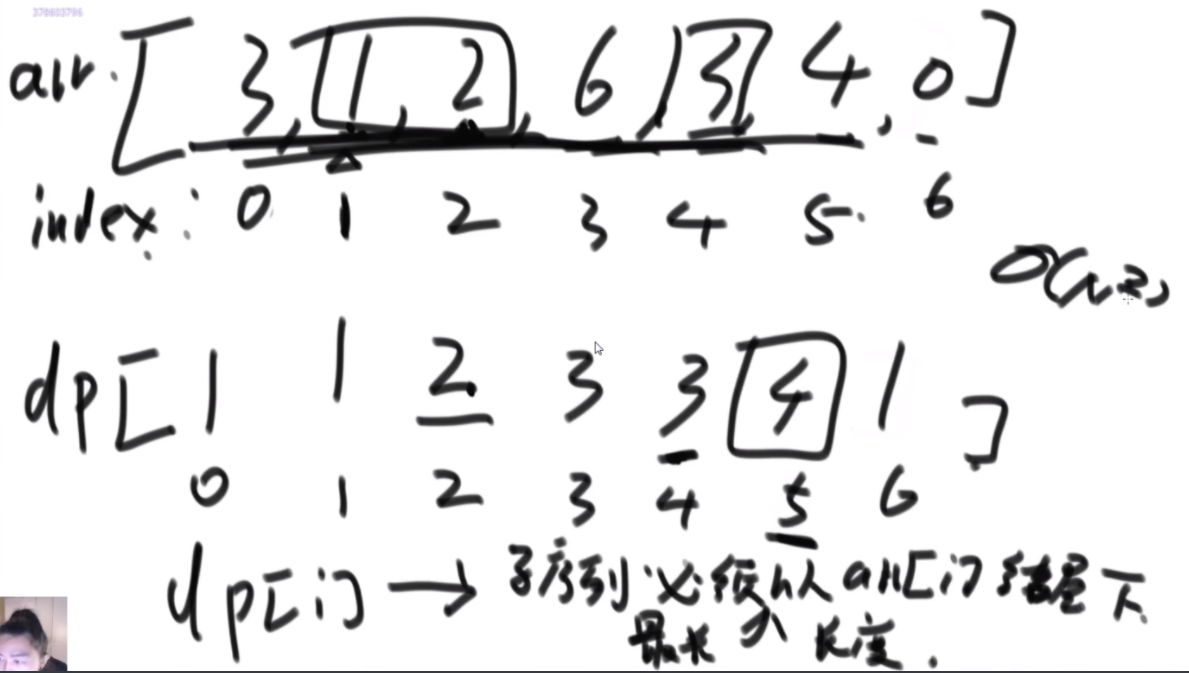
普通思路：搞一个数组，记录再i位置上，必须以arr[i]结尾的最长子序列的长度。然后，每个长度从头开始找比自己小的，把该位置上的值加起来，最后找到最大的，完事。O(N²)

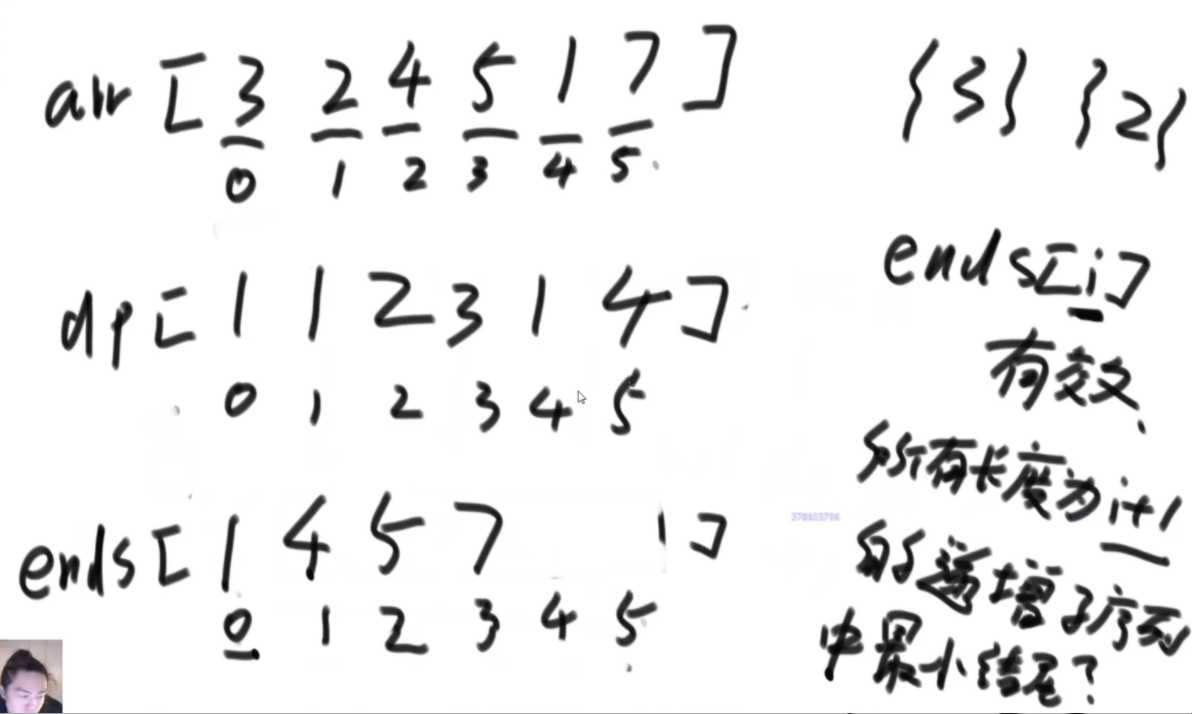
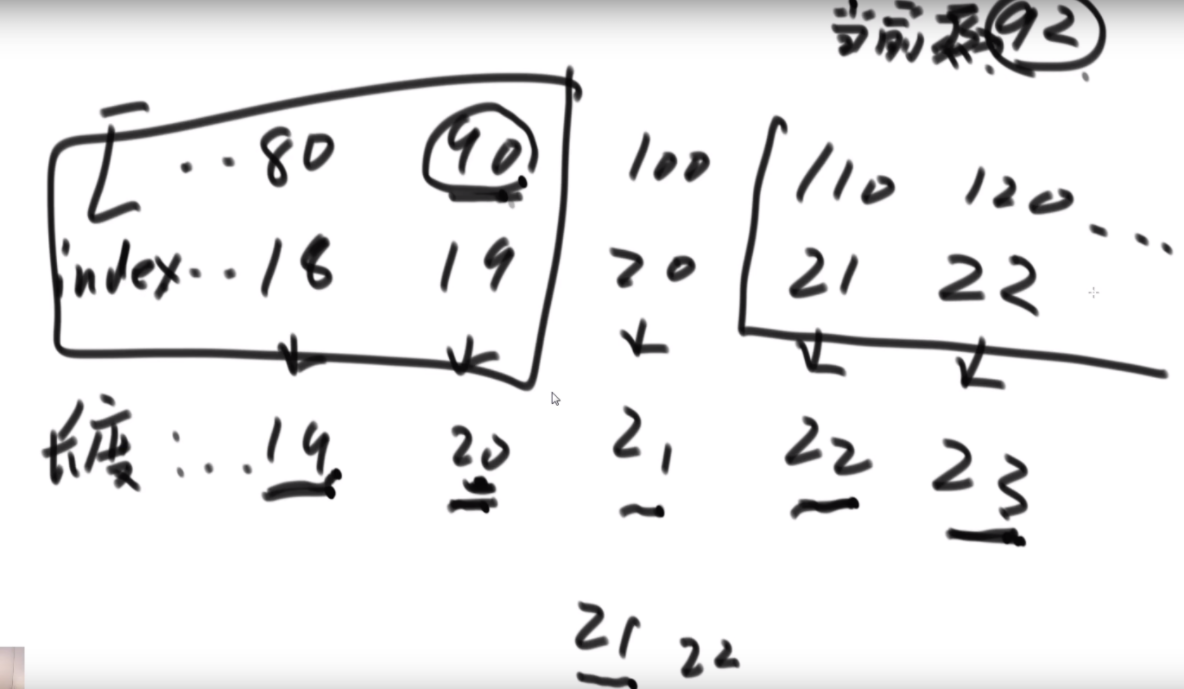
优化思路：搞一个ends数组，记录有效区，一开始全是无效区。end[i]的含义：所有长度为i+1的递增子序列中，最小结尾是什么值（根据题意，必有序）。每过一个值先看ends的有校区中比它大的最左的位置，去更新，然后看这个值连同自己往左数一共有多少个数就是多少个dp值；如果没找到比它大的，那么扩充有效区，更新dp。

第二张图解释了第一个情况，因为ends中记录的是长度为i+1的递增子序列的最小结尾，因为92>90因此没法更新比它小的数，看后面，假如更新了110的话，那么100和92就冲突了，那么这个数列就不是递增的不符合题意。因此92去更新100.

原理：将第一种思路的动态规划中的向左侧的枚举行为用数组替代，构建单调性！！

快速判断能否被3整除

小Q得到一个神奇的数列: 1, 12, 123,...12345678910,1234567891011...。并且小Q对于能否被3整除这个性质很感兴趣。 小Q现在希望你能帮他计算一下从数列的第l个到第r个(包含端点)有多少个数可以被3整除。

输入描述：

输入包括两个整数l和r(1 <= l <= r <= 1e9), 表示要求解的区间两端。

输出描述：

输出一个整数, 表示区间内能被3整除的数字个数。

示例1:

输入

2 5

输出

3

解题思路：判断一个数能不能被3整除，等价于一个数的每位之和能否被3整除。刚开始想打表，但发现数据量是1e9，一维数组最多只能开到1e8.所以就纯暴力判断了，不过数据是有规律的，第一个数是1、第二个数是12，第三个数是123，所以只用判断n*(n+1)/2%3即可。因为数量太大了，所以用long long

思路：给100，那么搞一个等差数列1+2+3+..+100看能否%3，完事。

p25:

画出路径的目录结构

给你一个字符串类型的数组arr，譬如：

String[] arr = { "b\cst", "d\", "a\d\e", "a\b\c" };

你把这些路径中蕴含的目录结构给画出来，子目录直接列在父目录下面，并比父目录

向右进两格，就像这样:

a

​ b

​ c

​ d

​ e

b

​ cst

d

同一级的需要按字母顺序排列，不能乱。

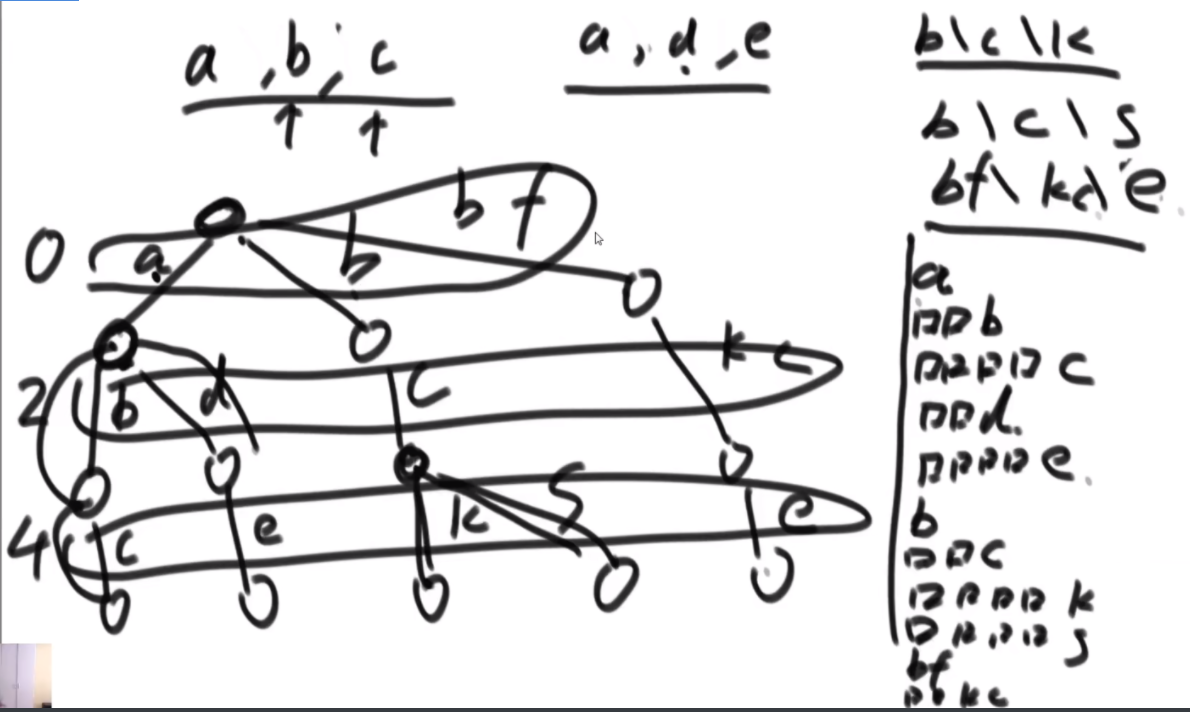
思路：搞一个前缀树，然后进行深度优先遍历，第一层0个空格，第二层的两个空格，第三层的三个空格，以此类推。。重点是如何生成前缀树见p9。

package class06;

import java.util.TreeMap;

public class Problem01_GetFolderTree {

	public static class Node {
		public String name;
		public TreeMap<String, Node> nextMap;

		public Node(String name) {
			this.name = name;
			nextMap = new TreeMap<>();
		}
	}

	public static void print(String[] folderPaths) {
		if (folderPaths == null || folderPaths.length == 0) {
			return;
		}
		Node head = generateFolderTree(folderPaths);
		printProcess(head, 0);
	}

	public static Node generateFolderTree(String[] folderPaths) {
		Node head = new Node("");
		for (String foldPath : folderPaths) {
            //split是正则匹配 \\代表按照\分割，然后\\\\代表\\因此没问题
			String[] paths = foldPath.split("\\\\");
			Node cur = head;
			for (int i = 0; i < paths.length; i++) {
                //如果没有出现过，存入树中
				if (!cur.nextMap.containsKey(paths[i])) {
					cur.nextMap.put(paths[i], new Node(paths[i]));
				}
                //如果出现过||没出现过已经存入了，从树中拿出这个节点给cur   
				cur = cur.nextMap.get(paths[i]);
			}
		}
		return head;
	}

	public static void printProcess(Node head, int level) {
		if (level != 0) {
            //打印空格
			System.out.println(get2nSpace(level) + head.name);
		}
        //深度优先遍历   直接循环头结点的所有nexts，然后对每个的第一个继续调循环
		for (Node next : head.nextMap.values()) {
			printProcess(next, level + 1);
		}
	}

	public static String get2nSpace(int n) {
		String res = "";
		for (int i = 1; i < n; i++) {
			res += "  ";
		}
		return res;
	}

	public static void main(String[] args) {
		String[] arr = { "b\\cst", "d\\", "a\\d\\e", "a\\b\\c" };
		print(arr);
	}

}

搜索二叉树转化成有序双向链表

双向链表节点结构和二叉树节点结构是一样的，如果你把last认为是left，next认为是next的话。

给定一个搜索二叉树的头节点head，请转化成一条有序的双向链表，并返回链表的头节点。

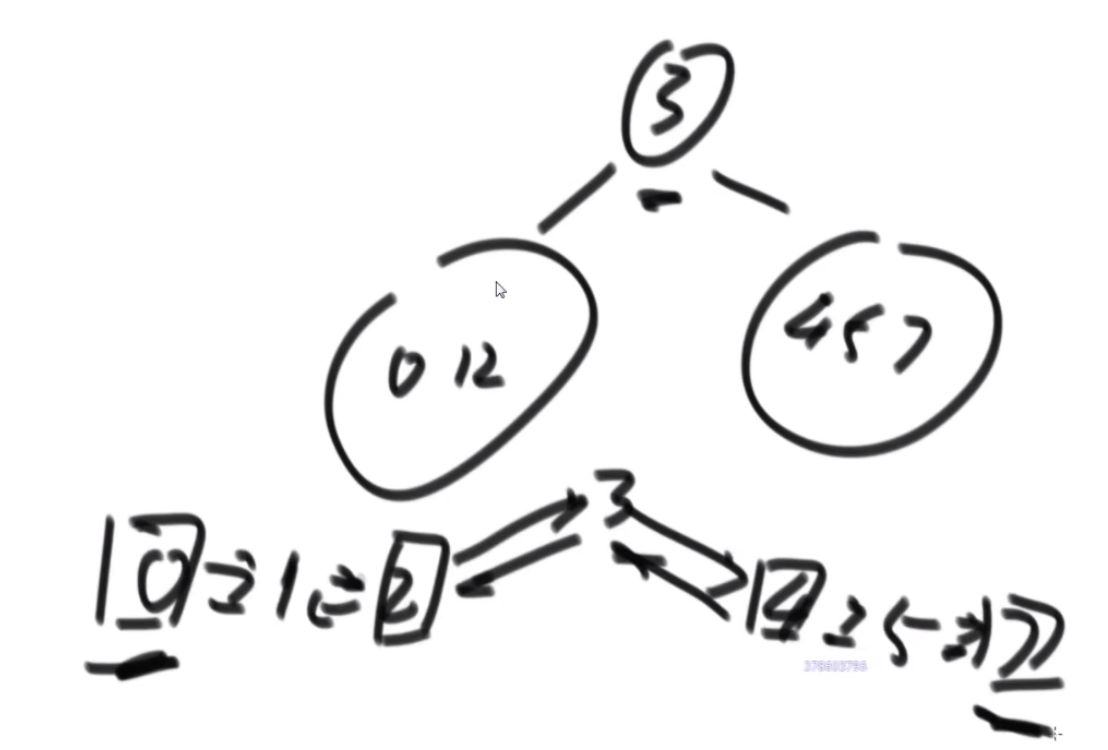
思路:二叉树递归问题的套路，搞一个ReturnType，然后对左右两侧假设弄好了，只弄中间节点即可。

代码主要看convert2

package class06;

import java.util.LinkedList;
import java.util.Queue;

public class Problem02_BSTtoDoubleLinkedList {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static Node convert1(Node head) {
		Queue<Node> queue = new LinkedList<Node>();
		inOrderToQueue(head, queue);
		if (queue.isEmpty()) {
			return head;
		}
		head = queue.poll();
		Node pre = head;
		pre.left = null;
		Node cur = null;
		while (!queue.isEmpty()) {
			cur = queue.poll();
			pre.right = cur;
			cur.left = pre;
			pre = cur;
		}
		pre.right = null;
		return head;
	}

	public static void inOrderToQueue(Node head, Queue<Node> queue) {
		if (head == null) {
			return;
		}
		inOrderToQueue(head.left, queue);
		queue.offer(head);
		inOrderToQueue(head.right, queue);
	}


	public static class RetrunType {
		public Node start;
		public Node end;

		public RetrunType(Node start, Node end) {
			this.start = start;
			this.end = end;
		}
	}
	
	public static Node convert2(Node head) {
		if (head == null) {
			return null;
		}
		return process(head).start;
	}

	//返回整个有序双向链表的头结点和尾节点
	public static RetrunType process(Node head) {
		if (head == null) {
			return new RetrunType(null, null);
		}
		RetrunType leftList = process(head.left);
		RetrunType rightList = process(head.right);
		if (leftList.end != null) {
			//把当前节点练到左侧最右边
			leftList.end.right = head;
		}
		//将head双向指针连上
		head.left = leftList.end;
		head.right = rightList.start;
		if (rightList.start != null) {
			//把当前节点练到右侧最左边
			rightList.start.left = head;
		}
		//判断左右侧为空的情况
		return new RetrunType(leftList.start != null ? leftList.start : head,
				rightList.end != null ? rightList.end : head);
	}

	public static void printBSTInOrder(Node head) {
		System.out.print("BST in-order: ");
		if (head != null) {
			inOrderPrint(head);
		}
		System.out.println();
	}

	public static void inOrderPrint(Node head) {
		if (head == null) {
			return;
		}
		inOrderPrint(head.left);
		System.out.print(head.value + " ");
		inOrderPrint(head.right);
	}

	public static void printDoubleLinkedList(Node head) {
		System.out.print("Double Linked List: ");
		Node end = null;
		while (head != null) {
			System.out.print(head.value + " ");
			end = head;
			head = head.right;
		}
		System.out.print("| ");
		while (end != null) {
			System.out.print(end.value + " ");
			end = end.left;
		}
		System.out.println();
	}

	public static void main(String[] args) {
		Node head = new Node(5);
		head.left = new Node(2);
		head.right = new Node(9);
		head.left.left = new Node(1);
		head.left.right = new Node(3);
		head.left.right.right = new Node(4);
		head.right.left = new Node(7);
		head.right.right = new Node(10);
		head.left.left = new Node(1);
		head.right.left.left = new Node(6);
		head.right.left.right = new Node(8);

		printBSTInOrder(head);
		head = convert1(head);
		printDoubleLinkedList(head);

		head = new Node(5);
		head.left = new Node(2);
		head.right = new Node(9);
		head.left.left = new Node(1);
		head.left.right = new Node(3);
		head.left.right.right = new Node(4);
		head.right.left = new Node(7);
		head.right.right = new Node(10);
		head.left.left = new Node(1);
		head.right.left.left = new Node(6);
		head.right.left.right = new Node(8);

		printBSTInOrder(head);
		head = convert2(head);
		printDoubleLinkedList(head);

	}

}

最大搜索二叉子树的节点个数

找到一棵二叉树中，最大的搜索二叉子树，返回最大搜索二叉子树的节点个数。

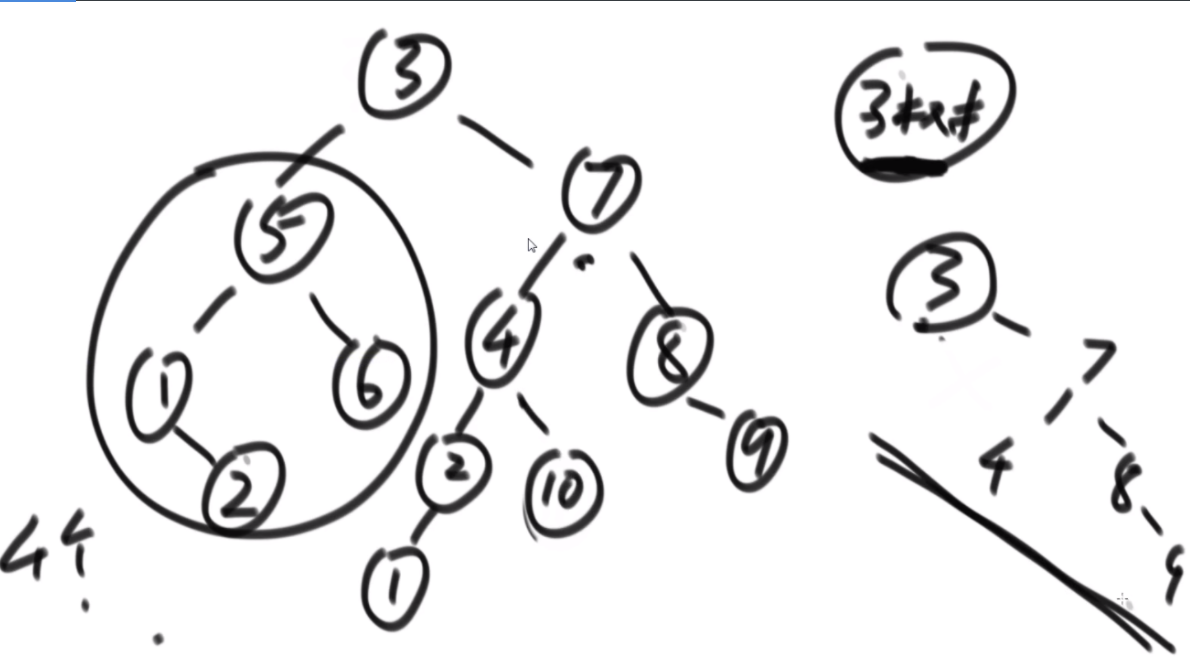
所谓的最大搜索二叉子树是指这个树必须是完整的，如上图中，3的右侧部分不能称之为一个完整的树，因此是5的那一侧。

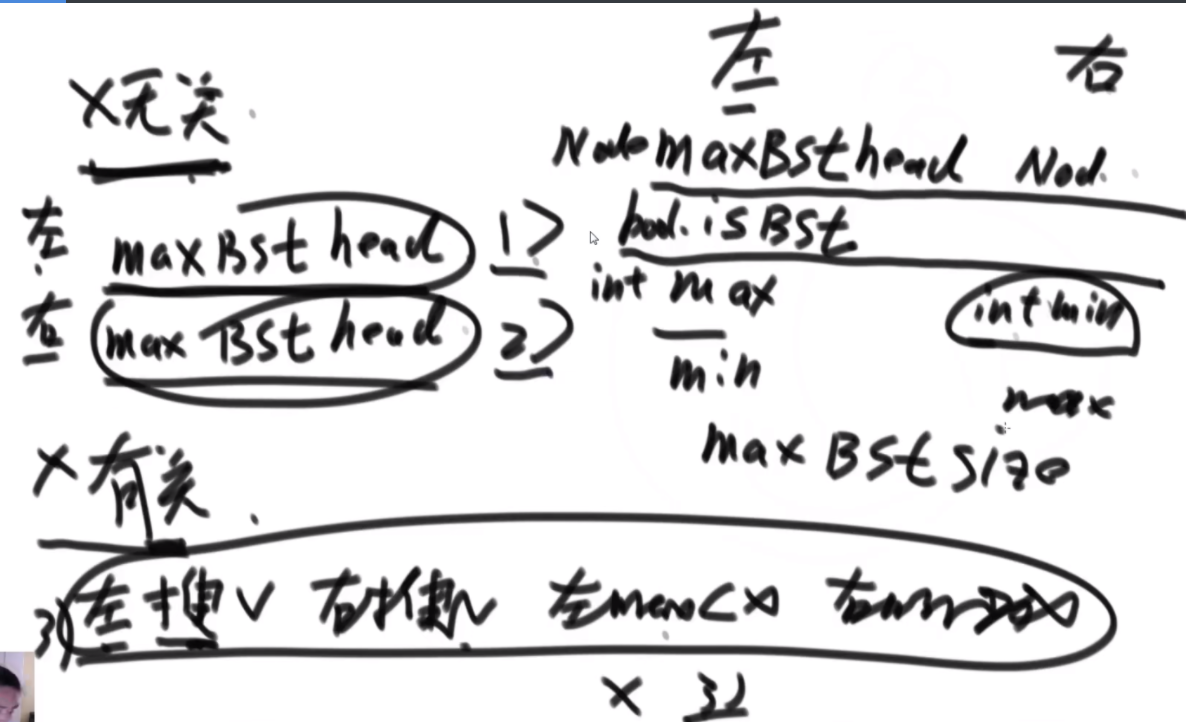
思路：二叉树的递归套路左右返回的必须是一样的，因此虽然左边要的是最大值，右边要的是最小值，还是都要了，而且还要判断是不是搜索二叉树以及最大的子树大小。

1. 可能性一和可能性二是指左树或者右树为答案
2. 可能性三为x是答案

package class06;

public class Problem03_BiggestSubBSTInTree {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static Node getMaxBST(Node head) {
		return process(head).maxBSTHead;
	}

	public static class ReturnType {
		public Node maxBSTHead;
		public int maxBSTSize;
		public int min;
		public int max;

		public ReturnType(Node maxBSTHead, int maxBSTSize, int min, int max) {
			this.maxBSTHead = maxBSTHead;
			this.maxBSTSize = maxBSTSize;
			this.min = min;
			this.max = max;
		}
	}

	public static ReturnType process(Node X) {
		// base case : 如果子树是空树
		// 最小值为系统最大
		// 最大值为系统最小
		if (X == null) {
			return new ReturnType(null, 0, Integer.MAX_VALUE, Integer.MIN_VALUE);
		}
		// 默认直接得到左树全部信息
		ReturnType lData = process(X.left);
		// 默认直接得到右树全部信息
		ReturnType rData = process(X.right);
		// 以下过程为信息整合
		// 同时以X为头的子树也做同样的要求，也需要返回如ReturnType描述的全部信息
		// 以X为头的子树的最小值是：左树最小、右树最小、X的值，三者中最小的
		int min = Math.min(X.value, Math.min(lData.min, rData.min));
		// 以X为头的子树的最大值是：左树最大、右树最大、X的值，三者中最大的
		int max = Math.max(X.value, Math.max(lData.max, rData.max));
		// 如果只考虑可能性一和可能性二，以X为头的子树的最大搜索二叉树大小
		int maxBSTSize = Math.max(lData.maxBSTSize, rData.maxBSTSize);
		// 如果只考虑可能性一和可能性二，以X为头的子树的最大搜索二叉树头节点
		Node maxBSTHead = lData.maxBSTSize >= rData.maxBSTSize ? lData.maxBSTHead
				: rData.maxBSTHead;
		// 利用收集的信息，可以判断是否存在可能性三
		if (lData.maxBSTHead == X.left && rData.maxBSTHead == X.right
				&& X.value > lData.max && X.value < rData.min) {
			maxBSTSize = lData.maxBSTSize + rData.maxBSTSize + 1;
			maxBSTHead = X;
		}
		// 信息全部搞定，返回
		return new ReturnType(maxBSTHead, maxBSTSize, min, max);
	}

	// for test -- print tree
	public static void printTree(Node head) {
		System.out.println("Binary Tree:");
		printInOrder(head, 0, "H", 17);
		System.out.println();
	}

	public static void printInOrder(Node head, int height, String to, int len) {
		if (head == null) {
			return;
		}
		printInOrder(head.right, height + 1, "v", len);
		String val = to + head.value + to;
		int lenM = val.length();
		int lenL = (len - lenM) / 2;
		int lenR = len - lenM - lenL;
		val = getSpace(lenL) + val + getSpace(lenR);
		System.out.println(getSpace(height * len) + val);
		printInOrder(head.left, height + 1, "^", len);
	}

	public static String getSpace(int num) {
		String space = " ";
		StringBuffer buf = new StringBuffer("");
		for (int i = 0; i < num; i++) {
			buf.append(space);
		}
		return buf.toString();
	}

	public static void main(String[] args) {

		Node head = new Node(6);
		head.left = new Node(1);
		head.left.left = new Node(0);
		head.left.right = new Node(3);
		head.right = new Node(12);
		head.right.left = new Node(10);
		head.right.left.left = new Node(4);
		head.right.left.left.left = new Node(2);
		head.right.left.left.right = new Node(5);
		head.right.left.right = new Node(14);
		head.right.left.right.left = new Node(11);
		head.right.left.right.right = new Node(15);
		head.right.right = new Node(13);
		head.right.right.left = new Node(20);
		head.right.right.right = new Node(16);

		printTree(head);
		Node bst = getMaxBST(head);
		printTree(bst);

	}

}

帖子的最高分数（假设答案法）

为了保证招聘信息的质量问题，公司为每个职位设计了打分系统，打分可以为正数，也可以为负数，正数表示用户认可帖子质量，负数表示用户不认可帖子质量．打分的分数根据评价用户的等级大小不定，比如可以为 -1分，10分，30分，-10分等。假设数组A记录了一条帖子所有打分记录，现在需要找出帖子曾经得到过最高的分数是多少，用于后续根据最高分数来确认需要对发帖用户做相应的惩罚或奖励．其中，最高分的定义为：用户所有打分记录中，连续打分数据之和的最大值即认为是帖子曾经获得的最高分。

例如：帖子10001010近期的打分记录为[1,1,-1,-10,11,4,-6,9,20,-10,-2],那么该条帖子曾经到达过的最高分数为11+4+(-6)+9+20=38。请实现一段代码，输入为帖子近期的打分记录，输出为当前帖子得到的最高分数。

思路：搞一个cur去遍历累加，如果cur<0了 让cur=0，然后用max记录最大值。

package class06;

public class Problem06_SubArrayMaxSum {

	public static int maxSum(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		int cur = 0;
		for (int i = 0; i != arr.length; i++) {
			cur += arr[i];
			max = Math.max(max, cur);
			cur = cur < 0 ? 0 : cur;
		}
		return max;
	}

	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int[] arr1 = { -2, -3, -5, 40, -10, -10, 100, 1 };
		System.out.println(maxSum(arr1));

		int[] arr2 = { -2, -3, -5, 0, 1, 2, -1 };
		System.out.println(maxSum(arr2));

		int[] arr3 = { -2, -3, -5, -1 };
		System.out.println(maxSum(arr3));

	}

}

子矩阵的最大累计和

给定一个整型矩阵，返回子矩阵的最大累计和

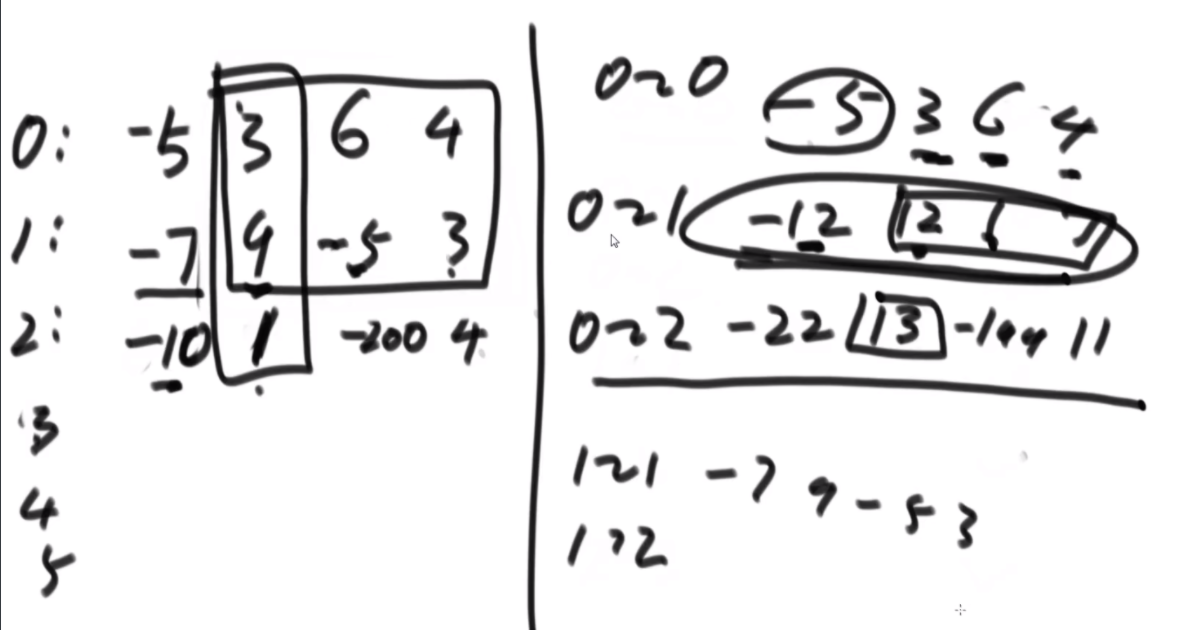
思路：利用压缩数组的思想，把二维数组搞到1维去，只需要把第一行累加到第二行就能代表整个两行3列的矩阵，然后穷尽，0-0，0-1，0-2，1-1，1-2，2-2。然后每一行的结果再去进行上一道题的累加（帖子的最高分数），就能求出最大的累加和。N行M列的，时间复杂度O(N²*M)

package class06;

public class Problem07_SubMatrixMaxSum {

	public static int maxSum(int[][] m) {
		if (m == null || m.length == 0 || m[0].length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		int cur = 0;
		int[] s = null;
		for (int i = 0; i != m.length; i++) {
			s = new int[m[0].length];
			for (int j = i; j != m.length; j++) {
				cur = 0;
				for (int k = 0; k != s.length; k++) {
					s[k] += m[j][k];
					cur += s[k];
					max = Math.max(max, cur);
					cur = cur < 0 ? 0 : cur;
				}
			}
		}
		return max;
	}

	public static void main(String[] args) {
		int[][] matrix = { { -90, 48, 78 }, { 64, -40, 64 }, { -81, -7, 66 } };
		System.out.println(maxSum(matrix));

	}

}

p24:

返回达标字符串的数量

字符串只由'0'和'1'两种字符构成，

当字符串长度为1时，所有可能的字符串为"0"、"1"；

当字符串长度为2时，所有可能的字符串为"00"、"01"、"10"、"11"；

当字符串长度为3时，所有可能的字符串为"000"、"001"、"010"、"011"、"100"、

"101"、"110"、"111"

...

如果某一个字符串中，只要是出现'0'的位置，左边就靠着'1'，这样的字符串叫作达标字符串。

给定一个正数N，返回所有长度为N的字符串中，达标字符串的数量。

比如，N=3，返回3，因为只有"101"、"110"、"111"达标。

思路：方法一：直接打表法，想一个暴力解，然后用打表法打印出来找规律，发现是斐波那契问题，直接优化完事。

方法二：如何理解这是斐波那契问题？假设给的数字是8，那么首字符一定是1，因此定义F(7)，F(i)就代表首字符是固定字符1，剩余字符是i-1个的情况。然后第一种情况假设第二个字符是1，那么可以直接加上F(i-1)，因为满足了固定字符即首字符为1的情况，第二种情况是第二个字符为0，那么第三个字符必须为1，因此可以直接加上F(i-2)，因为又是固定资福为1。即斐波那契问题。

去掉木棍阻止形成三角形

在迷迷糊糊的大草原上，小红捡到了n根木棍，第i根木棍的长度为i，小红现在很开心。想选出其中的三根木棍组成美丽的三角形。但是小明想捉弄小红，想去掉一些木棍，使得小红任意选三根木棍都不能组成三角形。

请问小明最少去掉多少根木棍呢？给定N，返回至少去掉多少根？

思路：直接就是只剩斐波那契个数的木棍，因为三角形要求两边之和大于第三遍，只要两边之和等于第三边，那么永远无法构成三角形，即斐波那契数列。

斐波那契优化套路

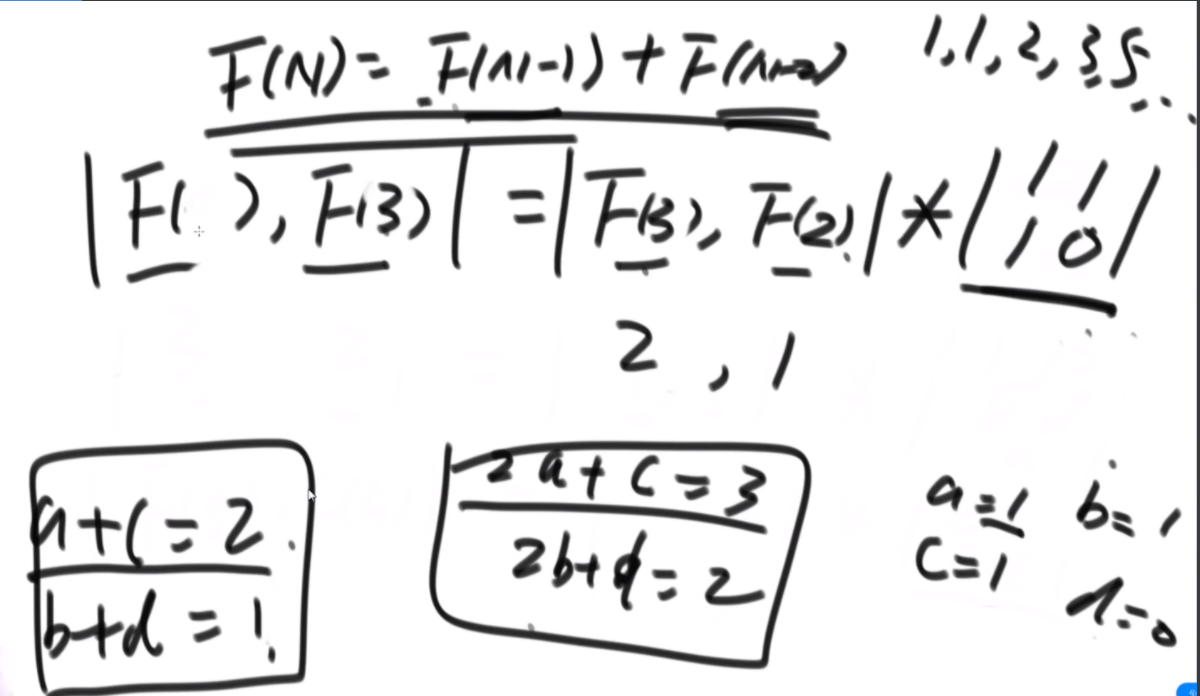
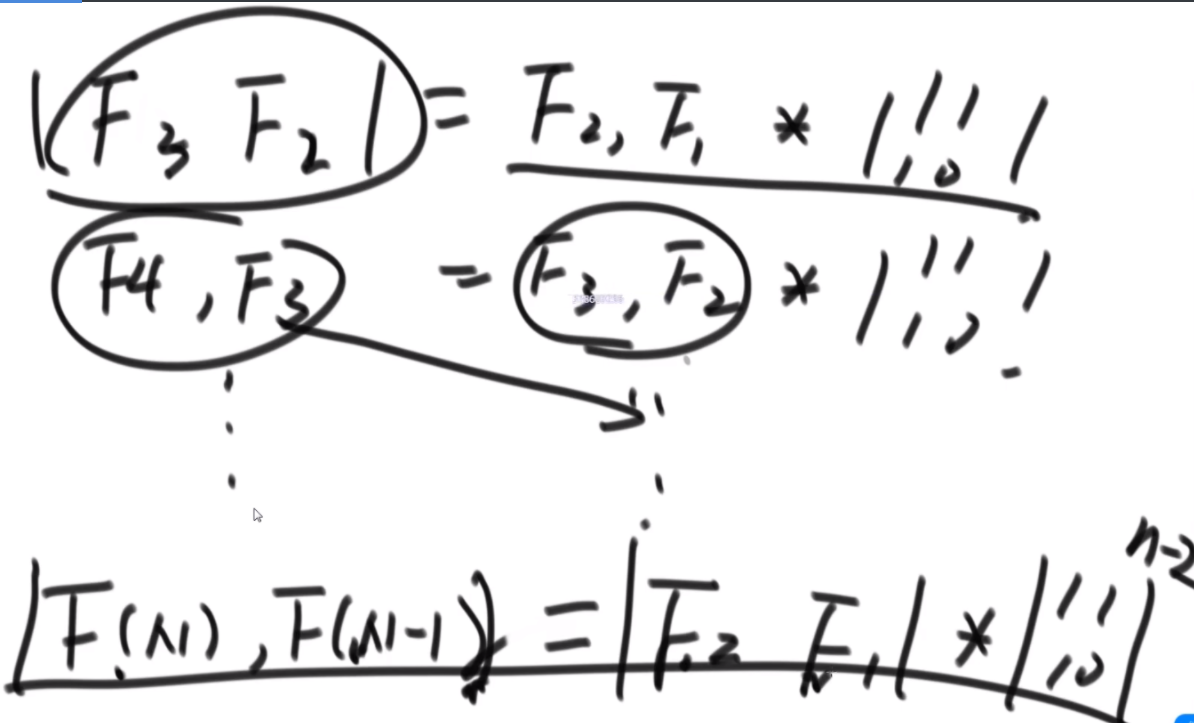
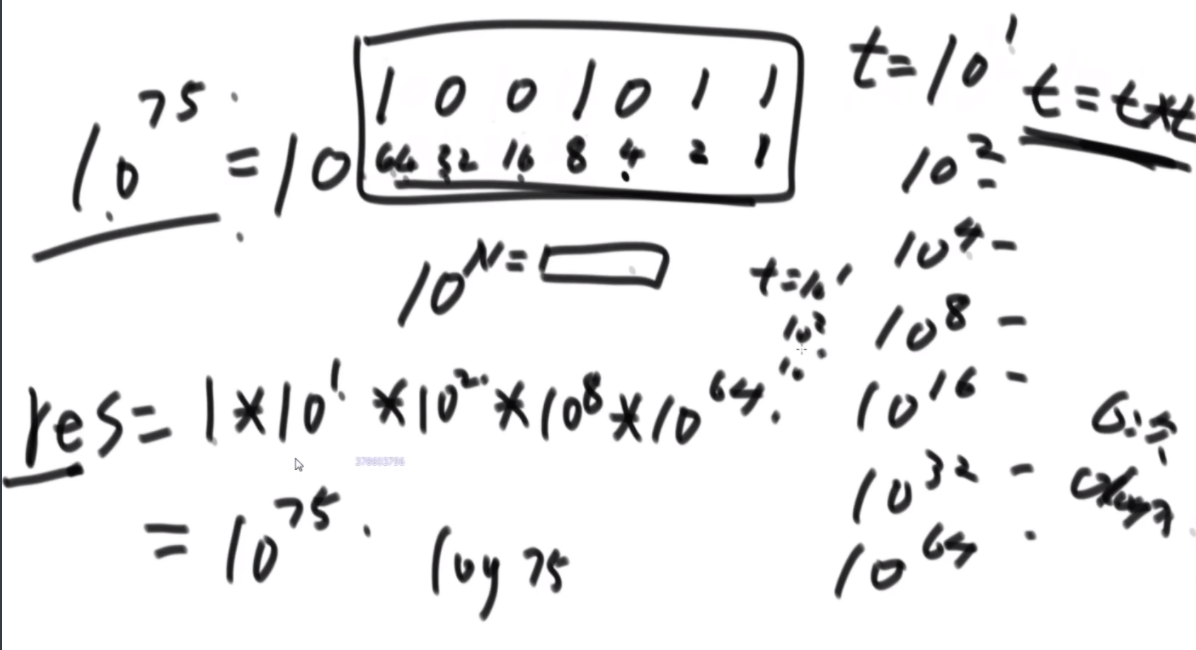
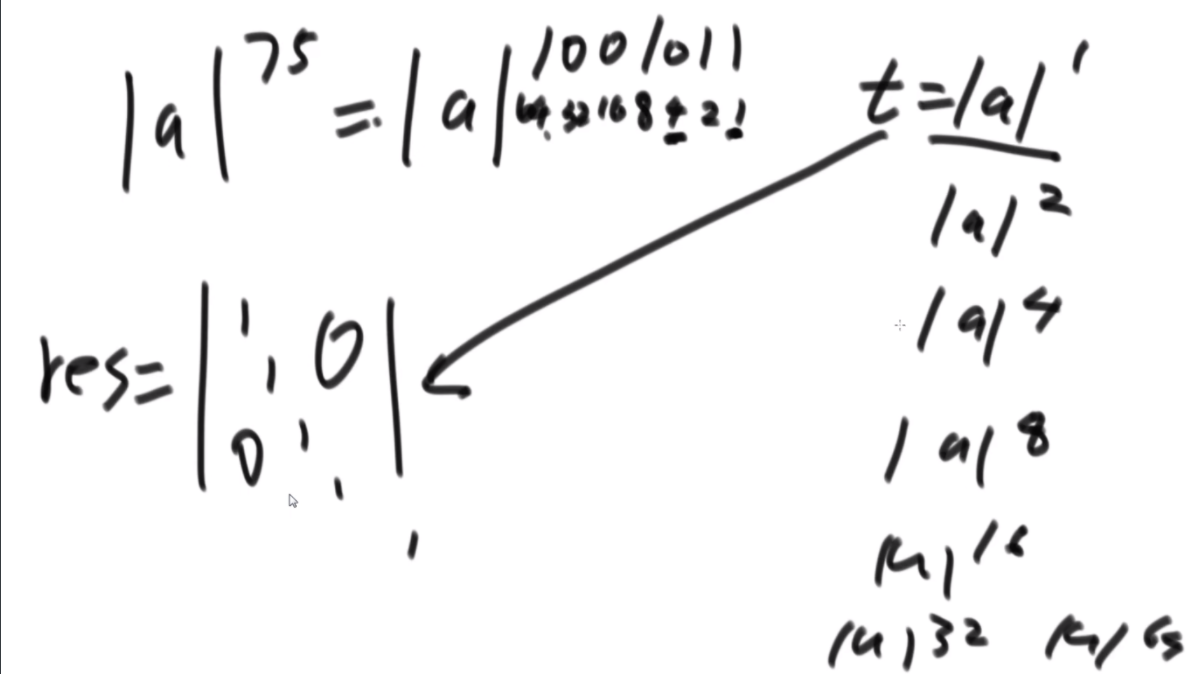
思路：由于斐波那契数列的要求是F(n) = F(n-1) + F(n-2)，这里最多减x就是x阶矩阵，最后是n-x次幂，斐波那契中x是2，有着固定的公式，那么根据线性代数可以将F(n)通过矩阵连乘的方式表示出来，然后矩阵的多少次幂可以根据求数字的多少次幂来推理得到，将次幂数转换成二进制的方式，从而完成优化，最终的时间复杂度为O(logn)，因为转换成了二进制，减少了很多不需要的次幂。

举例：假设农场母牛1只，一年能生一只，每只新牛3年后可以开始生牛，那么F(n)=F(n-1)（代表去年的牛都会活到今年，因为没有牛会死）+F(n-3)（代表3年前活着的那些牛，都会生出新牛），这就是3阶的矩阵，流程一样。

优化斐波那契的代码：

public static int getNum3(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2) {
			return 1;
		}
		//这个矩阵是手动算出来的
		int[][] base = { { 1, 1 }, { 1, 0 } };
		int[][] res = matrixPower(base, n - 2);
		return res[0][0] + res[1][0];
	}

	public static int[][] matrixPower(int[][] m, int p) {
		//res 单位矩阵
		int[][] res = new int[m.length][m[0].length];
		for (int i = 0; i < res.length; i++) {
			res[i][i] = 1;
		}
		int[][] t = m;
		for (; p != 0; p >>= 1) {
			if ((p & 1) != 0) {
				res = muliMatrix(res, t);
			}
			t = muliMatrix(t, t);
		}
		return res;
	}

	//O(1) 两个正方形矩阵相乘的结果返回
	public static int[][] muliMatrix(int[][] m1, int[][] m2) {
		int[][] res = new int[m1.length][m2[0].length];
		for (int i = 0; i < m1.length; i++) {
			for (int j = 0; j < m2[0].length; j++) {
				for (int k = 0; k < m2.length; k++) {
					res[i][j] += m1[i][k] * m2[k][j];
				}
			}
		}
		return res;
	}

背包里的零食放法数量

牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。

牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。

牛牛想知道在总体积不超过背包容量的情况下，他一共有多少种零食放法(总体积为0也算一种放法)。

思路：这个题很像p16讲的换钱的最少货币数，每一种零食可以选择放或者不放，然后可能性加起来，优化后放入dp表中，最后一行中小于等于背包体积的为正确解，加起来就行了

挑选合适的工作

为了找到自己满意的工作，牛牛收集了每种工作的难度和报酬。牛牛选工作的标准是在难度不超过自身能力值的情况下，牛牛选择报酬最高的工作。在牛牛选定了自己的工作后，牛牛的小伙伴们来找牛牛帮忙选工作，牛牛依然使用自己的标准来帮助小伙伴们。牛牛的小伙伴太多了，于是他只好把这个任务交给了你。

class Job { 
	public int money;// 该工作的报酬 
	public int hard; // 该工作的难度 
	public Job(int money, int hard) { 
		this.money = money; 
		this.hard = hard; 
	} 
}

给定一个Job类型的数组jobarr，表示所有的工作。给定一个int类型的数组arr，表示所有小伙伴的能力。 这里工作可以有无数人来，不会因为有人来而不能来了

返回int类型的数组，表示每一个小伙伴按照牛牛的标准选工作后所能获得的报酬。

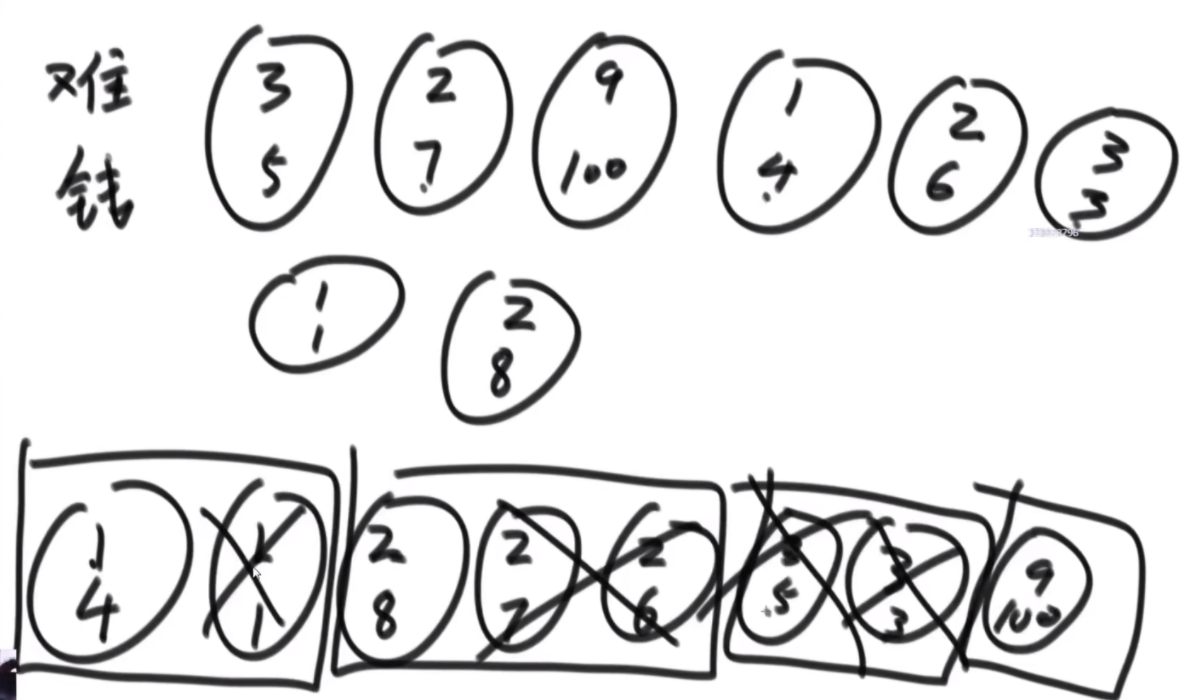
思路：这里利用到了有序表这一数据结构，当然我觉得这里更像是贪心，把这些工作按照难度从低到高排序，然后难度一样就钱从高到低排序，每个难度的分组里只要组长即难度相同给的钱最多的那个，其余的删掉。然后如果难度增加但是报酬不如低难度的工作也删掉，这样就形成了一个难度越高报酬越多的工作序列，每个人找到合适的难度就行了。

package class05;

import java.util.Arrays;
import java.util.Comparator;
import java.util.TreeMap;

public class Problem07_ChooseWork {

	public static class Job {
		public int money;
		public int hard;

		public Job(int money, int hard) {
			this.money = money;
			this.hard = hard;
		}
	}

	public static class JobComparator implements Comparator<Job> {
		@Override
		public int compare(Job o1, Job o2) {
			return o1.hard != o2.hard ? (o1.hard - o2.hard) : (o2.money - o1.money);
		}
	}

	public static int[] getMoneys(Job[] job, int[] ability) {
		Arrays.sort(job, new JobComparator());
		//难度为key的工作，最优钱数是多少，有序表
		TreeMap<Integer, Integer> map = new TreeMap<>();
		map.put(job[0].hard, job[0].money);
		Job pre = job[0];//pre之前组的组长
		for (int i = 1; i < job.length; i++) {
			if (job[i].hard != pre.hard && job[i].money > pre.money) {
				pre = job[i];
				map.put(pre.hard, pre.money);
			}
		}
		int[] ans = new int[ability.length];
		for (int i = 0; i < ability.length; i++) {
			Integer key = map.ceilingKey(ability[i]);
			ans[i] = key != null ? map.get(key) : 0;
		}
		return ans;
	}

	public static void main(String[] args) {
		TreeMap<Integer, Integer> map = new TreeMap<>();
		Integer key = map.ceilingKey(5);
		int test1 = key != null ? map.get(key) : 0;
		System.out.println(test1);
		System.out.println("====");
		int test2 = map.get(map.ceilingKey(5));
		System.out.println(test2);
	}

}

判断字符串为日常书写的数字

给定一个字符串，如果该字符串符合人们日常书写一个整数的形式，返回int类型的这个数；如果不符合或者越界返回-1或者报错。

思路：这种是业务驱动的题目，满足如上条件就成。

中间拼接数字过程选择用负数接的原因，负数范围比正数打一个，因此先用负数拼接，最后判断是否需要转正。

package class05;

public class Problem04_ConvertStringToInteger {

	public static int convert(String str) {
		if (str == null || str.equals("")) {
			return 0; // can not convert
		}
		char[] chas = str.toCharArray();
		if (!isValid(chas)) {
			return 0; // can not convert
		}
		boolean posi = chas[0] == '-' ? false : true;
		int minq = Integer.MIN_VALUE / 10;
		int minr = Integer.MIN_VALUE % 10;
		int res = 0;
		int cur = 0;
		for (int i = posi ? 0 : 1; i < chas.length; i++) {
			cur = '0' - chas[i];
			if ((res < minq) || (res == minq && cur < minr)) {
				return 0; // can not convert
			}
			res = res * 10 + cur;
		}
		if (posi && res == Integer.MIN_VALUE) {
			return 0; // can not convert
		}
		return posi ? -res : res;
	}

	public static boolean isValid(char[] chas) {
		if (chas[0] != '-' && (chas[0] < '0' || chas[0] > '9')) {
			return false;
		}
		if (chas[0] == '-' && (chas.length == 1 || chas[1] == '0')) {
			return false;
		}
		if (chas[0] == '0' && chas.length > 1) {
			return false;
		}
		for (int i = 1; i < chas.length; i++) {
			if (chas[i] < '0' || chas[i] > '9') {
				return false;
			}
		}
		return true;
	}

	public static void main(String[] args) {
		String test1 = "2147483647"; // max in java
		System.out.println(convert(test1));

		String test2 = "-2147483648"; // min in java
		System.out.println(convert(test2));

		String test3 = "2147483648"; // overflow
		System.out.println(convert(test3));

		String test4 = "-2147483649"; // overflow
		System.out.println(convert(test4));

		String test5 = "-123";
		System.out.println(convert(test5));

	}

}

p23:

实现狗猫队列结构

宠物、狗和猫的类如下:

public static class Pet { 
	private String type; 
	public Pet(String type) { 
		this.type = type; 
	}
	public String getPetType() {
    	return this.type;
    }
}
public static class Dog extends Pet {
	public Dog() {
		super("dog"); 
	} 
}
public static class Cat extends Pet {
	public Cat() {
		super("cat");
	} 
}

实现一种狗猫队列的结构，要求如下:

用户可以调用add方法将cat类或dog类的 实例放入队列中;

用户可以调用pollAll方法，将队列中所有的实例按照进队列 的先后顺序依次弹出;

用户可以调用pollDog方法，将队列中dog类的实例按照 进队列的先后顺序依次弹出;

用户可以调用pollCat方法，将队列中cat类的实 例按照进队列的先后顺序依次弹出;

用户可以调用isEmpty方法，检查队列中是 否还有dog或cat的实例;

用户可以调用isDogEmpty方法，检查队列中是否有dog 类的实例;

用户可以调用isCatEmpty方法，检查队列中是否有cat类的实例。

要求以上所有方法时间复杂度都是O(1)的

思路:搞一个count(时间戳)给每个pet对象，然后cat和dog继承pet，就每存入一个pet count++，然后从队列中获得pet的时候，比较猫和狗队列中队首的count值，小的那个先出，这样就保留了顺序，猫和狗自身的队列是没问题的。

package class04;

import java.util.LinkedList;
import java.util.Queue;

public class Problem01_DogCatQueue {

	public static class Pet {
		private String type;

		public Pet(String type) {
			this.type = type;
		}

		public String getPetType() {
			return this.type;
		}
	}

	public static class Dog extends Pet {
		public Dog() {
			super("dog");
		}
	}

	public static class Cat extends Pet {
		public Cat() {
			super("cat");
		}
	}

	public static class PetEnterQueue {
		private Pet pet;
		private long count;

		public PetEnterQueue(Pet pet, long count) {
			this.pet = pet;
			this.count = count;
		}

		public Pet getPet() {
			return this.pet;
		}

		public long getCount() {
			return this.count;
		}

		public String getEnterPetType() {
			return this.pet.getPetType();
		}
	}

	public static class DogCatQueue {
		private Queue<PetEnterQueue> dogQ;
		private Queue<PetEnterQueue> catQ;
		private long count;

		public DogCatQueue() {
			this.dogQ = new LinkedList<PetEnterQueue>();
			this.catQ = new LinkedList<PetEnterQueue>();
			this.count = 0;
		}

		public void add(Pet pet) {
			if (pet.getPetType().equals("dog")) {
				this.dogQ.add(new PetEnterQueue(pet, this.count++));
			} else if (pet.getPetType().equals("cat")) {
				this.catQ.add(new PetEnterQueue(pet, this.count++));
			} else {
				throw new RuntimeException("err, not dog or cat");
			}
		}

		public Pet pollAll() {
			if (!this.dogQ.isEmpty() && !this.catQ.isEmpty()) {
				if (this.dogQ.peek().getCount() < this.catQ.peek().getCount()) {
					return this.dogQ.poll().getPet();
				} else {
					return this.catQ.poll().getPet();
				}
			} else if (!this.dogQ.isEmpty()) {
				return this.dogQ.poll().getPet();
			} else if (!this.catQ.isEmpty()) {
				return this.catQ.poll().getPet();
			} else {
				throw new RuntimeException("err, queue is empty!");
			}
		}

		public Dog pollDog() {
			if (!this.isDogQueueEmpty()) {
				return (Dog) this.dogQ.poll().getPet();
			} else {
				throw new RuntimeException("Dog queue is empty!");
			}
		}

		public Cat pollCat() {
			if (!this.isCatQueueEmpty()) {
				return (Cat) this.catQ.poll().getPet();
			} else
				throw new RuntimeException("Cat queue is empty!");
		}

		public boolean isEmpty() {
			return this.dogQ.isEmpty() && this.catQ.isEmpty();
		}

		public boolean isDogQueueEmpty() {
			return this.dogQ.isEmpty();
		}

		public boolean isCatQueueEmpty() {
			return this.catQ.isEmpty();
		}

	}

	public static void main(String[] args) {
		DogCatQueue test = new DogCatQueue();

		Pet dog1 = new Dog();
		Pet cat1 = new Cat();
		Pet dog2 = new Dog();
		Pet cat2 = new Cat();
		Pet dog3 = new Dog();
		Pet cat3 = new Cat();

		test.add(dog1);
		test.add(cat1);
		test.add(dog2);
		test.add(cat2);
		test.add(dog3);
		test.add(cat3);

		test.add(dog1);
		test.add(cat1);
		test.add(dog2);
		test.add(cat2);
		test.add(dog3);
		test.add(cat3);

		test.add(dog1);
		test.add(cat1);
		test.add(dog2);
		test.add(cat2);
		test.add(dog3);
		test.add(cat3);
		while (!test.isDogQueueEmpty()) {
			System.out.println(test.pollDog().getPetType());
		}
		while (!test.isEmpty()) {
			System.out.println(test.pollAll().getPetType());
		}
	}

}

实现可以返回最小元素的栈

实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。

要求：1.pop、push、getMin操作的时间复杂度都是O(1)；2.设计的栈类型可以使用现成的栈结构

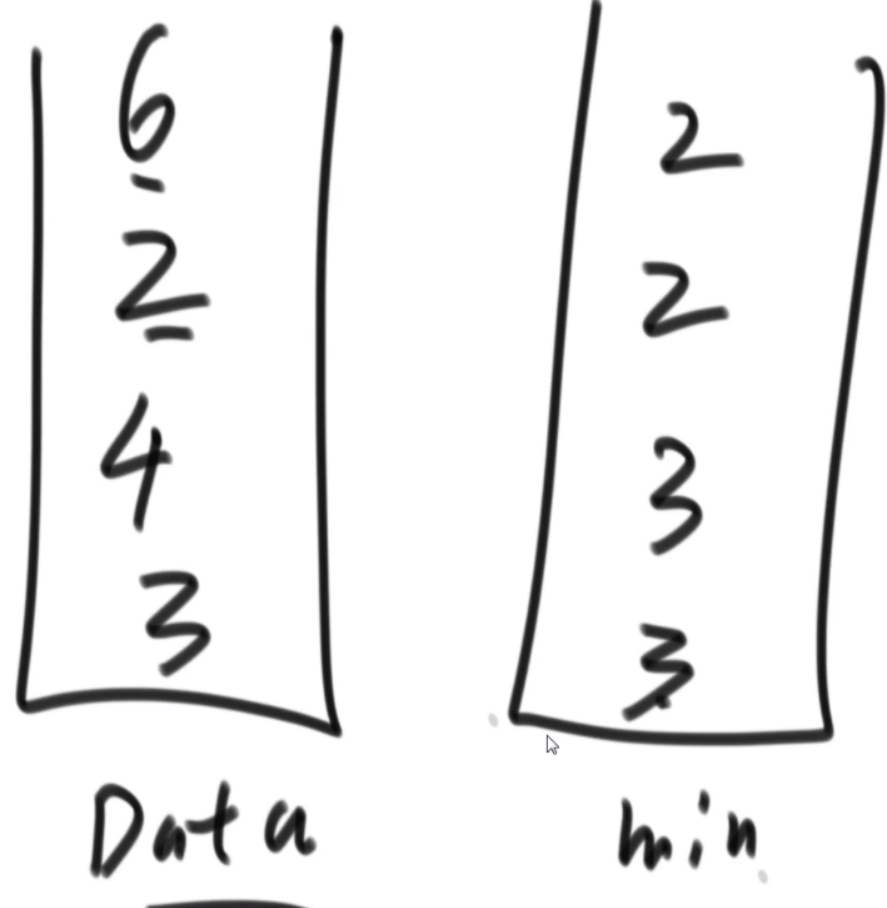
思路：搞一个放数据的栈，一个辅助栈，push的时候，push栈顶和要放入的元素中较小的那个，pop的时候两个栈一起pop，getMin就是辅助栈的栈顶。

package class04;

import java.util.Stack;

public class Problem02_GetMinStack {
	public static class MyStack1 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack1() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum <= this.getmin()) {
				this.stackMin.push(newNum);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			int value = this.stackData.pop();
			if (value == this.getmin()) {
				this.stackMin.pop();
			}
			return value;
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

	public static class MyStack2 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack2() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum < this.getmin()) {
				this.stackMin.push(newNum);
			} else {
				int newMin = this.stackMin.peek();
				this.stackMin.push(newMin);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			this.stackMin.pop();
			return this.stackData.pop();
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

	public static void main(String[] args) {
		MyStack1 stack1 = new MyStack1();
		stack1.push(3);
		System.out.println(stack1.getmin());
		stack1.push(4);
		System.out.println(stack1.getmin());
		stack1.push(1);
		System.out.println(stack1.getmin());
		System.out.println(stack1.pop());
		System.out.println(stack1.getmin());

		System.out.println("=============");

		MyStack1 stack2 = new MyStack1();
		stack2.push(3);
		System.out.println(stack2.getmin());
		stack2.push(4);
		System.out.println(stack2.getmin());
		stack2.push(1);
		System.out.println(stack2.getmin());
		System.out.println(stack2.pop());
		System.out.println(stack2.getmin());
	}

}

栈和队列的互相实现

栈实现队列

思路：搞两个栈，push的时候压入push栈，pop的时候如果pop栈为空，把push栈全部导入pop栈，如果不为空弹出pop栈栈顶元素。

队列实现栈

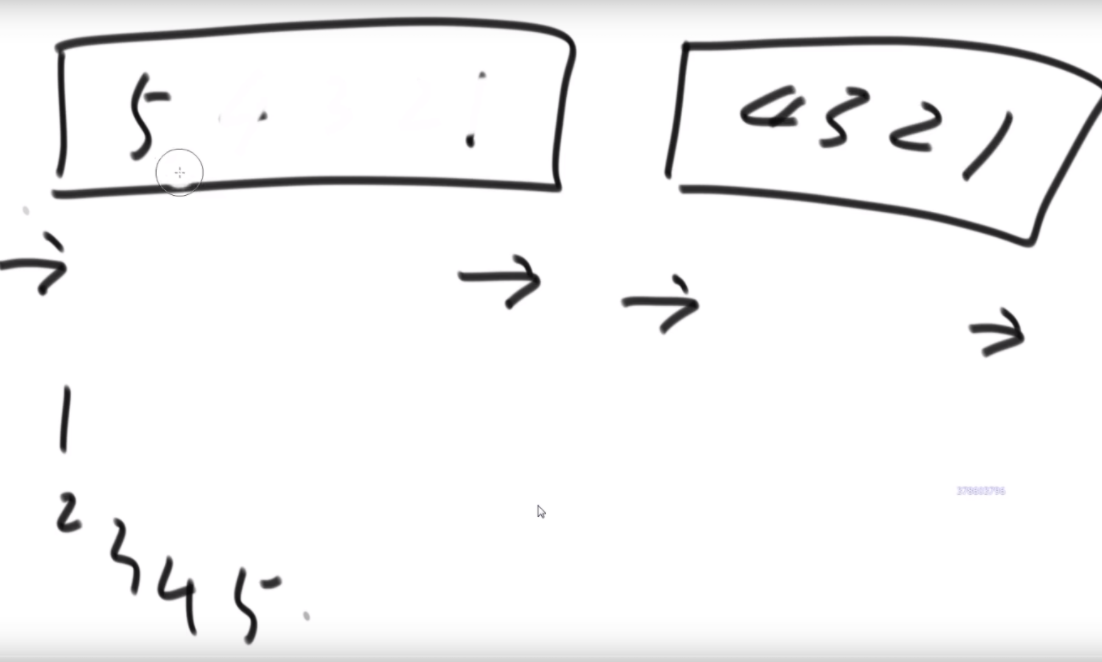
思路：搞两个队列，先依次push，然后pop的时候，把有数据的那个一直pop到size为1，即只剩一个元素，其他元素放入另一个，然后把剩下的这个元素返回给用户。

package class04;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class Problem03_StackAndQueueConvert {

	public static class TwoStacksQueue {
		private Stack<Integer> stackPush;
		private Stack<Integer> stackPop;

		public TwoStacksQueue() {
			stackPush = new Stack<Integer>();
			stackPop = new Stack<Integer>();
		}

		public void push(int pushInt) {
			stackPush.push(pushInt);
		}

		public int poll() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			} else if (stackPop.empty()) {
				while (!stackPush.empty()) {
					stackPop.push(stackPush.pop());
				}
			}
			return stackPop.pop();
		}

		public int peek() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			} else if (stackPop.empty()) {
				while (!stackPush.empty()) {
					stackPop.push(stackPush.pop());
				}
			}
			return stackPop.peek();
		}
	}

	public static class TwoQueuesStack {
		private Queue<Integer> queue;
		private Queue<Integer> help;

		public TwoQueuesStack() {
			queue = new LinkedList<Integer>();
			help = new LinkedList<Integer>();
		}

		public void push(int pushInt) {
			queue.add(pushInt);
		}

		public int peek() {
			if (queue.isEmpty()) {
				throw new RuntimeException("Stack is empty!");
			}
			while (queue.size() != 1) {
				help.add(queue.poll());
			}
			int res = queue.poll();
			help.add(res);
			swap();
			return res;
		}

		public int pop() {
			if (queue.isEmpty()) {
				throw new RuntimeException("Stack is empty!");
			}
			while (queue.size() > 1) {
				help.add(queue.poll());
			}
			int res = queue.poll();
			swap();
			return res;
		}

		private void swap() {
			Queue<Integer> tmp = help;
			help = queue;
			queue = tmp;
		}

	}

}

动态规划的空间压缩技巧

给你一个二维数组matrix，其中每个数都是正数，要求从左上角走到右下角。每一步只能向右或者向下，沿途经过的数字要累加起来。最后请返回最小的路径和。

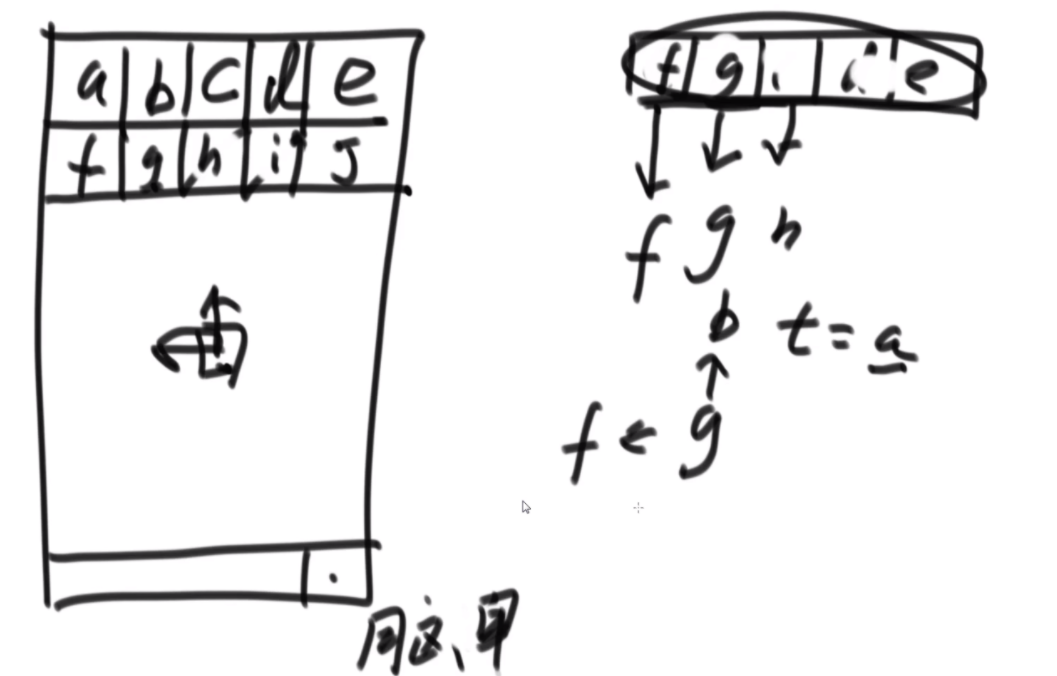
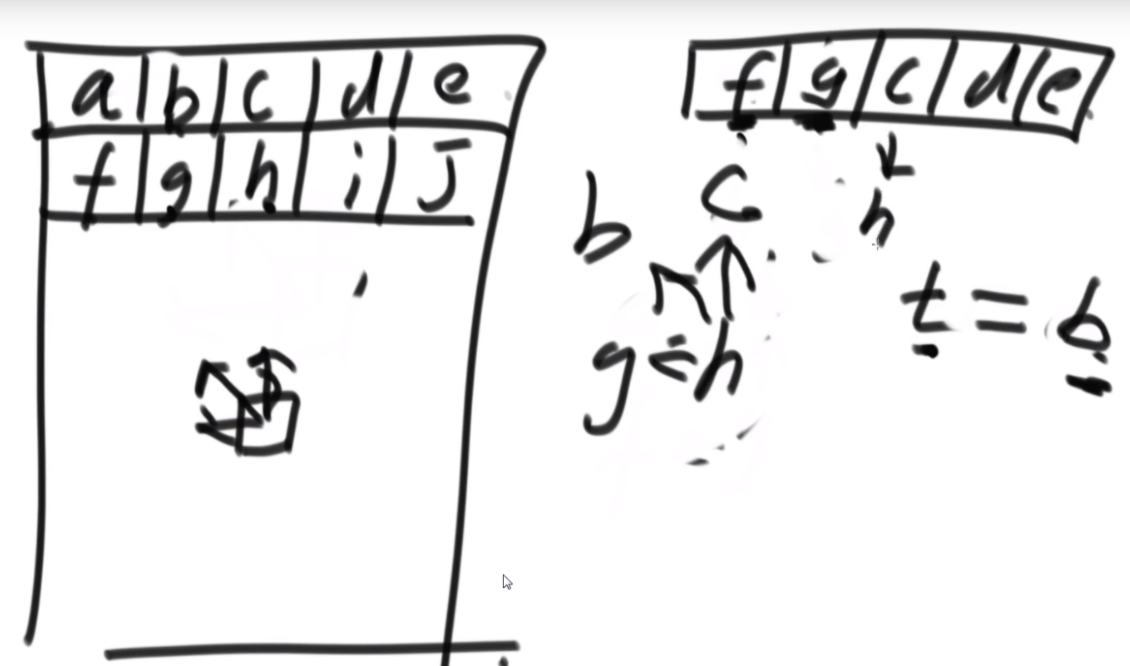
思路：假设它的依赖是左侧的一个和上侧的一个，动态规划的第一行一定是固定的生成的，然后第二行的第一个值f可以直接生成，因为它左边没有值，因此a直接变成f，b+f可以得到g，以此类推。假如是依赖上面三个值，那么可以从右侧开始生成，假如是依赖左侧和上面两个，那么可以搞一个变量，记住a，a变成f后，g的生成需要a、f、b，因此可以生成g，如果还需要更多元素，那么多申请俩变量记录一下就行了。

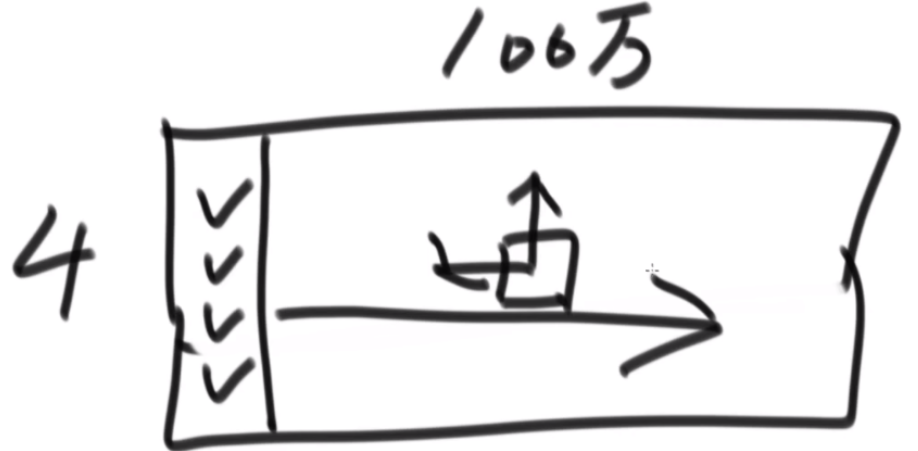
可以横着滚节省建立的数组空间。

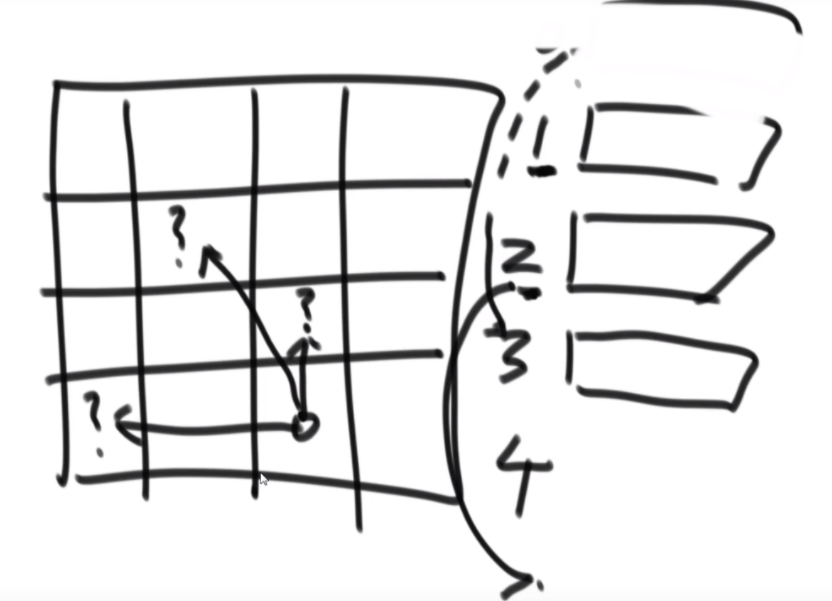
如果度太大，需要三个数组来回倒。

数组生成直方图装水

给定一个数组arr，已知其中所有的值都是非负的，将这个数组看作一个容器，请返回容器能装多少水

比如，arr = {3，1，2，5，2，4}，根据值画出的直方图就是容器形状，该容器可以装下5格水

再比如，arr = {4，5，1，3，2}，该容器可以装下2格水

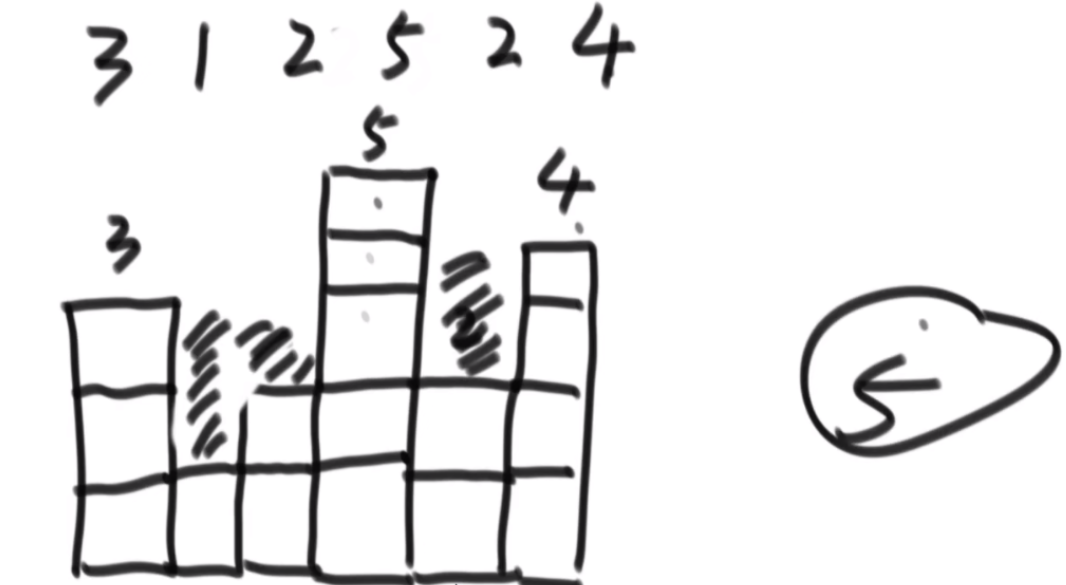
解释：将每个直方图横向拉伸，生成一个容器，能留下的雨水就是结果。

直接求解问题：会让每次求的小谷的计算浪费。

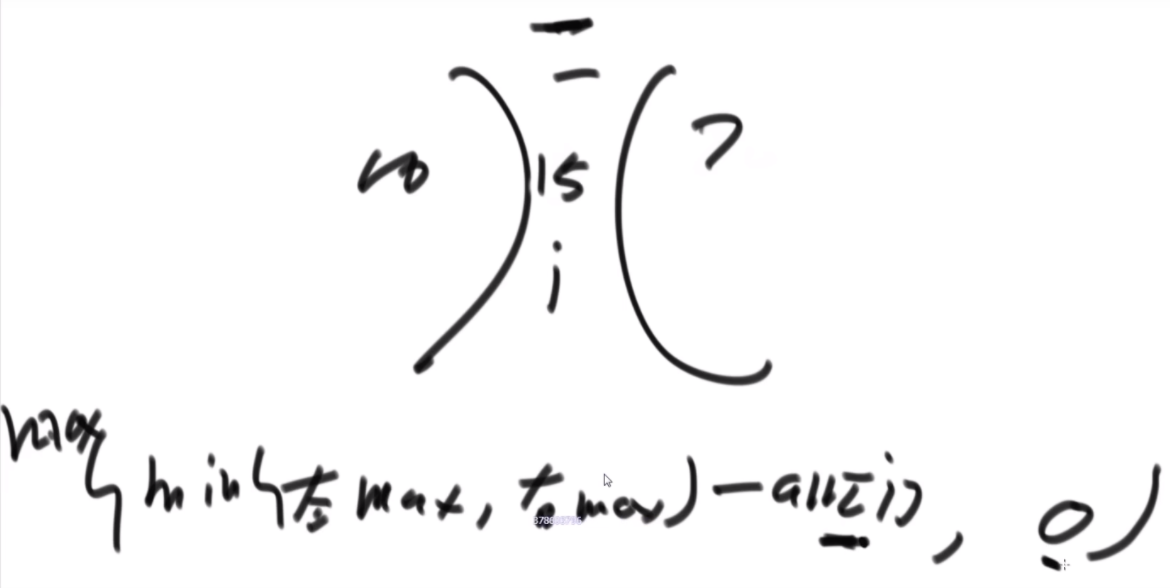
思路：有一点像洗衣机（打包）问题，从i位置看左右两侧的最大值，如果i小于左右两侧，那么可以留下水，水的体积为两者中较矮的那个-i的高度，如果i大于左右两侧，那么上一个可能的结果就为负数，如果为负数说明i最高，那么留不下水，留水的体积为0。

这里的首先思路是搞一个数组，去记录0-i位置的最大值，再搞一个数组，去记录i-n位置的最大值，然后遍历求解并且累加和完事。这种是O(n)的时间复杂度。

优化：

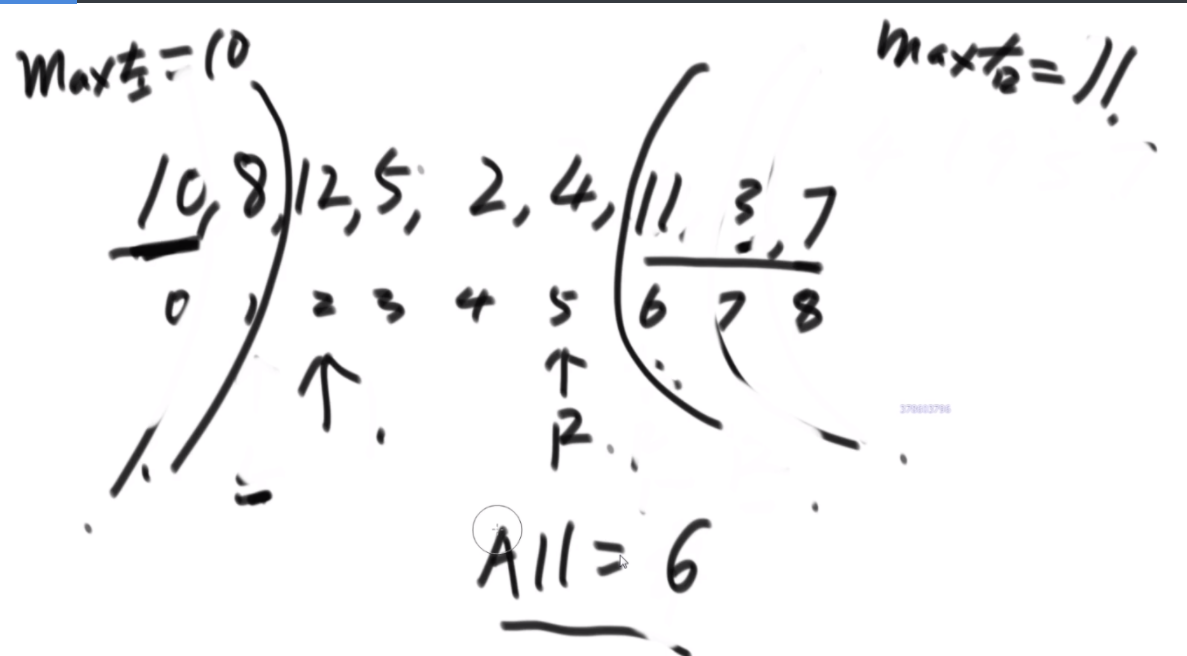
弄两个指针L,R，0位置和8位置直接是0，因为右侧没有高度一定留不下水，L到1，R到7，max左为10，max右为7，此时右边较小，直接更新R位置上的，然后R左移，如果左边较小就先更新左边的，如果一样大，先更新谁都行，达到节省数组空间的目的。

package class04;

import java.util.HashMap;
import java.util.Map.Entry;

public class Problem05_WaterProblem {

	public static int getWater1(int[] arr) {
		if (arr == null || arr.length < 3) {
			return 0;
		}
		int value = 0;
		for (int i = 1; i < arr.length - 1; i++) {
			int leftMax = 0;
			int rightMax = 0;
			for (int l = 0; l < i; l++) {
				leftMax = Math.max(arr[l], leftMax);
			}
			for (int r = i + 1; r < arr.length; r++) {
				rightMax = Math.max(arr[r], rightMax);
			}
			value += Math.max(0, Math.min(leftMax, rightMax) - arr[i]);
		}
		return value;
	}

	public static int getWater2(int[] arr) {
		if (arr == null || arr.length < 3) {
			return 0;
		}
		int n = arr.length - 2;
		int[] leftMaxs = new int[n];
		leftMaxs[0] = arr[0];
		for (int i = 1; i < n; i++) {
			leftMaxs[i] = Math.max(leftMaxs[i - 1], arr[i]);
		}
		int[] rightMaxs = new int[n];
		rightMaxs[n - 1] = arr[n + 1];
		for (int i = n - 2; i >= 0; i--) {
			rightMaxs[i] = Math.max(rightMaxs[i + 1], arr[i + 2]);
		}
		int value = 0;
		for (int i = 1; i <= n; i++) {
			value += Math.max(0, Math.min(leftMaxs[i - 1], rightMaxs[i - 1]) - arr[i]);
		}
		return value;
	}

	public static int getWater3(int[] arr) {
		if (arr == null || arr.length < 3) {
			return 0;
		}
		int n = arr.length - 2;
		int[] rightMaxs = new int[n];
		rightMaxs[n - 1] = arr[n + 1];
		for (int i = n - 2; i >= 0; i--) {
			rightMaxs[i] = Math.max(rightMaxs[i + 1], arr[i + 2]);
		}
		int leftMax = arr[0];
		int value = 0;
		for (int i = 1; i <= n; i++) {
			value += Math.max(0, Math.min(leftMax, rightMaxs[i - 1]) - arr[i]);
			leftMax = Math.max(leftMax, arr[i]);
		}
		return value;
	}

	public static int getWater4(int[] arr) {
		if (arr == null || arr.length < 3) {
			return 0;
		}
		int value = 0;
		int leftMax = arr[0];
		int rightMax = arr[arr.length - 1];
		int l = 1;
		int r = arr.length - 2;
		while (l <= r) {
			if (leftMax <= rightMax) {
				value += Math.max(0, leftMax - arr[l]);
				leftMax = Math.max(leftMax, arr[l++]);
			} else {
				value += Math.max(0, rightMax - arr[r]);
				rightMax = Math.max(rightMax, arr[r--]);
			}
		}
		return value;
	}

	public static int[] generateRandomArray() {
		int[] arr = new int[(int) (Math.random() * 98) + 2];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) (Math.random() * 200) + 2;
		}
		return arr;
	}

	public static void main(String[] args) {
		for (int i = 0; i < 1000000; i++) {
			int[] arr = generateRandomArray();
			int r1 = getWater1(arr);
			int r2 = getWater2(arr);
			int r3 = getWater3(arr);
			int r4 = getWater4(arr);
			if (r1 != r2 || r3 != r4 || r1 != r3) {
				System.out.println("What a fucking day! fuck that! man!");
			}
		}
		
		HashMap<String,String> map = new HashMap<String,String>();
		
        for(Entry<String,String> entry : map.entrySet()){
            System.out.println(entry.getKey()+" , "+ entry.getValue());
        }
		
	}

}

最大左侧最大值减右侧最大值

给定一个数组arr长度为N，你可以把任意长度大于0且小于N的前缀作为左部分，剩下的作为右部分。但是每种划分下都有左部分的最大值和右部分的最大值，请返回最大的，左部分最大值减去右部分最大值的绝对值。

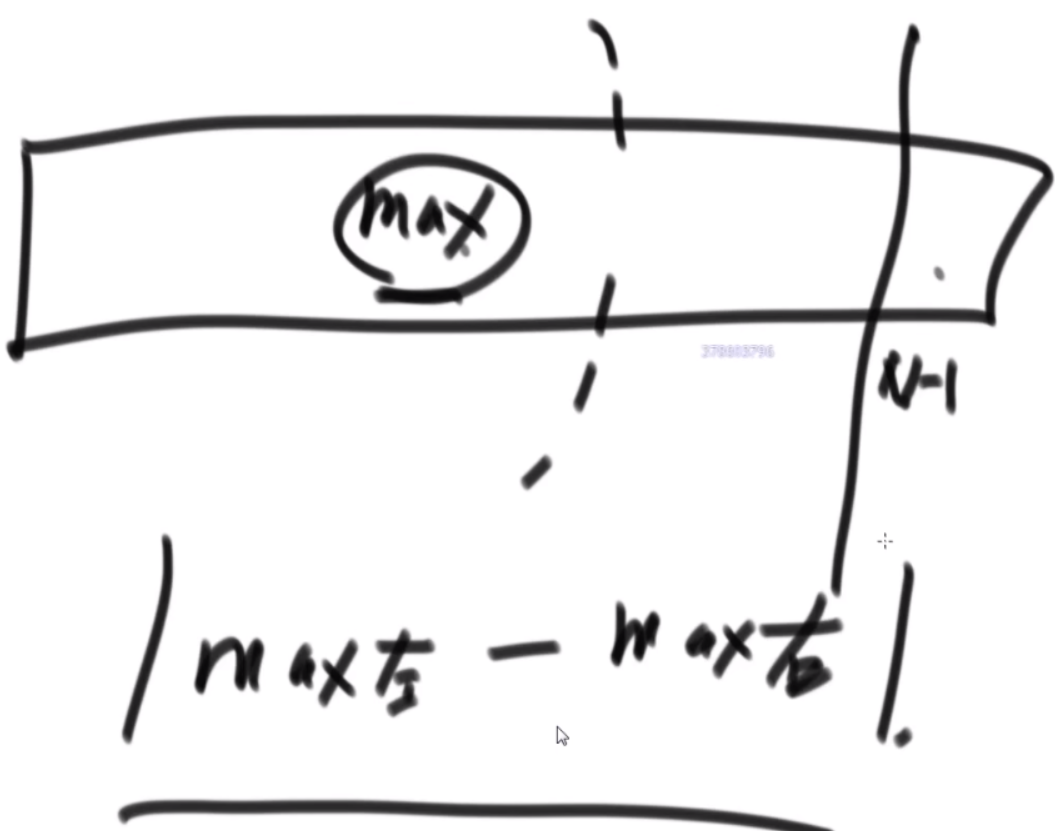
思路：arr中一定有一个最大值，假设这个max在左侧，那么如何使右侧的最大值最小呢？那么就是切一刀，只留下最后一个元素，（解释：如果有更多元素，假设最末尾元素是这些中最大的，那么多不多无所谓；假设末尾元素不是最大的，那么右侧的最大值就因为多出来的元素变大了，因此选择只要一个元素）。结论：找到最大值，看看是减最左侧的大还是减最右侧的大，最大的绝对值就是结果。

判断是否互为旋转词

如果一个字符串为str，把字符串str前面任意的部分挪到后面形成的字符串叫作str的旋转词。比如str="12345"，str的旋转词有"12345"、"23451"、"34512"、"45123"和"51234"。给定两个字符串a和b，请判断a和b是否互为旋转词。

比如：

a="cdab"，b="abcd"，返回true。

a="1ab2"，b="ab12"，返回false。

a="2ab1"，b="ab12"，返回true。

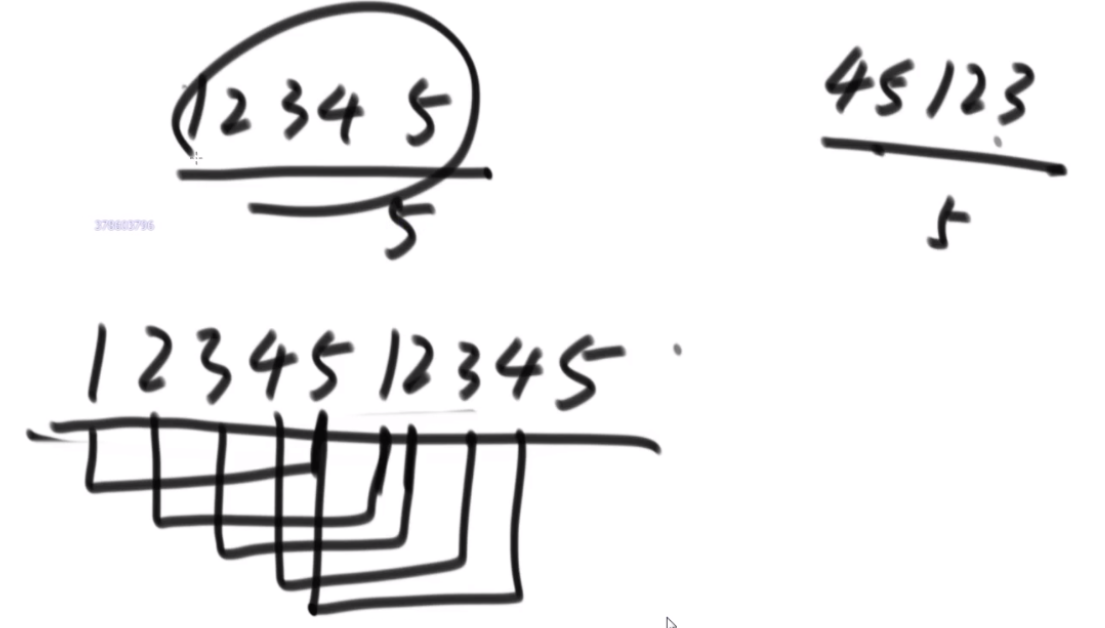
思路：把这个 字符串拼一次自己，然后看要判断的字符串是不是这个串的子串，如果是的话一定是旋转词，这个拼接后的字符串已经穷举了旋转词的所有可能，然后查找子串用到的就是KMP算法，去搞一个前缀长度的数组去搞。

喝咖啡洗杯子问题

题目要求：这道题是京东原题第四题，总共五道写出两道就可以进面试。arr数组中长度是咖啡机的数量，每个位置元素代表每个咖啡机泡一杯咖啡所需要的时间，假设每个人拿到咖啡后都是瞬间喝完，N代表要喝咖啡的人数，a代表我们有一台洗杯子的机器，这个机器需要a个单位时间去洗干净杯子，b代表杯子不去用机器直接挥发到干净所需要的时间。

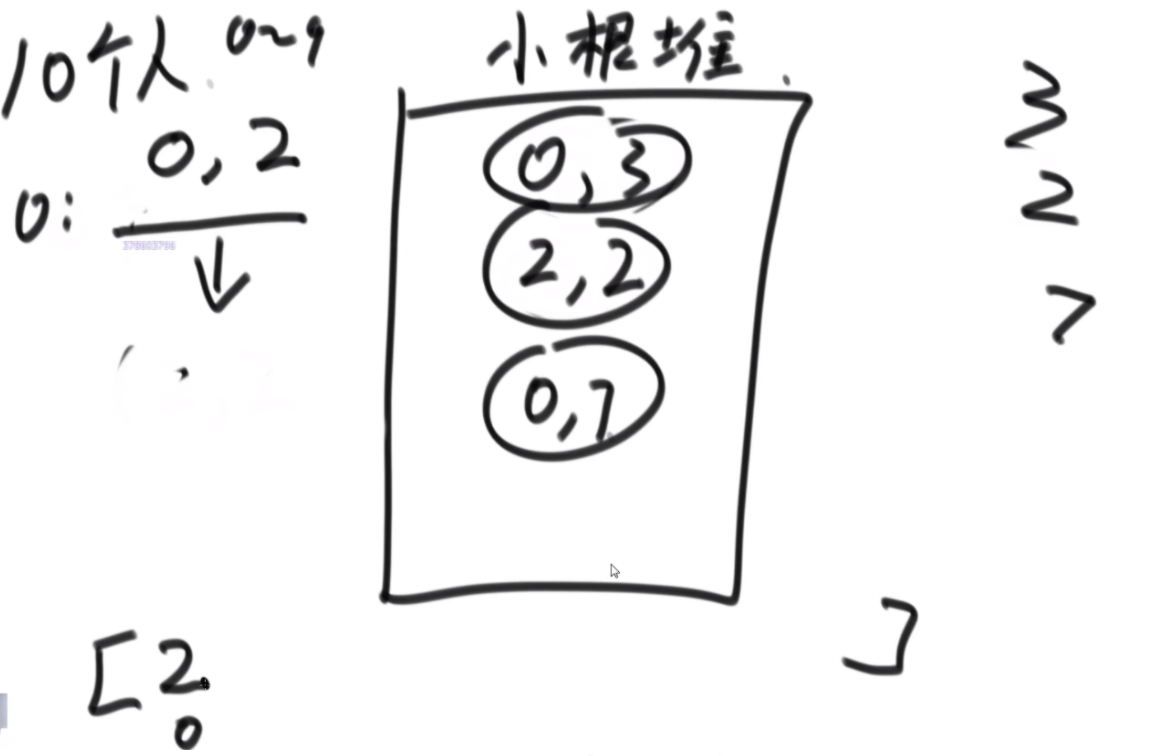
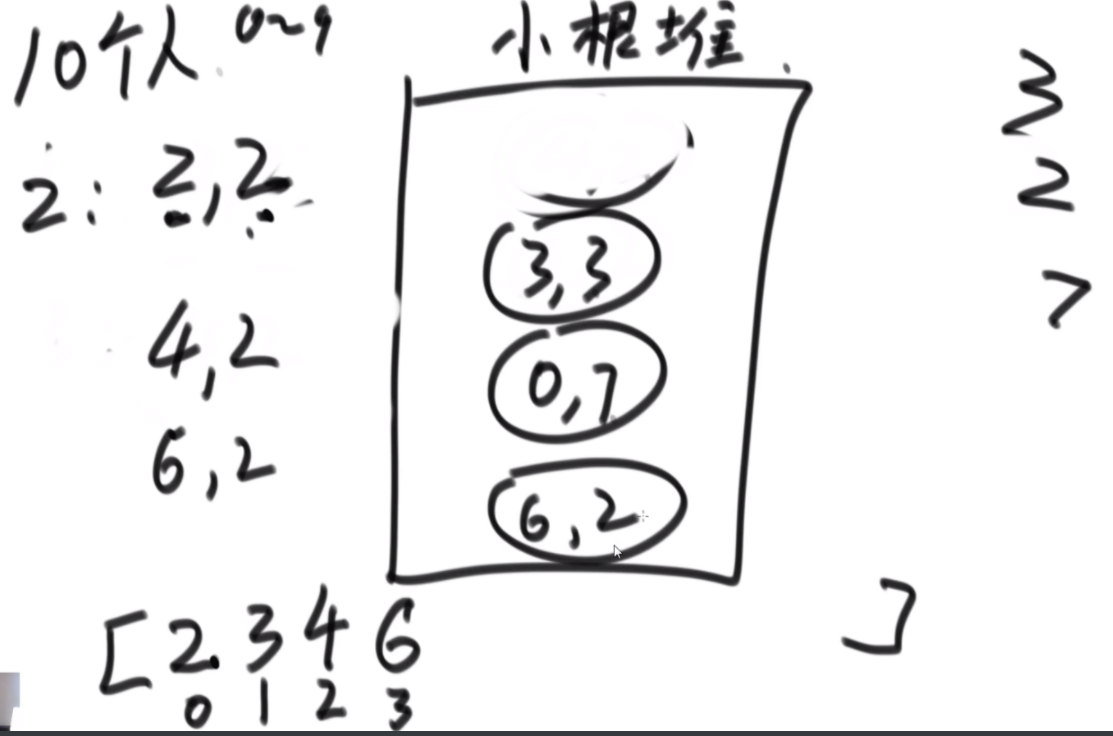
喝咖啡的贪心算法：构造一个小根堆，里面的元素是每个咖啡机，左边的数字代表可以使用的时间，初始都是0，右边的数字代表泡一杯咖啡需要多久，这个小根堆的比较方法是这两个数字加起来的和从小到大排序。每次取堆顶来用，然后把两个数相加作为左边的数再放进去，这个贪心代表着每次选择最早能获得一杯咖啡的时间。

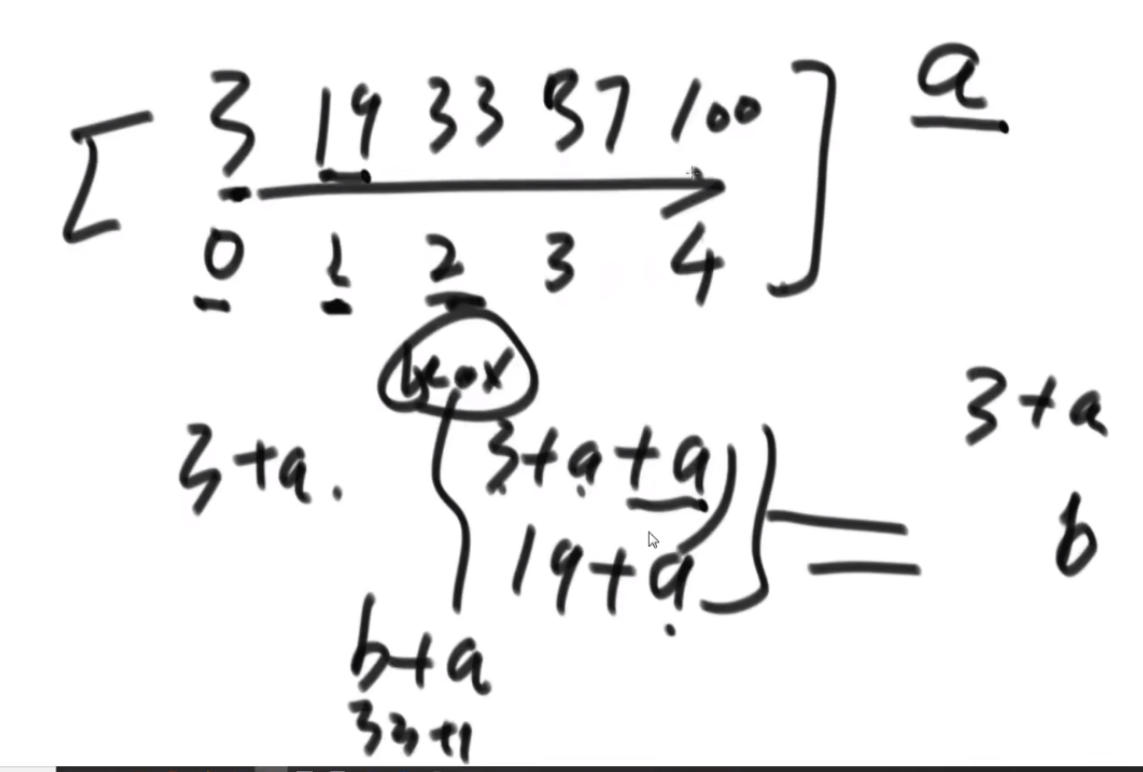
估计washline的最大值：我们想要获得最晚的咖啡机的使用时间，这样我们的动态规划优化过程中使用的数组才不会越界，下面是优化后的代码。（懒得打了，下次一定）

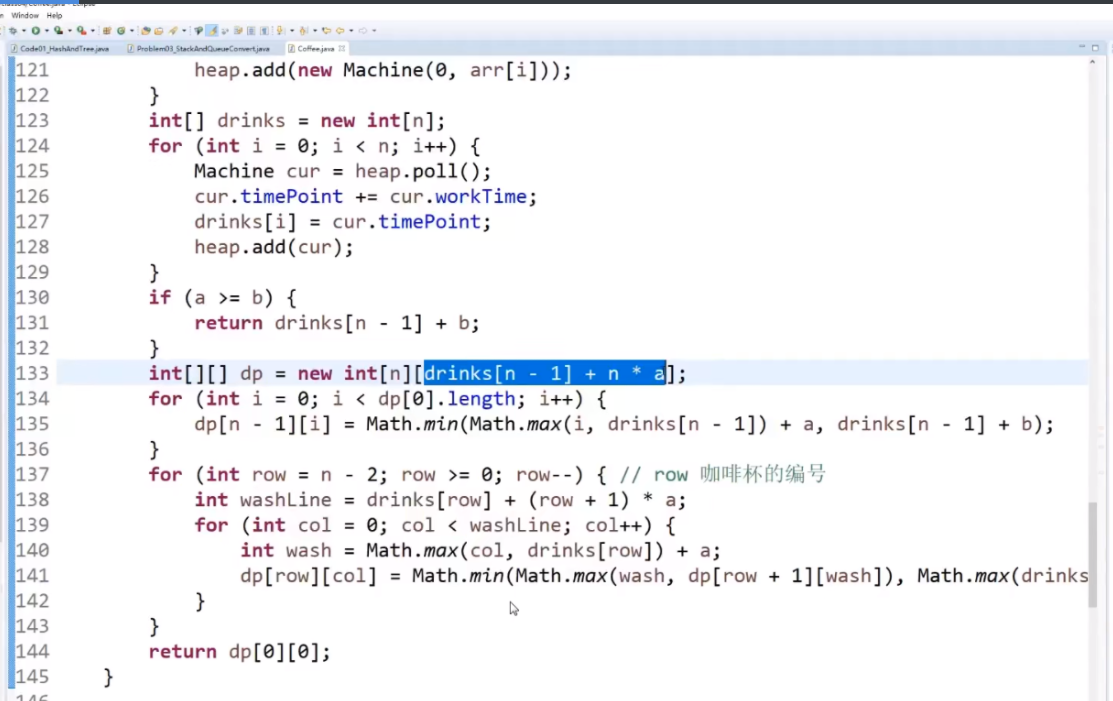
动态规划的洗杯子：见代码注释

package ZuoShen2.ZhongClass02;

import java.util.Comparator;
import java.util.PriorityQueue;

public class CoffeeGlasses {

    //方法二：稍微好一点的解法
    public static class Machine{
        public int timePoint;
        public int workTime;

        public Machine(int t,int w){
            timePoint=t;
            workTime=w;
        }
    }

    public static class MachineComparator implements Comparator<Machine> {
        @Override
        public int compare(Machine o1,Machine o2) {
            return (o1.timePoint+o1.workTime)-(o2.timePoint+o2.workTime);
        }
    }

    //方法二，每个人暴力尝试每一个咖啡机给自己做咖啡，优化成贪心
    public static int minTime(int[] arr,int n,int a,int b){
        PriorityQueue<Machine> heap = new PriorityQueue<>(new MachineComparator());
        for (int i = 0; i < arr.length; i++) {
            heap.add(new Machine(0,arr[i]));
        }
        int[] drinks = new int[n];
        for (int i = 0; i < n; i++) {
            Machine cur = heap.poll();
            cur.timePoint += cur.workTime;
            drinks[i] = cur.timePoint;
            heap.add(cur);
        }
        return process(drinks,a,b,0,0);
    }


    //洗杯子的过程  调用：return process(drinks,a,b,0,0);
    //假设洗咖啡杯的机器，在washLine的时间才有空
    //a 洗杯子的机器洗一杯的时间
    //b 咖啡杯子自然挥发的时间
    //如果要洗完drinks[index...N-1]，返回最早完成所有事情的时间点
    //方法二，洗咖啡杯的方式和原来一样，知识这个暴力版本减少了一个可变参数
    public static int process(int[] drinks,int a,int b,int index,int washLine){
        if(index==drinks.length-1){  //只剩最后一个杯子了
            return Math.min(Math.max(washLine,drinks[index])+a,drinks[index]+b);
        }
        //wash是当前的咖啡杯，决定放到洗咖啡的机器里去洗，什么时候能洗完
        int wash = Math.max(washLine,drinks[index])+a;
        //洗完剩下所有的咖啡杯最早的结束时间
        int next1 = process(drinks,a,b,index+1,wash);
        //就是我用机器洗的时候，其它杯子想洗的话只能自然烘干，万一后面的自然烘干比我洗的还快那最后答案就是我洗完的时间
        int p1 = Math.max(wash,next1);

        //dry是当前的咖啡杯，决定自然晾干，什么时候能洗完
        int dry = drinks[index]+b;
        int next2 = process(drinks,a,b,index+1,washLine);
        int p2 = Math.max(dry,next2);
        return Math.min(p1,p2);
    }


}

调整相邻数字相乘是4的倍数

给定一个数组arr，如果通过调整可以做到arr中任意两个相邻的数字相乘是4的倍数，返回true；如果不能返回false。

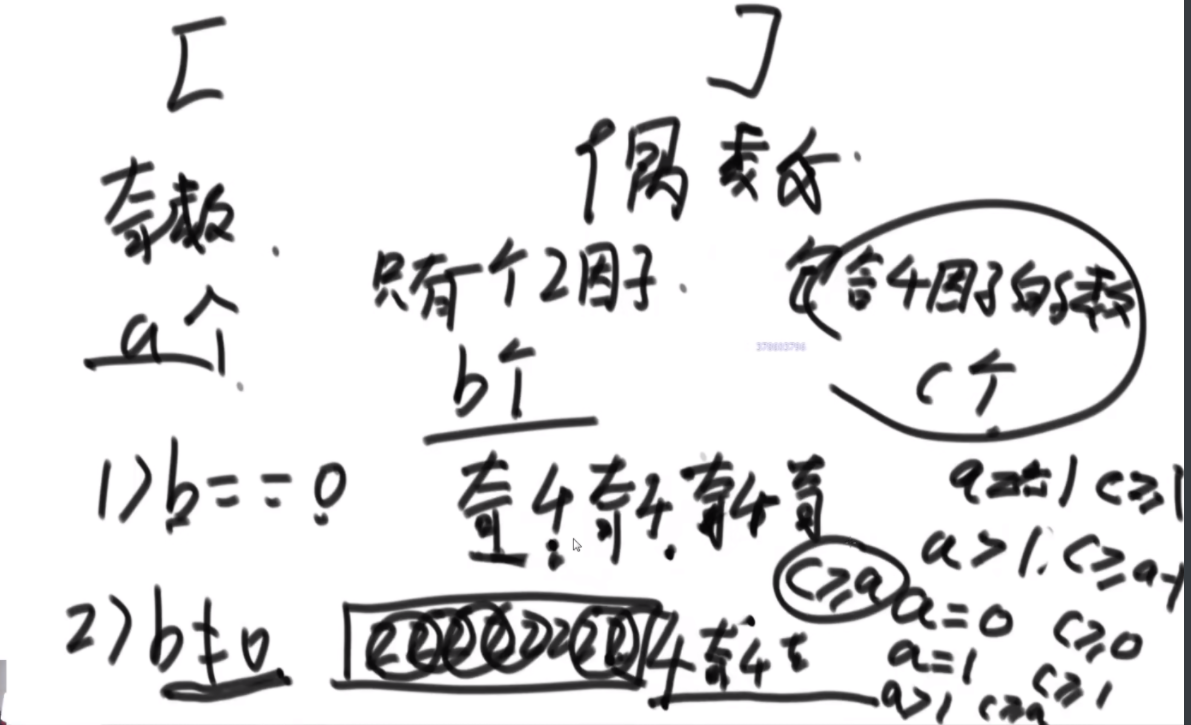
思路：如上图，差不多第二题的难度，都不想多解释hhh，跟咖啡机比好简单。

？？？？隔了好多天来看 md啥也不是

p22:

洗衣机问题（打包机问题）

有n个打包机器从左到右一字排开，上方有一个自动装置会抓取一批放物品到每个打包机上，放到每个机器上的这些物品数量有多有少，由于物品数量不相同，需要工人将每个机器上的物品进行移动从而到达物品数量相等才能打包。每个物品重量太大、每次只能搬一个物品进行移动，为了省力，只在相邻的机器上移动。请计算在搬动最小轮数的前提下，使每个机器上的物品数量相等。如果不能使每个机器上的物品相同，返回-1。

例如[1,0,5]表示有3个机器，每个机器上分别有1、0、5个物品，经过这些轮后：

第一轮：1 0 <- 5 => 1 1 4

第二轮：1 <-1<- 4 => 2 1 3

第三轮： 2 1 <- 3 => 2 2 2

移动了3轮，每个机器上的物品相等，所以返回3

例如[2,2,3]表示有3个机器，每个机器上分别有2、2、3个物品，这些物品不管怎么移动，都不能使三个机器上物品数量相等，返回-1

思路：

1. 先把总数%机器数量看是否为0，即是否整除，如果不能的话直接GG。
2. 从中间i位置分开，把左右两边看成整体，计算左边有多少个位置，那么左边应有多少个包裹，多出来的转移到右边，不够的从右边转移。
3. 如果左右两边都缺少包裹。都是负数，那么肯定是i位置太多了，移动位置至少是左右需要的包裹和。
4. 如果左右两边都不缺少包裹。都是正数，那么至少是左右包裹绝对值最大的次数。？？

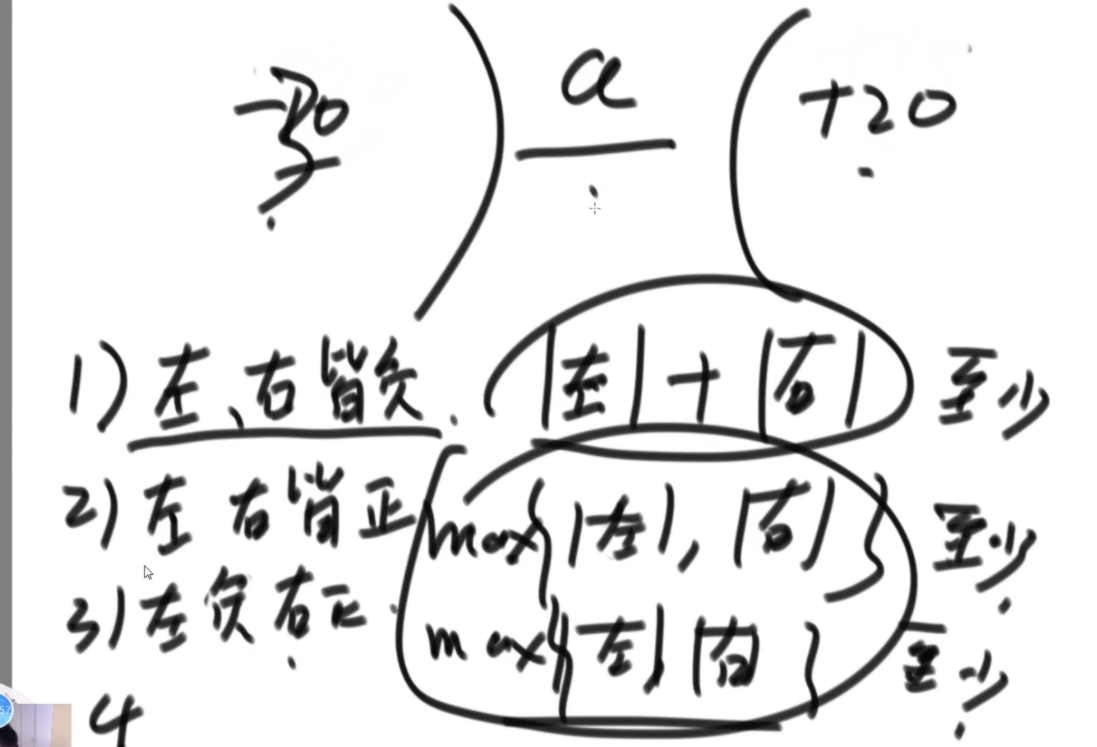
由上面可以推出一个结论，每个点算出一个答案，最大的点就是答案。

package ZuoShen2.ZhongClass02;

public class PackingMachine {
    public static int MinOps(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int size = arr.length;
        int sum = 0;
        for (int i = 0; i < size; i++) {
            sum += arr[i];
        }
        if (sum % size != 0) {
            return -1;
        }
        int avg = sum / size;
        int leftSum = 0; //左侧已经遍历过的累加和
        int ans = 0; //结果
        for (int i = 0; i < arr.length; i++) {
            //正 需要输入  负 需要输出
            int L = i * avg - leftSum;
            //正 需要输入  负 需要输出
            int R = (size - i - 1) * avg - (sum - leftSum - arr[i]);
            if (L > 0 && R > 0) {
                ans = Math.max(ans, Math.abs(L) + Math.abs(R));
            } else {
                ans = Math.max(ans, Math.max(Math.abs(L), Math.abs(R)));
            }
            leftSum += arr[i];
        }
        return ans;
    }

    public static void main(String[] args) {

    }
}

zigzag方式打印矩阵

用zigzag的方式打印矩阵，比如如下的矩阵

0 1 2 3

4 5 6 7

8 9 10 11

打印顺序为：0 1 4 8 5 2 3 6 9 10 7 11

思路：

搞两个变量A,B，然后A逐渐往右走，B逐渐往下走，只要他俩在同一个斜线，就从左下打印到右上或者反过来，这个通过一个boolean控制。A走到最右边就往下走，B走到最下边往右走，同理。

package class03;

public class Problem02_ZigZagPrintMatrix {

	public static void printMatrixZigZag(int[][] matrix) {
		int tR = 0;
		int tC = 0;
		int dR = 0;
		int dC = 0;
		int endR = matrix.length - 1;
		int endC = matrix[0].length - 1;
		boolean fromUp = false;
		while (tR != endR + 1) {
			printLevel(matrix, tR, tC, dR, dC, fromUp);
			tR = tC == endC ? tR + 1 : tR;
			tC = tC == endC ? tC : tC + 1;
			dC = dR == endR ? dC + 1 : dC;
			dR = dR == endR ? dR : dR + 1;
			fromUp = !fromUp;
		}
		System.out.println();
	}

	public static void printLevel(int[][] m, int tR, int tC, int dR, int dC,
			boolean f) {
		if (f) {
			while (tR != dR + 1) {
				System.out.print(m[tR++][tC--] + " ");
			}
		} else {
			while (dR != tR - 1) {
				System.out.print(m[dR--][dC++] + " ");
			}
		}
	}

	public static void main(String[] args) {
		int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
		printMatrixZigZag(matrix);

	}

}

用螺旋的方式打印矩阵

用螺旋的方式打印矩阵，比如如下的矩阵

0 1 2 3

4 5 6 7

8 9 10 11

打印顺序为：0 1 2 3 7 11 10 9 8 4 5 6

思路：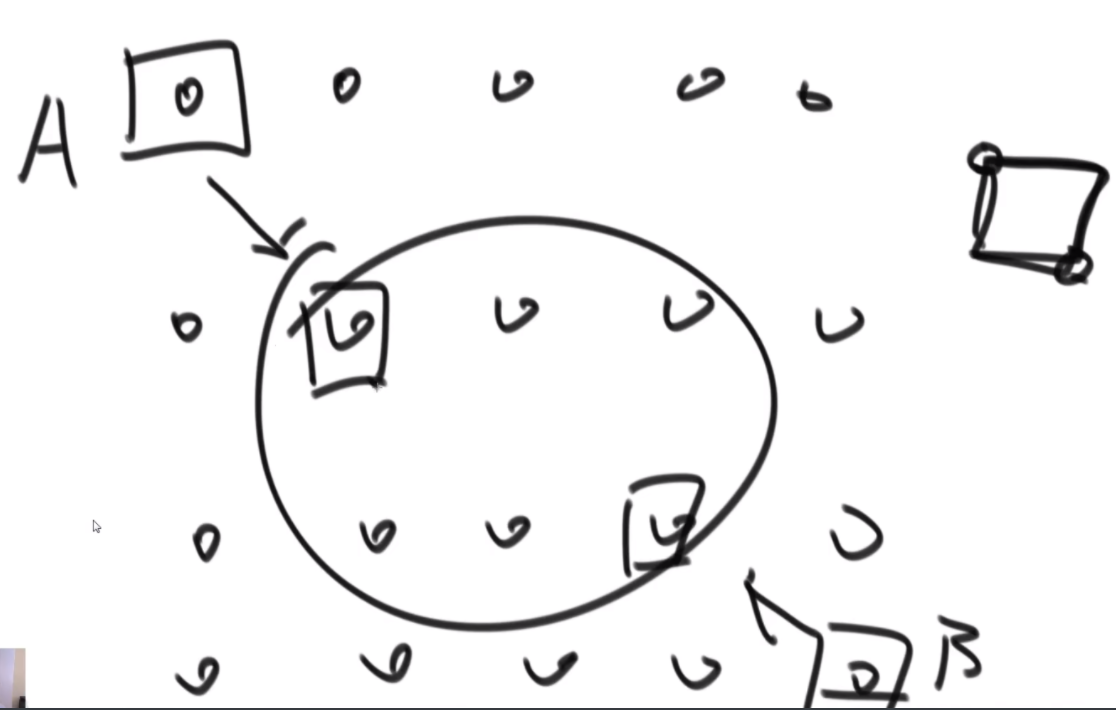

先实现一个函数，给左上角和右下角，然后打印这个方框按照顺序，然后每次循环移动这个左上角和右下角就可以了。A（a,b）B(c,d)，如果ac的时候从左打印到右，bd的时候，从下打印到上，如果都不相等的时候直接打印这个环。

package class03;

public class Problem04_PrintMatrixSpiralOrder {

	public static void spiralOrderPrint(int[][] matrix) {
		int tR = 0;
		int tC = 0;
		int dR = matrix.length - 1;
		int dC = matrix[0].length - 1;
		while (tR <= dR && tC <= dC) {
			printEdge(matrix, tR++, tC++, dR--, dC--);
		}
	}

	public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
		if (tR == dR) {
			for (int i = tC; i <= dC; i++) {
				System.out.print(m[tR][i] + " ");
			}
		} else if (tC == dC) {
			for (int i = tR; i <= dR; i++) {
				System.out.print(m[i][tC] + " ");
			}
		} else {
			int curC = tC;
			int curR = tR;
			while (curC != dC) {
				System.out.print(m[tR][curC] + " ");
				curC++;
			}
			while (curR != dR) {
				System.out.print(m[curR][dC] + " ");
				curR++;
			}
			while (curC != tC) {
				System.out.print(m[dR][curC] + " ");
				curC--;
			}
			while (curR != tR) {
				System.out.print(m[curR][tC] + " ");
				curR--;
			}
		}
	}

	public static void main(String[] args) {
		int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
				{ 13, 14, 15, 16 } };
		spiralOrderPrint(matrix);

	}

}

正方形矩阵每个位置转90度

给定一个正方形矩阵，只用有限几个变量，实现矩阵中每个位置的数顺时针转动

90度，比如如下的矩阵

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

矩阵应该被调整为：

12 8 4 0

13 9 5 1

14 10 6 2

15 11 7 3

思路：和上面一样，先对最外面的那一环进行90度的变换，然后再去搞更里面的一环依次搞。外面这一环，可以分成列数-1组，每组去与对应的地方挨个交换位置。

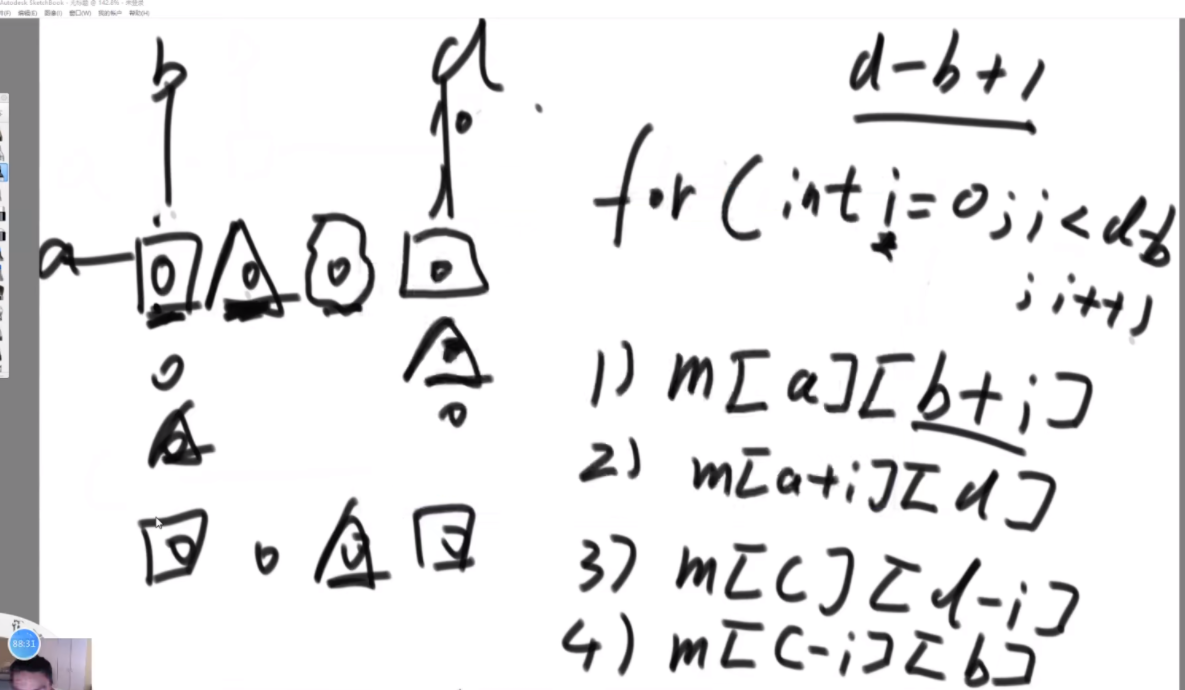
package class03;

public class Problem03_RotateMatrix {

	public static void rotate(int[][] matrix) {
		int tR = 0;
		int tC = 0;
		int dR = matrix.length - 1;
		int dC = matrix[0].length - 1;
		while (tR < dR) {
			rotateEdge(matrix, tR++, tC++, dR--, dC--);
		}
	}

	public static void rotateEdge(int[][] m, int tR, int tC, int dR, int dC) {
		int times = dC - tC; 
		int tmp = 0;
		for (int i = 0; i != times; i++) {
			tmp = m[tR][tC + i];
			m[tR][tC + i] = m[dR - i][tC];
			m[dR - i][tC] = m[dR][dC - i];
			m[dR][dC - i] = m[tR + i][dC];
			m[tR + i][dC] = tmp;
		}
	}

	public static void printMatrix(int[][] matrix) {
		for (int i = 0; i != matrix.length; i++) {
			for (int j = 0; j != matrix[0].length; j++) {
				System.out.print(matrix[i][j] + " ");
			}
			System.out.println();
		}
	}

	public static void main(String[] args) {
		int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
				{ 13, 14, 15, 16 } };
		printMatrix(matrix);
		rotate(matrix);
		System.out.println("=========");
		printMatrix(matrix);

	}

}

拼接字符串到长度n最小步骤数

假设s和m初始化，s = "a"; m = s;

再定义两种操作，第一种操作： m = s; s = s + s; 第二种操作： s = s + m;

求最小的操作步骤数，可以将s拼接到长度等于n

思路：首先有一个策略是，如果n是一个质数，那么第一种操作一定不如第二种操作，第二种操作一定是最好的。

如果不是质数的话，那么一定是几个数相乘的结果，比如21可以是搞7个然后再番3倍或者先搞3个然后再番7倍，至于哪个是更小的总操作数，遍历找最小就好了。因为N不是质数的话，可以用abcd四个质数的相乘表示出来！！！假如是a,b,c,d四个质数，a需要a-1次第二个操作，b需要b-1次第二个操作，因此是a+b+c+d-4。

package class03;

public class Problem06_SplitNbySM {

	// 附加题：怎么判断一个数是不是质数？
	public static boolean isPrim(int n) {
		if (n < 2) {
			return false;
		}
		int max = (int) Math.sqrt((double) n);
		for (int i = 2; i <= max; i++) {
			if (n % i == 0) {
				return false;
			}
		}
		return true;
	}

	// 请保证n不是质数
	// 返回:
	// 0) 所有因子的和，但是因子不包括1
	// 1) 所有因子的个数，但是因子不包括1
	public static int[] divsSumAndCount(int n) {
		int sum = 0;
		int count = 0;
		for (int i = 2; i <= n; i++) {
			while (n % i == 0) {
				sum += i;
				count++;
				n /= i;
			}
		}
		return new int[] { sum, count };
	}

	public static int minOps(int n) {
		if (n < 2) {
			return 0;
		}
		if (isPrim(n)) {
			return n - 1;
		}
		int[] divSumAndCount = divsSumAndCount(n);
		return divSumAndCount[0] - divSumAndCount[1];
	}

}

动态记录出现次数最多的前K个

给定一个字符串类型的数组arr，求其中出现次数最多的前K个。

思路：先搞一个HashMap，遍历整个数组。第一种方法，搞一个大根堆，然后遍历HashMap建立，最后从堆顶拿K个。第二种方法，搞一个Size大小规定为K的小根堆，每次从HashMap里拿的时候直接跟栈顶比较，如果小于栈顶直接不考虑（即，进入小根堆的门槛），大于栈顶则丢掉栈顶，加入这个元素。

假如是想动态的输入字符串（流的思想，需要手动实现堆），需要3个数据结构相互配合：

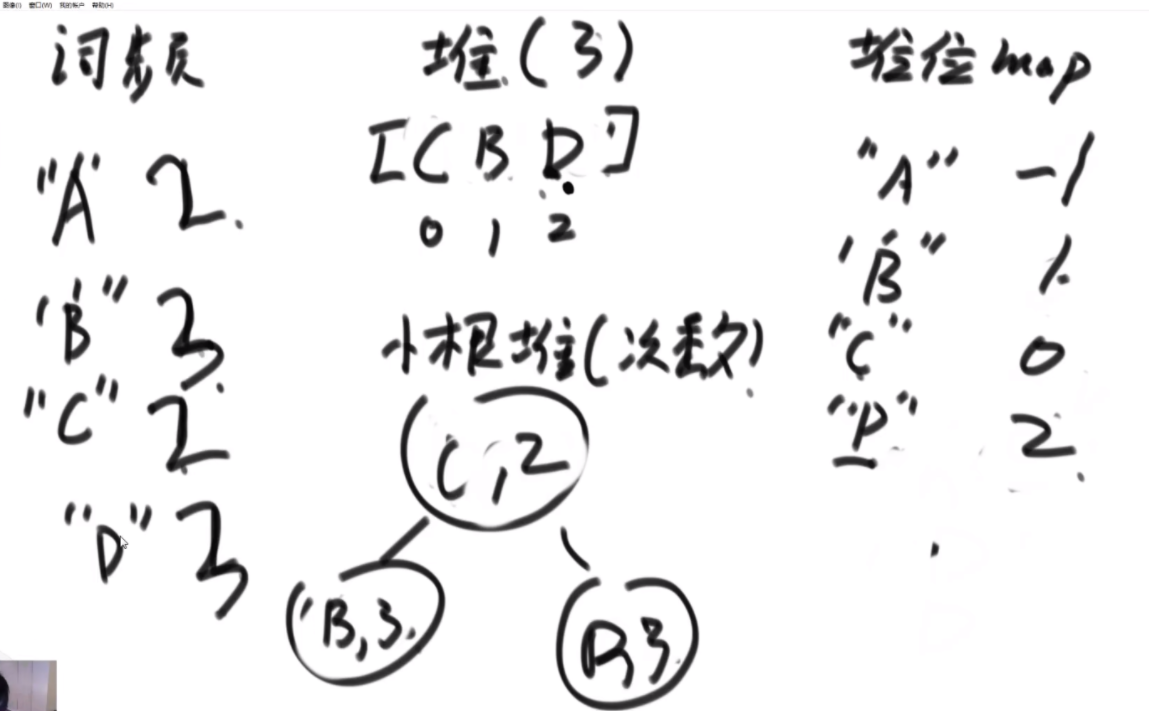
进阶题目的代码：

package ZuoShen2.ZhongClass02;

import java.util.HashMap;

public class TopKTimes {
    public static class Node {
        public String str;
        public int times;

        public Node(String s, int t) {
            str = s;
            times = t;
        }
    }

    public static class TopKRecord{
        //因为Node有自己的词频，因此这个表就是词频表
        private HashMap<String,Node> strNodeMap;
        //堆
        private Node[] heap;
        //如果能在这个表里查到 说明有过记录，如果是-1说明不在堆上，如果>0在堆上
        private HashMap<Node,Integer> nodeIndexMap;
        //堆的大小
        private int heapSize;

        public TopKRecord(int K){
            heap=new Node[K];
            heapSize =0;
            strNodeMap=new HashMap<String,Node>();
            nodeIndexMap=new HashMap<Node,Integer>();
        }

        public void add(String str){
            //当前str对应的节点对象
            Node curNode = null;
            //当前str对应的节点对象是否在堆上
            int preIndex = -1;
            if(!strNodeMap.containsKey(str)){//str第一次出现
                curNode = new Node(str,1);
                strNodeMap.put(str,curNode);
                nodeIndexMap.put(curNode,-1);
            }else {//并非第一次出现
                curNode = strNodeMap.get(str);
                curNode.times++;
                preIndex = nodeIndexMap.get(curNode);
            }
            if(preIndex == -1){//当前str对应的节点对象，词频增加之后，不在堆上
                if(heapSize == heap.length){//考虑能不能干掉最弱的候选人，小根堆的原因
                    if(heap[0].times<curNode.times){
                        nodeIndexMap.put(heap[0],-1);
                        nodeIndexMap.put(curNode,0);
                        heap[0]=curNode;
                        heapify(0, heapSize);
                    }
                }else {
                    nodeIndexMap.put(curNode, heapSize);
                    heap[heapSize]=curNode;
                    heapInsert(heapSize++);
                }
            }else {
                heapify(preIndex, heapSize);
            }
        }

        public void printTopK(){
            System.out.println("TOP:");;
            for (int i = 0; i != heap.length; i++) {
                if(heap[i]==null){
                    break;
                }
                System.out.print("Str:"+heap[i].str);
                System.out.println("Times:"+heap[i].times);
            }
        }

        private void heapInsert(int index){
            while (index!=0){
                int parent = (index)-1/2;
                if(heap[index].times<heap[parent].times){
                    swap(parent,index);
                    index=parent;
                }else {
                    break;
                }
            }
        }

        private void heapify(int index,int heapSize){
            int l = index*2+1;
            int r = index*2+2;
            int smallest = index;
            while (l<heapSize){
                //找到index和它的两个孩子中最小的那个赋给smallest
                if(heap[l].times<heap[index].times){
                    smallest=l;
                }
                if(r<heapSize&&heap[r].times<heap[smallest].times){
                    smallest=r;
                }
                if(smallest!=index){
                    swap(smallest,index);
                }else {
                    break;
                }
                index = smallest;
                l = index*2+1;
                r = index*2+2;
            }
        }

        private void swap(int index1,int index2){
            nodeIndexMap.put(heap[index1],index2);
            nodeIndexMap.put(heap[index2],index1);
            Node temp = heap[index1];
            heap[index1] = heap[index2];
            heap[index2] = temp;
        }


    }
}

p20&p21:

节点能形成多少种不同的二叉树

给定一个非负整数n，代表二叉树的节点个数。返回能形成多少种不同的二叉树结构

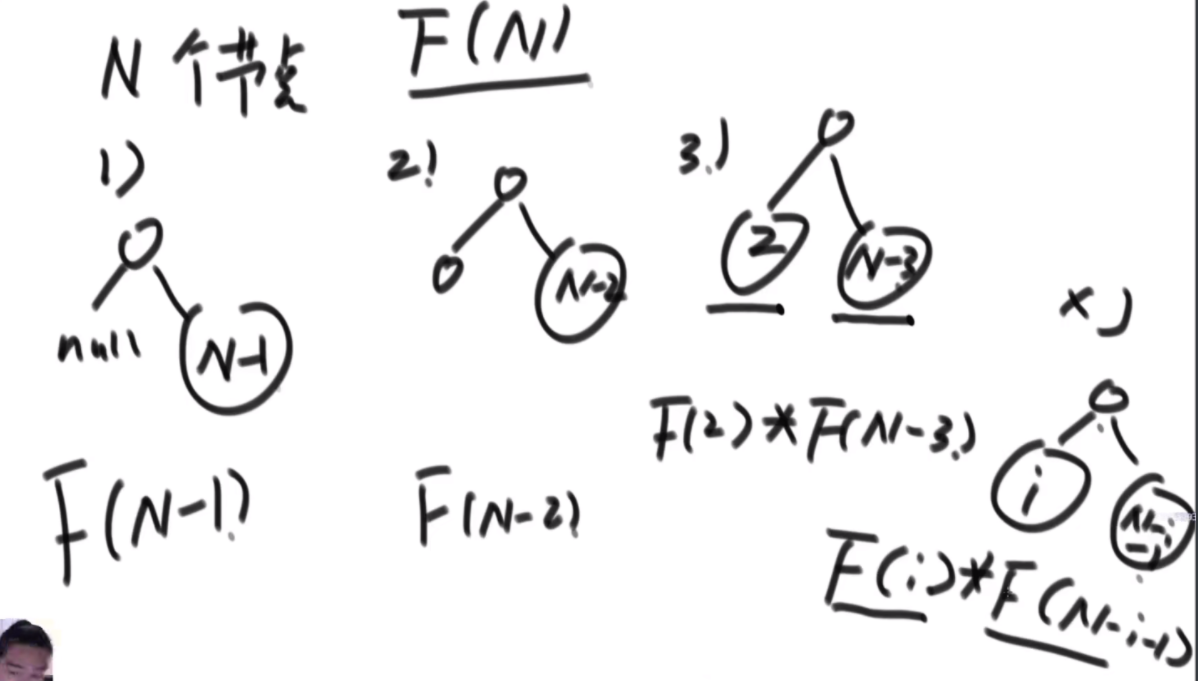
左树有i个节点（i是0-N-1,因为根节点会用去一个节点）,右树是N-i-1个节点，依次递归遍历。总种数为F(i)*F(N-i-1)

 //暴力递归
    public static int process(int n){
        if(n<0){
            return 0;
        }
        if(n<1){
            return 1;
        }
        if(n==2){
            return 1;
        }
        int res=0;
        for (int i = 0; i < n; i++) {
            res=process(i)*process(n-i-1);
        }
        return res;
    }

    //dp做法
    public static int numTrees(int n) {
        if (n < 2) {
            return 1;
        }
        int[] num = new int[n + 1];
        num[0] = 1;
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < i + 1; j++) {
                num[i] += num[j - 1] * num[i - j];
            }
        }
        return num[n];
    }

补全括号

一个完整的括号字符串定义规则如下:

①空字符串是完整的。 ②如果s是完整的字符串，那么(s)也是完整的。③如果s和t是完整的字符串，将它们连接起来形成的st也是完整的。

例如，"(()())", ""和"(())()"是完整的括号字符串，"())(", "()(" 和 ")" 是不完整的括号字符串。

牛牛有一个括号字符串s,现在需要在其中任意位置尽量少地添加括号,将其转化为一个完整的括号字符串。请问牛牛至少需要添加多少个括号。

思路：从左到右依次遍历字符串，如果遇到的是左括号，需要的右括号++，如果遇到的是右括号，需要的左括号--，如果小于0了，那么需要的右括号--。最后把这两种需要的括号加起来。

    public static int needParentheses(String str) {
        int leftRest = 0;  //需要的右括号  （左边多余的左括号）
        int needSolveRight = 0; //需要的左括号   （需要解决的右括号）
        for (int i = 0; i < str.length(); i++) {
            if (str.charAt(i) == '(') {
                leftRest++;
            } else {
                if (leftRest == 0) {
                    needSolveRight++;
                } else {
                    leftRest--;
                }
            }
        }
        return leftRest + needSolveRight;
    }

求差值为k的去重数字对

给定一个数组arr，求差值为k的去重(意味着5，3和3，5是只会保留一个，而且只会出现一次)数字对。

思路：把arr中的所有数加到一个hashmap中，遍历数组，如果看到3，就去找有没有1或5并存起来（后面存数对的时候也要去重判断一下），这个过程时间复杂度O(1)。

平均值移动magic操作

给一个包含n个整数元素的集合a，一个包含m个整数元素的集合b。 定义magic操作为，从一个集合中取出一个元素，放到另一个集合里，且操作过 后每个集合的平均值都大大于于操作前。

注意以下两点：

1）不可以把一个集合的元素取空，这样就没有平均值了

2）值为x的元素从集合b取出放入集合a，但集合a中已经有值为x的元素，则a的 平均值不变（因为集合元素不会重复），b的平均值可能会改变（因为x被取出 了）

问最多可以进行多少次magic操作？

思路：首先分析A,B当两个集合平均值相同的时候，没法动，A平均值大于B的时候，可以将A中大于B平均值且小于A平均值的数拿出来放入B中，全部放入后magic操作就不能继续进行了。这个区间的数，要从小拿到大，这样可以拿的次数最多，原理：拿最小的会让A的平均值提升最大，B的平均值提升最小，这样让两者平均值比较难追上。

这里有个bug，就是两者可能会一直magic。。。

package ZuoShen2.ZhongClass01;

import java.util.Arrays;
import java.util.HashSet;

public class MagicOp {
    // 请保证arr1无重复值、arr2中无重复值，且arr1和arr2肯定有数字
    public static int maxOps(int[] arr1, int[] arr2) {
        double sum1 = 0;
        for (int i = 0; i < arr1.length; i++) {
            sum1 += (double) arr1[i];
        }
        double sum2 = 0;
        for (int i = 0; i < arr2.length; i++) {
            sum2 += (double) arr2[i];
        }
        // 如果平均值一样  那么没法magic
        if (avg(sum1, arr1.length) == avg(sum2, arr2.length)) {
            return 0;
        }
        int[] arrMore = null;
        int[] arrLess = null;
        double sumMore = 0;
        double sumLess = 0;
        if (avg(sum1, arr1.length) > avg(sum2, arr2.length)) {
            arrMore = arr1;
            sumMore = sum1;
            arrLess = arr2;
            sumLess = sum2;
        } else {
            arrMore = arr2;
            sumMore = sum2;
            arrLess = arr1;
            sumLess = sum1;
        }
        Arrays.sort(arrMore);
        HashSet<Integer> setLess = new HashSet<>();
        for (int num : arrLess) {
            setLess.add(num);
        }
        int moreSize = arrMore.length;
        int lessSize = arrLess.length;
        int ops = 0;
        for (int i = 0; i < arrMore.length; i++) {
            double cur = (double) arrMore[i];
            if (cur < avg(sumMore, moreSize) && cur > avg(sumLess, lessSize)
                    && !setLess.contains(arrMore[i])) {
                sumMore -= cur;
                moreSize--;
                sumLess += cur;
                lessSize++;
                setLess.add(arrMore[i]);
                ops++;
            }
        }
        return ops;
    }

    public static double avg(double sum, int size) {
        return sum / (double) (size);
    }

    public static void main(String[] args) {
        int[] arr1 = { 1, 2, 5 };
        int[] arr2 = { 2, 3, 4, 5, 6 };
        System.out.println(maxOps(arr1, arr2));

    }
}

计算括号深度

一个合法的括号匹配序列有以下定义:

①空串""是一个合法的括号匹配序列 ②如果"X"和"Y"都是合法的括号匹配序列,"XY"也是一个合法的括号匹配序列 ③如果"X"是一个合法的括号匹配序列,那么"(X)"也是一个合法的括号匹配序列 ④每个合法的括号序列都可以由以上规则生成。

例如: "","()","()()","((()))"都是合法的括号序列

对于一个合法的括号序列我们又有以下定义它的深度: ①空串""的深度是0 ②如果字符串"X"的深度是x,字符串"Y"的深度是y,那么字符串"XY"的深度为 max(x,y) 3、如果"X"的深度是x,那么字符串"(X)"的深度是x+1

例如: "()()()"的深度是1,"((()))"的深度是3。

牛牛现在给你一个合法的括号序列,需要你计算出其深度。

思路：定义一个count，遇到左括号++，右括号--，遍历从头到尾，countd达到的最大值，就是深度。

public static boolean isValid(char[] str) {
    if (str == null || str.equals("")) {
        return false;
    }
    int status = 0;
    for (int i = 0; i < str.length; i++) {
        if (str[i] != ')' && str[i] != '(') {
            return false;
        }
        if (str[i] == ')' && --status < 0) {
            return false;
        }
        if (str[i] == '(') {
            status++;
        }
    }
    return status == 0;
}
public static int deep(String s) {
		char[] str = s.toCharArray();
		if (!isValid(str)) {
			return 0;
		}
		int count = 0;
		int max = 0;
		for (int i = 0; i < str.length; i++) {
			if (str[i] == '(') {
				max = Math.max(max, ++count);
			} else {
				count--;
			}
		}
		return max;
	}

括号子串的最大长度

思路:搞一个数组，这个数组记录，以i位置结束的最长的子串的长度。如果以'('结尾则直接GG，因为一定不合法，如果是'）'那么看它前一个位置的是不是('，那么+2，并且继续往前走（代表加上arr[pre-1]，如果pre-1不越界的话），这里至于要+一次，因为pre-1位置上已经加过之前的，不需要重复加。

public static int maxLength(String str) {
		if (str == null || str.equals("")) {
			return 0;
		}
		char[] chas = str.toCharArray();
		int[] dp = new int[chas.length];
		int pre = 0;
		int res = 0;
		for (int i = 1; i < chas.length; i++) {
			if (chas[i] == ')') {
				pre = i - dp[i - 1] - 1;//右括号说明前面可能有子串，那么看前面的最大子串的前一个字符是啥
				if (pre >= 0 && chas[pre] == '(') {
					dp[i] = dp[i - 1] + 2 + (pre > 0 ? dp[pre - 1] : 0);
				}
			}
			res = Math.max(res, dp[i]);
		}
		return res;
	}

用一个栈排序

请编写一个程序，对一个栈里的整型数据，按升序进行排序（即排序前，栈里的数据是无序的，排序后最大元素位于栈顶），要求最多只能使用一个额外的栈存放临时数据，但不得将元素复制到别的数据结构中。

思路：就搞一个临时栈，维持它的元素顺序是从栈顶到栈底由小到大，每次取出原始栈栈顶放入临时栈，如果这个元素小于临时栈栈顶，直接压入，如果大于，那么弹出临时栈栈顶放入原始栈直到可以放入这个元素，放入后继续。

p19:

绳子最多能覆盖几个点

给定一个有序数组arr，代表数轴上从左到右有n个点arr[0]、arr[1]...arr[n－1]， 给定一个正数L，代表一根长度为L的绳子，求绳子最多能覆盖其中的几个点。

普通思路：贪心策略：其中绳子的右侧端点放在某个点上，看绳子主体覆盖了几个点，枚举所有点找到最多的那个。其中可以判断大于等于绳子左侧端点最左侧的值（脚标）是谁（可以使用二分查找），然后右端点减去这个值（脚标）再加一就是个数。时间复杂度O(nlogn)。

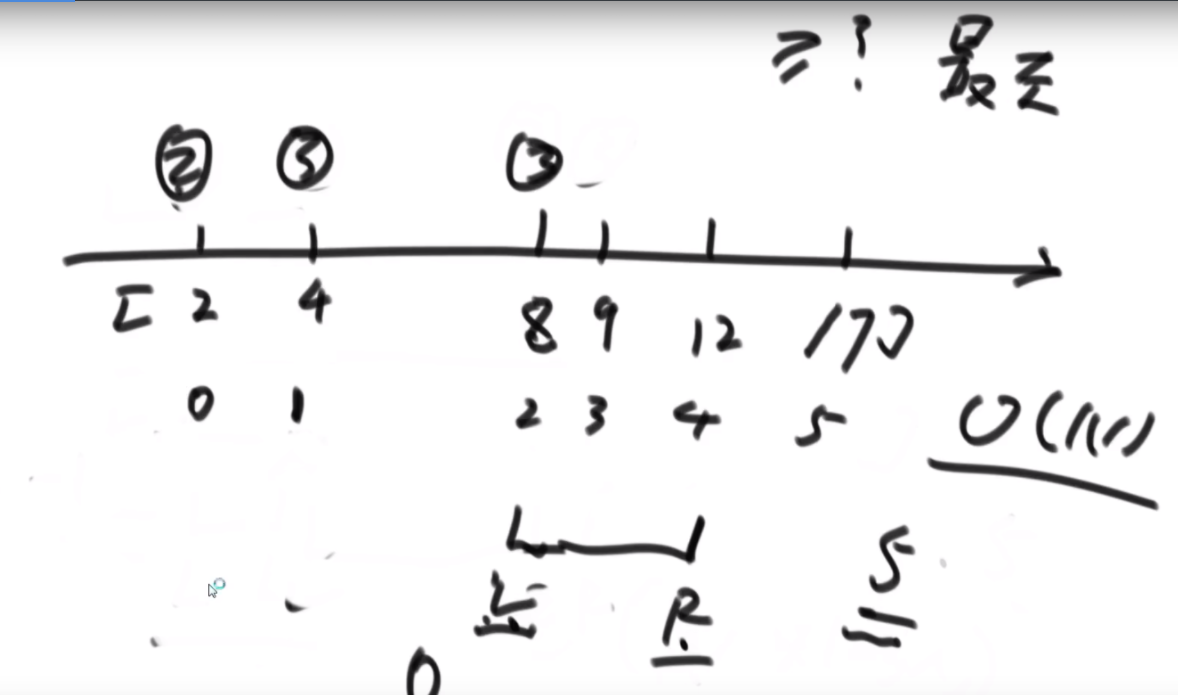
滑动窗口思路:有L和R指针，L先从第一个点开始，然后R开始尝试能不能往右走，走不了的时候就停，记录个数到开头位置。然后L来到开头节点的下一个点，继续让R往后走，走不了的时候就停，记录个数到开头位置。以此往复。

package ZuoShen2.ZhongClass01;

public class CordCoverMaxPoint {
    //第一种思路 N*LogN的复杂度
    public static int maxPoint(int[] arr, int L) {
        //arr代表的是那些点  L代表绳子长度
        int res = 1;
        for (int i = 0; i < arr.length; i++) { //遍历点
            //这里相当于是绳子的右端放在一个点上 然后绳子左端往左伸
            //找到能伸到的最左侧的节点 即在arr[0..i]范围上，找满足>=value的最左位置
            int nearest = nearestIndex(arr, i, arr[i] - L);
            res = Math.max(res, i - nearest + 1);
        }
        return res;
    }

    // 在arr[0..R]范围上，找满足>=value的最左位置
    // 二分查找  如果满足>=value就R往左走 不满足L就往左走
    public static int nearestIndex(int[] arr, int R, int value) {
        int L = 0;
        int index = R;
        while (L < R) {
            int mid = L + ((R - L) >> 1);
            if (arr[mid] >= value) {
                index = mid;
                R = mid - 1;
            } else {
                L = mid + 1;
            }
        }
        return index;
    }

    //第二种思路 N的复杂度(手撸的)
    public static int maxPoint2(int[] arr, int length) {
        //arr代表的是那些点  L代表绳子长度
        int res = 1;
        int l=0,r=0;
        for (int i = 0; i < arr.length-1; i++) {
            l=i;
            r=i+1;
            while (r<arr.length){ //防止越界
                if(arr[r]-arr[l]<=length){
                    r++;  //因为r每次都会多加一次  因此最后是r-l
                }else {
                    break;
                }
            }
            res=Math.max(res,r-l);
        }
        return res;
    }



    public static void main(String[] args) {
        int[] arr = { 0, 13, 24, 35, 46, 57, 65, 69, 70 };
        int L = 6;

        System.out.println(maxPoint(arr, L));
        System.out.println(maxPoint2(arr, L));

    }
}

最少使用的袋子

小虎去附近的商店买苹果，奸诈的商贩使用了捆绑交易，只提供6个每袋和8个每袋的包装包装不可拆分。可是小虎现在只想购买恰好n个苹果，小虎想购买尽量少的袋数方便携带。如果不能购买恰好n个苹果，小虎将不会购买。输入一个整数n，表示小虎想购买的个苹果，返回最小使用多少袋子。如果无论如何都不能正好装下，返回-1。

首先简单的分析一下，奇数的个数是一定不能装的。

普通思路：先试试尽量用8类型的袋子装，剩下的用6类型的袋子装，发现装不了，那么减少一个8类型的袋子，再试，直到试出一个方案，或者8类型的袋子一个都用不了（8类型的0个）还是不行，那么返回-1。（贪心策略）

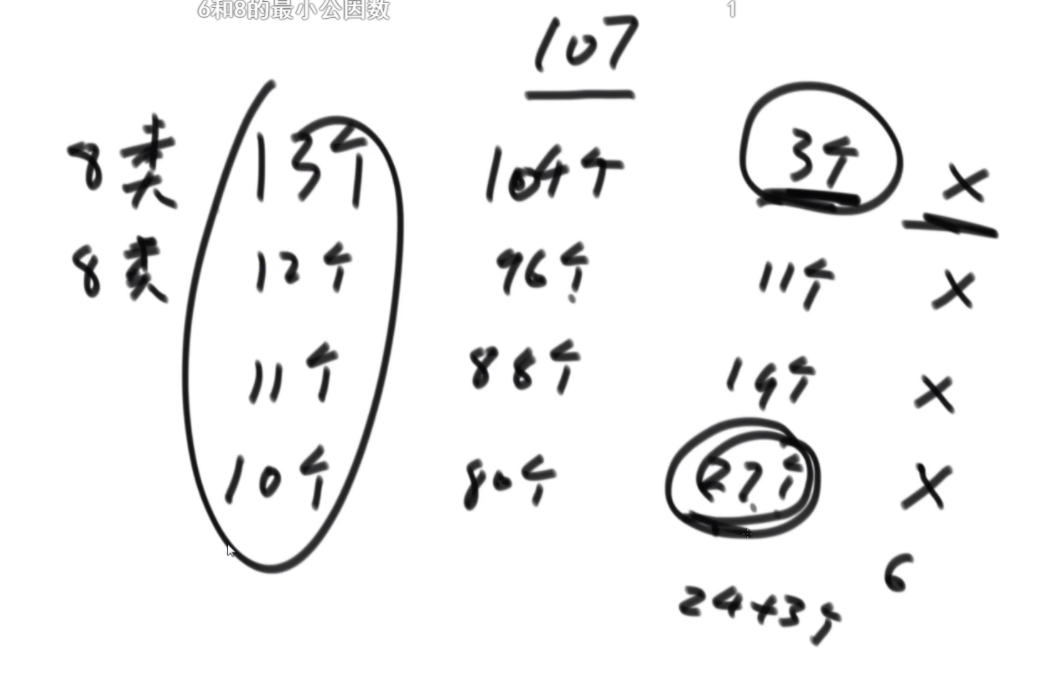
这个普通思路可以优化一下，剩余苹果数大于24就不用试了。（24是6和8的最小公倍数）原因一：同样是24个，为什么不用8类型而用6类型的装？因此这个有问题。原因二：就是在剩余个数超过24的时候，可以直接不用试了，因为想解决27个的时候一定是先解决掉24个，剩下的3个之前已经试过了，那么一定是解决不了的。

打表法思路：如果是输入一个整型，输出一个整型。直接实现一个傻白甜思路，然后搞一个对数器，从1输出到10000，然后找规律，然后根据这个规律硬捏出代码，直接是最优解。。。至于数学规律直接不关心。

吃草四次幂先后手问题

最初有一个装有n份青草的箱子,先手和后手依次进行,先手先开始。在每个回合中,每个玩家必须吃一些箱子中的青草,所吃的青草份数必须是4的x次幂,比如1,4,16,64等等。不能在箱子中吃到有效份数青草的玩家落败。假定先手和后手都是按照最佳方法进行游戏,请输出胜利者的名字。

普通思路：递归，小于5的人为规定出来，然后其他的交给子过程去试一试，一直试到n都不能赢的话就G，一次赢了就是赢了。

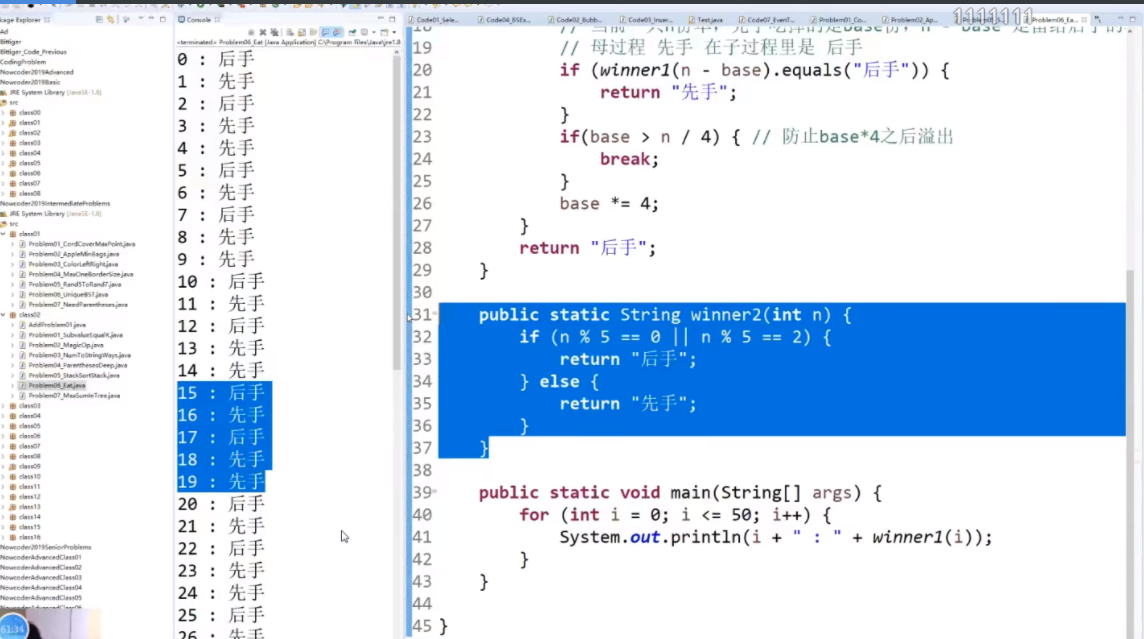
打表法思路：对数器用普通思路的方法输出值，找规律上图中可以看到，规律就是“后先后先先”，因此直接出结果。

package ZuoShen2.ZhongClass01;

public class Eat {
    //n份青草放在一堆
    //先手后手都绝顶聪明
    // string "先手""后手"
    public static String winner1(int n){
        // 0  1 2  3  4
        // 后 先 后 先 先
        if(n<5){
            return (n==0||n==2)?"先手":"后手";
        }
        //n>=5时
        int base = 1; //先手决定吃的草
        //有问题
        while (base<=n){
            // 当前一共n份艹，先手吃掉的base份，n-base是留给后手的艹
            // 母过程 先手 在子过程里是后手
            if(winner1(n-base).equals("后手")){
                return "先手";
            }
            if(base>n/4){ //防止*4后溢出 如果base*4后大于n 那么一定不可能赢 因此直接break
                break;
            }
            base*=4;
        }
        return "后手";
    }
    //对数器思路
    public static void printWinner(int n) {
        if (n % 5 == 0 || n % 5 == 2) {
            System.out.println("yang");
        } else {
            System.out.println("niu");
        }
    }
}

染色正方体让R比G在更左侧

牛牛有一些排成一行的正方形。每个正方形已经被染成红色或者绿色。牛牛现在可以选择任意一个正方形然后用这两种颜色的任意一种进行染色,这个正方形的颜色将会被覆盖。牛牛的目标是在完成染色之后,每个红色R都比每个绿色G距离最左侧近。牛牛想知道他最少需要涂染几个正方形。

如样例所示: s = RGRGR我们涂染之后变成RRRGG满足要求了,涂染的个数为2,没有比这个更好的涂染方案。

普通思路：遍历整个数组，先是左边第一个是R 右边全是G，然后左边第二个是R 右边全是G，以此类推，最后比较这些方案中需要染色最少的，得到答案。时间复杂度O(N²)

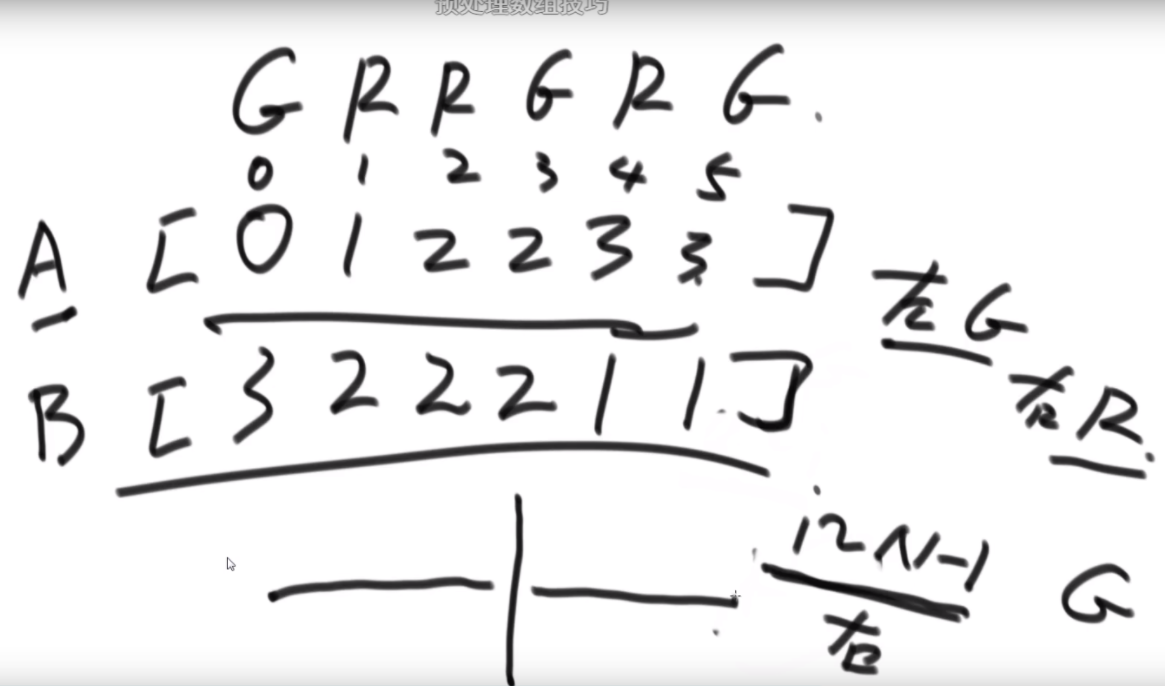
预处理思路：申请两个数组，A去保存从0-i的所有R的个数，比如脚标是0的就是0-0 0个R，脚标是4的就是0-4 3个R。B去保存i-N-1的G的个数，方法类似上面。这样可以优化，每次遍历的时候就不用重新走一遍计算个数了，直接查数组就可以了，因此时间复杂度是O(N)。

package ZuoShen2.ZhongClass01;

public class ColorLeftRight {
    //普通思路  很简单  不写了 时间复杂度O(N平方)

    // RGRGR -> RRRGG
    public static int minPaint(String s) {
        if (s == null || s.length() < 2) {
            return 0;
        }
        char[] chs = s.toCharArray();
        int[] right = new int[chs.length];
        right[chs.length - 1] = chs[chs.length - 1] == 'R' ? 1 : 0;
        for (int i = chs.length - 2; i >= 0; i--) {
            right[i] = right[i + 1] + (chs[i] == 'R' ? 1 : 0);
        }
        int res = right[0];
        int left = 0;
        for (int i = 0; i < chs.length - 1; i++) {
            left += chs[i] == 'G' ? 1 : 0;
            res = Math.min(res, left + right[i + 1]);
        }
        res = Math.min(res, left + (chs[chs.length - 1] == 'G' ? 1 : 0));
        return res;
    }

    public static void main(String[] args) {
        String test = "GGGGGR";
        System.out.println(minPaint(test));

    }
}

边框全是1的最大正方形的边

给定一个N*N的矩阵matrix，只有0和1两种值，返回边框全是1的最大正方形的边长长度。

例如:

01111

01001

01001

01111

01011

其中边框全是1的最大正方形的大小为4*4，所以返回4。

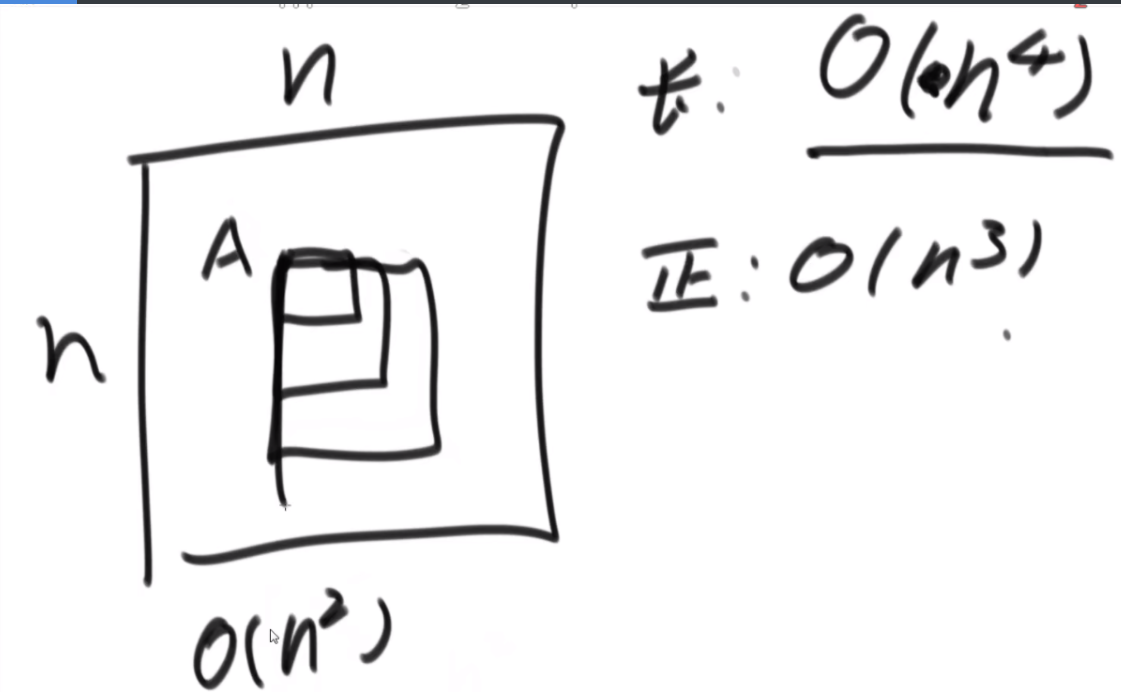
预备知识：给一个n*n大小的正方形，那么里面长方形个数O(n⁴)，原因是选择一个点O(n²)，再选择一个点O(n²)，这两个点就可以构成一个唯一的矩阵，虽然是有重复的，但是常数项会低，个数程度还是O(n⁴)。正方形个数O(n³)，原因是选择一个点O(n²)，然后以这个点为左上角，边长为1，为2，为3，一直到最大限度，这个过程是O(n)的，因此总的为O(n³)。

普通思路：O(n³)个正方形，每个需要验证4条边都为1，因此需要4*O(n)个判断，总时间复杂度就是O(n⁴)

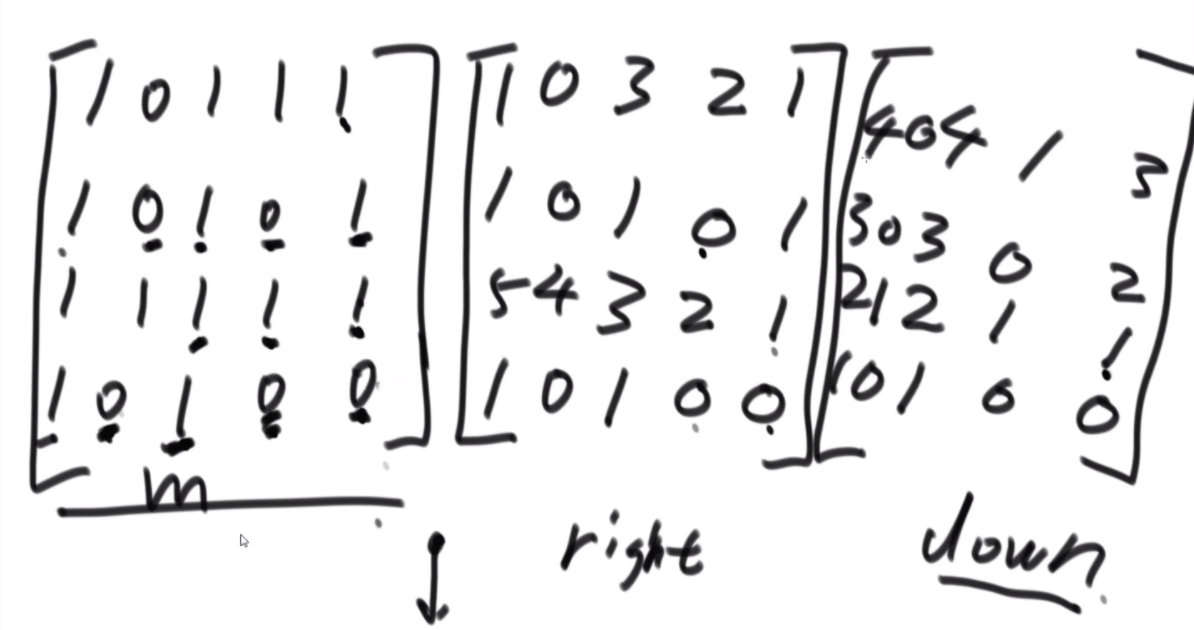
预处理思路：O(n³)个正方形，构建两个数组，right数组记录每个点，算上自己向右连续的1一共有多少个。down数组记录每个点，算上自己向下连续的1一共有多少个。然后有了这些数据后，在O(n³)个正方形基础上，只需要O(1)的时间就能判断是不是全为1的正方形。达到优化。

等概率返回函数问题

给定一个函数f，可以1～5的数字等概率返回一个。请加工出1～7的数字等概率返回一个的函数g。

给定一个函数f，可以a～b的数字等概率返回一个。请加工出c～d的数字等概率返回一个的函数g。

思路：上面这两类问题都可以用一种解决，先把f函数加工成01等概率函数发生器，然后用这个发生器去等概率表示g函数。f函数的处理：1～5中，让1～2定义为0，2～4定义为1，如果是5的话重新来，那么就获得了等概率发生器，a～b的数字也是，对半分，多出来的一个数字重新走循环。g函数的处理：13～20的话，改成0～7，然后加上13，去搞一个0～7的生成器。这个可以用三位二进制数表示，因此可以随机生成3个二进制数，第一个数左移两位，第二个数左移一位，第三个数不动，三个数加起来，如果是大于7的直接重新进循环。

给定一个函数f，以p概率返回0，以1-p概率返回1。请加工出等概率返回0和1的函数g。

思路：定义两个二进制位，让f函数一直生成，如果是00或者11的组合就重新进循环，如果是01定义为0，如果是10定义为1，因此生成了g函数。利用的是概率：01概率是px(1-p) 10概率是(1-p)xp 因此是等概率。

p18:

有序表的讲解

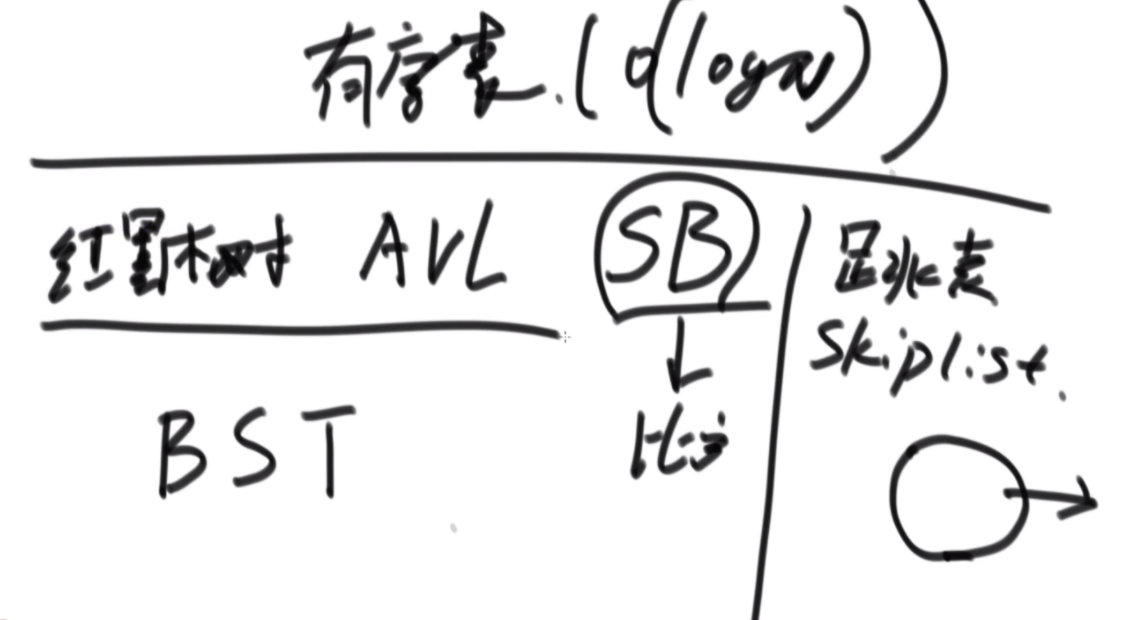
有序表时间复杂度都是O(logN)级别的。分为这四种，其中最常用的（比赛里）是SizeBalance树，俗称SB树。这四种可以分为两大类，第一个大类是红黑树、AVL树和SB树，因为它们都是平衡搜索二叉树BST系列，而跳表SkipList是用单链表实现的。

搜索二叉树的增删查：

• 增加：从头结点开始滑，比当前节点小就往左滑，比当前节点大就往右滑，直到找到相等的节点，添加到这个链表里或者走到空，直接放在那里。
• 查找：头结点是4的话，查找≤6的，那么直接头结点以及左子树都是，然后再从右子树开始滑。
• 删除：先搜索到这个节点，如果左右孩子都没有直接删，如果左右孩子不全，直接让其中一个孩子替代它。如果左右孩子都全，可以用左子树最右的节点或者用右子树最左的节点替代。

但是因为没有平衡性，因此时间复杂度取决于数据状况，因此要弄成平衡搜索二叉树。（现在容易斜）通过有左旋和右旋操作，以及对自身平衡性的定义实现。AVL树要求每个节点左右子树高度差不能超过1。

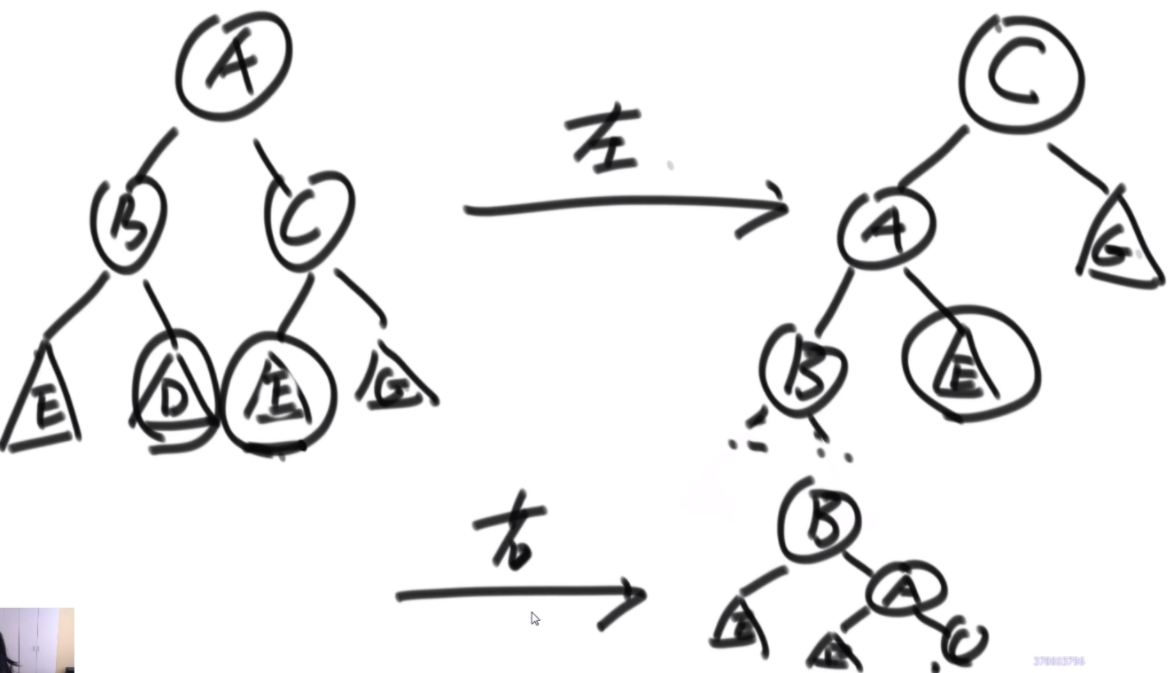
左旋：头结点往左边倒，右旋：头结点往右边倒。

AVL树

，在加入一个节点后，会从这个节点出发往上，所有节点都看一下有没有平衡性。删除的时候也是，不过删除的第三种情况左右孩子都全的时候，从那个节点去替它的上一个节点去往上检查。

LL：左树的左孩子过长，做一次右旋。RR：右树的右孩子过长，做一次左旋。

LR：左孩子的右孩子导致的，就让这个节点的父节点先左旋，然后再让新的父节点右旋，让这个节点到达最头部，完成调整。RL：右孩子的左孩子导致的，就让这个节点的父节点先右旋，然后再让新的父节点左旋，让这个节点到达最头部，完成调整。

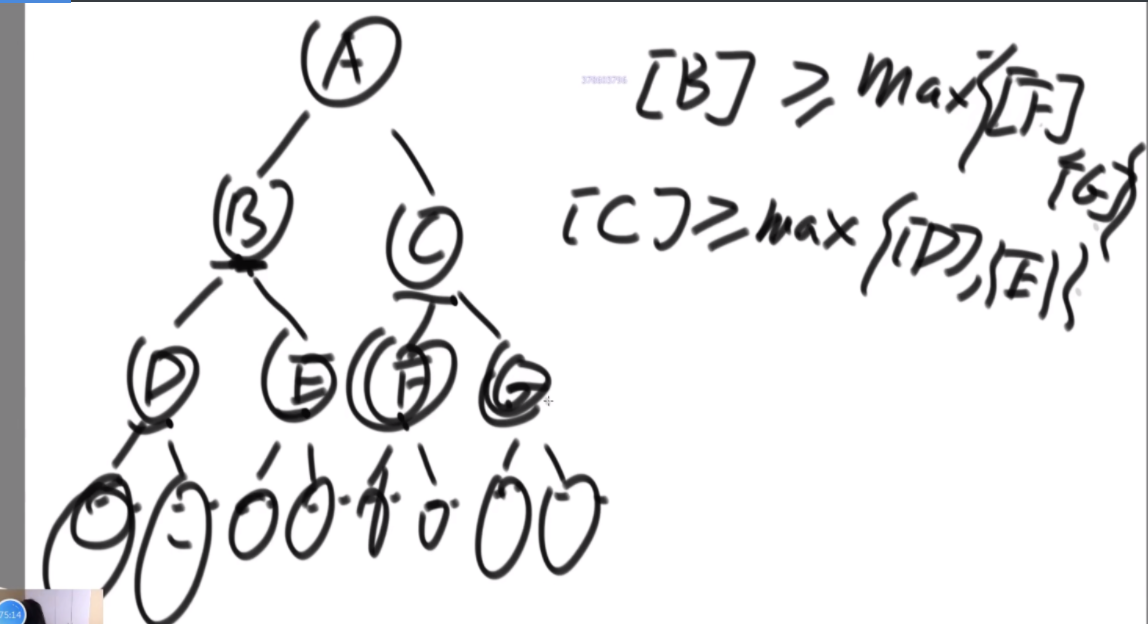
SizeBalanceTree

任何一个节点大小（这个节点作为根节点，这棵树的总节点个数），大于自己的侄子节点。

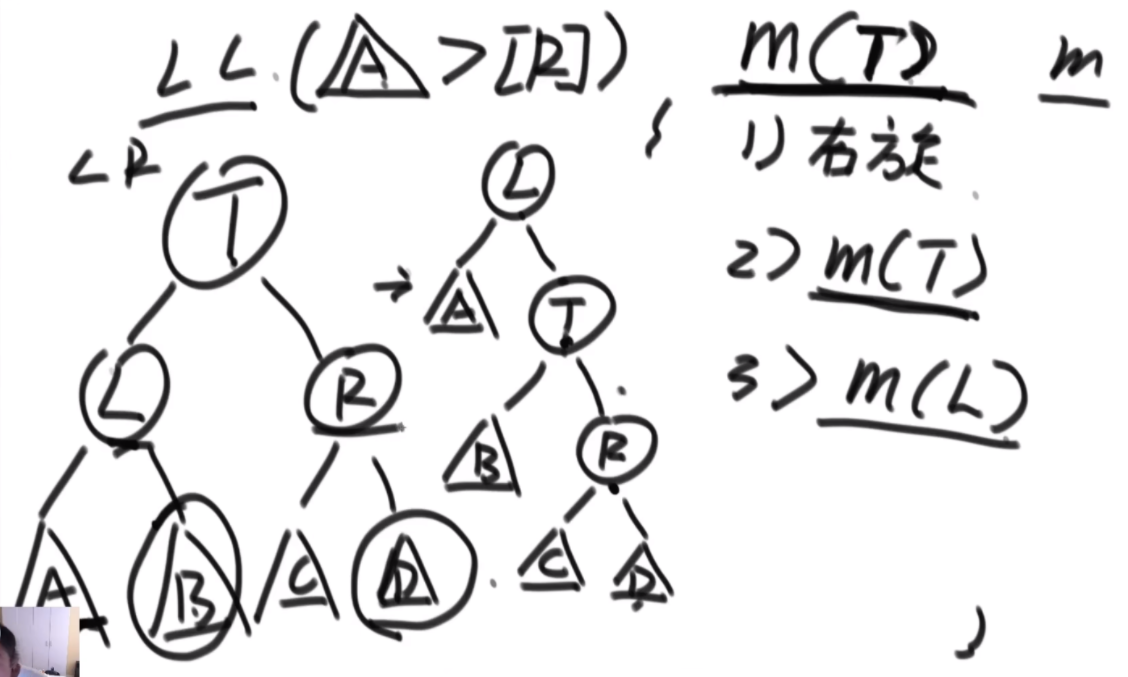
LL如上：A的节点数大于R的节点数，因此T第一步先右旋，第二步再次对T进行平衡性检查，因为T的子节点动了，第三部检查L，因为T作为L的子节点动了。这个检查是自下向上的。RR差不多，就是D>L。

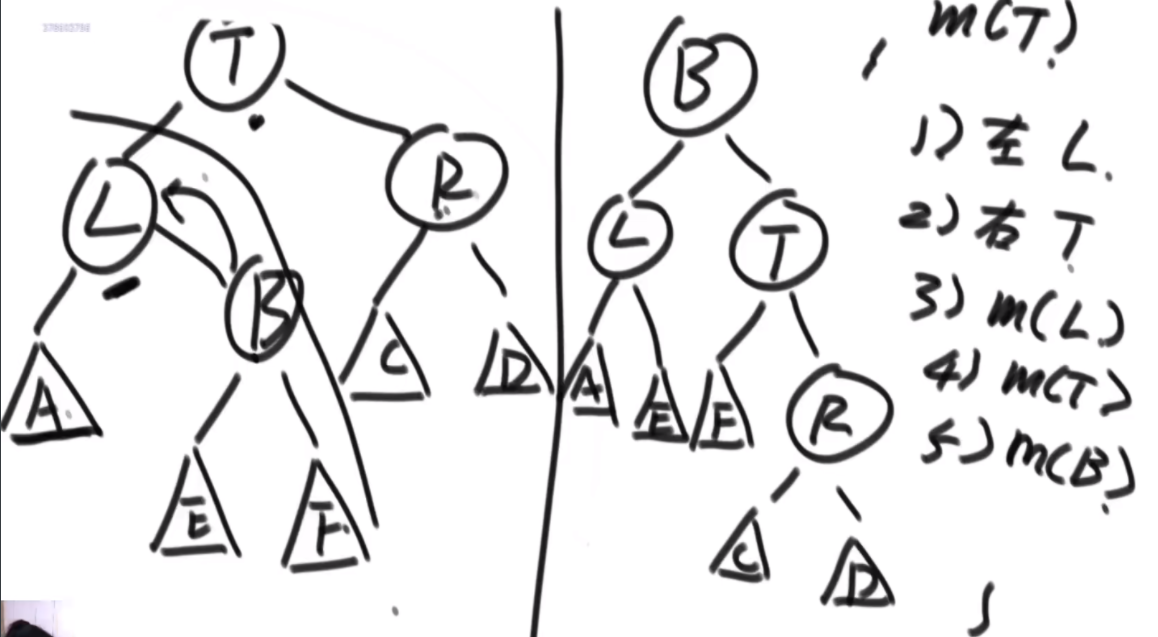
LR：对T的操作简写为m(T)，因此第一步左旋L第二步右旋T第三部m(L)第四步m(T)第五步m(B) RL一样。

红黑树

1. 节点是红色或者黑色
2. 根节点是黑色
3. 每个叶子的节点都是黑色的空节点（NULL）
4. 每个红色节点到两个子节点都是黑色的
5. 从任意节点到其每个叶子的所有路径都包含相同数目的黑色节点。

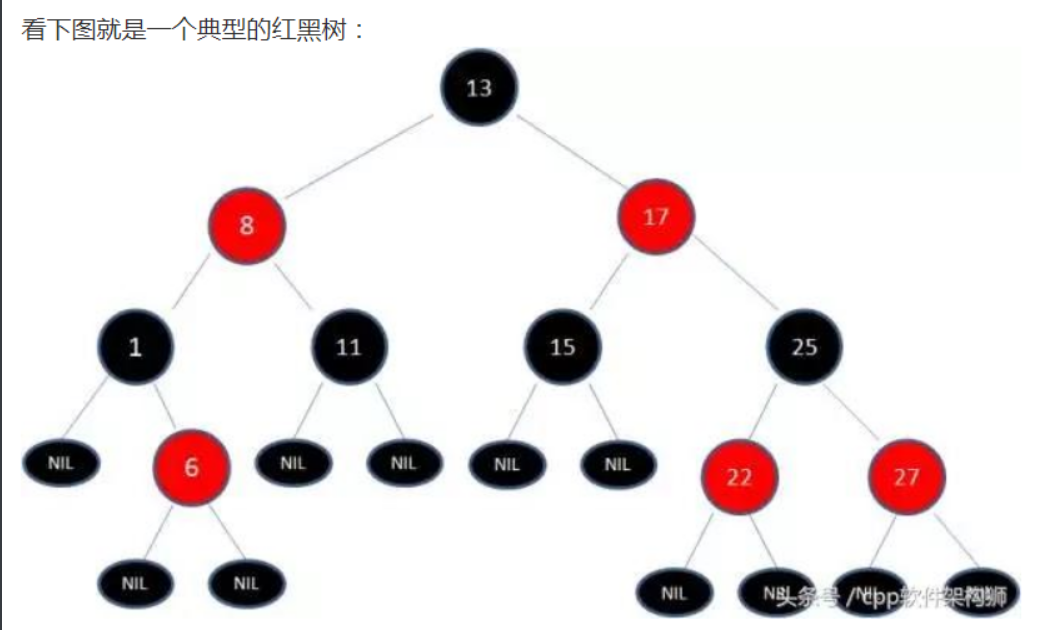
跳表

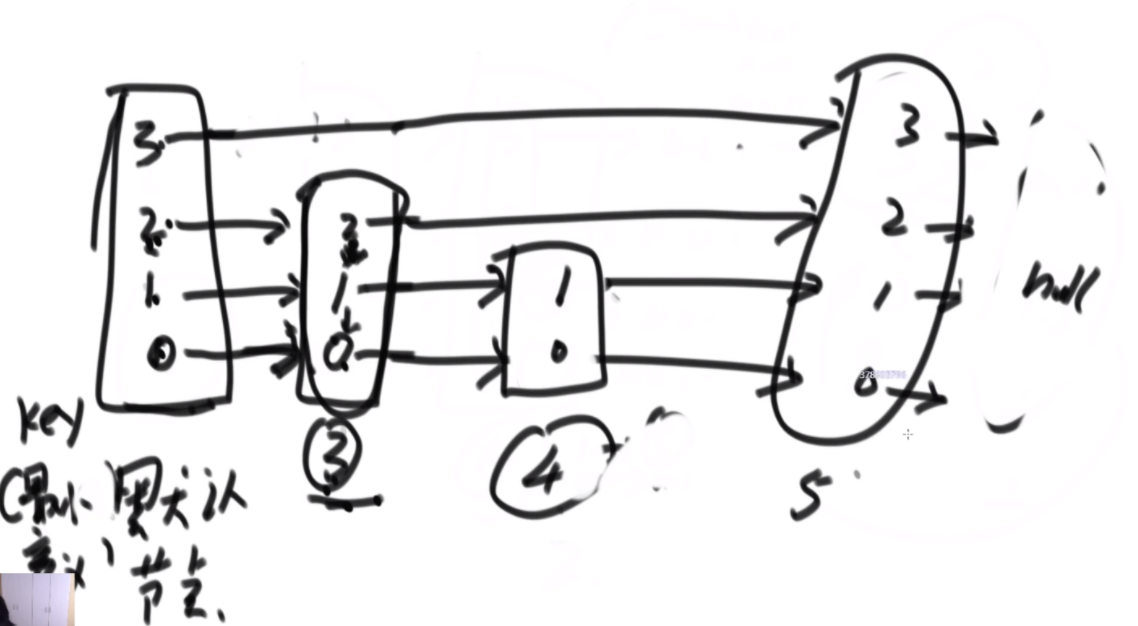
跳表首先是一个初始的默认节点，这个默认节点大小是无限小，每个节点都有层数，默认节点的层数会和最高节点的层数是一样的。

添加：每一个新进来的节点 会掷骰子，随机一个层数，然后放到比它大的第一个节点的左边，然后连接左右两侧的链表，假设插入70这个节点（第二张图），首先在最高的地方找第一个小于70 的，是20这个节点，但是70是两层的，因此往下走走到20节点的第四层，这一层中比70小的第一个节点是50，然后从50一直走到第二层，开始添加70节点。

查找：跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。首先在最高级索引上查找最后一个小于当前查找元素的位置，然后再跳到次高级索引继续查找，直到跳到最底层为止，这时候以及十分接近要查找的元素的位置了(如果查找元素存在的话)。由于根据索引可以一次跳过多个元素，所以跳查找的查找速度也就变快了。

p17:

聪明绝顶的玩家见P10

象棋中马的跳法

【题目】 请同学们自行搜索或者想象一个象棋的棋盘，然后把整个棋盘放入第一象限，棋盘的最左下 角是(0,0)位置。那么整个棋盘就是横坐标上9条线、纵坐标上10条线的一个区域。给你三个 参数，x，y，k，返回如果“马”从(0,0)位置出发，必须走k步，最后落在(x,y)上的方法数 有多少种？

很像机器人的那个，不过是三维的。

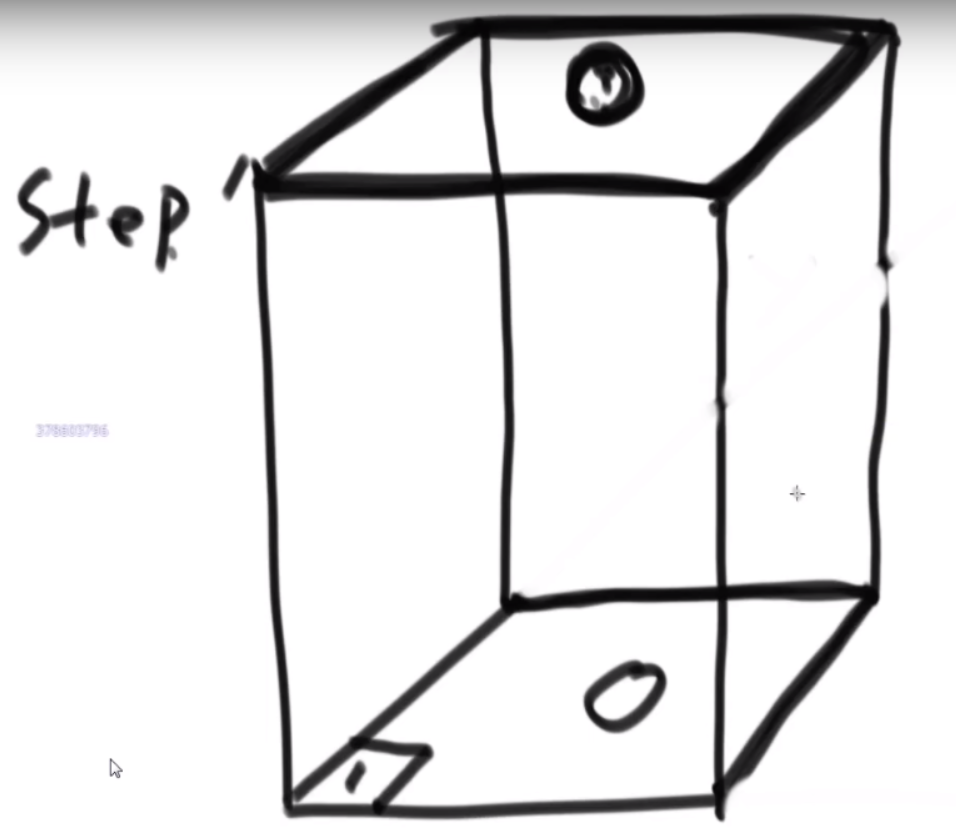
这里step每一步都可以看成一个面，这个面由x,y组成，step=0的时候，只有x0&&y0这个点为1，其余全为0，step=1的面由下面的一个面决定，因此可以一直往上推。

package ZuoShen2.Class05;

public class HorseJump {
    public static int getWays(int x, int y, int step) {
        return process(x, y, step);
    }

    // 潜台词：从（0，0）位置出发
    // 要去往(x,y)位置 但是必须要跳step步
    // 返回方法数
    //不过这个函数可以理解为从x,y跳到了0，0 结果是一样的
    public static int process(int x, int y, int step) {
        if (x < 0 || x > 8 || y < 0 || y > 9) {
            return 0;//这里0就代表了无法到达，因此不需要-1去搞无效解
        }
        if (step == 0) {
            return (x == 0 && y == 0) ? 1 : 0;
        }
        return process(x - 1, y + 2, step - 1)
                + process(x + 1, y + 2, step - 1)
                + process(x + 2, y + 1, step - 1)
                + process(x + 2, y - 1, step - 1)
                + process(x + 1, y - 2, step - 1)
                + process(x - 1, y - 2, step - 1)
                + process(x - 2, y - 1, step - 1)
                + process(x - 2, y + 1, step - 1);
    }

    public static int dpWays(int x, int y, int step) {
        if (x < 0 || x > 8 || y < 0 || y > 9 || step < 0) {
            return 0;
        }
        //step+1为高度
        int[][][] dp = new int[9][10][step + 1];
        //第0层的面 只有(0,0)位置是1
        dp[0][0][0] = 1;
        for (int h = 1; h <= step; h++) {//层

            for (int r = 0; r < 9; r++) {
                for (int c = 0; c < 10; c++) {
                    //根据下面的一层决定这一层
                    dp[r][c][h] += getValue(dp, r - 1, c + 2, h - 1);
                    dp[r][c][h] += getValue(dp, r + 1, c + 2, h - 1);
                    dp[r][c][h] += getValue(dp, r + 2, c + 1, h - 1);
                    dp[r][c][h] += getValue(dp, r + 2, c - 1, h - 1);
                    dp[r][c][h] += getValue(dp, r + 1, c - 2, h - 1);
                    dp[r][c][h] += getValue(dp, r - 1, c - 2, h - 1);
                    dp[r][c][h] += getValue(dp, r - 2, c - 1, h - 1);
                    dp[r][c][h] += getValue(dp, r - 2, c + 1, h - 1);
                }
            }
        }
        return dp[x][y][step];
    }

    public static int getValue(int[][][] dp, int row, int col, int step) {
        if (row < 0 || row > 8 || col < 0 || col > 9) {
            return 0;
        }
        return dp[row][col][step];
    }

    public static void main(String[] args) {
        int x = 7;
        int y = 7;
        int step = 10;
        System.out.println(getWays(x, y, step));
        System.out.println(dpWays(x, y, step));
    }
}

Bob的生存概率

【题目】

给定五个参数n,m,i,j,k。表示在一个N*M的区域，Bob处在(i,j)点，每次Bob等概率的向上、 下、左、右四个方向移动一步，Bob必须走K步。如果走完之后，Bob还停留在这个区域上， 就算Bob存活，否则就算Bob死亡。请求解Bob的生存概率，返回字符串表示分数的方式。

不考虑死，那么K步，一共走的可能数为4^K个 再求出活着的数量，然后除一下就是概率（因为是分数表达，因此需要求一下最大公约数，然后两个值同时除以最大公约数获得分数形式）。改为动态规划的话和马一样，同款3维。

package ZuoShen2.Class05;

public class BobDie {
    public static String bob1(int N, int M, int i, int j, int K) {
        long all = (long) Math.pow(4, K);
        long live = process(N, M, i, j, K);
        long gcd = gcd(all, live);
        return String.valueOf((live / gcd) + "/" + (all / gcd));
    }

    // N*M的区域，Bob从(row,col)位置出发，走rest步后，获得生存的方法数
    public static long process(int N, int M, int row, int col, int rest) {
        if (row < 0 || row == N || col < 0 || col == M) { //越界
            return 0;
        }
        if (rest == 0) { //没越界 而且不用走了
            return 1;
        }
        //还没走完 也没越界  往上下左右走都是不同的方法 所以累加  类似于马的八种跳法
         long live = process(N, M, row - 1, col, rest - 1);
        live += process(N, M, row + 1, col, rest - 1);
        live += process(N, M, row, col - 1, rest - 1);
        live += process(N, M, row, col + 1, rest - 1);
        return live;
    }

    public static long gcd(long m, long n) {
        return n == 0 ? m : gcd(n, m % n);
    }

    public static String bob2(int N, int M, int i, int j, int K) {
        int[][][] dp = new int[N + 2][M + 2][K + 1];
        for (int row = 1; row <= N; row++) {
            for (int col = 1; col <= M; col++) {
                dp[row][col][0] = 1;
            }
        }
        for (int rest = 1; rest <= K; rest++) { //层数
            for (int row = 1; row <= N; row++) {
                for (int col = 1; col <= M; col++) {
                    dp[row][col][rest] = dp[row - 1][col][rest - 1];
                    dp[row][col][rest] += dp[row + 1][col][rest - 1];
                    dp[row][col][rest] += dp[row][col - 1][rest - 1];
                    dp[row][col][rest] += dp[row][col + 1][rest - 1];
                }
            }
        }
        long all = (long) Math.pow(4, K);
        long live = dp[i + 1][j + 1][K];
        long gcd = gcd(all, live);
        return String.valueOf((live / gcd) + "/" + (all / gcd));
    }

    public static void main(String[] args) {
        int N = 10;
        int M = 10;
        int i = 3;
        int j = 2;
        int K = 5;
        System.out.println(bob1(N, M, i, j, K));
        System.out.println(bob2(N, M, i, j, K));
    }
}

斜率优化

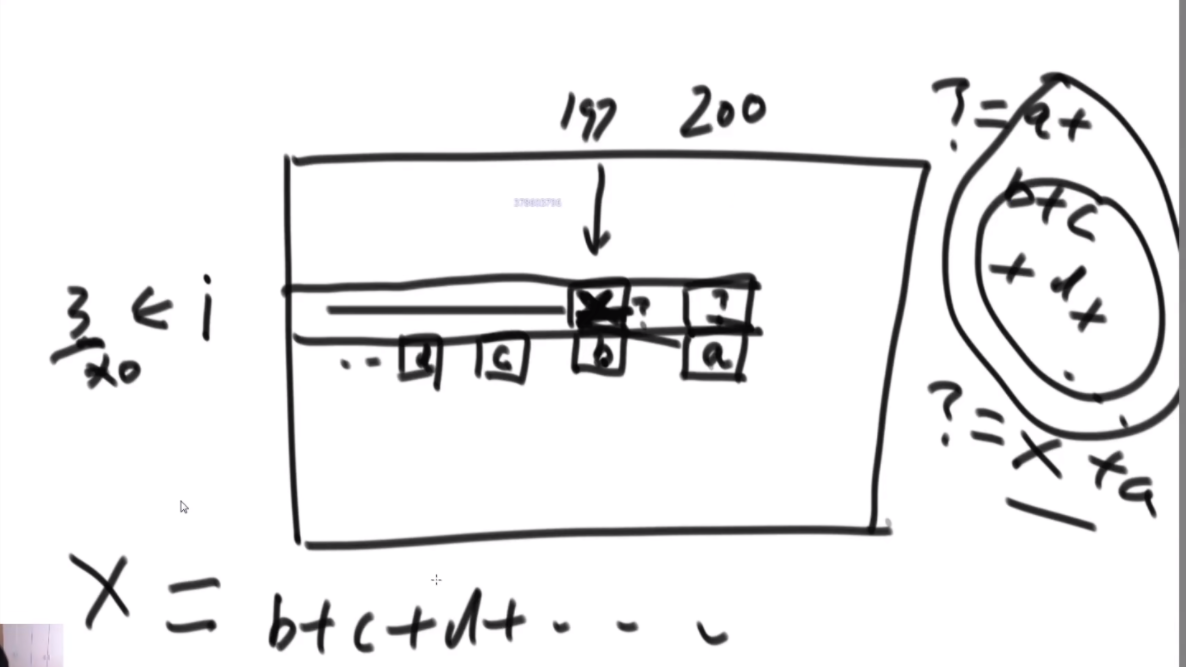
P17后面讲的内容就是Coinmin的原版差不多，带着循环数量的张数的表格。重点是完成严格表结构后，还完成了上图的斜率优化，可以对数组进行进一步的加速。原来的话是O(N*aim²) 现在就是O(Nxaim)，少了一个次方。

斜率优化原理：假设?=a+b+c+d+.. 已知？,那么x=?-a，因此可以少求一次b+c+d+..这个过程，因此少算了一边aim。减少了这一遍的枚举行为，从而完成优化。

尝试的评价准则：（1.可变参数的维度：int这种被称之为零维参数，数组的话会很复杂。2.可变参数个数：这个决定了表的维数，不多谈，尽量少） 从左到右、范围的尝试。

记忆化搜索：只是把递归用数组记录然后优化了一部分

严格表结构动态规划：通过表中数据的逻辑找到依赖关系，进一步的优化。

精致的DP：在严格表结构的情况下，加以观察可以进一步的优化，实战班里教个两三种完全够用，斜率优化就是其中一种。

p16:

暴力递归到动态规划

动态规划就是暴力尝试减少重复计算的技巧整，而已 这种技巧就是一个大型套路

先写出用尝试的思路解决问题的递归函数try(递归)，然后优化为记忆化搜索（dp），再优化为严格表结构(dp)，这个过程可能某些问题的时间复杂度是没有优化的，但是可以再优化为更加精致的严格表结构(dp)，这时可能会有更优化的时间复杂度，最关键的还是找到最开始的尝试。而不用操心时间复杂度 这个过程是无可替代的，没有套路的，只能依靠个人智慧，或者足够多的经验。

但是怎么把尝试的版本，优化成动态规划，是有固定套路的，大体步骤如下

1)找到什么可变参数可以代表一个递归状态，也就是哪些参数一旦确定，返回值就确定了

2)把可变参数的所有组合映射成一张表，有 1 个可变参数就是一维表，2 个可变参数就 是二维表，......

3)最终答案要的是表中的哪个位置，在表中标出

4)根据递归过程的 base case，把这张表的最简单、不需要依赖其他位置的那些位置填好 值

5)根据递归过程非base case的部分，也就是分析表中的普遍位置需要怎么计算得到，那 么这张表的填写顺序也就确定了

6)填好表，返回最终答案在表中位置的值

机器人达到指定位置方法数

【题目】

假设有排成一行的 N 个位置，记为 1~N，N 一定大于或等于 2。开始时机器人在其中的 M 位 置上(M 一定是 1~N 中的一个)，机器人可以往左走或者往右走，如果机器人来到 1 位置， 那 么下一步只能往右来到 2 位置;如果机器人来到 N 位置，那么下一步只能往左来到 N-1 位置。 规定机器人必须走 K 步，最终能来到 P 位置(P 也一定是 1~N 中的一个)的方法有多少种。给 定四个参数 N、M、K、P，返回方法数。

【举例】

N=5,M=2,K=3,P=3

上面的参数代表所有位置为 1 2 3 4 5。机器人最开始在 2 位置上，必须经过 3 步，最后到 达 3 位置。走的方法只有如下 3 种: (1) 从2到1，从1到2，从2到3 (2) 从2到3，从3到2，从2到3 (3) 从2到3，从3到4，从4到3 。所以返回方法数 3。

N=3,M=1,K=3,P=3

上面的参数代表所有位置为 1 2 3。机器人最开始在 1 位置上，必须经过 3 步，最后到达 3 位置。怎么走也不可能，所以返回方法数 0。

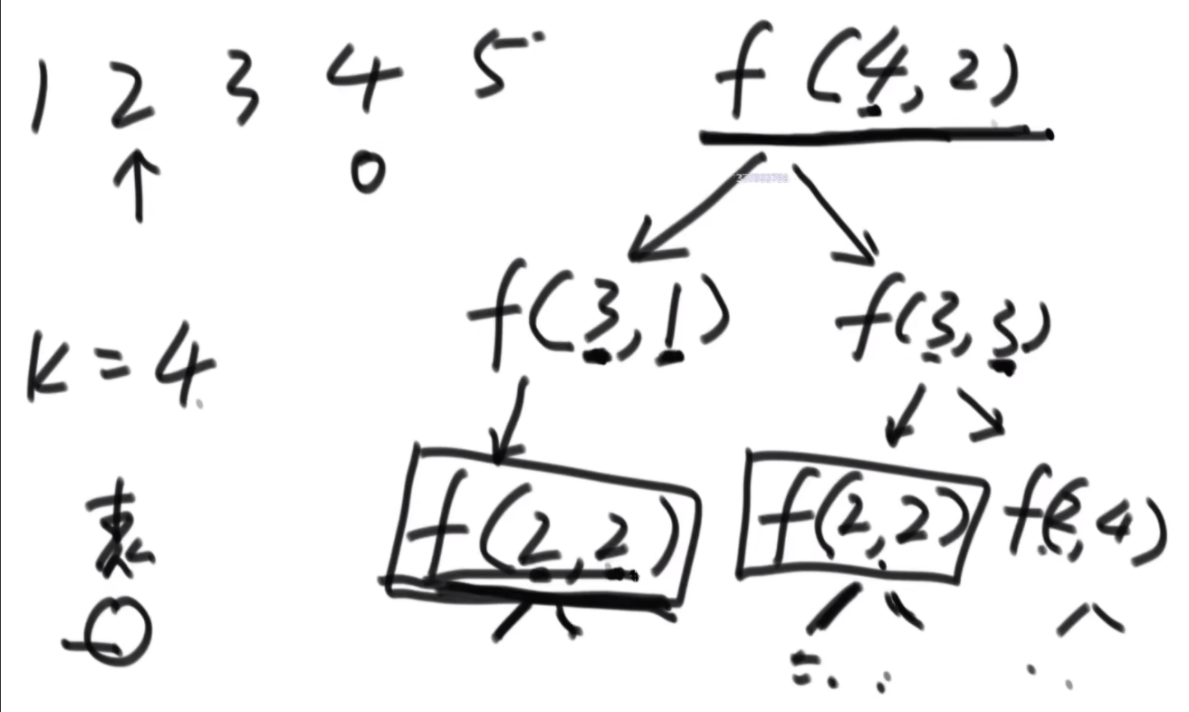
正常的递归，之所以被称之为暴力递归，就是因为会重复计算f(2,2)很多次，这里因为N,P是固定的，因此只有M,K是会动的，因为两个2，2的上级不一样，因此可以直接返回同样的结果再相加，因此这是无后效性的递归。可以建一个表去保留(2,2)的计算结果。

时间复杂度的计算，假如是暴力递归，那么是2^K因为有K步，每一步都可以展开。而记忆性搜索的复杂度为K*N，即剩余步数X总长度。

记忆性搜索只是一个单纯的缓存，而严格表结构有着依赖关系，不过这俩时间复杂度其实是一样的，只是没有依赖而已。

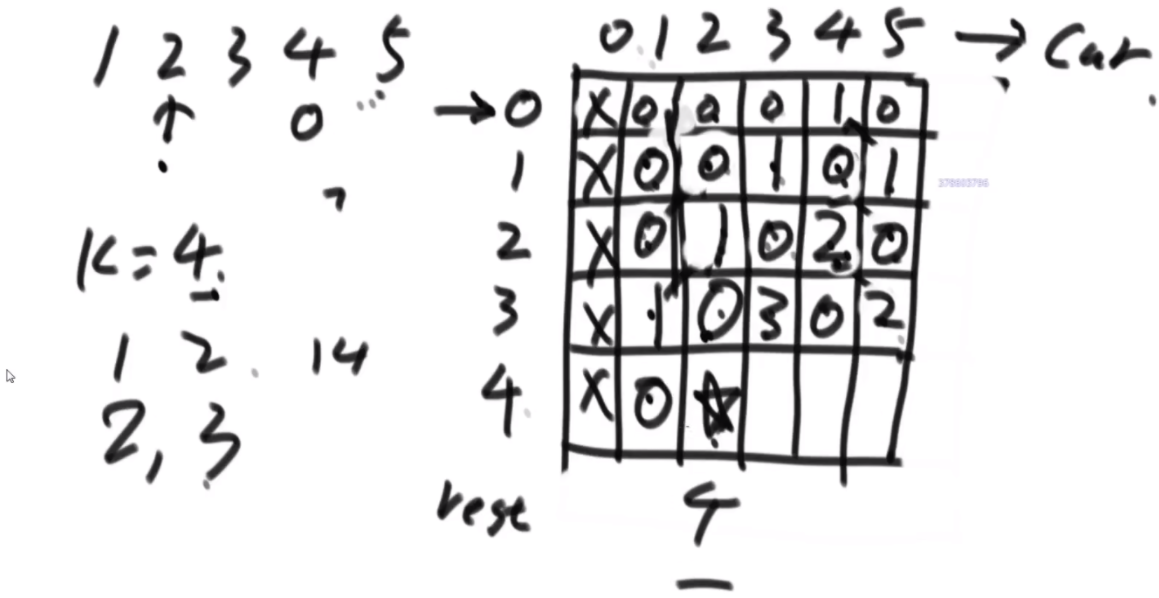
这里第二列依赖于它的右上角，最后一列依赖于左上角，中间的位置依赖于左上角+右上角，第一行结果是直接推出，因此可以直接得到所有信息。

package ZuoShen2.Class05;

public class RobotWalk {
    public static int ways1(int N, int M, int K, int P) {
        // 参数无效直接返回0
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        // 总共N个位置，从M点出发，还剩K步，返回最终能达到P的方法数
        return walk(N, M, K, P);
    }

    // N : 位置为1 ~ N，固定参数
    // cur : 当前在cur位置，可变参数
    // rest : 还剩res步没有走，可变参数
    // P : 最终目标位置是P，固定参数
    // 该函数的含义：只能在1~N这些位置上移动，当前在cur位置，走完rest步之后，停在P位置的方法数作为返回值返回
    public static int walk(int N, int cur, int rest, int P) {
        // 如果没有剩余步数了，当前的cur位置就是最后的位置
        // 如果最后的位置停在P上，那么之前做的移动是有效的
        // 如果最后的位置没在P上，那么之前做的移动是无效的
        if (rest == 0) {
            return cur == P ? 1 : 0;//有效就返回1 代表方法数+1 无效返回0
        }
        // 如果还有rest步要走，而当前的cur位置在1位置上，那么当前这步只能从1走向2
        // 后续的过程就是，来到2位置上，还剩rest-1步要走
        if (cur == 1) {
            return walk(N, 2, rest - 1, P);
        }
        // 如果还有rest步要走，而当前的cur位置在N位置上，那么当前这步只能从N走向N-1
        // 后续的过程就是，来到N-1位置上，还剩rest-1步要走
        if (cur == N) {
            return walk(N, N - 1, rest - 1, P);
        }
        // 如果还有rest步要走，而当前的cur位置在中间位置上，那么当前这步可以走向左，也可以走向右
        // 走向左之后，后续的过程就是，来到cur-1位置上，还剩rest-1步要走
        // 走向右之后，后续的过程就是，来到cur+1位置上，还剩rest-1步要走
        // 走向左、走向右是截然不同的方法，所以总方法数要都算上
        return walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);
    }

    public static int walks2(int N, int M, int K, int P){
        //即 可变参数的最大变化范围
        //剩余步数+1 最多这么个大小的一维  里面每一步的可能位置是N+1
        int[][] dp = new int[K + 1][N + 1];
        for (int i = 0; i <= K; i++) {
            for (int j = 0; j <= N; j++) {
                dp[i][j] = -1;//将默认值改为-1  因为初始值为0可能会混淆返回值的记录 0
            }
        }
        return ways2(N, M, K, P,dp);
    }


    //N 总节点  M当前位置  K剩余步数  P目标位置  
    //记忆化搜索
    public static int ways2(int N, int cur, int rest, int P, int[][] dp) {
        if(dp[rest][cur]!=-1){
            return dp[rest][cur];//当前位置算过，直接返回结果
        }
        //缓存没命中
        if(rest ==0){
            dp[rest][cur] = cur ==P?1:0;
            return dp[rest][cur];
        }
        // rest>0 有路可走
        if (cur == 1) {
            dp[rest][cur] = ways2(N, 2, rest - 1, P,dp );
        }else if(cur == N) {
            dp[rest][cur] = ways2(N, N - 1, rest - 1, P,dp);
        }else {
            dp[rest][cur] = ways2(N, cur + 1, rest - 1, P,dp) + ways2(N, cur - 1, rest - 1, P,dp);;
        }
        return dp[rest][cur];
    }

    //严格表结构  有数据间的依赖关系
    public static int ways3(int N, int M, int K, int P) {
        // 参数无效直接返回0
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        int[] dp = new int[N + 1];
        dp[P] = 1;
        for (int i = 1; i <= K; i++) {
            int leftUp = dp[1];// 左上角的值
            for (int j = 1; j <= N; j++) {
                int tmp = dp[j];
                if (j == 1) {
                    dp[j] = dp[j + 1];
                } else if (j == N) {
                    dp[j] = leftUp;
                } else {
                    dp[j] = leftUp + dp[j + 1];
                }
                leftUp = tmp;
            }
        }
        return dp[M];
    }

    public static void main(String[] args) {
        System.out.println(ways1(7, 4, 9, 5));
        System.out.println(walks2(7, 4, 9, 5));
        System.out.println(ways3(7, 4, 9, 5));
    }
}

换钱的最少货币数

【题目】 给定数组 arr，arr 中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值 的货币可以使用任意张，再给定一个整数 aim，代表要找的钱数，求组成 aim 的最少货币数。

【举例】

arr=[5,2,3]，aim=20。

4 张 5 元可以组成 20 元，其他的找钱方案都要使用更多张的货币，所以返回 4。

arr=[5,2,3]，aim=0。

不用任何货币就可以组成 0 元，返回 0。

arr=[3,5]，aim=2。

根本无法组成 2 元，钱不能找开的情况下默认返回-1。

这个题。。。左神讲的版本是一个面值的货币只能用一次，属于是简化版本了，不过思路是和上面一样的。

package ZuoShen2.Class05;

public class CoinsMin {
    public static int minCoins1(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return -1;
        }
        return process(arr, 0, aim);
    }

    // 当前考虑的面值是arr[i]，还剩rest的钱需要找零
    // 如果返回-1说明自由使用arr[i..N-1]面值的情况下，无论如何也无法找零rest
    // 如果返回不是-1，代表自由使用arr[i..N-1]面值的情况下，找零rest需要的最少张数
    public static int process(int[] arr, int i, int rest) {
        // base case：
        // 已经没有面值能够考虑了
        // 如果此时剩余的钱为0，返回0张
        // 如果此时剩余的钱不是0，返回-1
        if (i == arr.length) {
            return rest == 0 ? 0 : -1;
        }
        // 最少张数，初始时为-1，因为还没找到有效解
        int res = -1;
        // 依次尝试使用当前面值(arr[i])0张、1张、k张，但不能超过rest
        for (int k = 0; k * arr[i] <= rest; k++) {
            // 使用了k张arr[i]，剩下的钱为rest - k * arr[i]
            // 交给剩下的面值去搞定(arr[i+1..N-1])
            int next = process(arr, i + 1, rest - k * arr[i]);
            if (next != -1) { // 说明这个后续过程有效
                res = res == -1 ? next + k : Math.min(res, next + k);
            }
        }
        return res;
    }

    public static int minCoins2(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return -1;
        }
        int N = arr.length;
        int[][] dp = new int[N + 1][aim + 1];
        // 设置最后一排的值，除了dp[N][0]为0之外，其他都是-1
        for (int col = 1; col <= aim; col++) {
            dp[N][col] = -1;
        }
        for (int i = N - 1; i >= 0; i--) { // 从底往上计算每一行
            for (int rest = 0; rest <= aim; rest++) { // 每一行都从左往右
                dp[i][rest] = -1; // 初始时先设置dp[i][rest]的值无效
                if (dp[i + 1][rest] != -1) { // 下面的值如果有效
                    dp[i][rest] = dp[i + 1][rest]; // dp[i][rest]的值先设置成下面的值
                }
                // 左边的位置不越界并且有效
                if (rest - arr[i] >= 0 && dp[i][rest - arr[i]] != -1) {
                    if (dp[i][rest] == -1) { // 如果之前下面的值无效
                        dp[i][rest] = dp[i][rest - arr[i]] + 1;
                    } else { // 说明下面和左边的值都有效，取最小的
                        dp[i][rest] = Math.min(dp[i][rest],
                                dp[i][rest - arr[i]] + 1);
                    }
                }
            }
        }
        return dp[0][aim];
    }

    // for test
    public static int[] generateRandomArray(int len, int max) {
        int[] arr = new int[(int) (Math.random() * len) + 1];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) (Math.random() * max) + 1;
        }
        return arr;
    }

    public static void main(String[] args) {
        int len = 10;
        int max = 10;
        int testTime = 10000;
        for (int i = 0; i < testTime; i++) {
            int[] arr = generateRandomArray(len, max);
            int aim = (int) (Math.random() * 3 * max) + max;
            if (minCoins1(arr, aim) != minCoins2(arr, aim)) {
                System.out.println("ooops!");
                break;
            }
        }
    }
}

严格表结构动态规划流程

1. 先找到可变参数，如果有两个就是二维表 三个就是三维表 以此类推 表的初始化注意要减少干扰
2. 找到最终要终止的位置 这个位置 是主函数里面调用的范围对应到二维表上
3. 定义base case
4. 寻找到这几个的逻辑依赖
5. 按照顺序（把递归的copy过来改一改）

p15:

找出大数中所有重复的URL

有一个包含100亿个URL的大文件，假设每个URL占用64B，请找出其中所有重复的URL

可以哈希分流到多个文件，或者布隆过滤器，不过有错误率。

热门Top100

【补充】

某搜索公司一天的用户搜索词汇是海量的(百亿数据量)，请设计一种求出每天热门Top100词汇的可行办法。

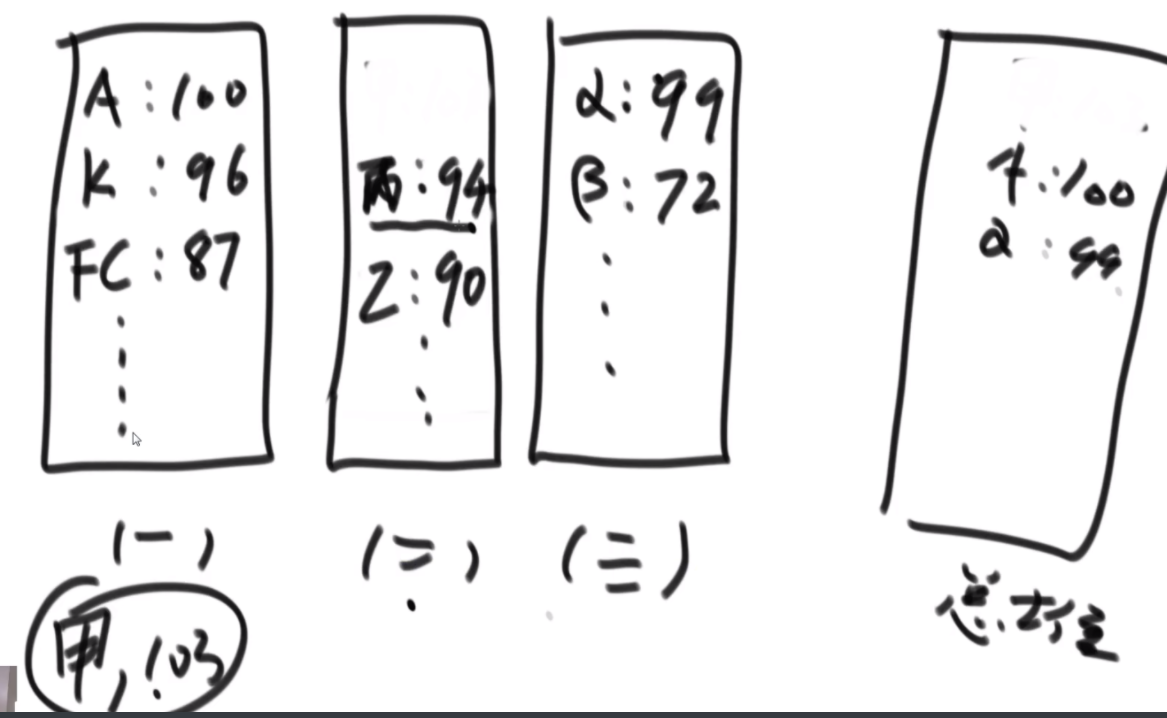
先给这些数据分流到小文件中进行排序，然后把它们组织成大根堆的形状，且key是元素，value是出现次数，按照value大小排序。这三个大根堆弹出3个堆顶，放入总堆中，在总堆中输出堆顶，然后知道这个堆顶是从哪个小堆中来的（假设是2号），那么再次把二号堆的堆顶放入总堆中，总堆中的元素数量保持3个不变。

可以理解为二维堆，调整代价比较低，而且都是log级别的。

找出所有出现了两次的数

32位无符号整数的范围是0~4294967295，现在有40亿个无符号整数，可以使用最多1GB的
内存，找出所有出现了两次的数。

万能的方法：哈希函数分流，计算1GB可以搞多大的HashMap（一个元素两个int,8字节），算一个哈希函数，%一个值，放入小文件中（相同的数，通过相同的哈希函数再取%一定会进入相同的小文件），在小文件中统计出现了两次的数，记录下来。

位图：原版是只能记录一次，现在需要升级一下。

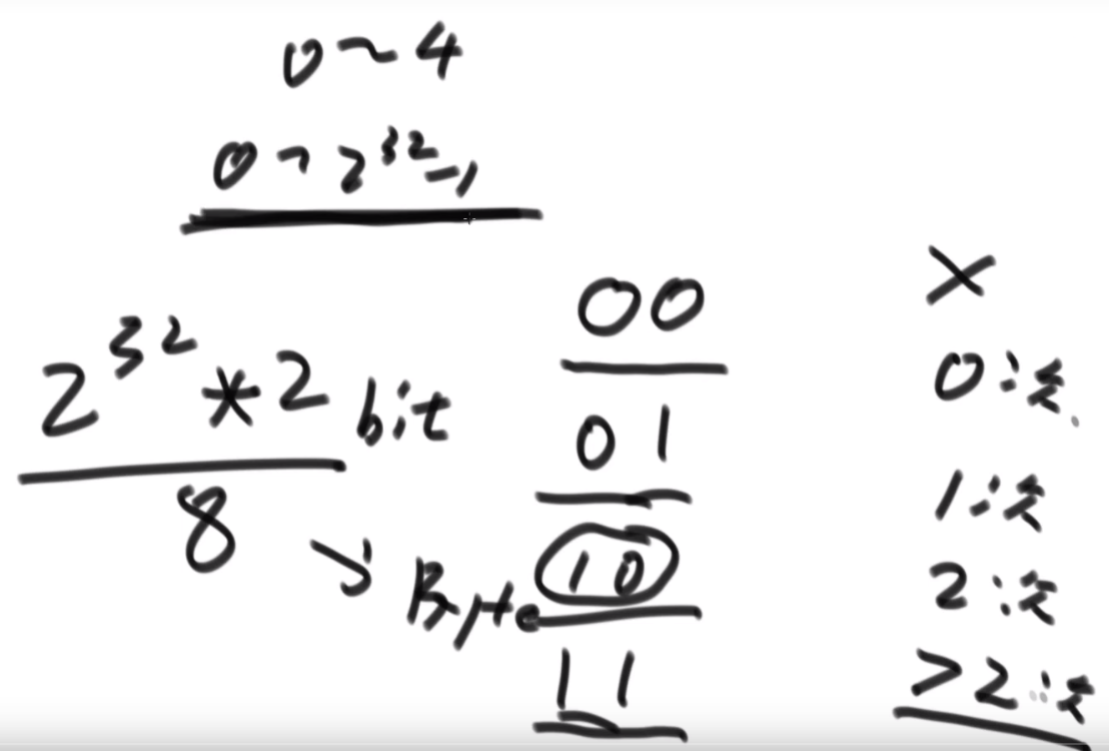
之前是用一位记录是否有，现在可以用两位，00代表没有出现过，01代表出现过一次，10代表出现了两次，11代表出现了两次以上。一共是2³²个数，需要2³²x2的位置，需要2³²x2/8个字节，小于1GB的空间。

【补充】

使用10MB的内存，找到40亿个整数的中位数

思路：这个题和p14中的找到没出现过的数类似，将10MB/4（4代表一个int有4字节，4B）分成2500份，这里选择2048个int的数组。令arr[0]代表，0到40亿/2048-1的范围，arr[1]代表，40亿/2048-1到40亿/2048*2-1的范围，以此类推。将arr[0]、arr[1]等顺序相加，直到超过20亿，那么中位数一定存在相加之后使总数量超过20亿的那个范围内，再次拆分那个范围。。

10G文件 5G内存 排序输出

腾讯的二面原题，

方法一：1GB是2³⁰B，（元素，出现次数）两个int组成的小根堆，这两个int8字节，假设算上索引空间啥的16字节，5GB/16=5x2²⁶ 认为是2²⁷好吧。无符号整数范围是-2³²~2³²-1，总共2³²个数，可以划分出2³²/2²⁷=2⁵个范围。

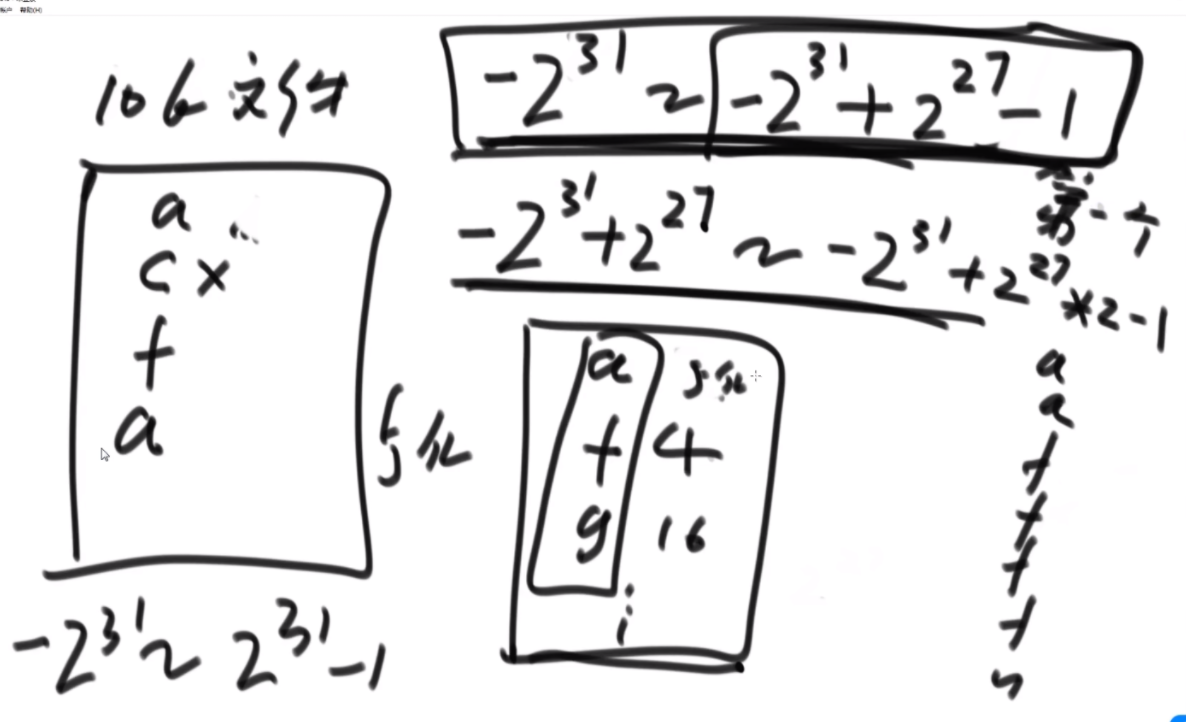
比如第一个范围就是-2³²~-2³²+2²⁷-1，那么遍历一遍这10个G的数据，将在第一个范围内的，放入一个小根堆中，（字符,出现次数），根据出现次数从小到大排序，遍历完这10个G的数据后，假设小根堆堆顶是(a,2)，那么输出2个a，以此类推。

方法二：

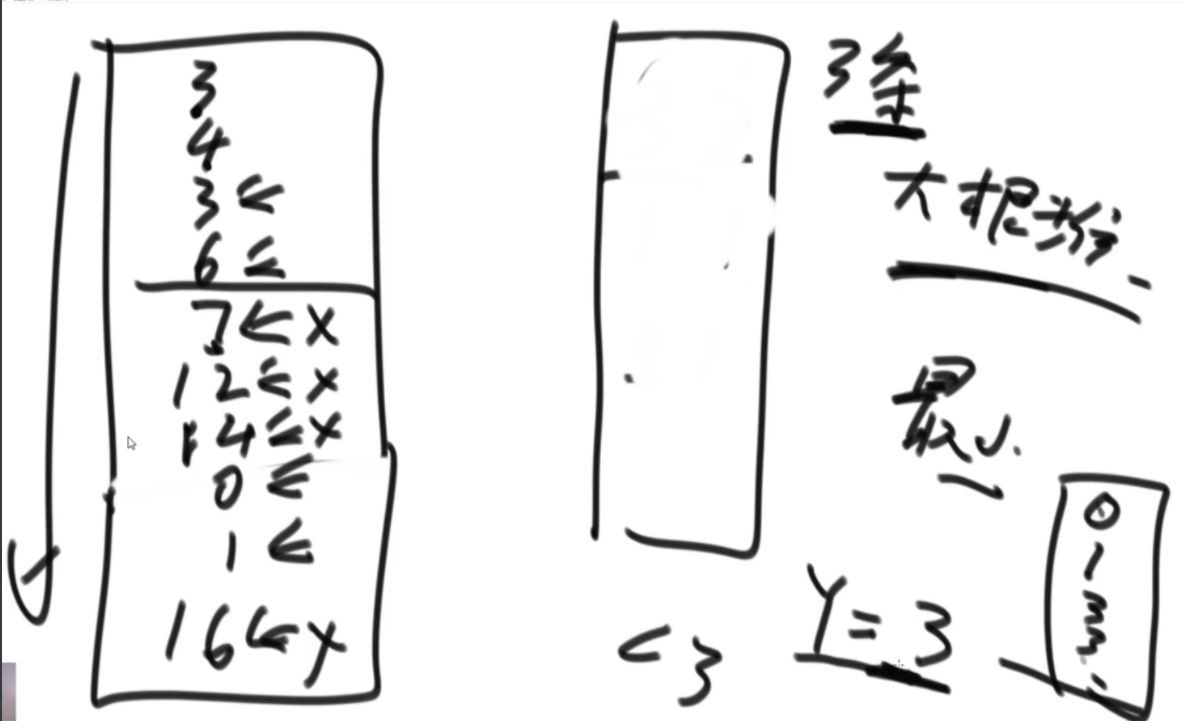
假设有12个数，一个大根堆最多能放3个数，从头开始遍历，一直到6是｛（6，1），（4，1），（3，2）｝，然后7、12、14因为大于大根堆的堆顶，因此不能进入，这大根堆中保存的是最小的3个数。当遇到0时，6被丢弃，然后进入0，当遇到1时，4被丢弃，然后进入1，得到这数组中最小的3个数顺序存起来。然后设置一个变量Y，Y=3，即3个最小的数中的最大的数，再遇到小于Y的数就不去管，再次遍历数组再获得剩下的元素中最小的三个数。以此类推。

通过这个5G可以判断出一个大根堆能放多少个元素。

大数据题目的解题技巧

资源限制类题目

1）哈希函数可以把数据按照种类均匀分流（均匀散列稳定） p11
2）布隆过滤器用于集合的建立与查询，并可以节省大量空间 p11
3）一致性哈希解决数据服务器的负载管理问题p11
4）利用并查集结构做岛问题的并行计算p12
5）位图解决某一范围上数字的出现情况，并可以节省大量空间p14
6）利用分段统计思想、并进一步节省大量空间p15
7）利用堆、外排序来做多个处理单元的结果合并p15

位运算：比较无符号32位整数

给定两个有符号32位整数a和b，返回a和b中较大的。

【要求】 不用做任何比较判断。

思路：见代码的注释

package ZuoShen2.Class05;

public class GetMax {
    //保证参数n不是1就是0的情况下，1->0,0->1
    public static int flip(int n) {
        return n ^ 1;
    }

    //n是非负数，返回1
    //n是负数，返回0
    public static int sign(int n) {
        return flip((n >> 31) & 1);
    }

    public static int getMax1(int a, int b) {
        int c = a - b;  //这个方法有问题，因为a-b可能会溢出
        int scA = sign(c);//a-b为非负，scA为1；a-b为负,scA为0
        int scB = flip(scA);//scA为0,scB为1;scA为1,scB为0
        //scA为0,scB必为1;scA为1,scB必为0
        return a * scA + b * scB;
    }

    //优化方法
    public static int getMax2(int a, int b) {
        int c = a - b;//c依旧可能溢出 一个正的2的32次方-1  -  一个负的2的32次方-1 直接溢出
        int sa = sign(a);
        int sb = sign(b);
        int sc = sign(c);
        int difSab = sa ^ sb; //a和b的符号不一样为1，一样为0 ^为异或
        int sameSab = flip(difSab);//a和b的符号不一样为0，一样为1
        //difSab和difSab互斥  中一个 返回a
        int returnA = difSab * sa + sameSab * sc; //如果a b符号相同，不可能溢出 a-b>=0返回a
        //返回B的条件和返回A的条件互斥
        int returnB = flip(returnA);//如果a和b符号不相同，还得有a是非负 返回a，此时b小于0，一定小于a
        return a * returnA + b * returnB;
    }

    public static void main(String[] args) {
        int a = -16;
        int b = 1;
        System.out.println(getMax1(a, b));
        System.out.println(getMax2(a, b));
        a = 2147483647;
        b = -2147480000;
        System.out.println(getMax1(a, b)); // wrong answer because of overflow
        System.out.println(getMax2(a, b));

    }
}

位运算：判断数是否为2的幂

判断一个32位正数是不是2的幂、4的幂

判断数是不是2的幂两个方法：第一个方法：x&(x-1)==0，第二个方法：pos & (~pos + 1);（取反+1）&原码，得到最右侧的1，如果只有一个，那么是2的幂。

判断数是不是4的幂两个方法：首先只能有一个1，其次它的1只能在0 2 4 8这种位置上.第一步：判断是不是只有一个1，第二步：x & 010101...01 ！= 0 ，那么是。因为如果不等于0意味着它的1在偶数次位上。

package ZuoShen2.Class05;

public class Power {
    public static boolean is2Power(int n) {
        return (n & (n - 1)) != 0;
    }

    public static boolean is4Power(int n) {
                                        //010101...010101
        return (n & (n - 1)) != 0 && (n & 0x55555555) != 0;
    }
}

位运算：位运算完成加减乘除

给定两个有符号32位整数a和b，不能使用算术运算符，分别实现a和b的加、减、乘、除运 算

【要求】 如果给定a、b执行加减乘除的运算结果就会导致数据的溢出，那么你实现的函数不必对此 负责，除此之外请保证计算过程不发生溢出

加法思路：

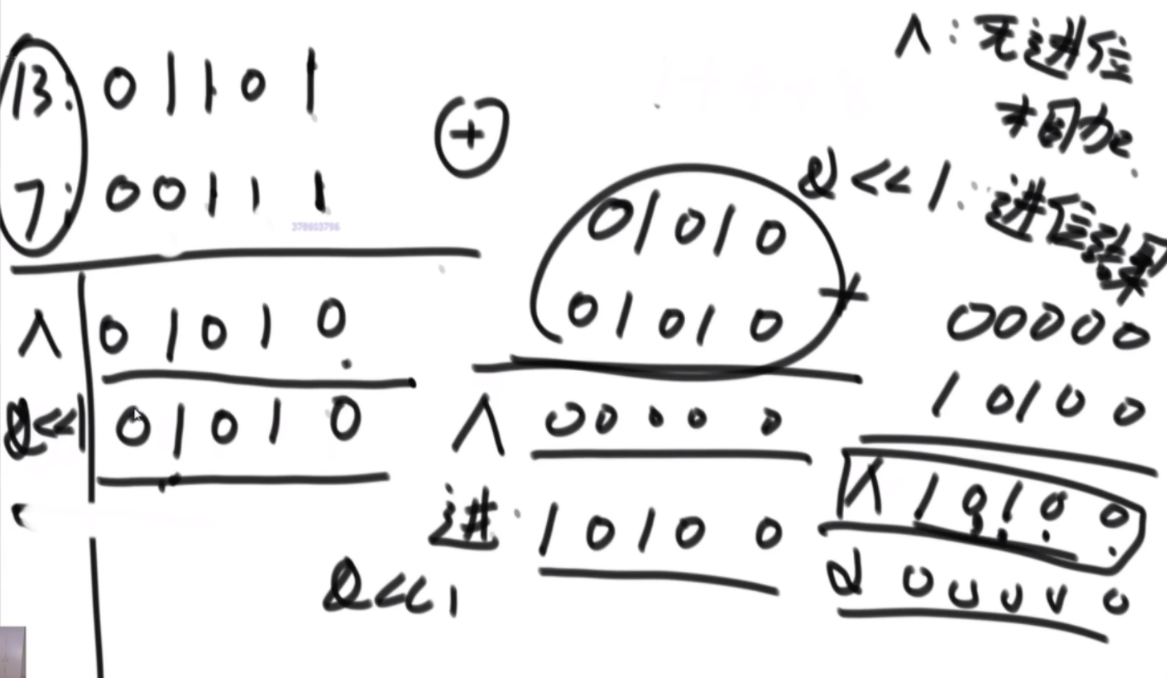
^(异或):又称无进位相加，相异为1，相同为0。&可以获得进位信息，那么&后左移一位，就可以将进位信息对应到应该在的位置，那么两数相加等价于，异或的结果和&<<1的结果相加，对这两个结果再次进行异或和&<<1，知道&<<1的进位信息为0，即这次相加没有进位，则异或的结果就是和的结果。

减法思路：减法就是a+（-b） 如何获得相反数？ b取反再加1（补码）

乘法思路：每走一次a左移一位，b右移一位，a左移 是因为乘法的每一个循环要加的数都左移一位，b右移是为了获得新的末尾。

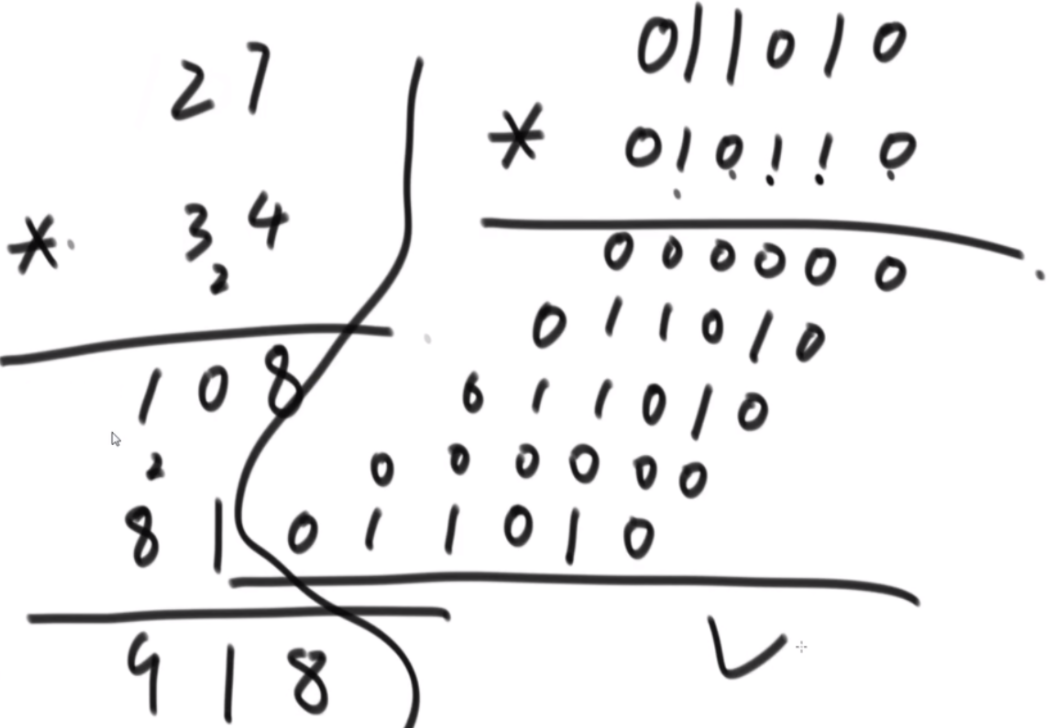
除法思路：

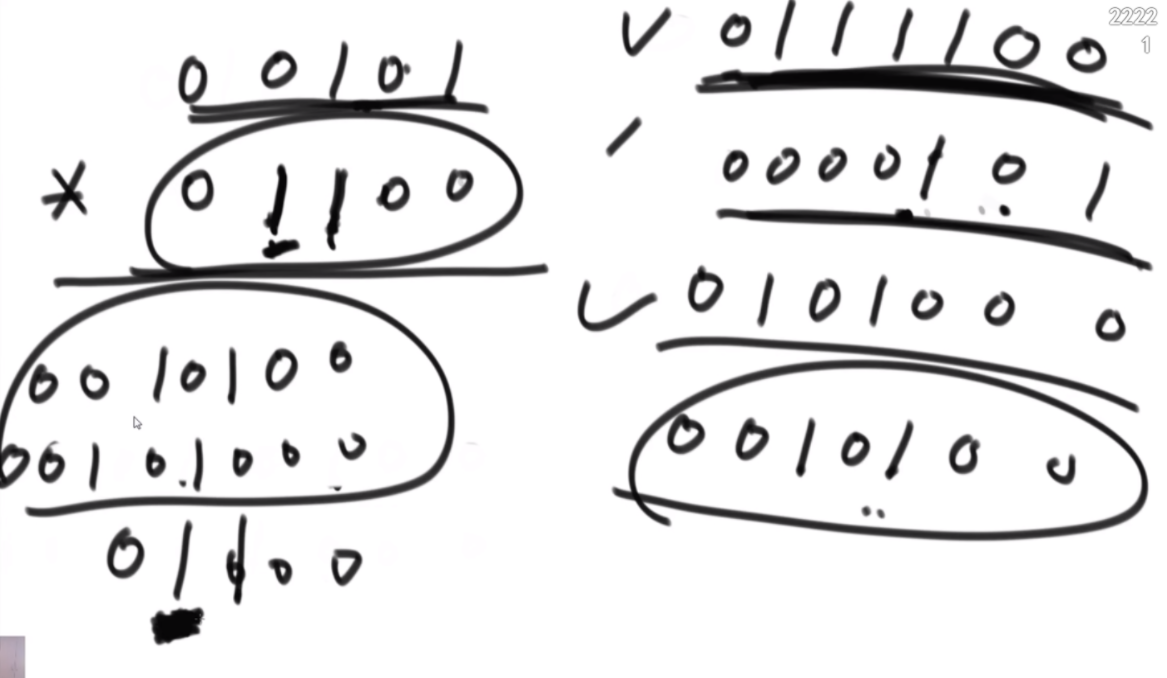
这个角度得从乘法的逆来看，乘法的方法是下面的数左移再*1相加，因此除法的第一步是把除数尽量左移，但不能超过被除数，然后被除数-除数，得到下一次循环的被除数，除数不变，继续循环这个操作，直到被除数=0。另一个方法：a试试能不能减掉b左移31位的结果，如果不能试试30，假如试到左移4位的时候可以减了，那么这一位一定为1，结果一定有一个10000，将a更新为a-b左移4位的结果，继续，可以获得所有因子，假设剩到最后一位除不尽，此时b左移0位依旧不行，那么这一位本来就是会被舍弃的位，不用管它。

package ZuoShen2.Class05;

public class AddMinusMultiDivideByBit {

    //如果，用户传入的参数，a+b就是溢出的，用户活该。。。
    public static int add(int a, int b) {
        int sum = a;
        while (b != 0) {
            sum = a ^ b; //无进位相加
            b = (a & b) << 1; //进位信息
            a = sum;
        }
        return sum;
    }
    //获得相反数
    public static int negNum(int n) {
        return add(~n, 1);
    }

    public static int minus(int a, int b) {
        //减法就是a+（-b） 如何获得相反数？  b取反再加1（补码）
        return add(a, negNum(b));
    }

    //如果，用户传入的参数，a*b就是溢出的，用户活该。。。
    public static int multi(int a, int b) {
        int res = 0;
        while (b != 0) {
            if ((b & 1) != 0) { //b的最后位置元素是否为1
                res = add(res, a);
            }
            a <<= 1;  //每走一次a左移一位，b右移一位
            b >>>= 1; //a左移 是因为乘法的每一个循环要加的数都左移一位，b右移是为了获得新的末尾
        }
        return res;
    }

    public static boolean isNeg(int n) {
        return n < 0;
    }

    public static int div(int a, int b) {
        int x = isNeg(a) ? negNum(a) : a;
        int y = isNeg(b) ? negNum(b) : b;
        int res = 0;
        for (int i = 31; i > -1; i = minus(i, 1)) {
            if ((x >> i) >= y) { //y左移可能会溢出，因此选择x去左移
                                //当然最后运算的时候还是y左移，只是用x去右移来找到i
                res |= (1 << i);
                x = minus(x, y << i);
            }
        }
        return isNeg(a) ^ isNeg(b) ? negNum(res) : res;
    }

    public static int divide(int a, int b) {
        if (b == 0) {
            throw new RuntimeException("divisor is 0");
        }
        if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
            return 1;
        } else if (b == Integer.MIN_VALUE) {
            return 0;
        } else if (a == Integer.MIN_VALUE) {
            int res = div(add(a, 1), b);
            return add(res, div(minus(a, multi(res, b)), b));
        } else {
            return div(a, b);
        }
    }

    public static void main(String[] args) {
        int a = (int) (Math.random() * 100000) - 50000;
        int b = (int) (Math.random() * 100000) - 50000;
        System.out.println("a = " + a + ", b = " + b);
        System.out.println(add(a, b));
        System.out.println(a + b);
        System.out.println("=========");
        System.out.println(minus(a, b));
        System.out.println(a - b);
        System.out.println("=========");
        System.out.println(multi(a, b));
        System.out.println(a * b);
        System.out.println("=========");
        System.out.println(divide(a, b));
        System.out.println(a / b);
        System.out.println("=========");

        a = Integer.MIN_VALUE;
        b = 32;
        System.out.println(divide(a, b));
        System.out.println(a / b);

    }
}

p14:

二叉树节点间的最大距离问题

从二叉树的节点a出发，可以向上或者向下走，但沿途的节点只能经过一次，到达节点b时路径上的节点个数叫作a到b的距离，那么二叉树任何两个节点之间都有距离，求整棵树上的最大距离。

思路：分情况讨论，看根节点是否在最大距离的路径里。如果根节点x不参与，要么最大距离在左子树要么最大距离在右子树上，如果根节点参与，那么最大距离应该为左子树离x最远的节点+1（根节点x）+右子树离x最远的节点。最大距离肯定是这三个值取max。

    public static class ReturnType{
        public int maxDistance;
        public int h;

        public ReturnType(int m, int h) {
            this.maxDistance = m;;
            this.h = h;
        }
    }

    //返回以x为头的整棵树，两个信息
    public static ReturnType process(Node head) {
        if(head == null) {
            return new ReturnType(0,0);
        }
        ReturnType leftReturnType = process(head.left);
        ReturnType rightReturnType = process(head.right);
        //可能性1 2 3   获取左右子树的返回值 然后整合信息
        int p1 = leftReturnType.maxDistance;
        int p2 = rightReturnType.maxDistance;
        int includeHeadDistance = leftReturnType.h + 1 + rightReturnType.h;
        int resultDistance = Math.max(Math.max(p1, p2), includeHeadDistance);
        int hitself  = Math.max(rightReturnType.h, leftReturnType.h) + 1;
        return new ReturnType(resultDistance, hitself);
    }

派对的最大快乐值

员工信息的定义如下:
class Employee {
public int happy; // 这名员工可以带来的快乐值
List subordinates; // 这名员工有哪些直接下级
}
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的
多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有
任何下属的基层员工(subordinates列表为空)，除基层员工外，每个员工都有一个或多个直接下级。
这个公司现在要办party，你可以决定哪些员工来，哪些员工不来。但是要遵循如下规则。
1.如果某个员工来了，那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

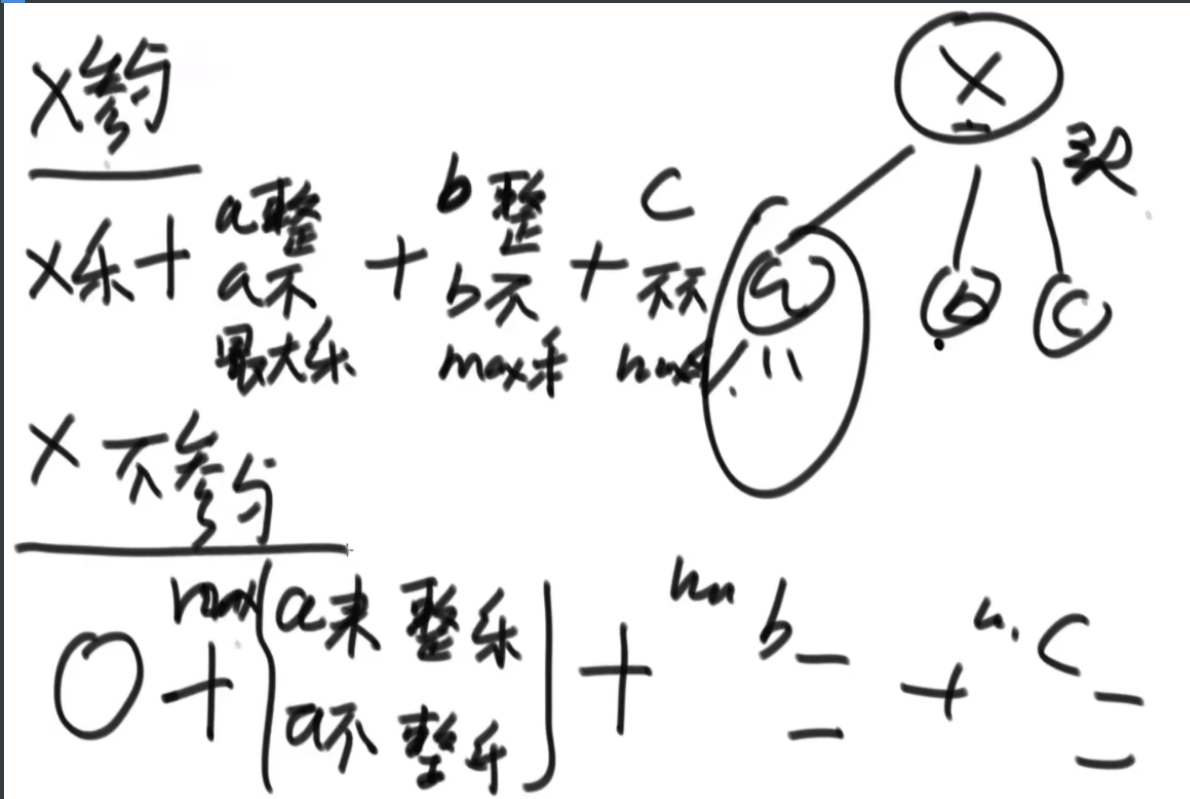
思路：分情况讨论，依旧是看头结点是否参与。如果头结点来，那么结果为x的快乐值+a不来a整棵树的最大快乐值+b不来b整棵树的最大快乐值+c不来c整棵树的最大快乐值；如果头结点不来，那么结果为0+max(a来的话整棵树的最大快乐值，a不来的话整棵树的最大快乐值)+max(b来的话整棵树的最大快乐值，b不来的话整棵树的最大快乐值)+max(c来的话整棵树的最大快乐值，c不来的话整棵树的最大快乐值)

package ZuoShen2.Class04;

import java.util.List;

public class MaxHappy {
    public static class Employee{
        public int happy;
        public List<Employee> nexts;
    }

    public static class Info{
        public int laiMaxHappy;
        public int buMaxHappy;
        public Info(int lai,int bu){
            laiMaxHappy=lai;
            buMaxHappy=bu;
        }
    }
    public static int maxHappy(Employee boss){
        Info headInfo = process(boss);
        return Math.max(headInfo.laiMaxHappy,headInfo.buMaxHappy);
    }

    public static Info process(Employee x){
        //base case
        if(x.nexts.isEmpty()){ //x是最基层员工的时候
            return new Info(x.happy,0);
        }
        int lai = x.happy; //x来的情况下，整棵树的最大收益
        int bu = 0; //x不来的情况下，整棵树的最大收益
        for(Employee next:x.nexts){
            Info nextInfo = process(next);
            //x来了的话，直接下级就来不了  所以加上buMaxHappy
            lai += nextInfo.buMaxHappy;
            //x不来了的话  取下级来和不来的最大快乐值
            bu += Math.max(nextInfo.laiMaxHappy,nextInfo.buMaxHappy);
        }
        return new Info(lai,bu  );
    }

}

Morris遍历

一种遍历二叉树的方式，并且时间复杂度O(N)，额外空间复杂度O(1).通过利用原树中大量空闲指针的方式，达到节省空间的目的。线索二叉树

Morris遍历细节
假设来到当前节点cur，开始时cur来到头节点位置
1）如果cur没有左孩子，cur向右移动(cur = cur.right)
2）如果cur有左孩子，找到左子树上最右的节点mostRight：
a.如果mostRight的右指针指向空，让其指向cur，然后cur向左移动(cur = cur.left)
b.如果mostRight的右指针指向cur，让其指向null，然后cur向右移动(cur = cur.right)
3）cur为空时遍历停止

左树上的最右孩子：遍历cur=cur.right，直到cur.right=null。左树上的右边界同理。

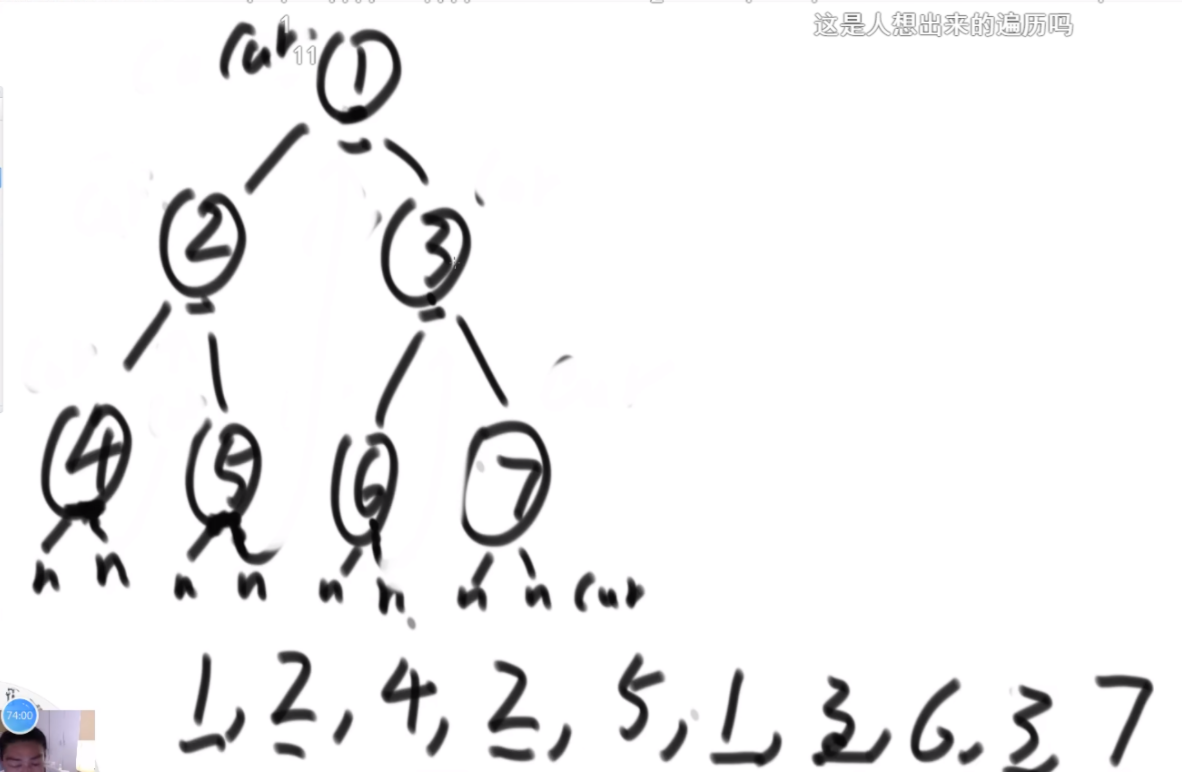
这里cur从1开始，让5的右指针指向1，cur来到2，4的右指针指向2，cur走向4，此时没有左孩子，cur再次来到2，有左孩子，让4的右指针指向null，cur向右移动来到5，依次类推。因此如果一个节点有左子树，那么这个节点会被走过两次，第二次是通过左子树最右侧节点的右指针指向自己，回到自己后再把指针修改回去。

为什么找到左子树的最右节点不会增加时间复杂度？

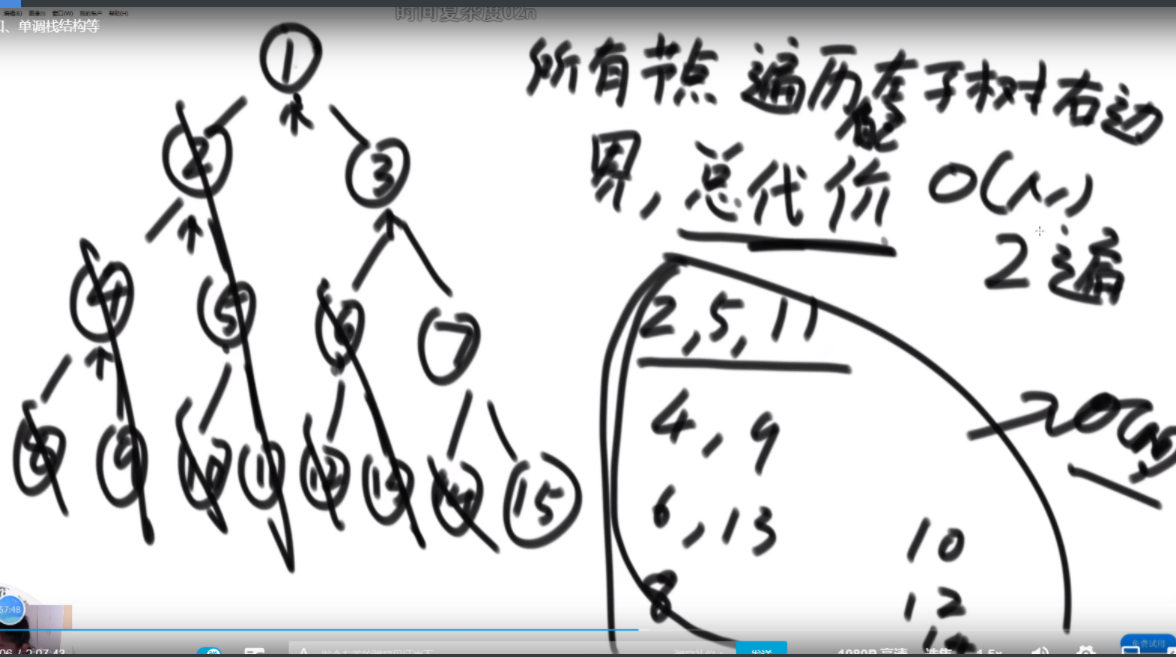
如上图，总代价最多也就是毕竟整个数的节点数量，N，因为要走两遍所以是2*N，因此总代价还是O(N)的。

先序遍历：第一次遇到有左子树的节点的时候打印，没有左子树的直接打印。

中序遍历：第二次遇到有左子树的节点的时候打印，没有左子树的节点直接打印。

后序遍历：因为Morris遍历最多只能到达一个节点两次，因此后序遍历比较复杂。首先，遇到没有左树的节点跳过，第二次遇到有左树的节点，逆序打印其左子树的右边界，最后结束的时候逆序打印整棵树的右边界。

如何逆序打印右边界：先把从头开始给它右边界逆序，（单链表的逆序），打印完再逆序回去。

如果需要第三次到达这个节点，那么最优解就是传统的递归，如果不需要，最优解就是Morris遍历。

代码：

package ZuoShen2.Class04;

public class MorrisTraversal {
    public static class Node {
        public int value;
        Node left;
        Node right;

        public Node(int data) {
            this.value = data;
        }
    }
    //中序遍历
    public static void morrisIn(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {  // 过流程，cur为空结束
            mostRight = cur.left;  //mostRight是cur左孩子
            if (mostRight != null) {  // cur有左子树
                //原本是指向null  但是也有可能修改后指向cur 找到任意一种情况就停
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                //mostRight变成左树上的最右节点
                if (mostRight.right == null) { //第一次来到cur节点
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {//第二次来到cur节点，把指针弄回去然后往右走
                    mostRight.right = null;
                }
            }
            System.out.print(cur.value + " ");
            //如果cur没有左孩子 直接往右走  情况1
            cur = cur.right;
        }
        System.out.println();
    }
    //先序遍历
    public static void morrisPre(Node head) {
        if (head == null) {
            return;
        }
        Node cur1 = head;
        Node cur2 = null;
        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;
                }
                if (cur2.right == null) {
                    cur2.right = cur1;
                    System.out.print(cur1.value + " ");//先序遍历
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;
                }
            } else {
                System.out.print(cur1.value + " ");
            }
            cur1 = cur1.right;
        }
        System.out.println();
    }

    public static void morrisPos(Node head) {
        if (head == null) {
            return;
        }
        Node cur1 = head;
        Node cur2 = null;
        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;
                }
                if (cur2.right == null) {
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;
                    printEdge(cur1.left);
                }
            }
            cur1 = cur1.right;
        }
        printEdge(head);
        System.out.println();
    }

    public static void printEdge(Node head) {
        Node tail = reverseEdge(head);
        Node cur = tail;
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        reverseEdge(tail);
    }

    public static Node reverseEdge(Node from) {
        Node pre = null;
        Node next = null;
        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }
    //Morris 中序遍历
    public static boolean isBST(Node head) {
        if (head == null) {
            return true;
        }
        Node cur = head;
        Node mostRight = null;
        int preValue = Integer.MIN_VALUE;
        while (cur != null) {  // 过流程，cur为空结束
            mostRight = cur.left;  //mostRight是cur左孩子
            if (mostRight != null) {  // cur有左子树
                //原本是指向null  但是也有可能修改后指向cur 找到任意一种情况就停
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                //mostRight变成左树上的最右节点
                if (mostRight.right == null) { //第一次来到cur节点
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {//第二次来到cur节点，把指针弄回去然后往右走
                    mostRight.right = null;
                }
            }
//            System.out.print(cur.value + " ");
            //把打印输出改成比较
            if (cur.value <= preValue) {
                return false;
            }
            //如果cur没有左孩子 直接往右走  情况1
            preValue= cur.value;
            cur = cur.right;
        }
        return true;
    }
    // for test -- print tree
    public static void printTree(Node head) {
        System.out.println("Binary Tree:");
        printInOrder(head, 0, "H", 17);
        System.out.println();
    }

    public static void printInOrder(Node head, int height, String to, int len) {
        if (head == null) {
            return;
        }
        printInOrder(head.right, height + 1, "v", len);
        String val = to + head.value + to;
        int lenM = val.length();
        int lenL = (len - lenM) / 2;
        int lenR = len - lenM - lenL;
        val = getSpace(lenL) + val + getSpace(lenR);
        System.out.println(getSpace(height * len) + val);
        printInOrder(head.left, height + 1, "^", len);
    }

    public static String getSpace(int num) {
        String space = " ";
        StringBuffer buf = new StringBuffer("");
        for (int i = 0; i < num; i++) {
            buf.append(space);
        }
        return buf.toString();
    }

    public static void main(String[] args) {
        Node head = new Node(4);
        head.left = new Node(2);
        head.right = new Node(6);
        head.left.left = new Node(1);
        head.left.right = new Node(3);
        head.right.left = new Node(5);
        head.right.right = new Node(7);
        printTree(head);
        morrisIn(head);
        morrisPre(head);
        morrisPos(head);
        printTree(head);

    }
}

树形DP的再次讲解

先将题目分成两个子树，让左右子树同时返回相同类型的值，然后生成以该节点为根的树的returnData 依次递归

一大分类方式：看头结点是否参与

位图解决某一范围上数字的出现情况

32位无符号整数的范围是0~4,294,967,295 (0~2³²-1)，现在有一个正好包含40亿个无符号整数的文件，所以在整个范围中必然存在没出现过的数。可以使用最多1GB的内存，怎么找到所有未出现过的数？（Bitmap?）

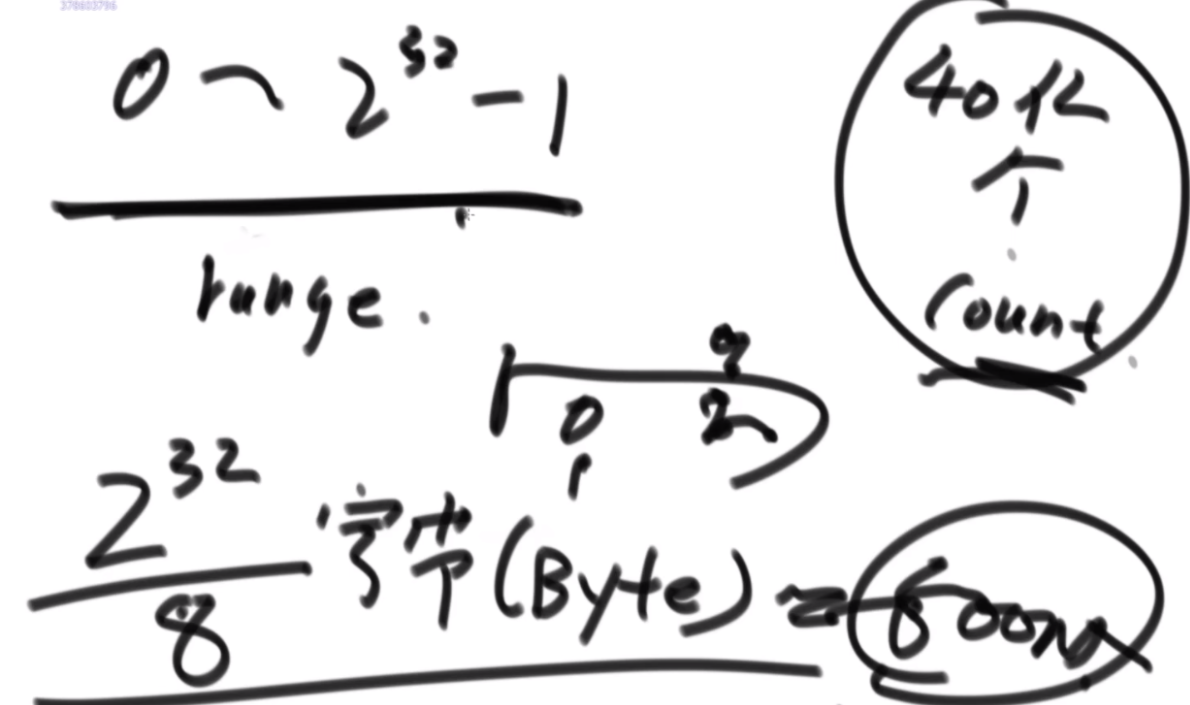
正常思路：类似于BitMap的原理，一个int 4字节32位，因此一字节是8位，即11111111，因此可以用这500M的空间表示。

【进阶】

内存限制为 10MB，但是只用找到一个没出现过的数即可

进阶思路：现在假设内存限制为3KB，一个无符号数为4字节，3000/4=700+个，因此创建一个512大小的int数组一定没问题，数字范围为0~2³²-1，那么2³²一定可以整除512(2⁹) = 8388608，现在这个数组中0位置上表示的是0~8388608这个范围的数字出现了多少个，1位置就是8388608+1到8388608*2这个范围的数字出现了多少个，2位置以后以此类推，存的就是x/8388608，假设结果为23，那么arr[23]位置的数字++，总会有一个位置的数字数量没有达到8388608个，那么就知道那个数字在哪个范围上了，然后再次细分范围，对这个范围除个512，对这40亿个数字再次遍历，只要这个范围中的数字，周而复始，总能定位到这个数字。利用词频统计一定会不够这一特点。

假设只有有限个变量：

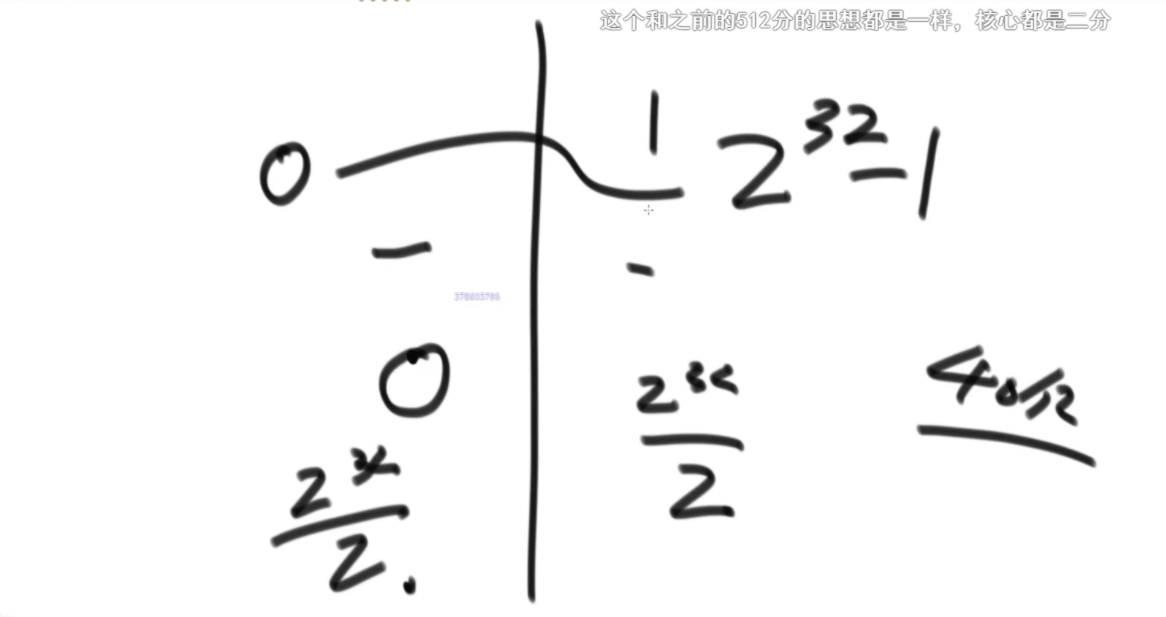
就二分，然后遍历，看左右两边哪边不够2³²/2个，再对这边进行二分，继续遍历统计，一直二分，二分32次（等价于那个数组中的512分）。

p13:

Manacher算法

Manacher算法解决的问题：字符串str中，最长回文子串的长度如何求解？
如何做到时间复杂度O(N)完成？

最长回文子串：回文就是正着念和反着念是一样的 最长就是找到最长的

例子：'abc12320de1' 中 最长回文子串就是'232' “abcba” "abba"

暴力解法：遍历每个位置，每个位置往左右两边去寻找，判断回文长度。缺陷：无法找到偶数长度的回文。

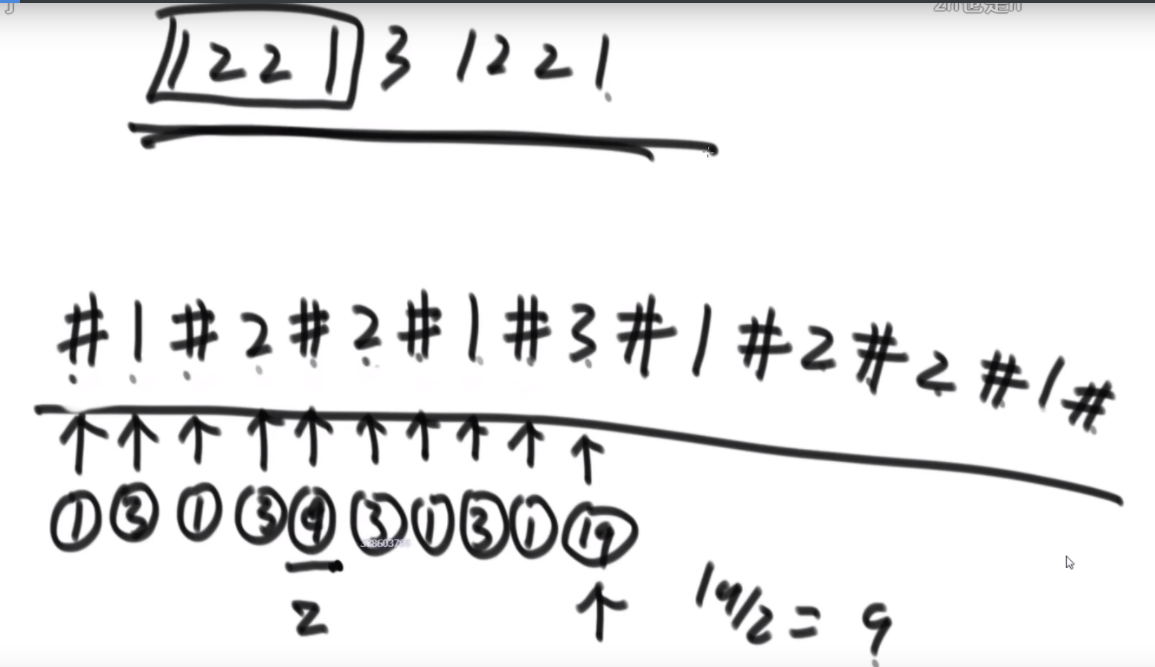
优化解法（如上图）：给每个位置左右两侧填充'#'字符，然后再判断每个位置的回文长度，最终每个位置结果除以2，就是结果。这个特殊字符可以是任意字符，和字符串中重复也没事。因为这个字符只是辅助。时间复杂度O(n²)，举例："11111111"。

Manacher算法（马拉车）可以加速到O(n)。这里需要介绍这个算法所用到的概念：

1. 回文直径：这个位置的回文长度，回文半径：这个位置走向直径结束的位置的长度。组成一个数组。
2. 最远边界位置：R初始为-1，目前回文直径走到过的最远的右侧的位置。变量
3. 更远边界的中心距离：C初始为-1，取得更远中心边界时，中心点在哪里。变量

算法详解： 首先填充'#'

1. 当当前位置没有超过R的时候，直接暴力解法。

2. 来到当前位置，即中心点在R内时，假设当前位置为i，此时C在i左侧，根据C对i和R做对称，得到i'和L。在2的大情况下，根据i'的回文状况再细分。

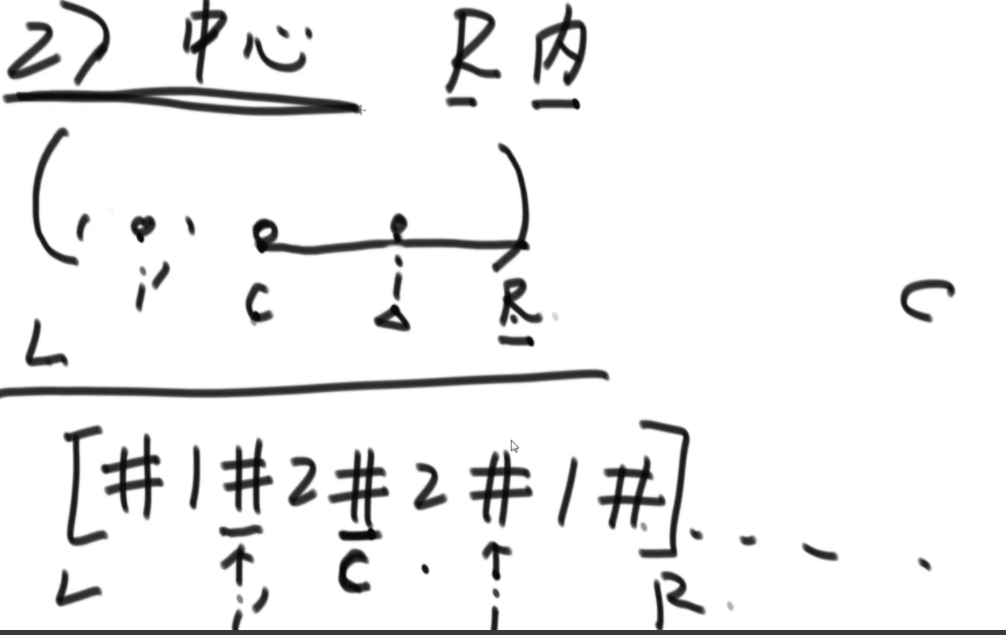
   • 2情况下的第一种情况，i'的回文区域在L..R里面，那么i的回文半径等于i'的回文半径。（原因，）

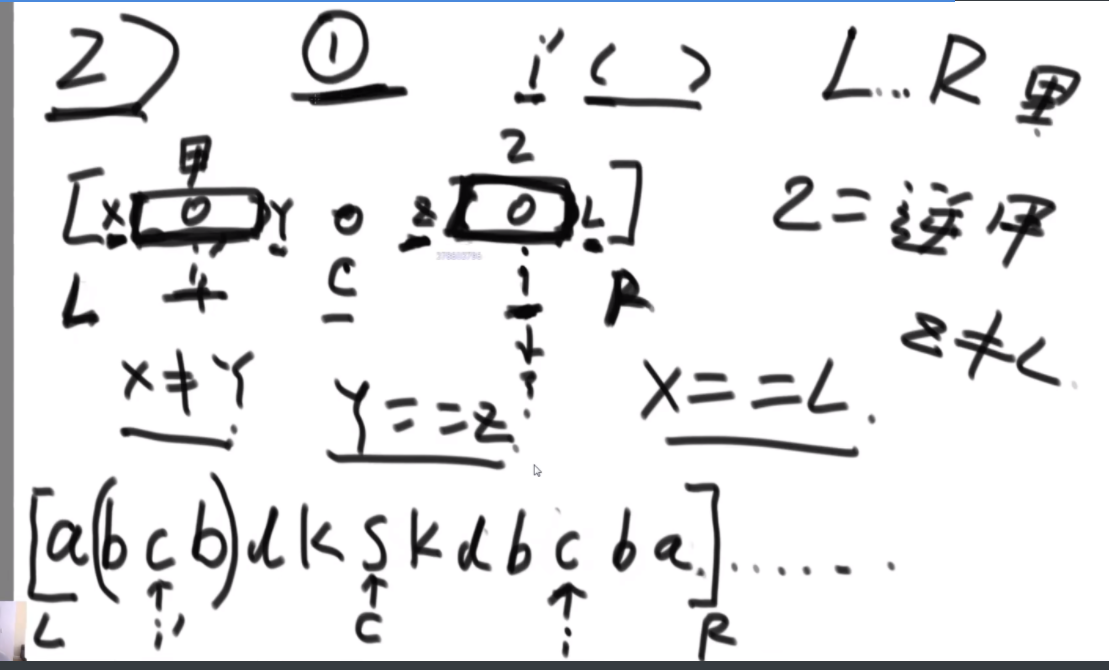
     证明：甲和乙是对称的，因此X≠Y,Z≠L,所以半径相同。

   • 2情况下的第二种情况，i'的回文区域在L..R外面那么i的回文半径等于i~R。

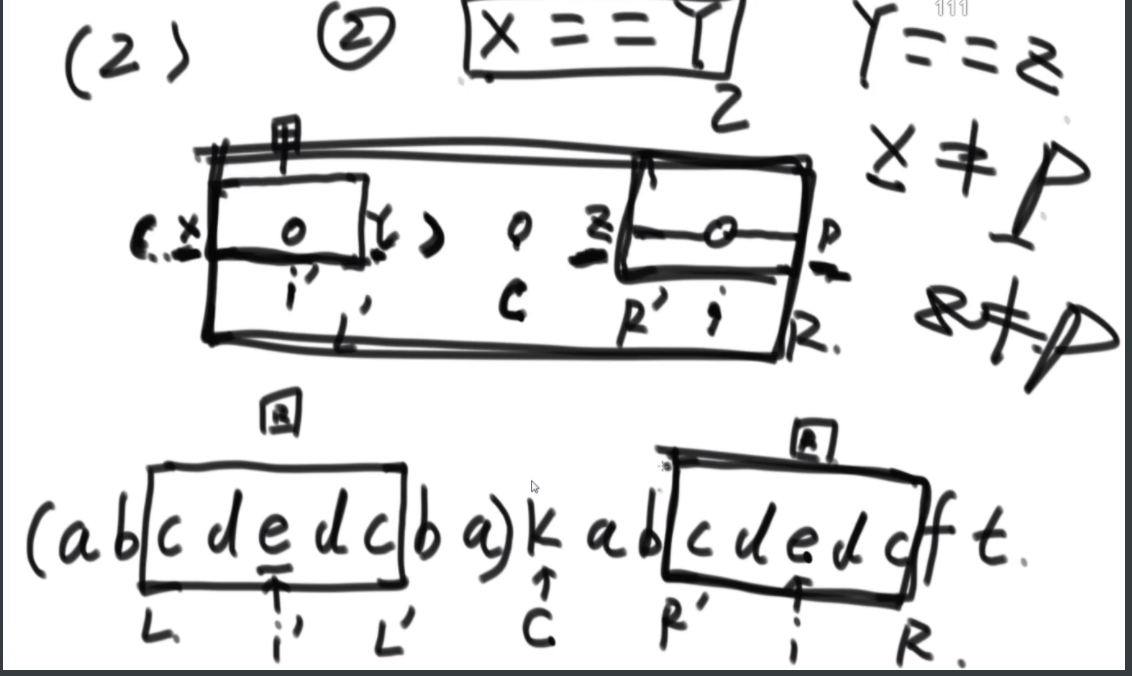
     证明：甲在i'回文串里面，因此甲和乙一定是回文，i的半径至少为i~R,又因为XYZ！=P，因此不可能再长了，因为如果X==P那么C的回文直径应该更长。

   • 2情况下的第三种情况，i'的回文区域在L处，正好压线。那么i的回文半径至少为i~R，能不能更远不知道，需要去 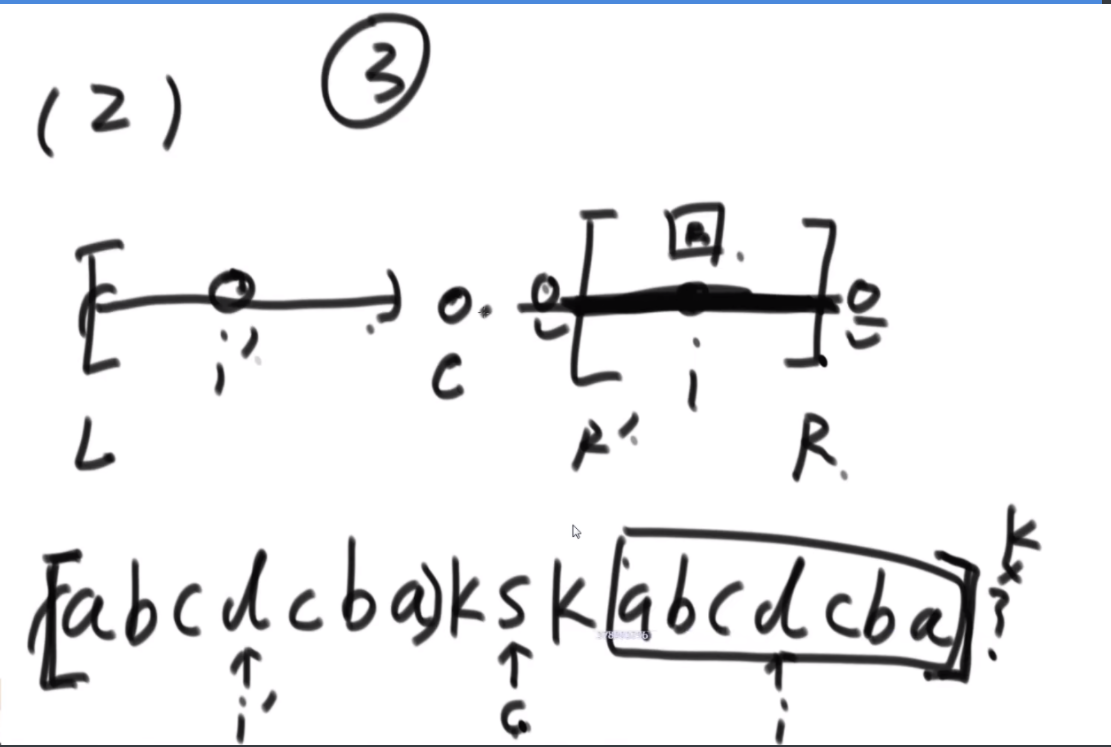尝试。

时间复杂度分析：第一四分支会让R变大，其余的时候R直接出结果，因此R是每个位置都会越来越大，因此时间复杂度O(N)

代码：

package ZuoShen.Class10;

public class Manacher {
    // 1221 -> #1#2#2#1#
    public static char[] manacherString(String str) {
        char[] charArr = str.toCharArray();
        char[] res = new char[str.length() * 2 + 1];
        int index = 0;
        for (int i = 0; i != res.length; i++) {
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }

    public static int maxLcpsLength(String str) {
        if (str == null || str.length() == 0) {
            return 0;
        }
        char[] charArr = manacherString(str); // 1221 -> #1#2#2#1#
        int[] pArr = new int[charArr.length]; // 回文半径数组
        int C = -1; //中心
        int R = -1; //回文右边界的再往右一个位置，最右的有效区是R-1位置
        int max = Integer.MIN_VALUE; //扩出来的最大值  即结果
        for (int i = 0; i != charArr.length; i++) { //每一个位置都求回文半径
            // i至少的回文区域，先给pArr[i]   min(  i'的半径，R-i)
            pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
            //右边要验的位置和左边要验的位置不越界
            while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                //至少不用验的区域跳过后，前后的是否一样 （扩）
                if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
                    //知道第二种情况的第1、2种小情况扩一次就会失败  因此没怎么浪费
                    pArr[i]++;
                else {
                    break;
                }
            }
            if (i + pArr[i] > R) {
                R = i + pArr[i];
                C = i;
            }
            max = Math.max(max, pArr[i]);
        }
        return max - 1; //处理出来的带'#'字符的半径长度为原串长度+1
    }
    public static void main(String[] args) {
        String str1 = "abc1234321ab";
        System.out.println(maxLcpsLength(str1));
    }
}

滑动窗口

由一个代表题目，引出一种结构
【题目】
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边，窗口每次 向右边滑一个位置。
例如，数组为[4,3,5,4,3,3,6,7]，窗口大小为3时:
[4 3 5]4 3 3 6 7
4[3 5 4]3 3 6 7
4 3[5 4 3]3 6 7
4 3 5[4 3 3]6 7
4 3 5 4[3 3 6]7
4 3 5 4 3[3 6 7]
窗口中最大值为5 窗口中最大值为5 窗口中最大值为5 窗口中最大值为4 窗口中最大值为6 窗口中最大值为7
如果数组长度为n，窗口大小为w，则一共产生n-w+1个窗口的最大值。
请实现一个函数。 输入:整型数组arr，窗口大小为w。
输出:一个长度为n-w+1的数组res，res[i]表示每一种窗口状态下的 以本题为例，结果应该返回{5,5,5,4,6,7}。

窗口只能右边界或左边界向右滑的情况下，维持窗口内部最大值或者最小值快速更新的结构
窗口内最大值与最小值更新结构的原理与实现：

首先是最大值：窗口选择双端队列实现，两端都可以进出，维持住大小从左往右是从大到小。里面存的不是数据，而是对应数组的脚标，窗口有两端，L和R。当R往右走时，将跨过的元素去和队列中最右侧的比较，如果跨过的元素比取出的元素大，那么丢掉取出的元素，再取，直到取出一个比跨过元素大的元素，将跨过的元素追加到这个元素后面，得以维持从大到小的顺序，或者如果队列里面的都比跨过的小，那么就全部取出，全部丢掉，将跨过的元素放进去。当L往右走时，跨过的元素即失效的元素，如果失效的元素的脚标是队列头部（即目前窗口内最大的元素），在队列中取出它并丢掉，如果不是，无事发生。

双端队列中记录的信息是：如果此时不让R再动，而选择依次让L动的话，谁会依次成为最大值这个优先级信息。所以为什么R跨过的元素进入时可以直接丢掉比它小的元素呢，因为这个元素同在窗口中，比那些被丢掉的元素晚过期，而且被丢掉的那些再也不可能在这个窗口中成为最大值了。时间复杂度总的是O(n)，单次的平均是O(1)。

package ZuoShen2.Class04;

import java.util.LinkedList;

public class SlidingWindowMaxArray {
    // w是窗口的大小
    public static int[] getMaxWindow(int[] arr, int w) {
        if (arr == null || w < 1 || arr.length < w) {
            return null;
        }
        // 存的是脚标 值  大->小
        LinkedList<Integer> qmax = new LinkedList<Integer>();
        int[] res = new int[arr.length - w + 1];
        int index = 0;
        for (int i = 0; i < arr.length; i++) { //窗口（刚才讲的）的R
            //i -> arr[i]
            while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[i]) {
                qmax.pollLast();
            }
            qmax.addLast(i);
            if (qmax.peekFirst() == i - w) { //i-w 过期的脚标
                qmax.pollFirst();
            }
            if (i >= w - 1) { //窗口形成了
                res[index++] = arr[qmax.peekFirst()];
            }
        }
        return res;
    }
    // for test
    public static void printArray(int[] arr) {
        for (int i = 0; i != arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] arr = { 4, 3, 5, 4, 3, 3, 6, 7 };
        int w = 3;
        printArray(getMaxWindow(arr, w));

    }
}

单调栈

在数组中想找到一个数，左边和右边比这个数小、且离这个数最近的位置。
如果对每一个数都想求这样的信息，能不能整体代价达到O(N)？需要使用到单调栈结构
单调栈结构的原理和实现:

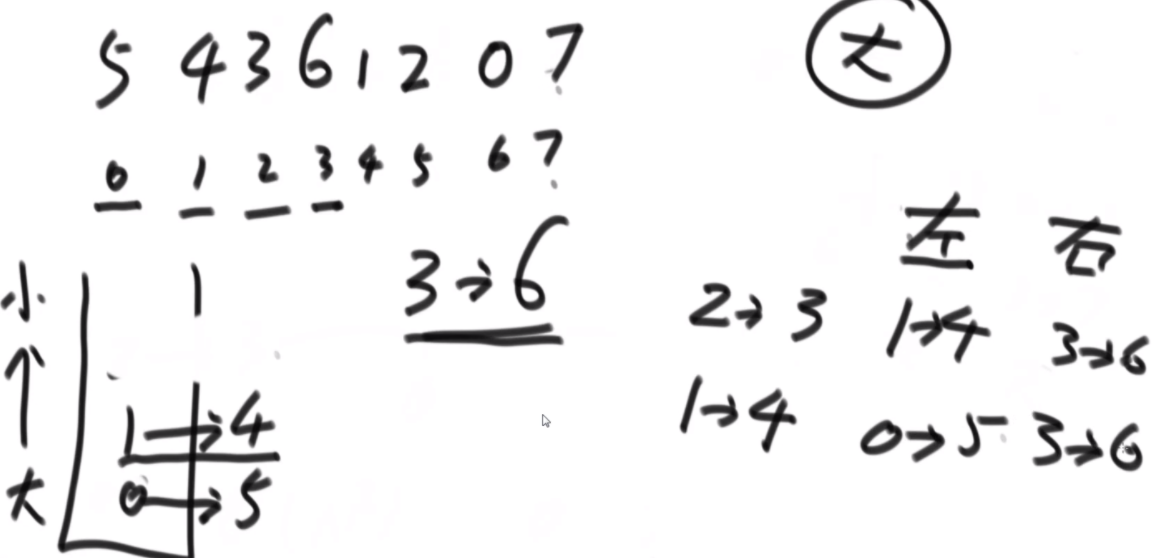
左下角处为栈，要维持它从栈低到栈顶单调性为从大到小，并且保存的是数组的脚标，依次往里面压入，5、4、3因为保持了单调性所以可以直接放进去，当6进入的时候，为了保持单调性，比6小的要弹出，弹出的元素，右边比它大的最近的元素是6（即使它弹出的元素），左边比它大的最近的元素是栈的现在的栈顶。（这种情况是无重复元素的情况）

有重复元素的情况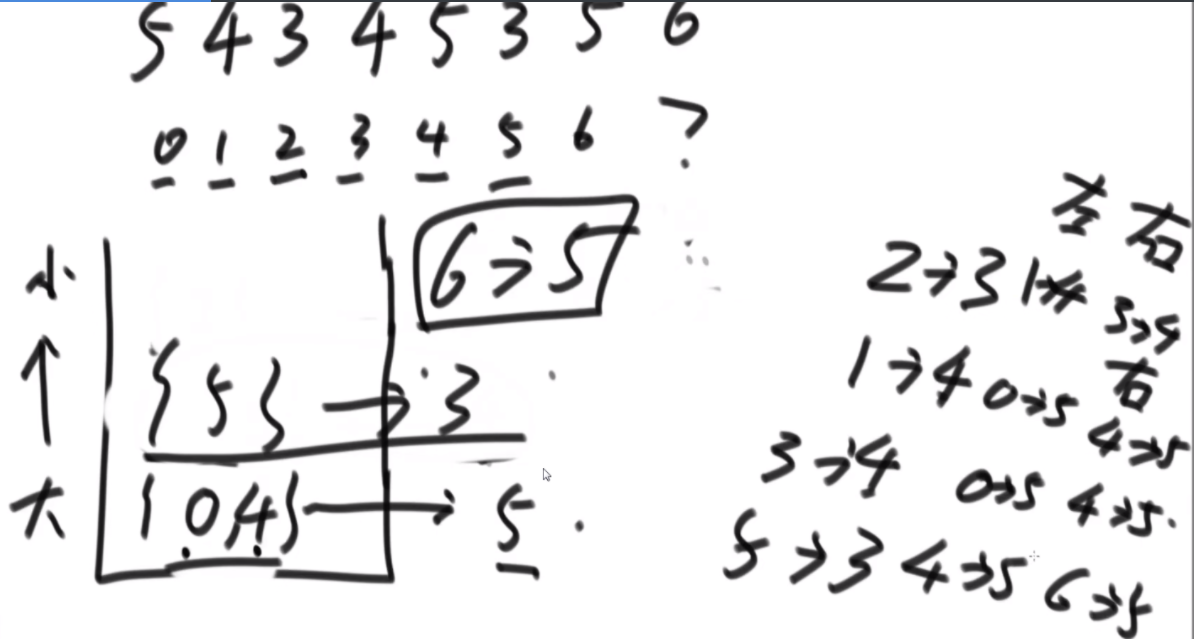， 这种时候，把相同的值下标压到一起，在同一个链表里，弹出的时候，右边离他最近比它大的还是使他弹出来的元素，左边是它下面链表的最后一个元素。

题目：

定义：数组中累加和与最小值的乘积，假设叫做指标A。
给定一个数组，请返回子数组中，指标A最大的值。

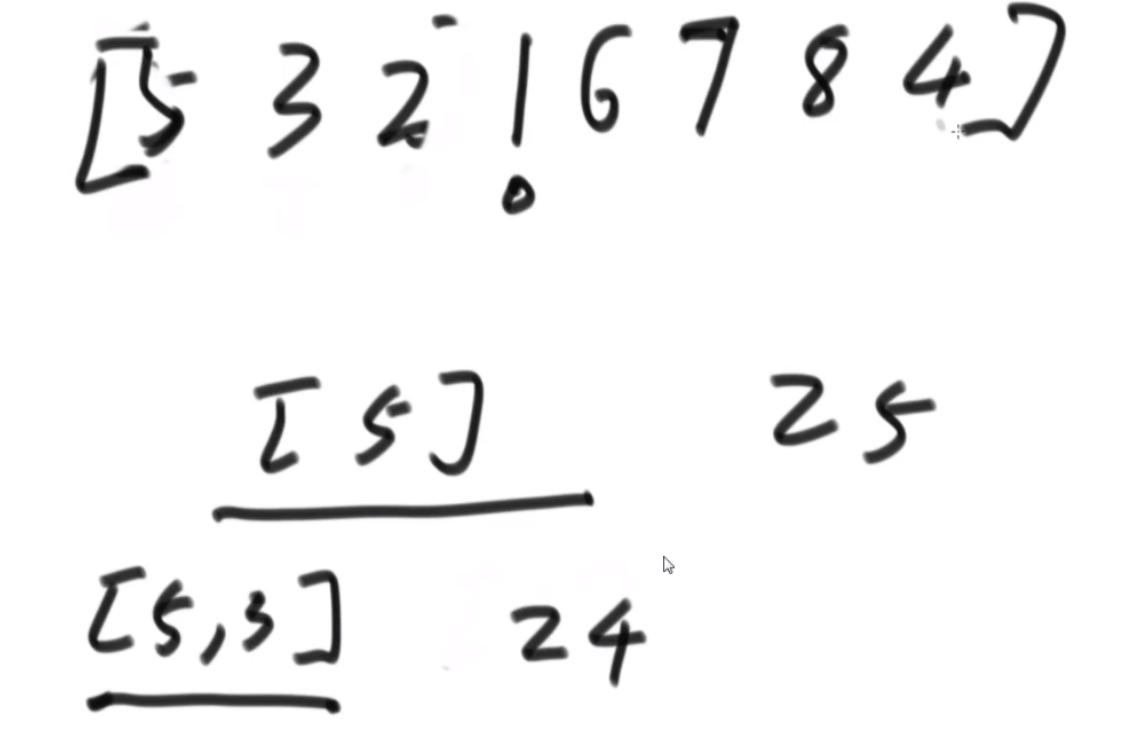
去找每个位置上的以这个位置为最小值的子数组，每个位置上可能有多个子数组，比如3位置上，子数组可以为[5,3]和[3]，他们中累加和乘上3最大的留下（这里因为最小值固定了，因此可以通过单调栈来找到累加和最大的子数组），上面单调栈结构求的是左右两边比当前位置大的，现在是找左右两边比它小的。

p12:

岛问题

【题目】
一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右 四个位置相连，如果有一片1连在一起，这个部分叫做一个岛，求一个矩阵中有多少个岛?
【举例】
001010
111010
100100
000000
这个矩阵中有三个岛
【进阶】
如何设计一个并行算法解决这个问题

思路：从左上角往右遍历矩阵，找到1就去进行一个infect（感染）过程，把这一个岛上的1感染成2，infect一次就岛数+1，然后一次遍历 结束。

package ZuoShen.Class10;

public class Islands {
    //时间复杂度 O(N*M) 整体的时候 一次  infect时候，最多4次
    public static int countIslands(int[][] m) {
        if (m == null || m[0] == null) {
            return 0;
        }
        int N = m.length;//行
        int M = m[0].length;//列
        int res = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (m[i][j] == 1) {
                    res++;
                    infect(m, i, j, N, M);
                }
            }
        }
        return res;
    }

    public static void infect(int[][] m, int i, int j, int N, int M) {
        //base case  i,j越界
        if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {
            return;
        }
        //i,j没越界，并且当前位置值是1
        m[i][j] = 2;
        //上下左右四个方向都去传染
        infect(m, i + 1, j, N, M);
        infect(m, i - 1, j, N, M);
        infect(m, i, j + 1, N, M);
        infect(m, i, j - 1, N, M);
    }

    public static void main(String[] args) {
        int[][] m1 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 1, 1, 1, 0, 1, 1, 1, 0 },
                { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                { 0, 1, 1, 0, 0, 0, 0, 0, 0 },
                { 0, 0, 0, 0, 0, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m1));

        int[][] m2 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 1, 1, 1, 1, 1, 1, 1, 0 },
                { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                { 0, 1, 1, 0, 0, 0, 1, 1, 0 },
                { 0, 0, 0, 0, 0, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m2));

    }

}

进阶：如何通过一个并行算法解决这个问题？ 一般问并行只需要说明思路，而且虽然单行O(N*M)但是数据量太大还是得并行。

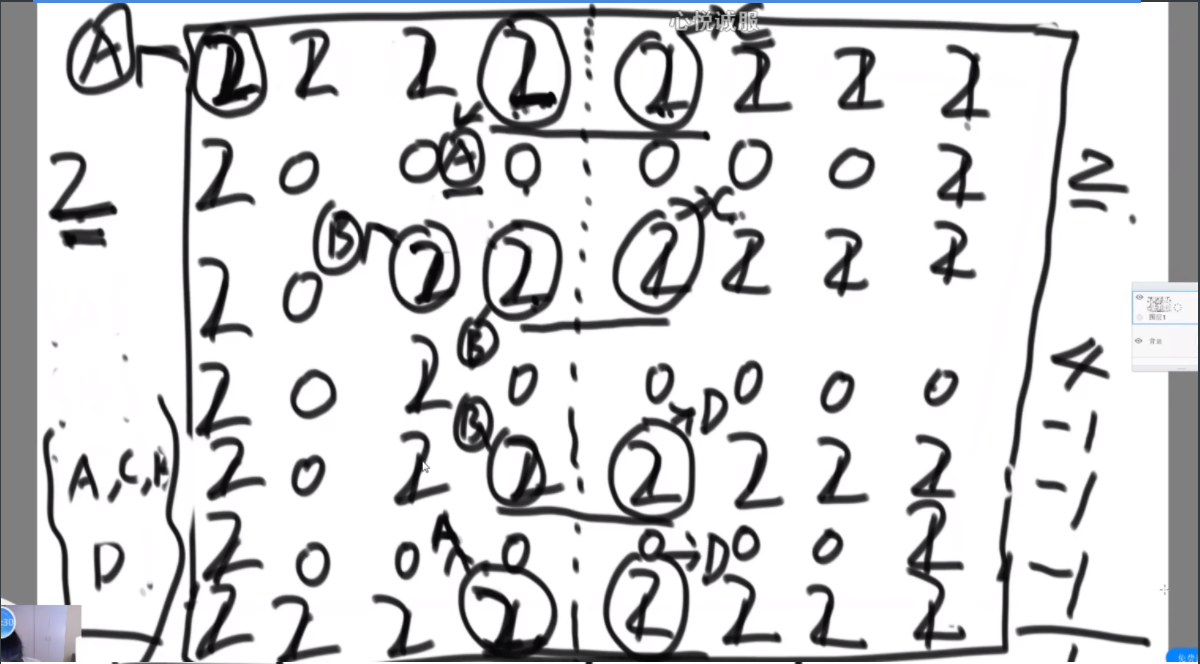
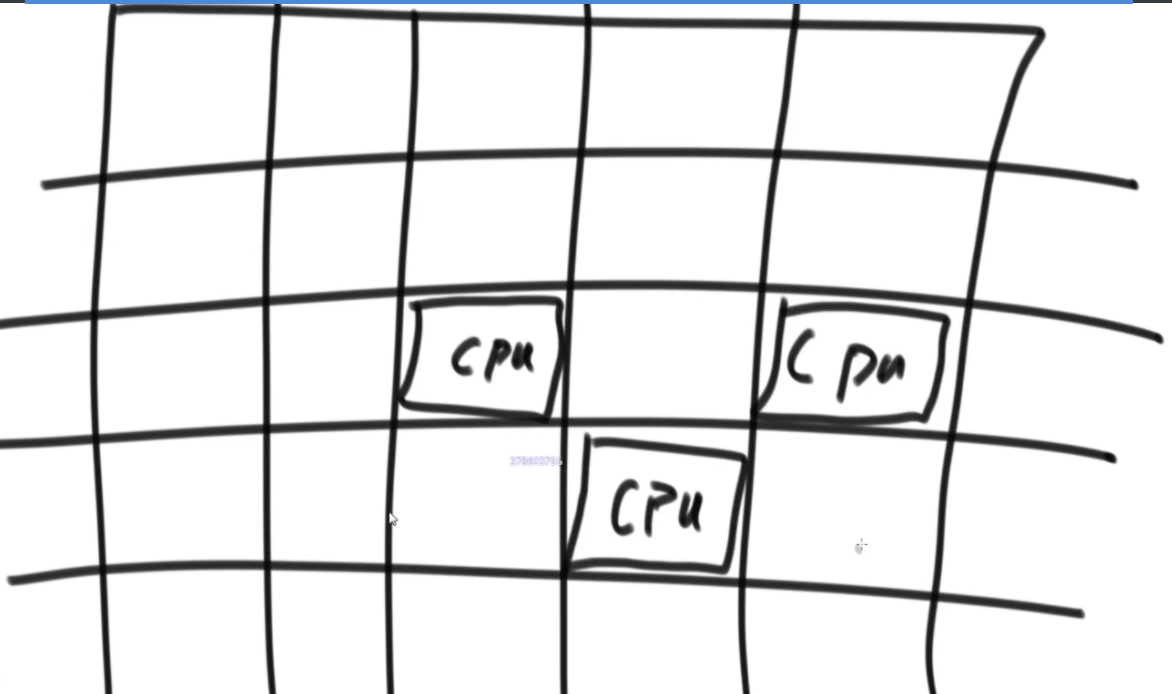
两个CPU并行，将岛从中间分成两半，然后各自看不见对方的，因此每半片区域都有俩岛，共有4个，然后记录岛为节点{A},{B},{C},{D}，完事后在边界处相遇的点如果不同属于一个集合，那么合并，岛数-1，直至没有相遇的点。

如果是多个CPU，那么每个CPU计算自己的岛数后，保存4个边界的记录，再进行合并。

MapReduce的精巧版本，map就是并行计算，reduce就是返回合并。

并查集

需求：{a},{b},{c},{d},{e},现在的功能需求是boolen:issameset（a,b），和void union(a,b)，第一个是判断是否是属于同一个集合，第二个是把两个元素的集合合并。如果使用链表，那么合并很快，但是判断是否相同很麻烦，如果使用hashset，判断是否相同很快，但是合并也不是O(1)，因此需要并查集。

思路：每个元素指向自己先，然后判断是否属于同一个集合，就看往上走走到头走不了的元素是否相同即可，合并的时候就把集合size小的集合的最上面直接指向size较大的那个集合的最上面的节点。

优化：当判断是否是同一集合的过程中，会不断往上找，在找完之后，将沿途的父节点指向直接修改成指向根节点。

并查集时间复杂度是随着getHead函数调用次数逼近O(N)时，单次代价可以认为是O(1)的。

并查集代码

package ZuoShen.Class10;

import java.util.HashMap;
import java.util.List;
import java.util.Stack;

public class UnionFind {
    public static class Element<V> {
        public V value;

        public Element(V value) {
            this.value = value;
        }

    }

    public static class UnionFindSet<V> {
        //给一个V  得一一对应加工出来的元素
        public HashMap<V, Element<V>> elementMap;

        //key代表一个节点  value代表它的父节点
        public HashMap<Element<V>, Element<V>> fatherMap;

        //key代表这个小集合的根节点（代表结点）  value代表它的size
        public HashMap<Element<V>, Integer> rankMap;

        public UnionFindSet(List<V> list) {
            elementMap = new HashMap<>();
            fatherMap = new HashMap<>();
            rankMap = new HashMap<>();
            for (V value : list) {
                Element<V> element = new Element<V>(value);
                elementMap.put(value, element);
                fatherMap.put(element, element);
                rankMap.put(element, 1);
            }
        }

        private Element<V> findHead(Element<V> element) {
            Stack<Element<V>> path = new Stack<>();
            while (element != fatherMap.get(element)) {
                path.push(element);
                element = fatherMap.get(element);
            }
            while (!path.isEmpty()) {
                fatherMap.put(path.pop(), element);
            }
            return element;
        }

        public boolean isSameSet(V a, V b) {
            //并查集使用的前提是有初始化
            if (elementMap.containsKey(a) && elementMap.containsKey(b)) {
                return findHead(elementMap.get(a)) == findHead(elementMap.get(b));
            }
            return false;
        }

        public void union(V a, V b) {
            if (elementMap.containsKey(a) && elementMap.containsKey(b)) {
                Element<V> aF = findHead(elementMap.get(a));
                Element<V> bF = findHead(elementMap.get(b));
                if (aF != bF) {
                    Element<V> big = rankMap.get(aF) >= rankMap.get(bF) ? aF : bF;
                    Element<V> small = big == aF ? bF : aF;
                    fatherMap.put(small, big);
                    rankMap.put(big, rankMap.get(aF) + rankMap.get(bF));
                    rankMap.remove(small);
                }
            }
        }

    }
}

KMP

KMP算法解决的问题：字符串str1和str2，str1是否包含str2，如果包含返回str2在str1中开始的位置。

如何做到时间复杂度O(N)完成？

暴力解法：遍历str1，如果第一个字符相同，往后走，依次判断，是否每个字符都和str2一致，时间复杂度最差为O(N*M)，N为str1长度，M为str2长度。

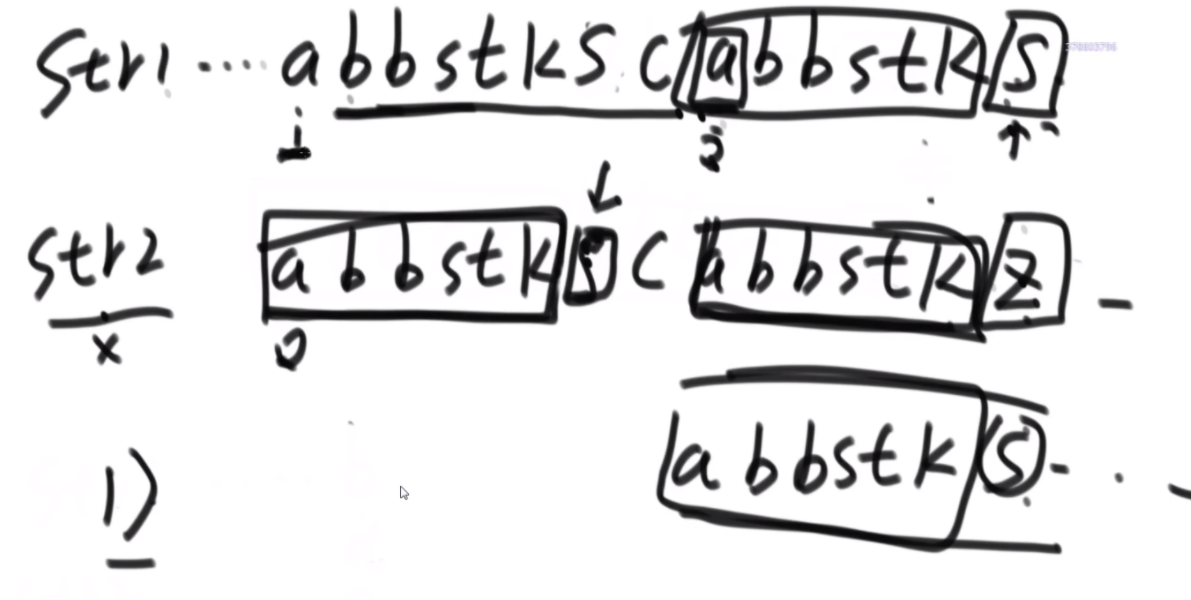
KMP：先对str2搞一个nextarr[]，里面放着的是每个元素往前数，前缀字符和后缀字符相等的最大长度，这个长度不能是全部。next[i] 表示 P[0] ~ P[i] 这一个子串，使得 前k个字符恰等于后k个字符 的最大的k. next是针对模式串也就是str2的

当str1在上图中，从i开始比较到第四个S的时候，发现前面和str2都一样结果这不一样。下次str1从j处开始比较，不过优化到箭头处开始比较，不过失败了的话还是从j+1开始走（首先是下图解释了为什么i~j中间不可能有结果，因为如果有结果的话说明前缀和后缀相等的最大长度有更大的值，这个结论不可能存在，因此可以直接跳到j开始，然后因为j到箭头处和str2开头到str2的箭头处也就是前缀内容一样，因此可以跳到箭头处去比较），str2从第一个K后面比较，即nextarr中Z字符在数组中存的值的下一个。

举例子：

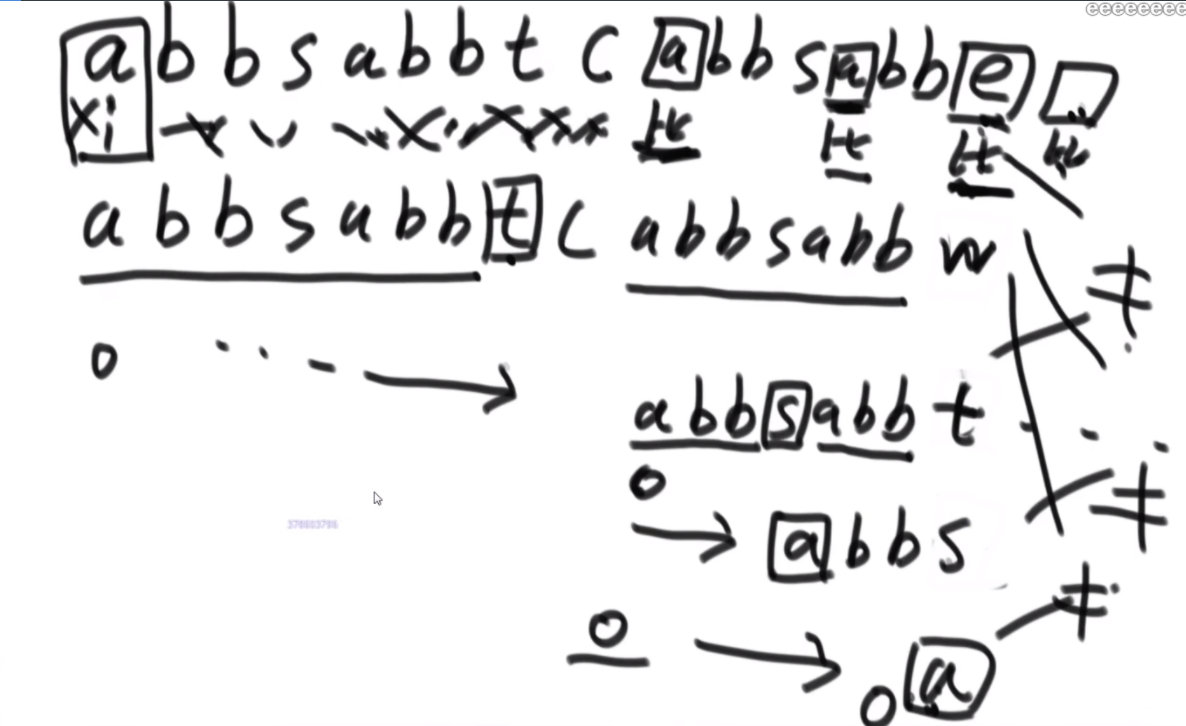
1. str1和str2从头比到最后发现e≠w，不一致。
2. 此时比对位置从i跳到了str1第二个框住的a（这里的位置是e往前走7个格子，也就是w对应的值），不过因为已知后缀和前缀相同，因此比较的元素还是e≠t(t是根据w的nextarr中的值7再+1找到的，也就是说str2的第二次比较是从第8个元素t开始的)。
3. t的nextarr中的值为3，因此str2下一次比对的值为第4个元素s，str1的比对位置从第二个框跳到了第三个框（这里的位置是e往前走3个格子，也就是t对应的值），不过比对的元素还是e，e≠s，不一致。
4. s的nextarr中的值为0，因此str2下一次比对的值为第1个元素a，str1的比对位置这次挪到了e（这里的位置是e往前走0个格子，也就是s对应的值），e≠a，不一致，str1的比较位置走向e的下一位，str2的比较位置不变。

代码思路：只需要str2的指针往前跳或者跳到0位置上str1的指针往后走，以及相等的时候str2往后走。只有三个判断分支。也就是str1不需要去管框住的位置。

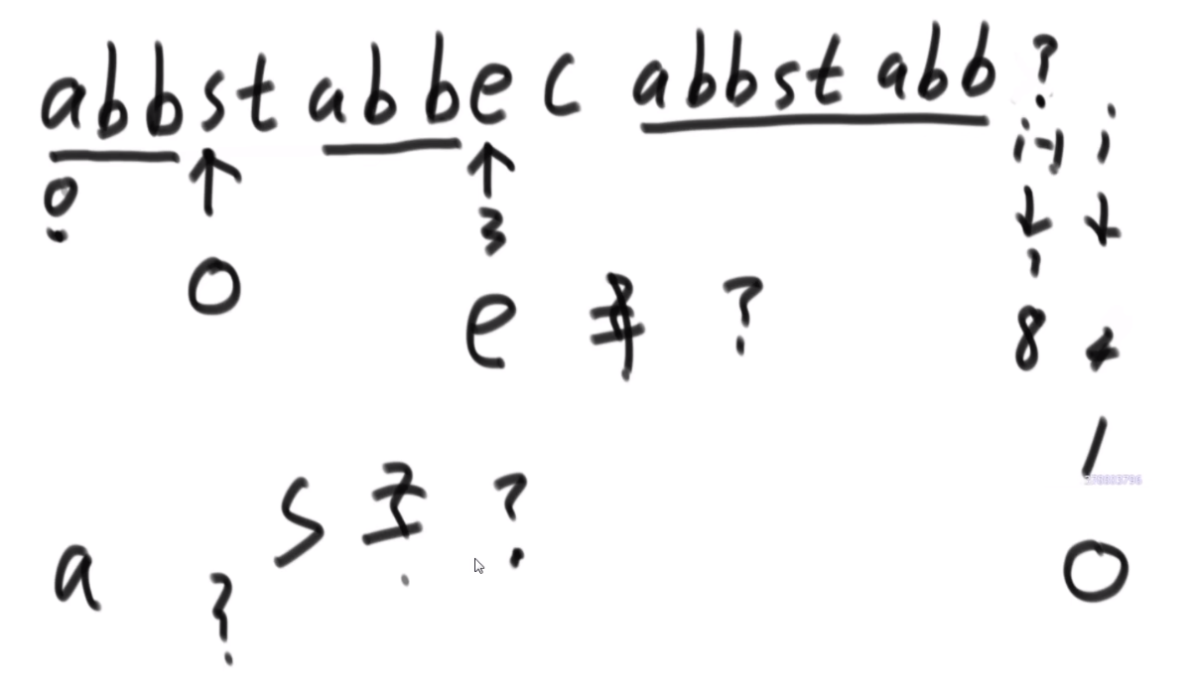
next数组的生成过程，i位置上的长度，看i-1的位置上的长度，上图为8，那么和8位置上的元素e比较，如果?e，则i上为9，否则再往前跳，跳到e的长度3上，?s，如果不等向前跳到0，？==a，再不等，为0。

KMP代码：

package ZuoShen.Class10;

public class KMP {
    // s.length() >= m.length()
    public static int getIndexOf(String s, String m) {
        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
            return -1;
        }
        char[] str1 = s.toCharArray();
        char[] str2 = m.toCharArray();
        int i1 = 0;
        int i2 = 0;
        int[] next = getNextArray(str2); // O(M)
        //O(N)  2N?
        //时间复杂度 i1 (N)  i1-i2(N) 去比较三个分支这两个值的变化  相加为2N
        while (i1 < str1.length && i2 < str2.length) {
            if (str1[i1] == str2[i2]) {
                i1++;
                i2++;
            } else if (next[i2] == -1) { //只有next中0位置上的元素为-1  等价于i2==0
                i1++;
            } else {
                //str2的索引还能往前跳
                i2 = next[i2];
            }
        }
        //i1越界或i2越界了 只要i2越界了 就说明找到了匹配的字符，返回i1-i2也就是字符串的起始位置
        return i2 == str2.length ? i1 - i2 : -1;
    }

    public static int[] getNextArray(char[] ms) {
        if (ms.length == 1) {
            return new int[] { -1 };
        }
        int[] next = new int[ms.length];
        next[0] = -1;
        next[1] = 0;
        int i = 2; //数组走到的位置
        int cn = 0;
        //时间复杂度 i (M)  i-cn(M) 去比较三个分支这两个值的变化  相加为2M
        while (i < next.length) {
            if (ms[i - 1] == ms[cn]) {
                //cn即代表和i-1比较的位置，也代表当前值
                //++cn，是因为相同了所以长度+1，并且给下一个位置cn保留正确值，i++，是因为这个位置比较完了去比较下一个位置
                next[i++] = ++cn;
            } else if (cn > 0) {
                //如果不相等，cn往前跳
                cn = next[cn];
            } else {
                next[i++] = 0;
            }
        }
        return next;
    }
    public static void main(String[] args) {
        String str = "abcabcababaccc";
        String match = "ababa";
        System.out.println(getIndexOf(str, match));

    }
}

p11:

认识哈希函数和哈希表的实现

哈希函数：

1. 输入域无穷（长度不限制的字符串） 输出域一定有穷尽 MD5：0~2⁶⁴-1 SHa1：0~2¹²⁸-1 java:0~2³²-1
2. 相同的输入，一定会返回相同的值（没有任何随机的成分）
3. 不同的输入，也会有时有相同的输出（哈希碰撞，这是必然会发生的情况）
4. 最重要的性质 离散均匀的散列那些点，防止点去聚集 离散性均匀性越好 这个哈希函数越好

统计出现次数最多的数

无符号整数 0~2³²-1 有40亿个数 假设给1G内存，如何计算出现次数最多的数？

传统方式：HashMap key(int)--4B value(int 次数)--4B 大概需要32G内存（最坏情况 每个数都不一样） 因此不行

思路：把这40亿个数输入哈希函数得到结果，再%100，根据结果放入0~99号文件中，这里内存没爆，每个文件大小0.32G。同时相同的数字一定在一个文件中，尽管这个文件中也有不同的数字，再分别统计这100个文件中各自出现次数最多的数字，再在100个中找到次数最大的那个，完成任务。

哈希表的实现

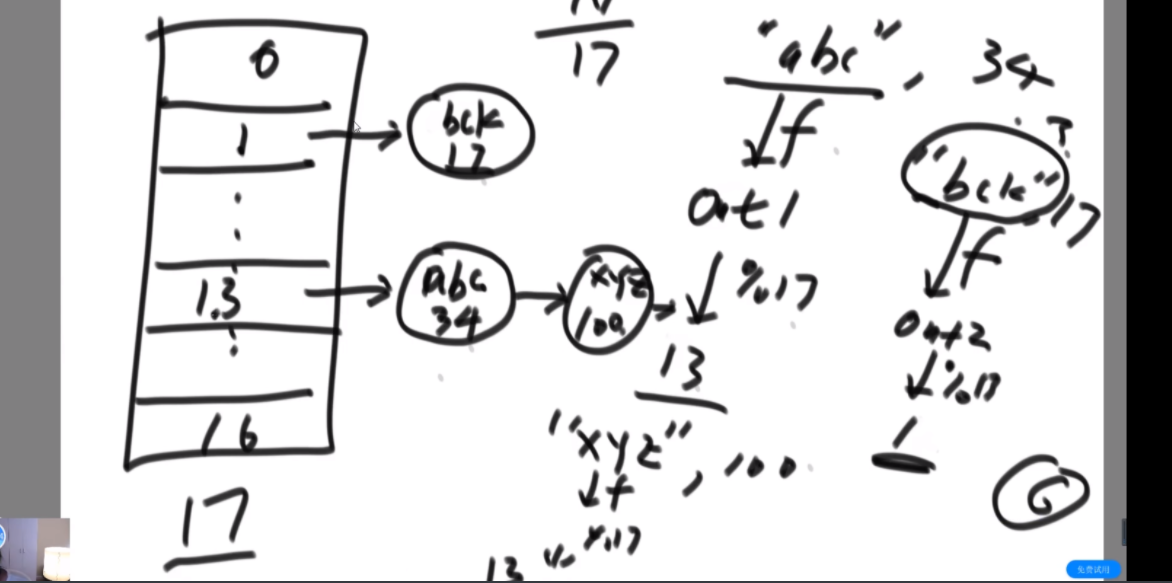
先是有0-17大小的数组，假设（“abc”,34）哈希函数结果再%17得到13，就添加到数组13位置上的链表处，依次添加。

当一个链表长度到了6时，（其他的链表因为均匀性差不多也到6了）触发扩容机制，将17个大小的数组换成34大小的数组，并且重新计算哈希值，不过这次是%34了。

扩容次数:O(logN)，每次的代价O(N），N为元素数量，因此总的代价为O(N*logN)。这个logN是假设每个链只放两个元素，因此底是2，如果把链放的长一点，虽然查询代价提升，但是可以大幅度降低logN的大小。

因为Java中的JVM（虚拟机语言中有,C这种没有）可以有离线扩容机制（在用户的链表长度有点长的时候，不占用用户时间去新建一个扩容后大小的哈希表，然后建好后再直接引过来），因此省去了扩容的时间，增删改查可以视作O(1)，所以哈希表是使用上可以看做O(1)，而理论上（O(logN)）不能。

设计RandomPool结构

【题目】
设计一种结构，在该结构中有如下三个功能:
insert(key):将某个key加入到该结构，做到不重复加入
delete(key):将原本在结构中的某个key移除
getRandom(): 等概率随机返回结构中的任何一个key。
【要求】
Insert、delete和getRandom方法的时间复杂度都是O(1)

思路：搞两个hashmap，map1是以放入的值作为key,value是逐渐递增的标号，记录这个key是第几个加入的。map2与map1正好相反，key是标号，value是值。这样可以做到用map2实现Random查询，但是删除的时候标号会乱，只要将最后一个元素拿出来覆盖到被删掉的那个元素，这样标号就会一直连续的。

package ZuoShen.Class10;

import java.util.HashMap;

public class RandomPool {
    public static class Pool<K> {
        private HashMap<K, Integer> keyIndexMap;
        private HashMap<Integer, K> indexKeyMap;
        private int size;

        public Pool() {
            this.keyIndexMap = new HashMap<K, Integer>();
            this.indexKeyMap = new HashMap<Integer, K>();
            this.size = 0;
        }

        public void insert(K key) {
            if (!this.keyIndexMap.containsKey(key)) {
                this.keyIndexMap.put(key, this.size);
                this.indexKeyMap.put(this.size++, key);
            }
        }

        public void delete(K key) {
            if (this.keyIndexMap.containsKey(key)) {
                int deleteIndex = this.keyIndexMap.get(key);
                int lastIndex = --this.size;
                K lastKey = this.indexKeyMap.get(lastIndex);
                this.keyIndexMap.put(lastKey, deleteIndex);
                this.indexKeyMap.put(deleteIndex, lastKey);
                this.keyIndexMap.remove(key);
                this.indexKeyMap.remove(lastIndex);
            }
        }

        public K getRandom() {
            if (this.size == 0) {
                return null;
            }
            int randomIndex = (int) (Math.random() * this.size); // 0 ~ size -1
            return this.indexKeyMap.get(randomIndex);
        }

    }

    public static void main(String[] args) {
        Pool<String> pool = new Pool<String>();
        pool.insert("zuo");
        pool.insert("cheng");
        pool.insert("yun");
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());

    }
}

详解布隆过滤器 Bitmap

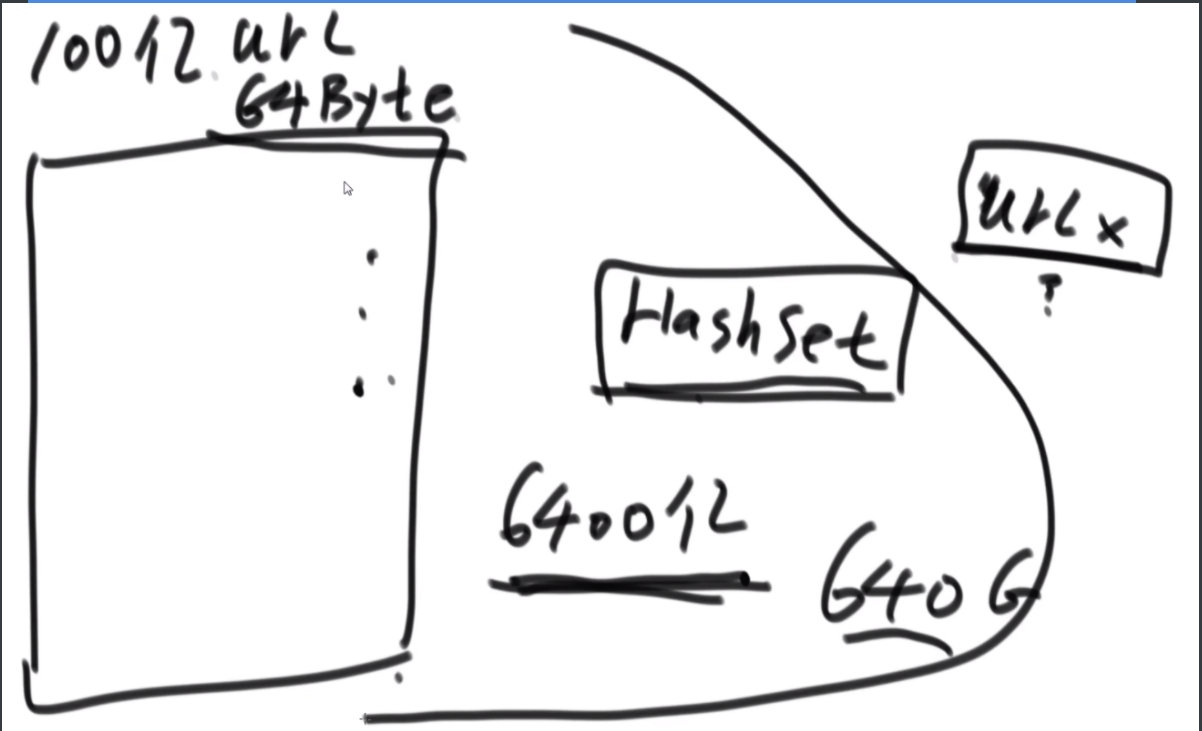
有个公司，有100亿个url，这些url是浏览器中禁止访问的，且不用删除，因此只有添加和查询两个操作。假设一个url64Byte，那么假如用内存的话需要640G，太大了。

同理：爬虫开了1000个线程，通过深度优先或者广度优先去爬网址，当然希望这些线程之间爬取的url不要重复，因此在要爬一个url的时候先问问爬过没，因此同样的需求。

要求只有增加和访问，没有删除。并且会有一定的失误率（不可避免），布隆过滤器只有一种失误（白名单当成了黑名单，或者是没爬过的当成了爬过的，理解为被错杀了），并且概率可以做到很低。

int[] 100 0~99 每个4字节，32bit,相当于1字节8位；long[] 100 0~99 每个8字节，64bit；bit[] 100 0~99 每个1bit。

思路：每一个url 通过k个哈希函数计算出k个结果，再%m，得到k个脚标，全部涂成1 这样再来url就也走这个路，如果全为1说明存过这个url，否则有一个0就说明没存过。 先决定m，再决定k以及哈希函数。

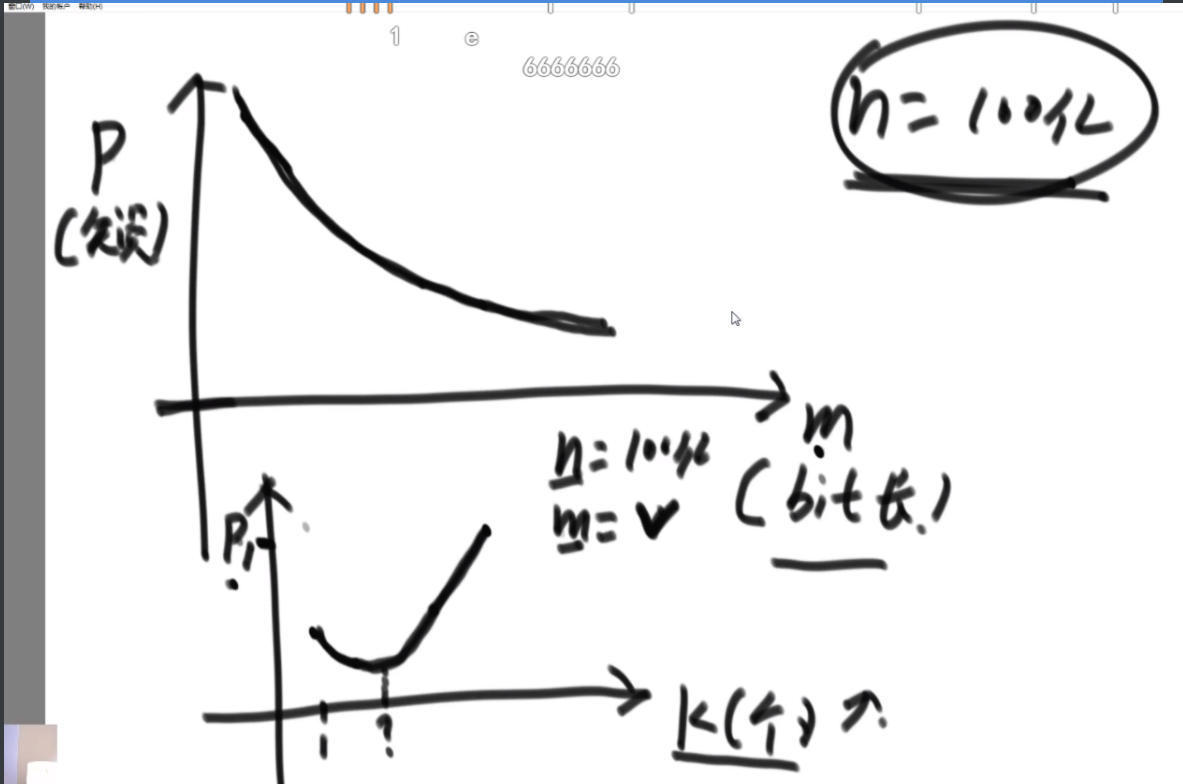
失误率和n决定m，m和n和p决定K。n=样本量，p=失误率。

1. 判断是不是类似于黑名单，允许失误率。
2. 问样本量和失误率允许多少，和单样本大小无关。

m=-(n*lnp)/(ln2)² 向上取整 p假如是0.0001 只需要26G

k=ln2m/2 ≈ 0.7m/n (个) 向上取整

完事后问一问能不能给更多空间，如果给了30G的空间，那么可以算出来真实的失误率 p真=（1-e^-n*k真/m真）^k真 真实失误率是十万分之六，小于万分之一。

bitmap原理

package ZuoShen.Class10;

public class BitMap {
    public static void main(String[] args) {
        int a = 0;
        //a 32 bit
        int[] arr = new int[10]; //32bit * 10 -> 320bits
        //arr[0]  int 0~31 bit   11111111 11111111 11111111 11111111
        //arr[1]  int 32~63 bit
        //arr[2]  int 64~95 bit
        int i = 178;  //想取得178个bit的状态
        int numIndex = 178/32;//代表第178位应该在哪个int数上去找
        int bitIndex = 178%32;//代表在这个数上的第多少位  假设是第3位  就是从右往左数
                              //低位的 所以右移
        //拿到178位的状态  1的位表示：  00000001 因此与完后 得到的是最右侧的位的状态
        int s = ((arr[numIndex] >> (bitIndex) ) & 1);

        //把178位的状态改为1   00000001 左移3位  00001000 再或 因此可以修改为1
        arr[numIndex] = arr[numIndex] | (1 << (bitIndex));

        //把178位的状态改为0   00000001 左移3位  00001000 取反 11110111 取与运算 修改为0
        arr[numIndex] = arr[numIndex] & (~ (1 << (bitIndex)));
    }
}

详解一致性哈希原理

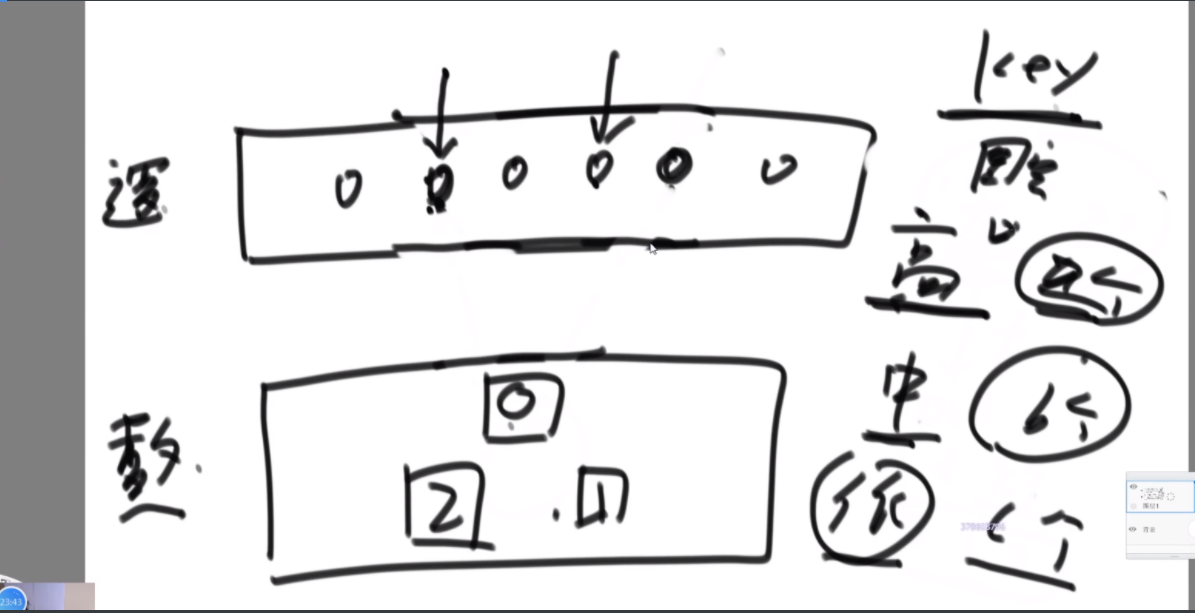
在分布式中，上面是逻辑层面的很多个服务器，每一个的逻辑是一样的。下面是数据库层面，假设里面有3个服务器0、1、2，一个数据要存过来，可以让它的key去走一个哈希函数，出来再%3，走到了3个数据服务器中的一个。因此选择合理的key是门学问，如果以国家的话，可能中美是最多的，然后两台数据服务器就很满，有一个没啥用，这中负载不均衡，因此不合理。性别的话，直接有一台就废了，两台爆满。

这种有问题，如果数据服务器增加或者减少的代价是所有数据重新计算哈希值，代价是全量的。这也是mysql一般只用一个很好的服务器去跑，而不去弄很多服务器的原因。

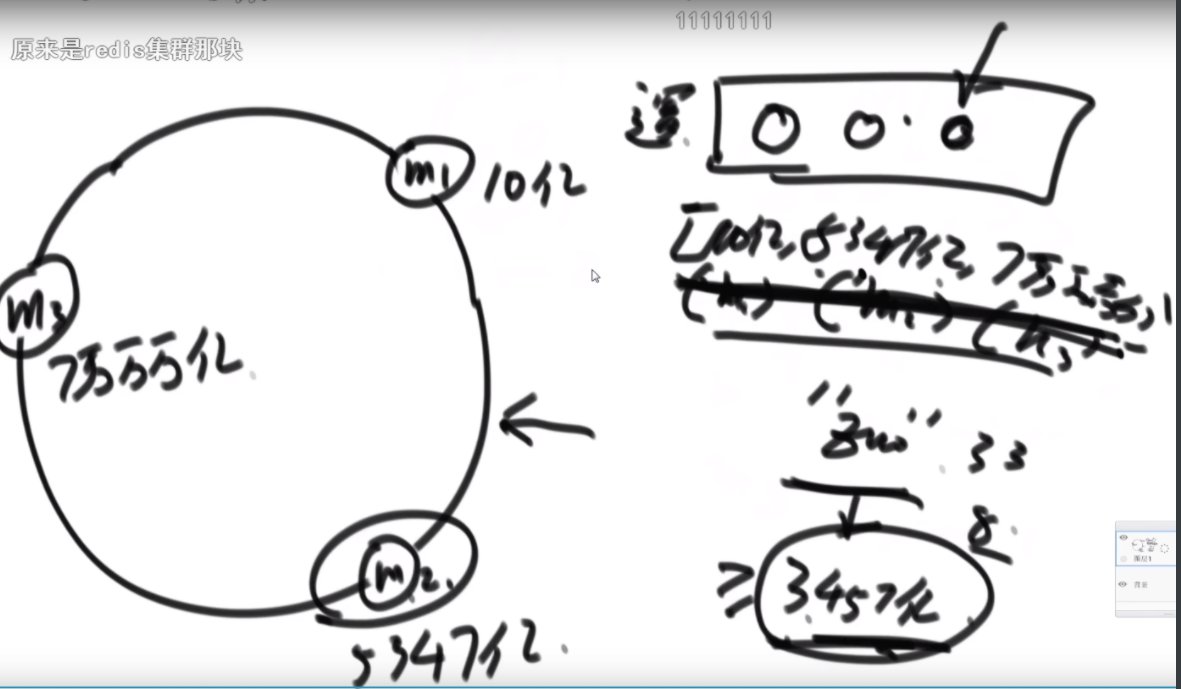
优化方式，将3台数据服务器以它们特有的名字去算一个md5的值，将md5的结果值看成一个环，新进来的内容如何判断存在了哪个数据服务器呢？就看在哪个线段上，m1至m2的归m2管，m2-m3的归m3管，以此类推，即顺时针离它哈希值最近的一台。如果新加入一个或者删除一个，那么只需要更新一小段的数据的索引。

这种也有问题：

1. 当数据服务器数量不够的时候，可能不能给环达到负载均衡。
2. 即使数量少的时候正好等分，但是新增的时候又会变成不均衡的状态。

这两个问题解决就可以完美使用一致性哈希。这个技术是虚拟节点技术。

m1、m2、m3各自生成1000个节点，均匀放在这个环上，各自抢各自的区域，新增节点就继续生成一千个节点均匀分布，问题解决。而且可以根据服务器能力情况去调整负载，m1强就生成2000个节点，m3弱就生成500个节点。大公司分布式都是这么做的，这篇论文是号称谷歌改变世界的三驾马车之一。

p10：

暴力递归

暴力递归就是尝试
1，把问题转化为规模缩小了的同类问题的子问题
2，有明确的不需要继续进行递归的条件(base case)
3，有当得到了子问题的结果之后的决策过程
4，不记录每一个子问题的解
一定要学会怎么去尝试，因为这是动态规划的基础，这一内容我们将在提升班讲述

汉诺塔问题

打印n层汉诺塔从最左边移动到最右边的全部过程

从最下面的base case看问题，如果它能满足小的盘在大的上面，那就都可以。

我们在利用计算机求汉诺塔问题时，必不可少的一步是对整个实现求解进行算法分析。到目前为止，求解汉诺塔问题最简单的算法还是同过递归来求。

步数：2^N-1次，N是圆盘个数。

实现这个算法可以简单分为三个步骤：

　　　　（1） 把n-1个盘子由A 移到 B；

　　　　（2） 把第n个盘子由 A移到 C；

　　　　（3） 把n-1个盘子由B 移到 C；

汉诺塔的base case是一个环的时候，因此i是从n逐渐-1递归。

package ZuoShen.Class09;

public class Hanoi {
    //A是起点   B是中介  C是终点
    public static void hanoi(int n, char A, char B, char C) {
        if (n == 1) {
            move(A, C);
        } else {
            hanoi(n - 1, A, C, B);//将n-1个盘子由A经过C移动到B
            move(A, C);             //执行最大盘子n移动
            hanoi(n - 1, B, A, C);//剩下的n-1盘子，由B经过A移动到C
        }
    }
    private static void move(char A, char C) {//执行最大盘子n的从A-C的移动
        System.out.println("move:" + A + "--->" + C);
    }
    public static void main(String[] args) {
        System.out.println("移动汉诺塔的步骤：");
        hanoi(3, 'a', 'b', 'c');
    }
}

打印一个字符串的全部子序列

思路：就像是一棵树，从第一个节点开始走，每条边可以选择要或者不要，要a，走左边，再要b，在走左边，不要c，走右边，所以就是ab，它的左边就是abc，以此类推。在代码上通过递归实现。

子序列的base case是它走完这个字符串长度的时候，因此是逐渐+1进行的递归。

package ZuoShen.Class09;

import java.util.ArrayList;
import java.util.List;

public class PrintAllSubsquence {
    public static void printAllSubsquence(String str) {
        char[] chs = str.toCharArray();
        process(chs, 0);
    }
    //省空间的版本
    public static void process(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
            return;
        }
        process(chs, i + 1);//要当前字符的路
        char tmp = chs[i];//利用系统的栈去记录tmp临时变量
        chs[i] = 0;
        process(chs, i + 1);//不要当前字符的路，因为第i个也就是当前字符被覆盖为0了
        chs[i] = tmp;//这一步还原当前字符，就是回溯，回溯：将条件修改为递归的样子
    }

    public static void function(String str) {
        char[] chs = str.toCharArray();
        process(chs, 0, new ArrayList<Character>());
    }
    //好理解 但是额外空间占用较多的版本
    //i代表从这个树的根往下走的层数，  当前来到i位置，要和不要，走两条路
    //res代表之前的选择所形成的列表
    public static void process(char[] chs, int i, List<Character> res) {
        if(i == chs.length) {
            printList(res);
        }
        List<Character> resKeep = copyList(res);
        resKeep.add(chs[i]);
        process(chs, i+1, resKeep); //要当前字符的路  因为add了当前字符
        List<Character> resNoInclude = copyList(res);
        process(chs, i+1, resNoInclude);//不要当前字符的路
    }
    public static void printList(List<Character> res) {
        // ...;
    }
    public static List<Character> copyList(List<Character> list){
        return null;
    }
    public static void main(String[] args) {
        String test = "abc";
        printAllSubsquence(test);
    }

}

打印一个字符串的全部排列

假设是abc，先选择a(bc)，然后b-c,c-b，然后再选择b(ac),然后a-c,c-a，c也同理。

这里因为是需要满足长度足够后才会输出，因此也是i+1进行递归，递归完成后依旧需要回溯。

package ZuoShen.Class09;

import java.util.ArrayList;

public class PrintAllPermutations {
    public static ArrayList<String> Permutation(String str) {
        ArrayList<String> res = new ArrayList<>();
        if (str == null || str.length() == 0) {
            return res;
        }
        char[] chs = str.toCharArray();
        process(chs, 0, res);
        res.sort(null);
        return res;
    }
    //chs[i..]范围上，所有的字符，都可以在i位置上，后续都去尝试  类比于a(bc),可以b在第二个，也可以是c
    //chs[0..i-1]范围上，是之前做的选择
    //请把所有的字符串形成的全排列，加入到res里去
    public static void process(char[] chs, int i, ArrayList<String> res) {
        if (i == chs.length) {
            res.add(String.valueOf(chs));
        }
        boolean[] visit = new boolean[26];//代表某一个字符是否尝试过
        for (int j = i; j < chs.length; j++) {
            if (!visit[chs[j] - 'a']) {
                //todo ！！！！为什么要相同的字符不去尝试，因为前面尝试过了
                //todo 对于全排列来说，是否是同一个字符a不重要，重要的是a这种情况已经走过了，这个位置上不允许是a了
                //todo 这就叫做分支限界（剪枝） 提前杀死不可能的路 这个策略不可能中
                visit[chs[j] - 'a'] = true;
                swap(chs, i, j);  //在for循环里去循环剩余的所有节点，每一个都去交换然后递归尝试
                process(chs, i + 1, res);  //因为是全排列，因此i需要自增到长度后结束
                swap(chs, i, j);//在递归结束后要把节点换回去  也就是回溯
            }
        }
    }
    public static void swap(char[] chs, int i, int j) {
        char tmp = chs[i];
        chs[i] = chs[j];
        chs[j] = tmp;
    }
}

聪明绝顶的玩家

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。
【举例】
arr=[1,2,100,4]。开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，接下来
玩家 B可以拿走2或4，然后继续轮到玩家A...如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继续轮到玩家A...玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1，
让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家 A拿走。玩家A会获胜，分数为101。所以返回101。

arr=[1,100,2]。开始时，玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜，分数为100。所以返回100。

思路：

定义一个先手函数，base case：L==R，直接返回L的值。递归情况：如果选左，累加值，传递给后手函数（L+1,R），累加后手函数的结果。或者选右，累加值，传递给后手函数（L+1,R-1），累加后手函数的结果。目的是让这两个结果最大。

后手函数，base case：L==R，直接返回0，因为就一个数还被拿走了。。剩下的就是先手函数的两个结果（一左一右），并且因为对面很聪明，所以我这个结果需要取min。

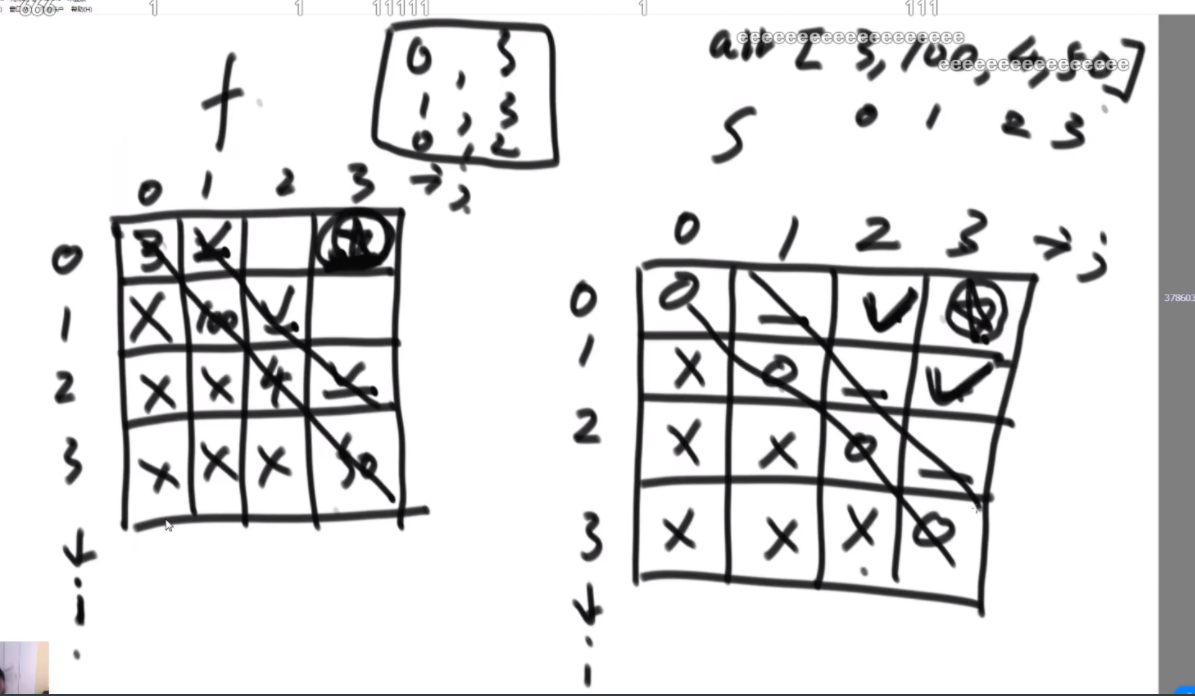
严格表结构：从P17飞过来看，这个暴力递归可以优化，通过分析建两个二维表，推出结论，f上的每个点，依赖于对应到s相同位置上的点的左侧和下侧节点，s上的点同理，依赖于f位置上的左侧和下侧节点。这种题改动态规划的需要画图。

这里两个二维表，也可以看做是三维表的一维表达。

package ZuoShen.Class09;

public class CardsInLine {
    public static int win1(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        //直接返回这个数组中，先手和后手的更大的那个值，因为这俩值是固定的
        return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
    }
    //先手函数
    public static int f(int[] arr, int i, int j) {
        if (i == j) {
            return arr[i];
        }
        return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
    }
    //后手函数
    public static int s(int[] arr, int i, int j) {
        if (i == j) {
            return 0;
        }
        return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));
    }
	//严格表结构
    public static int win2(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int[][] f = new int[arr.length][arr.length];
        int[][] s = new int[arr.length][arr.length];
        for (int j = 0; j < arr.length; j++) {
            f[j][j] = arr[j];
            for (int i = j - 1; i >= 0; i--) {
                f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
                s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
            }
        }
        return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
    }
    public static void main(String[] args) {
        int[] arr = { 1, 9, 1 };
        System.out.println(win1(arr));
        System.out.println(win2(arr));

    }
}

只用递归去逆序栈

package ZuoShen.Class09;

import java.util.Stack;

public class ReverseStackUsingRecursive {
    public static void reverse(Stack<Integer> stack) {
        if (stack.isEmpty()) {
            return;
        }
        int i = getAndRemoveLastElement(stack);
        reverse(stack); //推理同下，自己推
        stack.push(i);
    }
    //获得并移除栈低元素  用栈顶向下1 2 3举例
    //result = 1 last=递归结果   last =》3 并把1压入  回溯
    //result = 2 last=递归结果   last =》3 并把2压入  回溯，维持原条件不变
    //result = 3
    public static int getAndRemoveLastElement(Stack<Integer> stack) {
        int result = stack.pop();
        if (stack.isEmpty()) {
            return result;
        } else {
            int last = getAndRemoveLastElement(stack);
            stack.push(result);
            return last;
        }
    }
    public static void main(String[] args) {
        Stack<Integer> test = new Stack<Integer>();
        test.push(1);
        test.push(2);
        test.push(3);
        test.push(4);
        test.push(5);
        reverse(test);
        while (!test.isEmpty()) {
            System.out.println(test.pop());
        }

    }
}

数字字符转字符串的结果数

规定1和A对应、2和B对应、3和C对应...那么一个数字字符串比如"111"，就可以转化为"AAA"、"KA"和"AK"。 因为K的定义为数字的11。给定一个只有数字字符组成的字符串str，返回有多少种转化结果。

package ZuoShen.Class09;

public class ConvertToLetterString {
    public static int number(String str) {
        if (str == null || str.length() == 0) {
            return 0;
        }
        return process(str.toCharArray(), 0);
    }

    //i之前的位置，如何转化已经做过决定了
    //i... 有多少种转化的结果
    public static int process(char[] chs, int i) {
        if (i == chs.length) { //因为前面的选择都是合理的  没有两个合一个的情况  所以长度一样
            return 1;
        }
        if (chs[i] == '0') { //虽然是之前有效，但也没意义  0没有对应的 后续的情况G了 整体就只有0种有效的
            return 0;
        }
        if (chs[i] == '1') {
            int res = process(chs, i + 1); //i自己作为单独的部分（不合体），后续有多少种方法
            if (i + 1 < chs.length) {
                res += process(chs, i + 2);//i和i+1作为单独的部分（合体了）,后续有多少种方法
            }
            return res;
        }
        if (chs[i] == '2') {
            int res = process(chs, i + 1);//i自己作为单独的部分（不合体），后续有多少种方法
            //i和i+1作为单独的部分（合体了）并且没有超过26,后续有多少种方法
            if (i + 1 < chs.length && (chs[i + 1] >= '0' && chs[i + 1] <= '6')) {
                res += process(chs, i + 2);
            }
            return res;
        }
        //chs[i] == '3' ~ '9'  因为没有多余的情况  所以不用相加
        return process(chs, i + 1);
    }

    public static void main(String[] args) {
        System.out.println(number("11111"));
    }
}

装满最大货物价值的袋子

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表i号物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？

就从左到右一直试一直展开，可能性一直相加取最大。

package ZuoShen.Class09;

public class Knapsack {
    public static int maxValue1(int[] weights, int[] values, int bag) {
        return process1(weights, values, 0, 0, bag);
    }

    //i... （i往后的） 的货物自由选择，形成最大的价值返回
    //重量永远不要超过bag
    //之前做的决定，所达到的重量--alreadyweight
    public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
        //弹幕指出的问题：  （看不懂 先不改了）
        //只需要在return中的values[i]之前判断一下,是否超重就好了
        //并且第一个if不需要,还有误导含义,让人以为return 0就是超重价值不累加
//        if (alreadyweight > bag) {
//            return 0;
//        }
        if (i == weights.length) {
            return 0;
        }
        return Math.max(
                //不要第i个货物
                process1(weights, values, i + 1, alreadyweight, bag),
                //要第i个货物  但是应该去做判断吧。。。
                values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
    }

    public static int maxValue2(int[] c, int[] p, int bag) {
        int[][] dp = new int[c.length + 1][bag + 1];
        for (int i = c.length - 1; i >= 0; i--) {
            for (int j = bag; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j];
                if (j + c[i] <= bag) {
                    dp[i][j] = Math.max(dp[i][j], p[i] + dp[i + 1][j + c[i]]);
                }
            }
        }
        return dp[0][0];
    }
    public static void main(String[] args) {
        int[] weights = { 3, 2, 4, 7 };
        int[] values = { 5, 6, 3, 19 };
        int bag = 11;
        System.out.println(maxValue1(weights, values, bag));
        System.out.println(maxValue2(weights, values, bag));
    }
}

N皇后问题

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击，即要求任何两个皇后不同行、不同列，也不在同一条斜线上。给定一个整数n，返回n皇后的摆法有多少种。

n=1，返回1。n=2或3，2皇后和3皇后问题怎么摆都不行，返回0。n=8，返回92.

num1是不优化的版本，record是长度为n的一维数组，脚标代表行数，里面的值代表第几列放置了皇后。process1中，i代表行数，record代表已经放入的皇后位置，isValid验证能否在i行j列放置皇后，如果可以，记录进去，然后递归，传参的行数+1.

package class08;

public class Code09_NQueens {
	public static int num1(int n) {
		if (n < 1) {
			return 0;
		}
        //record是长度为n的一维数组，脚标代表行数，里面的值代表第几列放置了皇后
		int[] record = new int[n];
		return process1(0, record, n);
	}
	public static int process1(int i, int[] record, int n) {
		if (i == n) {
			return 1;
		}
		int res = 0;
		for (int j = 0; j < n; j++) {
			if (isValid(record, i, j)) {
				record[i] = j;
				res += process1(i + 1, record, n);
			}
		}
		return res;
	}

	public static boolean isValid(int[] record, int i, int j) {
		for (int k = 0; k < i; k++) {
			if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
                //左边代表不能在同一列||右边代表等边三角形两个直角边相等长度 在斜线上
				return false;
			}
		}
		return true;
	}
	//因为是用int来表示位，所以不能超过32   如果要超过32需要改成Long
	public static int num2(int n) {
		if (n < 1 || n > 32) {
			return 0;
		}
        //变成位数  假设n=8  upperLim=11111111   1<<n代表1左移n位
		int upperLim = n == 32 ? -1 : (1 << n) - 1;
		return process2(upperLim, 0, 0, 0);
	}

	public static int process2(int upperLim, int colLim, int leftDiaLim,
			int rightDiaLim) {
		if (colLim == upperLim) {  //如果这俩相等，说明没法再往后走了  结束了
			return 1;
		}
		int pos = 0;
		int mostRightOne = 0;
        //先取或，0代表能放置  取反代表1代表能放置，然后与upperLim与 8位数中的1代表能放置
		pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim)); 
		int res = 0;
		while (pos != 0) {  //这个循环让这一行全部走完
            //对pos取反加一再与可以得到最右侧的那个1
			mostRightOne = pos & (~pos + 1);
			pos = pos - mostRightOne;
			res += process2(upperLim, colLim | mostRightOne,//这俩或是0代表能放，1代表不能，或上之后皇后的位子又少了一个 
					(leftDiaLim | mostRightOne) << 1,//为了让斜边保持，需要左移和右移
					(rightDiaLim | mostRightOne) >>> 1);
		}
		return res;
	}

	public static void main(String[] args) {
		int n = 14;

		long start = System.currentTimeMillis();
		System.out.println(num2(n));
		long end = System.currentTimeMillis();
		System.out.println("cost time: " + (end - start) + "ms");

		start = System.currentTimeMillis();
		System.out.println(num1(n));
		end = System.currentTimeMillis();
		System.out.println("cost time: " + (end - start) + "ms");

	}
}

p9:

前缀树

何为前缀树? 如何生成前缀树?

一个字符串数组，遍历这个数组，如果有通向a这个字符的路就复用，没有就新建。

前缀树中 ，pass代表生成前缀树的过程中，这个节点被到达过多少次，end代表这个节点作为结尾出现的次数。因此在下面的图中，可以判断有多少个以ab为前缀的字符串（即ab的pass的次数），有多少以bc为结尾的次数（即bc中c的end的次数）

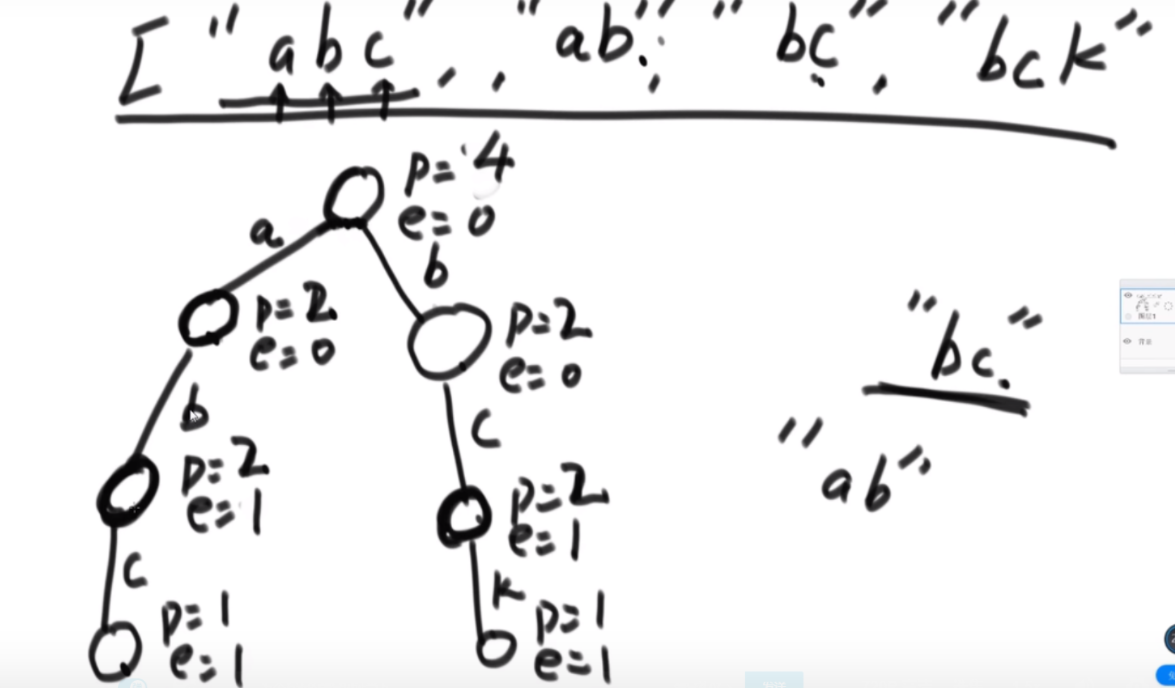
例子:一个字符串类型的数组arr1，另一个字符串类型的数组arr2。arr2中有哪些字符，是arr1中出现的？请打印。arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印。arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印 arr2中出现次数最大的前缀。

前缀树的增删改查：

package ZuoShen.Class08;

public class TrieTree {
    public static class TrieNode{
        public int pass;  //该节点走过多少次
        public int end;   //该节点作为结尾多少次
        public TrieNode[] nexts;
        //HashMap<Char,Node> nexts 如果字符种类特别多可以选择用hash表来表达路
        //TreeMap<Char,Node> nexts 如果字符种类特别多并且要求有序可以选择用有序表来表达路
        public TrieNode(){
            pass=0;
            end=0;
            //脚标为0-25  代表该节点可以有26个小写字母连接
            // 默认是null代表没有指向该脚标的字母的连接
            nexts=new TrieNode[26];
        }
    }
    public static class Trie{
        private TrieNode root;
        public Trie(){
            root=new TrieNode();
        }
        //将一个字符串插入到前缀树
        public void insert(String word){
            if(word==null){
                return;
            }
            char[] chars = word.toCharArray();
            TrieNode node = root;
            node.pass++; //根节点的pass先+1
            int index = 0;  //这个index用于控制新加入的节点放入trieNodes数组中的哪个位置
            for (int i = 0; i < chars.length; i++) {
                index=chars[i] - 'a'; //这样'a'的脚标为0，'b'的脚标为1  以此类推
                if(node.nexts[index]==null){
                    node.nexts[index]=new TrieNode();
                }
                node = node.nexts[index];
                node.pass++;
            }
            node.end++;
        }
        //删除word字符 （一次）
        public void delete(String word) {
            if (search(word) != 0) {
                char[] chs = word.toCharArray();
                TrieNode node = root;
                int index = 0;
                for (int i = 0; i < chs.length; i++) {
                    index = chs[i] - 'a';
                    if (--node.nexts[index].pass == 0) {
                        node.nexts[index] = null; //c++要去底层去析构
                        return;
                    }
                    node = node.nexts[index];
                }
                node.end--;
            }
        }
        //查询word这个单词加入过几次
        public int search(String word){
            if(word==null){
                return 0;
            }
            char[] chars = word.toCharArray();
            int index = 0;
            TrieNode node = root;
            for (int i = 0; i < chars.length; i++) {
                index = chars[i] - 'a';
                if (node.nexts[index] == null) {
                    return 0;//查找abcdefg  走到abc结束了 说明没加入过
                }
                node = node.nexts[index];
            }
            return node.end;
        }
        //查询word这个单词作为前缀加入过几次
        public int prefixNumber(String pre) {
            if (pre == null) {
                return 0;
            }
            char[] chs = pre.toCharArray();
            TrieNode node = root;
            int index = 0;
            for (int i = 0; i < chs.length; i++) {
                index = chs[i] - 'a';
                if (node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.pass;
        }
    }
}

贪心算法

定义：在某一个标准下，优先考虑最满足标准的样本，最后考虑最不满足标准的样本，最终得到一个答案的算法，叫作贪心算法。也就是说，不从整体最优上加以考虑，所做出的是在某种意义上的局部最优解。局部最优 -?-> 整体最优

贪心算法的在笔试时的解题套路
1，实现一个不依靠贪心策略的解法X，可以用最暴力的尝试
2，脑补出贪心策略A、贪心策略B、贪心策略C...
3，用解法X和对数器，去验证每一个贪心策略，用实验的方式得知哪个贪心策略正确
4，不要去纠结贪心策略的证明

最常用的两个是堆和排序

找到字典序最小的字符串拼接

题目：给定一个字符串类型的数组strs，找到一种拼接方式，使得把所有字符串拼起来之后形成的字符串具有最小的字典序。字典序：字母单词在字典中的顺序，位数一样的依次比较，如果位数不一样，将短的补长为和长的一样长，多的位用0补。

比较策略是否有效，得证明其传递性，以及每次对数组进行排序结果，不以这个数组的内容顺序而变化。

初始思路：a,b 判断a<=b，如果是 a放在前面，否则b放在前面。

贪心算法：a,b 判断 a.b<=b.a，将他们拼接起来前后两种去判断，如果是a前，否则b前

将str视作k进制的数字，那么a.b=a+b（字符串的拼接）=a×k^b长度+b=a×m(b)+b 巴拉巴拉证明省略 太难了艹 就对数器吧

代码很简单，就是比较一下，难在如何选择正确的策略。

package class07;

import java.util.Arrays;
import java.util.Comparator;

public class Code02_LowestLexicography {
	public static class MyComparator implements Comparator<String> {
		@Override
		public int compare(String a, String b) {
			return (a + b).compareTo(b + a);
		}
	}
	public static String lowestString(String[] strs) {
		if (strs == null || strs.length == 0) {
			return "";
		}
		Arrays.sort(strs, new MyComparator());
		String res = "";
		for (int i = 0; i < strs.length; i++) {
			res += strs[i];
		}
		return res;
	}
	public static void main(String[] args) {
		String[] strs1 = { "jibw", "ji", "jp", "bw", "jibw" };
		System.out.println(lowestString(strs1));

		String[] strs2 = { "ba", "b" };
		System.out.println(lowestString(strs2));

	}

}

分割金条的最小代价

一块金条切成两半，是需要花费和长度数值一样的铜板的。比如长度为20的金条，不管切成长度多大的两半，都要花费20个铜板。一群人想整分整块金条，怎么分最省铜板?
例如,给定数组{10,20,30}，代表一共三个人，整块金条长度为10+20+30=60。金条要分成10,20,30三个部分。 如果先把长度60的金条分成10和50，花费60；再把长度50的金条分成20和30，花费50；一共花费110铜板。但是如果先把长度60的金条分成30和30，花费60；再把长度30金条分成10和20，花费30；一共花费90铜板。
输入一个数组，返回分割的最小代价。

思路：把这个数组构造成小根堆，取出最小的两个，求和然后放入小根堆，以此类推。代码依旧简单

	public static int lessMoney(int[] arr) {
		PriorityQueue<Integer> pQ = new PriorityQueue<>();
		for (int i = 0; i < arr.length; i++) {
			pQ.add(arr[i]);
		}
		int sum = 0;
		int cur = 0;
		while (pQ.size() > 1) {
			cur = pQ.poll() + pQ.poll();
			sum += cur;
			pQ.add(cur);
		}
		return sum;
	}

获得投资的最大钱数

输入：
正数数组costs 正数数组profits 正数k 正数m
含义： costs[i]表示i号项目的花费 profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润) k表示你只能串行的最多做k个项目 m表示你初始的资金
说明：你每做完一个项目，马上获得的收益，可以支持你去做下一个项目。
输出：你最后获得的最大钱数。

思路：将这俩数组组成（k,v），先以花费排序放入小根堆（未解锁），然后取出小于等于当前m的项目放入以利润排序的大根堆（已解锁），取出大根堆中的第一个执行。

	public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {
		Node[] nodes = new Node[Profits.length];
		for (int i = 0; i < Profits.length; i++) {
			nodes[i] = new Node(Profits[i], Capital[i]);
		}
		PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());
		PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
		for (int i = 0; i < nodes.length; i++) {
			minCostQ.add(nodes[i]);
		}
		for (int i = 0; i < k; i++) {
			while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {
				maxProfitQ.add(minCostQ.poll());
			}
			if (maxProfitQ.isEmpty()) {
				return W;
			}
			W += maxProfitQ.poll().p;
		}
		return W;
	}

随时取得中位数

给一个数据流，搞一个结构随时可以取出他们的中位数（偶数个的时候是两个数相加除2）。

思路：搞一个大根堆一个小根堆，第一个数放进大根堆，接下来的数与大根堆堆顶比较，如果小于等于大根堆堆顶，进入大根堆，否则进入小根堆。如果大根堆和小根堆大小差距大于等于2，那么将其中多的那个的堆顶压入另一个堆。

	public static class MedianHolder {
		private PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new MaxHeapComparator());
		private PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(new MinHeapComparator());
		private void modifyTwoHeapsSize() {
			if (this.maxHeap.size() == this.minHeap.size() + 2) {
				this.minHeap.add(this.maxHeap.poll());
			}
			if (this.minHeap.size() == this.maxHeap.size() + 2) {
				this.maxHeap.add(this.minHeap.poll());
			}
		}
		public void addNumber(int num) {
			if (maxHeap.isEmpty() || num <= maxHeap.peek()) {
				maxHeap.add(num);
			} else {
				minHeap.add(num);
			}
			modifyTwoHeapsSize();
		}
		public Integer getMedian() {
			int maxHeapSize = this.maxHeap.size();
			int minHeapSize = this.minHeap.size();
			if (maxHeapSize + minHeapSize == 0) {
				return null;
			}
			Integer maxHeapHead = this.maxHeap.peek();
			Integer minHeapHead = this.minHeap.peek();
			if (((maxHeapSize + minHeapSize) & 1) == 0) {
				return (maxHeapHead + minHeapHead) / 2;
			}
			return maxHeapSize > minHeapSize ? maxHeapHead : minHeapHead;
		}

	}
	public static class MaxHeapComparator implements Comparator<Integer> {
		@Override
		public int compare(Integer o1, Integer o2) {
			if (o2 > o1) {
				return 1;
			} else {
				return -1;
			}
		}
	}
	public static class MinHeapComparator implements Comparator<Integer> {
		@Override
		public int compare(Integer o1, Integer o2) {
			if (o2 < o1) {
				return 1;
			} else {
				return -1;
			}
		}
	}

p8:

图的存储方式

1. 邻接表法（用链表存储）
2. 邻接矩阵法（用矩阵存储）
3. 。。。很多种 只要用一种数据结构将所有算法实现一遍，然后将别的数据结构转化成这个数据结构就可以了

推荐的数据结构：

public class Node {
    public int value;//结点的值
    public int in;   //该节点的入度
    public int out;  //该节点的出度
    public ArrayList<Node> nexts;  //该节点指向的那些节点
    public ArrayList<Edge> edges;  //以该节点为初始 发出去的那些边
    public Node(int value){
        this.value=value;
        in=0;
        out=0;
        nexts=new ArrayList<>();
        edges=new ArrayList<>();
    }
}
public class Edge {
    public int weight;  //边的权重
    public Node from;   //边的两头的节点 一个from 一个to
    public Node to;

    public Edge(int weight,Node from,Node to){
        this.weight=weight;
        this.from=from;
        this.to=to;
    }
}
public class Graph {
    public HashSet<Edge> edges;          //图中的边
    public HashMap<Integer,Node> nodes;  //图中的节点

    public Graph(){
        edges=new HashSet<>();
        nodes=new HashMap<>();
    }
}

图的生成

package ZuoShen.Class07;

public class GraphGenerator {
    //以二维数组形式存储的图    其中的一维数组有三项  边的权重 入度 出度
    public static Graph createGraph(Integer[][] matrix){
        Graph graph = new Graph();
        for (Integer[] integers : matrix) {
            Integer weight = integers[0];
            Integer from = integers[1];
            Integer to = integers[2];
            if (!graph.nodes.containsKey(from)) {
                graph.nodes.put(from, new Node(from));
            }
            if (!graph.nodes.containsKey(to)) {
                graph.nodes.put(to, new Node(to));
            }
            Node fromNode = graph.nodes.get(from);
            Node toNode = graph.nodes.get(to);
            Edge newEdge = new Edge(weight, fromNode, toNode);
            fromNode.nexts.add(toNode);
            fromNode.out++;
            toNode.in++;
            fromNode.edges.add(newEdge);
            graph.edges.add(newEdge);
        }
        return graph;
    }
}

宽度优先遍历BFS

图的宽度优先遍历
1，利用队列实现
2，从源节点开始依次按照宽度进队列，然后弹出
3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
4，直到队列变空

package ZuoShen.Class07;

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;

public class BFS {
    //从node出发，宽度优先遍历
    public static void bfs(Node node){
        if(node==null){
            return;
        }
        HashSet<Node> register = new HashSet<>(); //特殊情况可以替换为数组
        Queue<Node> queue = new LinkedList<>();
        register.add(node);
        queue.add(node);
        while (!queue.isEmpty()){
            node = queue.poll();
            System.out.println(node.value);
            for (Node a:node.nexts) {
                if(!register.contains(a)){
                    queue.add(a);
                    register.add(a);
                }
            }
        }
    }
}

深度优先遍历DFS

图的深度优先遍历
1，利用栈实现
2，从源节点开始把节点按照深度放入栈，然后弹出
3，每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
4，直到栈变空

package ZuoShen.Class07;

import java.util.HashSet;
import java.util.Stack;

public class DFS {
    public static void dfs(Node node){
        HashSet<Node> set = new HashSet<>();
        Stack<Node> stack = new Stack<>();
        set.add(node);
        stack.push(node);
        while (!stack.isEmpty()){
            node=stack.pop();
            System.out.println(node.value);
            for(Node next:node.nexts){
                if(!set.contains(next)){
                    set.add(next);
                    stack.push(node);  //发现一个没访问过的  直接一条路走到黑
                    stack.push(next);
                    System.out.println(next.value);
                    break;
                }
            }
        }
    }
}

拓扑排序

先找到第一个入度为0的节点，然后删掉它和它的所有影响，再找下一个入度为0 的节点，如果发现找不到了，说明有环。

适用范围：要求有向图，且有入度为0的节点，且没有环.

package ZuoShen.Class07;

import java.util.*;

public class TopologySort {
    //directed graph and no loop
    public static List<Node> topologysort(Graph graph){
        //Node 代表节点  Integer代表该节点的入度
        HashMap<Node,Integer> inMap = new HashMap<>();
        //zeroNodes 是入度为0的节点的队列
        Queue<Node> zeroNodes = new LinkedList<>();
        for(Node node:graph.nodes.values()){
            inMap.put(node,node.in);
            if(node.in==0){
                zeroNodes.add(node);
            }
        }
        //拓扑排序的结果，一次加入result中
        ArrayList<Node> result = new ArrayList<>();
        while (!zeroNodes.isEmpty()){
            Node cur = zeroNodes.poll();
            result.add(cur);
            for (Node a:cur.nexts){
//                a.in--;  不是节点去--而是inMap中的入度要--
                inMap.put(a,inMap.get(a)-1);//相同的key会替换掉之前的
                if(a.in==0){
                    zeroNodes.add(a);
                }
            }
        }
        return result;
    }

}

kruskal算法

与Prim算法共同用于生成最小生成树，最小生成树的定义：所有节点用树的形式表示（没有环）且所有边的权值之和为最小。

算法思路：先找到最小的边，连上，然后找到第二小的边，连上，判断是否成环，找到第三小的边，连上，判断是否成环，如果成环，舍弃这个边，继续找下一小的边。。。依次类推，遍历所有的边。

代码思路：把所有元素依次生成一个Arraylist对应，如果在最小生成树中，则合并List。所有边先按照权值进入小根堆，从小到大拿取边。先给每个点生成一个list，然后放入hashmap中，判断下一个边是否会成环，就可以直接判断from和to是否集合一样，因为最开始都是一个元素的集合，合并入一个边后，这个边的from和to的list会更新为两个元素的集合，因此如果两个点在图中，那么集合必定一样，因此可以判断是否成环。

适用范围：要求无向图

因为有可能边会先连成两个小片 然后这两个小片再相连，因为有这种需求需要并查集这个有点难，就没讲。

没有用到并查集的代码：

package ZuoShen.Class07;

import java.util.*;

public class Kruskal {
    //可以用并查集优化！！！
    //把所有元素依次生成一个Arraylist对应
    HashMap<Node,ArrayList<Node>> map = new HashMap<>();
    public  List<Edge> kruskal(Graph graph){
        //Kruskal的结果，加入result中
        ArrayList<Edge> result = new ArrayList<>();
        PriorityQueue<Edge> edgeweight = new PriorityQueue<>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.weight-o2.weight;
            }
        });
        for (Edge edge:graph.edges){  //M条边
            edgeweight.add(edge);   //O(logM)
            //因为是无向图，因此直接放入所有from就是所有节点。
            ArrayList<Node> temp = new ArrayList<>();
            temp.add(edge.from);
            map.put(edge.from,temp);
        }
        while (!edgeweight.isEmpty()){//M条边
            Edge edge = edgeweight.poll();//O(logM)
            if(!judgeLoop(edge.from,edge.to)){
                union(edge.from,edge.to);
//                result.add(edge.from);//最小生成树用点表示可能会重复
//                result.add(edge.to);//因此选择用边去表示
                result.add(edge);
            }
        }
        return result;
    }
    public  boolean judgeLoop(Node from,Node to){
        return map.get(from)==map.get(to);//如果相等，说明这俩集合一样，会成环
    }
    public void union(Node from,Node to){
        ArrayList<Node> fromList = map.get(from);
        ArrayList<Node> toList = map.get(to);
        //这里的左神版本for循环里面写的put，有点奇怪  是我效率低了吗？？？
        fromList.addAll(toList);
        map.put(to,fromList);
        map.put(from,fromList);
    }
}

并查集的实现：

package class06;
//undirected graph only
public class Code04_Kruskal {
	// Union-Find Set
	public static class UnionFind {
		private HashMap<Node, Node> fatherMap;
		private HashMap<Node, Integer> rankMap;
		public UnionFind() {
			fatherMap = new HashMap<Node, Node>();
			rankMap = new HashMap<Node, Integer>();
		}
		private Node findFather(Node n) {
			Node father = fatherMap.get(n);
			if (father != n) {
				father = findFather(father);
			}
			fatherMap.put(n, father);
			return father;
		}
		public void makeSets(Collection<Node> nodes) {
			fatherMap.clear();
			rankMap.clear();
			for (Node node : nodes) {
				fatherMap.put(node, node);
				rankMap.put(node, 1);
			}
		}
		public boolean isSameSet(Node a, Node b) {
			return findFather(a) == findFather(b);
		}
		public void union(Node a, Node b) {
			if (a == null || b == null) {
				return;
			}
			Node aFather = findFather(a);
			Node bFather = findFather(b);
			if (aFather != bFather) {
				int aFrank = rankMap.get(aFather);
				int bFrank = rankMap.get(bFather);
				if (aFrank <= bFrank) {
					fatherMap.put(aFather, bFather);
					rankMap.put(bFather, aFrank + bFrank);
				} else {
					fatherMap.put(bFather, aFather);
					rankMap.put(aFather, aFrank + bFrank);
				}
			}
		}
	}
	public static class EdgeComparator implements Comparator<Edge> {
		@Override
		public int compare(Edge o1, Edge o2) {
			return o1.weight - o2.weight;
		}
	}
	public static Set<Edge> kruskalMST(Graph graph) {
		UnionFind unionFind = new UnionFind();
		unionFind.makeSets(graph.nodes.values());
		PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
		for (Edge edge : graph.edges) {
			priorityQueue.add(edge);
		}
		Set<Edge> result = new HashSet<>();
		while (!priorityQueue.isEmpty()) {
			Edge edge = priorityQueue.poll();
			if (!unionFind.isSameSet(edge.from, edge.to)) {
				result.add(edge);
				unionFind.union(edge.from, edge.to);
			}
		}
		return result;
	}
}

Prim算法

算法思路：假设所有边都未解锁，先找到一个节点，放入set，然后解锁该节点所连的所有边，选择其中权值最小的，将第二个节点放入set，再解锁第二个节点所连的所有边，找到权值最小的，依次类推，如果权值一样，判断那个to到的节点是否在set中。

代码思路：解锁的边放入小根堆。先取一个点，将所有边放入小根堆，然后从小根堆中取出，判断to是否满足条件，满足就填入边，不满足就再在小根堆中取。

package ZuoShen.Class07;
import java.util.*;
public class Prim {
    public ArrayList<Edge> prim(Graph graph){
        ArrayList<Edge> result = new ArrayList<>();
        //如果被放入最小生成树中 就加入该节点
        HashSet<Node> selectedNode = new HashSet<>();
        PriorityQueue<Edge> edgeweight = new PriorityQueue<>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.weight-o2.weight;
            }
        });
        for(Node node:graph.nodes.values()){
            //先找到一个节点   解锁它的所有边
            if(!selectedNode.contains(node)){
                //将第一个节点放入图中
                selectedNode.add(node);
                for(Edge edge:node.edges){
                    edgeweight.add(edge);
                }
                //取出当前最小的边
                Edge cur = edgeweight.poll();
                Node toNode = cur.to;
                //如果这个边的节点已经在树中，则不去进行操作
                //主要是因为边会重复放入，但不会进入下面的if
                if(!selectedNode.contains(toNode)){
                    selectedNode.add(toNode);
                    result.add(cur);
                    //然后将这个节点的所有边放入小根堆中
                    for (Edge edge:toNode.edges){
                        edgeweight.add(edge);
                    }
                }
            }
        }
        return result;
    }
}

Dijkstra算法

适用范围：可以有权值为负数的边，但是不能有累加和为负数的环，因为可以在这个环里越转越小，最短就没有意义了

单元最短路径算法：规定一个出发点，找到其他点的最短路径。

思路：先写出A到ABCDE的距离，然后按每次找到最小的距离更新，更新完成后就锁死A到这个节点的距离，不再改变。

代码思路：用Set控制是否锁住，每次找到最小的边的节点，如果遇到过就更新，把map中的值和这次的值取min，没遇到过就放入。在找到最小的边的时候，使用的是遍历，因为使用小根堆而且频繁更新的代价和遍历差不多，这里可以使用堆的重写来优化，即自己重新实现节点的更新后的移动操作。

未使用堆的重写

package ZuoShen.Class07;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
public class Dijkstra {
    //dijkstra返回值为当前节点与头结点到当前节点的距离
    public static HashMap<Node,Integer> dijkstra(Node head){
        HashMap<Node, Integer> distanceMap = new HashMap<>();
        //先将头放进去  未放入的视为无穷大小
        distanceMap.put(head, 0);
        HashSet<Node> selectedNodes = new HashSet<>();
        //找到当前该更新的节点（锁定）
        Node minNode =  getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
        while (minNode!=null){
            int distance = distanceMap.get(minNode);
            for (Edge edge:minNode.edges){
                Node toNode = edge.to;
                if(!distanceMap.containsKey(toNode)){
                    distanceMap.put(toNode,distance+edge.weight);
                }else {
                    distanceMap.put(toNode,Math.min(distance+edge.weight,distanceMap.get(toNode)));
                }
            }
            selectedNodes.add(minNode);
            minNode =  getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
        }   
        return distanceMap;
    }
    //找到不在路径中，并且距离最短的节点  就是更新完路径距离最近的节点后更新第二近第三近的
    public static Node getMinDistanceAndUnselectedNode(HashMap<Node,Integer> distanceMap,HashSet<Node> touchedNodes){
        Node minNode = null;
        int minDistance = Integer.MAX_VALUE;
        for(Map.Entry<Node,Integer> entry:distanceMap.entrySet()){
            Node node = entry.getKey();
            int distance = entry.getValue();
            if(!touchedNodes.contains(node) && distance<minDistance){
                minNode=node;
                minDistance=distance;
            }
        }
        return minNode;
    }
}

使用堆的重写（日后研究）：

package class06;

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map.Entry;

// no negative weight
public class Code06_Dijkstra {

	public static class NodeRecord {
		public Node node;
		public int distance;

		public NodeRecord(Node node, int distance) {
			this.node = node;
			this.distance = distance;
		}
	}

	public static class NodeHeap {
		private Node[] nodes;
        //用于去一下子找到Node在树中的位置
		private HashMap<Node, Integer> heapIndexMap;
        //用于记录初始节点到Node的距离
		private HashMap<Node, Integer> distanceMap;
		private int size;

		public NodeHeap(int size) {
			nodes = new Node[size];
			heapIndexMap = new HashMap<>();
			distanceMap = new HashMap<>();
			this.size = 0;
		}

		public boolean isEmpty() {
			return size == 0;
		}

		public void addOrUpdateOrIgnore(Node node, int distance) {
			if (inHeap(node)) {
                //在堆中的节点，需要去heapify更新一下
				distanceMap.put(node, Math.min(distanceMap.get(node), distance));
                //这里更新距离，要么没更新，要么变小了  需要往上走
				insertHeapify(node, heapIndexMap.get(node));
			}
			if (!isEntered(node)) {
                //新建节点
				nodes[size] = node;
				heapIndexMap.put(node, size);
				distanceMap.put(node, distance);
				insertHeapify(node, size++);
			}
            //剩下的就是进来过但没在堆上的，不用管
		}

		public NodeRecord pop() {
			NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));
            //堆去掉堆顶  把最后一个换上来
			swap(0, size - 1);
			heapIndexMap.put(nodes[size - 1], -1);
			distanceMap.remove(nodes[size - 1]);
			nodes[size - 1] = null;
			heapify(0, --size);
			return nodeRecord;
		}

		private void insertHeapify(Node node, int index) {
			while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {
				swap(index, (index - 1) / 2);
				index = (index - 1) / 2;
			}
		}

		private void heapify(int index, int size) {
			int left = index * 2 + 1;
			while (left < size) {
				int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])
						? left + 1 : left;
				smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;
				if (smallest == index) {
					break;
				}
				swap(smallest, index);
				index = smallest;
				left = index * 2 + 1;
			}
		}

        //判断Node有没有进来过   如果进来了又弹出，会把value置为-1
		private boolean isEntered(Node node) {
			return heapIndexMap.containsKey(node);
		}
         //判断Node是否在堆上
		private boolean inHeap(Node node) {
			return isEntered(node) && heapIndexMap.get(node) != -1;
		}

		private void swap(int index1, int index2) {
			heapIndexMap.put(nodes[index1], index2);
			heapIndexMap.put(nodes[index2], index1);
			Node tmp = nodes[index1];
			nodes[index1] = nodes[index2];
			nodes[index2] = tmp;
		}
	}

	public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
		NodeHeap nodeHeap = new NodeHeap(size);
		nodeHeap.addOrUpdateOrIgnore(head, 0);//没出现过就add 出现过如果比原来的小就update 如果比原来的大就ignore  还有个隐藏功能，不会去看那些已经看过的节点，因为一定不会更小
		HashMap<Node, Integer> result = new HashMap<>();
		while (!nodeHeap.isEmpty()) {
			NodeRecord record = nodeHeap.pop();
			Node cur = record.node;
			int distance = record.distance;
			for (Edge edge : cur.edges) {
				nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
			}
			result.put(cur, distance);
		}
		return result;
	}
}

p7:

判断一棵树是不是搜索二叉树

搜索二叉树就是指每个子树左子树节点都比它小，右子树节点都比它大。

思路：中序遍历如果是顺序递增的 说明是搜索二叉树，如果有一个不是递增，则不是。

利用套路：左树是否是搜索二叉树，左树的最大值是否小于当前节点值；右树是否是搜索二叉树，右树的最小值是否大于当前节点值。然后总结一下：左右子树都返回该子树是否是搜索二叉树，然后返回该子树的最大值和最小值。

package ZuoShen.Class06;

import java.util.Stack;

public class IsBST {
    public static void main(String[] args) {

    }
    public static int preValue=Integer.MIN_VALUE;
    public static boolean isBST1(Node head){
        //方法一：递归形式中序遍历的判断
        if(head==null){
            return true;
        }
        boolean isLeftBst = isBST1(head.left);
        if(!isLeftBst){
            return false;
        }
        if(head.value<preValue){
            return false;
        }else {
            preValue= head.value;
        }
        return isBST1(head.right);
    }
    public static boolean isBST2(Node head) {
        //方法二：非递归形式中序遍历的判断
        System.out.print("in-order: ");
        if(head!=null){
            Stack<Node> nodes = new Stack<>();
            while (!nodes.empty()||head!=null){
                int preValue = Integer.MIN_VALUE;
                if(head!=null){
                    nodes.push(head);
                    head=head.left;
                }else {
                    head=nodes.pop();
                    if(head.value<=preValue){
                        return false;
                    }else {
                        preValue=head.value;
                    }
                    head=head.right;
                }
            }
        }
        return true;
    }
    public static class ReturnData{
        public boolean isBST;
        public int min;
        public int max;
        public ReturnData(boolean isBST,int min,int max){
            this.isBST=isBST;
            this.max=max;
            this.min=min;
        }
    }
    public static ReturnData process(Node x){
        //方法三：利用套路然后实现
        if(x==null){
//            return new ReturnData(true,)//因为这里最大值和最小值无法设置初始值所以设为null
            return null;
        }
        ReturnData leftData = process(x.left);
        ReturnData rightData = process(x.right);
        int min = x.value;
        int max = x.value;
        if(leftData!=null){
            min = Math.min(min,leftData.min);
            max = Math.max(min,leftData.max);
        }
        if(rightData!=null){
            min = Math.min(min,rightData.min);
            max = Math.max(min,rightData.max);
        }
        boolean isBST = true;
        if(leftData!=null&&(!leftData.isBST||leftData.max>=x.value)){
            isBST=false;
        }
        if(rightData!=null&&(!rightData.isBST||x.value>=rightData.min)){
            isBST=false;
        }
        return new ReturnData(isBST,min,max);
    }
}
class Node{
    int value;
    Node left;
    Node right;
    Node(int value){
        this.value = value;
    }
}

方法四：Morris中序遍历修改

//Morris 中序遍历
    public static boolean isBST(Node head) {
        if (head == null) {
            return true;
        }
        Node cur = head;
        Node mostRight = null;
        int preValue = Integer.MIN_VALUE;
        while (cur != null) {  // 过流程，cur为空结束
            mostRight = cur.left;  //mostRight是cur左孩子
            if (mostRight != null) {  // cur有左子树
                //原本是指向null  但是也有可能修改后指向cur 找到任意一种情况就停
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                //mostRight变成左树上的最右节点
                if (mostRight.right == null) { //第一次来到cur节点
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {//第二次来到cur节点，把指针弄回去然后往右走
                    mostRight.right = null;
                }
            }
//            System.out.print(cur.value + " ");  
            //把打印输出改成比较
            if (cur.value <= preValue) {
                return false;
            }
            //如果cur没有左孩子 直接往右走  情况1
            preValue= cur.value;
            cur = cur.right;
        }
        return true;
    }

如何判断一颗二叉树是完全二叉树？

思路：1.如果有右孩子没有左孩子直接返回false 2.在满足1的前提下，如果出现了第一个左右孩子不都存在的节点，那么后续的节点都必须是叶子节点。（遍历顺序为层序遍历）

package ZuoShen.Class06;
import java.util.LinkedList;
import java.util.Queue;
public class IsCST {
    public static void main(String[] args) {

    }
    public static boolean isCST(Node head){
        //层序遍历 来判断是否是满二叉树
        Queue<Node> nodes = new LinkedList<>();
        boolean leaf = false; //通过leaf判断是否经过左右孩子不全的节点  如果经过后，后续节点都应该为叶子节点
        Node l=null;
        Node r=null;
        if(head!=null){
            nodes.add(head);
            while (!nodes.isEmpty()){
                head = nodes.poll();
                l = head.left;
                r = head.right;
                if((leaf&&(l!=null||r!=null)) //遇到过左右孩子不全的节点后，leaf为true;右侧如果左右孩子有一个就为true，并返回false
                   || (l==null&&r!=null)    //无左孩子有右孩子直接false
                ){
                    return false;
                }
                if(l!=null){
                    nodes.add(head.left);
                }
                if(r!=null){
                    nodes.add(head.right);
                }
                if(l==null || r==null){
                    leaf=true;//遇到左右孩子不全时，则后面必须都为叶子节点
                }
            }
        }
        return true;
    }
}

如何判断一颗二叉树是否是满二叉树？

方法一：先求满二叉树深度L，然后求出二叉树节点个数N，判断是否满足条件N=2^L-1

方法二：套路

package ZuoShen.Class06;

public class IsFullTree {
    public static class ReturnData{
        public int height;
        public int nodes;
        public ReturnData(int height,int nodes){
            this.height=height;
            this.nodes=nodes;
        }
    }

    public static ReturnData f(Node x){
        //方法二  用套路
        if(x==null){
            return new ReturnData(0,0);
        }
        ReturnData leftData = f(x.left);
        ReturnData rightData = f(x.right);
        int height = Math.max(leftData.height, rightData.height)+1;
        int nodes = leftData.nodes+rightData.nodes+1;
        return new ReturnData(height,nodes);
    }
}

如何判断一颗二叉树是否是平衡二叉树？

平衡二叉树：每一棵子树左树与右树的高度差不超过1

思路：左子树必须是平衡二叉树，右子树必须是平衡二叉树，左树与右树的差不能超过1，三个条件确定，左树与右树返回的内容都为（高度，是否为平衡二叉树），于是就可以将该题分解成递归形式。

package ZuoShen.Class06;

public class IsBalancedTree {
    
    public static boolean IsBalanced(Node head){
       return process(head).isBalanced;
    }
    public static class ReturnType{
        public boolean isBalanced;
        public int height;
        ReturnType(boolean isBalanced,int height){
            this.isBalanced=isBalanced;
            this.height = height;
        }
    }
    public static ReturnType process(Node x){
        if(x==null){
            return new ReturnType(true,0);
        }
        ReturnType leftData = process(x.left);
        ReturnType rightData = process(x.right);
        int height = Math.max(leftData.height,rightData.height)+1;
        boolean isBalanced = leftData.isBalanced&&rightData.isBalanced&&Math.abs(leftData.height-rightData.height)<2;
        return new ReturnType(isBalanced,height);
    }
}

找到最低公共祖先节点

题目：给定两个二叉树的节点node1和node2，找到他们的最低公共祖先节点

方法一：利用一个map构件节点向上找父节点的效果，利用set查找两者第一个相同的向上找到的父节点。

方法二：递归，先分析情况只有两种，第一种是o1是o2的LCA或o2是o1的LCA；第二种是o1与o2不互为LCA，需要通过汇聚的方式找到LCA。思路：如果是null或o1或o2直接返回，然后如果左右子树都不是null，则返回当前节点，如果左子树返回null，则返回右子树的节 点，如果右子树返回null则返回左子树的节点。

package ZuoShen.Class06;

import java.util.HashMap;
import java.util.HashSet;

public class LowestCommonAncestor {
    public static Node lca (Node head,Node o1,Node o2){
        if(head==null||head==o1||head==o2){
            return head;
        }
        Node left = lca(head.left,o1,o2);
        Node right = lca(head.right,o1,o2);
        if(left!=null&&right!=null){
            return head;
        }
        return left==null?right:left;
    }
    public static Node lca2 (Node head,Node o1,Node o2){
        //方法一：利用一个map构件节点向上找父节点的效果，利用set查找两者第一个相同的向上找到的父节点
        HashMap<Node,Node> fatherMap = new HashMap<>();
        fatherMap.put(head,head);//放入head的映射
        process(head,fatherMap);
        HashSet<Node> set1 = new HashSet<>();
        Node cur = o1;
        while (cur!=fatherMap.get(cur)){ //自己等于自己的映射  只有head会触发这个条件
            set1.add(fatherMap.get(cur));
            cur=fatherMap.get(cur);
        }
        cur = o2;
        while (cur!=fatherMap.get(cur)){
            if(set1.contains(cur)){  //当找到第一个时，就直接return
                return cur;
            }
            cur=fatherMap.get(cur);
        }
        return null;//感觉这个return没意义 如果符合题设 o1,o2都在head树中
    }
    public static void process(Node head,HashMap<Node,Node> fatherMap){
        //该函数的作用就是将所有节点(出去根节点)将他们和他们的父节点的映射放入map中
        if(head==null){
            return;
        }
        fatherMap.put(head.left,head);
        fatherMap.put(head.right,head);
        process(head.left,fatherMap);
        process(head.right,fatherMap);
    }
}

寻找后继节点

后继节点的定义：在二叉树的中序遍历的序列中， node的下一个节点叫作node的后继节点。

【题目】 现在有一种新的二叉树节点类型如下:

public class Node { 
	public int value; 
	public Node left; 
	public Node right; 
	public Node parent; 
	public Node(int val) { 
	value = val; 
	} 
}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。 假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。

只给一个在二叉树中的某个节点node，请实现返回node的后继节点的函数。

方法一可以先中序遍历然后存入一个List,然后再遍历找到当前节点的下一个节点，但是时间复杂度是O(N)，方法二要求时间复杂度为O(K)，其中K为两个节点的距离，这里只讨论方法二.

思路：分情况讨论，1.当x有右子树的时候，后继节点y为右子树的最左侧节点。2.当x无右子树时，y为x向上寻找父节点，当父节点是其父节点的左孩子时，该父节点的父节点为y。情况1的特殊情况：该树只有右孩子时，最后一个节点的后继节点不会进入情况1，因为右子树为空，因此情况2需要解决这个特殊情况。

package ZuoShen.Class06;

public class getSuccessorNode {
    public static class Node{
        public int value;
        public Node left;
        public Node right;
        public Node parent;
        public Node(int val) {
            value = val;
        }
    }
    public static Node getSuccessorNode(Node node){
        if(node==null){
            return null;
        }
        if(node.right!=null){
            return getLeftMost(node);
        }else {
            Node parent = node.parent;
            while (parent!=null&&node!=parent.left){
                node = parent;
                parent=parent.parent;
            }
            return parent;
        }
        
    }
    public static Node getLeftMost(Node node){
        if(node==null){
            return null;
        }
        while (node.left!=null){
            node=node.left;
        }
        return node;
    }
}

二叉树的序列化和反序列化

就是内存里的一棵树如何变成字符串形式，又如何从字符串形式变成内存里的树

如何判断一颗二叉树是不是另一棵二叉树的子树？

思路：先序列化，将一棵树遍历（先序遍历），然后空就用#代替，存储成一个字符串。然后反序列化就是用一个队列将字符串拆成值并一一压入，再递归构建树。

package ZuoShen.Class06;
import ZuoShen.Class06.getSuccessorNode.Node;
import java.util.LinkedList;
import java.util.Queue;
public class SerializeAndReconstructTree {
    public static String serialByPre(Node head){
        if(head==null){
            return "#_";
        }
        String res = head.value+"_";
        res+=serialByPre(head.left);
        res+=serialByPre(head.right);
        return res;
    }
    public static Node reconByPreString(String preStr){
        String[] values = preStr.split("_");
        Queue<String> queue = new LinkedList<>();
        for (int i = 0; i < values.length; i++) {
            queue.add(values[i]);
        }
        return reconPreOrder(queue);
    }
    public static Node reconPreOrder(Queue<String> queue){
        String value = queue.poll();
        if(value.equals("#")){
            return null;
        }
        Node cur = new Node(Integer.parseInt(value));
        cur.left = reconPreOrder(queue);
        cur.right = reconPreOrder(queue);
        return cur;
    }
}

**折纸问题 **

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后 展开。

此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。

如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从 上到下依次是下折痕、下折痕和上折痕。

给定一个输入参数N，代表纸条都从下边向上方连续对折N次。

请从上到下打印所有折痕的方向。

例如:N=1时，打印: down N=2时，打印: down down up

思路：试验一下会发现，每次折完之后，会在每个上一次出现的痕迹处上面出现一个凹痕下面出现一个凸痕，其实可以理解为树，这个数根节点是凹痕，然后所有左子树的根节点都是凹痕，所有右子树的根节点都是凸痕。然后通过中序遍历递归去实现打印。

package ZuoShen.Class06;

public class PaperFolding {

    public static void main(String[] args) {
        int N = 3;
        printAllFolds(N);
    }

    public static void printAllFolds(int N){
        printProcess(1,N,true);
    }

    //递归过程，来到了某一个节点
    //i是节点的层数，N一共的层数，down==ture代表凹   down==false 代表凸
    public static void printProcess(int i,int N,boolean down){
        if(i>N){
            return;
        }
        printProcess(i+1,N,true);
        System.out.println(down?"凹":"凸");
        printProcess(i+1,N,false);
    }
}

二叉树题目套路

先将题目分成两个子树，让左右子树同时返回相同类型的值，然后生成以该节点为根的树的returnData 依次递归

可以解决一切 树形DP问题 DP（动态规划 dynamic planning）

p6:

两个链表相交的一系列问题

• （两个链表中是否有相同内存地址的节点）

  【题目】给定两个可能有环也可能无环的单链表，头节点head1和head2。请实 现一个函数，如果两个链表相交，请返回相交的 第一个节点。如果不相交，返 回null

  【要求】如果两个链表长度之和为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

  首先判断是否有环：

  方法一：用额外空间，遍历链表，每到一个节点就判断是否在Set里，如果突然发现在了。说明是第一个入环节点。

  方法二：快慢指针，慢指针一定不会走够两圈以上，在环内相遇时，将快指针放到开头，慢指针原地不动。然后两个开始一次走一步，最后会在入环节点相遇。

  假设两个链表都没环：

  先统计head1到end1并且记住长度假设是100，然后统计head2和end2并且记住长度假设是80。如果end1！=end2则没有相交部分，如果一样，则head1先走20步，然后一起走直到找到相同内存的节点，即相交节点。可以通过n记录链表一和二的长度之差，节约一个变量。

  假设两个链表都有环： 分三种情况 假设链表一的头为head1，入环节点loop1，另一个为head2,入环节点为loop2

  1. 两个链表各不相交

  2. 两个链表的入环节点相同：

     当loop1==loop2时，变成了两个无环链表找共用部分，只不过尾端不是end而是loop。

  3. 两个链表的入环节点不同

     区分1 3的方法就是让loop1一直走，在转回自己的过程中如果能遇到loop2就是情况3（返回loop1或loop2都可以），否则就是情况1。

  package ZuoShen.Class04;
  
  public class FindFirstIntersectNode {
      public static void main(String[] args) {
          // 1->2->3->4->5->6->7->null
          Node head1 = new Node(1);
          head1.next = new Node(2);
          head1.next.next = new Node(3);
          head1.next.next.next = new Node(4);
          head1.next.next.next.next = new Node(5);
          head1.next.next.next.next.next = new Node(6);
          head1.next.next.next.next.next.next = new Node(7);
  //
  //        // 0->9->8->6->7->null
          Node head2 = new Node(0);
          head2.next = new Node(9);
          head2.next.next = new Node(8);
          head2.next.next.next = head1.next.next.next.next.next; // 8->6
          System.out.println(getIntersectNode(head1, head2).value);
  
          // 1->2->3->4->5->6->7->4...
          head1 = new Node(1);
          head1.next = new Node(2);
          head1.next.next = new Node(3);
          head1.next.next.next = new Node(4);
          head1.next.next.next.next = new Node(5);
          head1.next.next.next.next.next = new Node(6);
          head1.next.next.next.next.next.next = new Node(7);
          head1.next.next.next.next.next.next = head1.next.next.next; // 7->4
  
          // 0->9->8->2...
          head2 = new Node(0);
          head2.next = new Node(9);
          head2.next.next = new Node(8);
          head2.next.next.next = head1.next; // 8->2
          System.out.println(getIntersectNode(head1, head2).value);
  
          // 0->9->8->6->7->4->5->6..
          head2 = new Node(0);
          head2.next = new Node(9);
          head2.next.next = new Node(8);
          head2.next.next.next = head1.next.next.next.next.next; // 8->6
          System.out.println(getIntersectNode(head1, head2).value);
      }
      public static Node getIntersectNode(Node head1, Node head2) {
          if (head1==null||head2==null){
              return null;
          }
          Node loop1 = getLoopNode(head1);
          Node loop2 = getLoopNode(head2);
          if(loop1==null&&loop2==null){
              return noloop(head1,head2);
          }
          if(loop1!=null&&loop2!=null){
              return bothLoop(head1,loop1,head2,loop2);
          }
          return null;  //一个有环一个无环则直接Null 因为不可能相交
      }
  
      //获取入环节点 如果无环返回null
      public static Node getLoopNode(Node head) {
          if(head==null||head.next==null||head.next.next==null){
              return null;   //至少得三个元素才能构成环
          }
          Node fast=head.next.next;
          Node slow=head.next;
          while (slow!=fast){
              if(fast.next==null||fast.next.next==null){
                  return null;
              }
              slow=slow.next;
              fast=fast.next.next;
          }
          //此时fast和slow在同一个位置上
          fast=head;
          while (fast!=slow){   //将其中一个节点放到头上，然后一步一步走，再次相遇就是入环节点。
              slow=slow.next;   //这里好像是数学推论
              fast=fast.next;
          }
          return fast;
      }
      //两个链表都是无环的情况
      public static Node noloop(Node head1,Node head2){
          Node cur1 = head1;
          Node cur2 = head2;
          int n = 0;  //代表链表1长度-链表2长度 可以节约变量
          while (cur1.next!=null){
              n++;
              cur1=cur1.next;
          }
          while (cur2.next!=null){
              n--;
              cur2=cur2.next;
          }
          if(cur1!=cur2){ //当两个的结尾节点内存地址不相等时，说明该无环链表不可能相交
              return null;
          }
          cur1 = n>0?head1:head2;    //长的放在cur1
          cur2 = cur1==head1?head2:head1; //另一个放在cur2
          n=Math.abs(n);
          while (n!=0){
              n--;
              cur1=cur1.next;
          }
          while (cur1!=cur2){
              cur1=cur1.next; //走到最后还不相等就会都走到null,会跳出循环因为都是null
              cur2=cur2.next;
  
          }
          return cur1;
      }
      //两个链表都是有环的情况
      public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
          //此时分3种，两个有环链表不相交；相交且入环节点相同；相交且入环节点不同
          //首先第二种
          if(loop1==loop2){
              Node cur1 = head1;
              Node cur2 = head2;
              int n = 0;
              while (cur1 != loop1) {
                  cur1=cur1.next;
                  n++;
              }
              while (cur2 != loop2) {
                  cur2=cur2.next;
                  n--;
              }
              cur1 = n>0?head1:head2;
              cur2 = cur1==head1?head2:head1;
              n = Math.abs(n);
              while (n!=0){
                  cur1=cur1.next;
                  n--;
              }
              while (cur1!=cur2){
                  cur1=cur1.next;
                  cur2=cur2.next;
              }
              return cur1;
          }else {
              //此时为情况1和情况3
              Node cur1 = loop1.next;
              while (cur1!=loop1){
                  if(cur1==loop2){
                      return loop1; //情况3  随便返回一个都行
                  }
                  cur1=cur1.next;
              }
              return null;  //情况1  loop1走了一圈发现没有loop2 说明没相交
          }
      }
  }
  

二叉树的各种遍历

二叉树节点结构 第一层1 第二层2 3 第三层 4 5 6 7

递归序：1，2，4，4，4，5，5，5，2，1，3，6，6，6，3，7，7，7，3，1 相当于第一次到自己的时候输出一下，然后左子树走完后输出一下，右子树走完后输出一下。这是递归实现，所有的递归都可以用非递归替代。

先序遍历（头左右）：1，2，4，5，3，6，7 相当于递归序里第一次来到的时候打印，第二三次到的时候什么也不做

中序遍历（左头右）：4，2，5，1，6，3，7 相当于递归序里第二次来到的时候打印，第一三次到的时候什么也不做

后序遍历（左右头）：4，2，5，1，6，3，7 相当于递归序里第三次来到的时候打印，第一二次到的时候什么也不做

用栈实现：

先序遍历（头左右）：压入根节点 相当于深度优先遍历

1. 从栈中弹出一个节点cur
2. 打印（处理）cur
3. 先压右再压左（如果有）
4. 循环上面3步

后序遍历（左右头）:

方法一：

1. 从栈中弹出一个节点cur并将其放入收集栈中

2. 先压左再压右（如果有）

3. 循环上面2步

   最后收集栈中依次弹出打印就是后序遍历

方法二：

先看栈顶元素有无左孩子，有就入栈，这里完成左边界入栈。然后从栈顶peek，如果该节点没有左右孩子，则pop掉并打印，并且将该元素赋给变量h，再peek栈顶元素，这个节点因为是h的父元素，所以看有没有右孩子，如果有，将右孩子压入栈。将该节点右孩子处理完后，此节点被pop，以此类推。

中序遍历（左头右）：

1. 每棵子树左边界进栈
2. 依次弹出的时候打印
3. 如果弹出的节点有右子树，则对该节点的右子树进行上面两步循环

package ZuoShen.Class05;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class BinaryTreeTraversal {
    public static void main(String[] args) {
        Node head = new Node(5);
        head.left = new Node(3);
        head.right = new Node(8);
        head.left.left = new Node(2);
        head.left.right = new Node(4);
        head.left.left.left = new Node(1);
        head.right.left = new Node(7);
        head.right.left.left = new Node(6);
        head.right.right = new Node(10);
        head.right.right.left = new Node(9);
        head.right.right.right = new Node(11);
        // recursive
        System.out.println("==============recursive==============");
        System.out.print("pre-order: ");
        preOrderRecur(head);
        System.out.println();
        System.out.print("in-order: ");
        inOrderRecur(head);
        System.out.println();
        System.out.print("pos-order: ");
        posOrderRecur(head);
        System.out.println();

        // unrecursive
        System.out.println("============unrecursive=============");
        preOrderUnRecur(head);
        inOrderUnRecur(head);
        posOrderUnRecur1(head);
        posOrderUnRecur2(head);
        SequenceTraversal(head);
    }
    //preorder traversal先序遍历  recursive 递归的
    public static void preOrderRecur(Node head) {
        if(head==null){
            return;
        }
        System.out.print(head.value+" ");
        preOrderRecur(head.left);
        preOrderRecur(head.right);
    }
    //inorder traversal中序遍历
    public static void inOrderRecur(Node head) {
        if (head == null) {
            return;
        }
        inOrderRecur(head.left);
        System.out.print(head.value + " ");
        inOrderRecur(head.right);
    }
    //postorder traversal后序遍历
    public static void posOrderRecur(Node head) {
        if (head == null) {
            return;
        }
        posOrderRecur(head.left);
        posOrderRecur(head.right);
        System.out.print(head.value + " ");
    }
    public static void preOrderUnRecur(Node head) {
        //先右后左存入栈，弹出时打印
        System.out.print("pre-order: ");
        if (head!=null){
            Stack<Node> nodes = new Stack<>();
            nodes.push(head);
            while (!nodes.empty()){
                head=nodes.pop();
                System.out.print(head.value + " ");
                if(head.right!=null){
                    nodes.push(head.right);
                }
                if(head.left!=null){
                    nodes.push(head.left);
                }
            }
        }
        System.out.println();
    }
    public static void inOrderUnRecur(Node head) {
        //用null判断
        //先把左边界压入至null，然后如果是null，弹出栈顶，打印，将该元素的右孩子赋给变量继续循环
        System.out.print("in-order: ");
        if(head!=null){
            Stack<Node> nodes = new Stack<>();
            while (!nodes.empty()||head!=null){
                if(head!=null){
                    nodes.push(head);
                    head=head.left;
                }else {
                    head=nodes.pop();
                    System.out.print(head.value + " ");
                    head=head.right;
                }
            }
        }
        System.out.println();
    }
        public static void posOrderUnRecur1(Node head) {
        //用先左后右进栈，弹出存入收集栈 再弹出收集栈
        System.out.print("pos-order: ");
        if (head!=null){
            Stack<Node> nodes = new Stack<>();
            Stack<Node> collect = new Stack<>();
            nodes.push(head);
            while (!nodes.empty()){
                head=nodes.pop();
                collect.push(head);
                if(head.left!=null){
                    nodes.push(head.left);
                }
                if(head.right!=null){
                    nodes.push(head.right);
                }
            }
            var a = collect.iterator();
            while (a.hasNext()){
                System.out.print(collect.pop().value+" ");
            }
        }
        System.out.println();
    }
    public static void posOrderUnRecur2(Node head) {
        //用是否为左右子树判断
        //不用收集栈的后序遍历，先存入左边界，再peek 比较复杂
        System.out.print("pos-order: ");
        if (head != null) {
            Stack<Node> nodes = new Stack<>();
            nodes.push(head);
            Node c = null;
            while (!nodes.empty()){
                c = nodes.peek();
                if(c.left!=null&&head!=c.left&&head!=c.right){
                    //用于控制只将左边界传入 并且head!=c.left控制不去重复压栈 head!=c.right控制别理右子树
                    nodes.push(c.left);
                }else if(c.right!=null&&head!=c.right){
                    //当树从最左下方往上走时，如果有右子树则压栈，并且head!=c.right控制不去重复压栈
                    nodes.push(c.right);
                }else {
                    System.out.print(nodes.pop().value+" ");
                    head=c; //控制别再重复压栈
                }
            }
        }
        System.out.println();
    }
}
class Node{
    public int value;
    public Node left;
    public Node right;
    Node(int value){
        this.value = value;
    }
}

打印二叉树

将中序遍历倒过来，右头左，递归遍历的时候传入高度、符号、节点、长度。将长度填补为17位、右子树是'v'，左子树是'^'，高度作用：假如是第三层的节点，需要先打印2*17个空格。

package ZuoShen.Class05;

public class PrintBinaryTree {
    public static void printTree(Node head) {
        System.out.println("Binary Tree:");
        printInOrder(head, 0, "H", 17);
        System.out.println();
    }

    public static void printInOrder(Node head, int height, String to, int len) {
        if (head == null) {
            return;
        }
        printInOrder(head.right, height + 1, "v", len);
        String val = to + head.value + to;
        int lenM = val.length();
        int lenL = (len - lenM) / 2;
        int lenR = len - lenM - lenL;
        val = getSpace(lenL) + val + getSpace(lenR);
        System.out.println(getSpace(height * len) + val);
        printInOrder(head.left, height + 1, "^", len);
    }

    public static String getSpace(int num) {
        String space = " ";
        StringBuffer buf = new StringBuffer("");
        for (int i = 0; i < num; i++) {
            buf.append(space);
        }
        return buf.toString();
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(-222222222);
        head.right = new Node(3);
        head.left.left = new Node(Integer.MIN_VALUE);
        head.right.left = new Node(55555555);
        head.right.right = new Node(66);
        head.left.left.right = new Node(777);
        printTree(head);

        head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.right.left = new Node(5);
        head.right.right = new Node(6);
        head.left.left.right = new Node(7);
        printTree(head);

        head = new Node(1);
        head.left = new Node(1);
        head.right = new Node(1);
        head.left.left = new Node(1);
        head.right.left = new Node(1);
        head.right.right = new Node(1);
        head.left.left.right = new Node(1);
        printTree(head);
    }
}

宽度优先遍历（层序遍历）

用队列，先进先出，头进尾出，放入头结点，弹出然后打印，先进左再进右（如果有的话），出来的时候直接打印再先进左再进右。（类似于后序遍历装入收集栈的操作）

代码实现：

    public static void SequenceTraversal(Node head){
        //层序遍历
        Queue<Node> nodes = new LinkedList<>();
        if(head!=null){
            nodes.add(head);
            while (!nodes.isEmpty()){
                head = nodes.poll();
                System.out.print(head.value+" ");
                if(head.left!=null){
                    nodes.add(head.left);
                }
                if(head.right!=null){
                    nodes.add(head.right);
                }
            }
        }
        System.out.println();
    }

找到树的最大宽度

方法一：通过宽度优先遍历实现，其中有队列，利用一个map存储将节点作为Key，所在层数作为value，设置变量当前层数、当前节点数、最大宽度，每次poll出节点时判断该节点层数与当前层数是否一致，来决定更新。

方法二：不需要map，但是需要队列。

方法三：层序遍历

package ZuoShen.Class05;

import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;

public class TreeMaxWidth {
    public static void main(String[] args) {
        Node head = new Node(5);
        head.left = new Node(3);
        head.right = new Node(8);
        head.left.left = new Node(2);
        head.left.right = new Node(4);
        head.left.left.left = new Node(1);
        head.left.left.right = new Node(3);
        head.right.left = new Node(7);
        head.right.left.left = new Node(6);
        head.right.right = new Node(10);
        head.right.right.left = new Node(9);
        head.right.right.right = new Node(11);
        System.out.println(getMaxWidth1(head));
        System.out.println(getMaxWidth2(head));
        System.out.println(getMaxWidth3(head));
    }

    public static int getMaxWidth1(Node head){
        //方法一  用哈希表完成
        Queue<Node> nodes = new LinkedList<>();
        HashMap<Node,Integer> map = new HashMap<>();
        nodes.add(head);
        map.put(head,1);
        int curlevel = 1;
        int curNodeNum = 0;
        int max=Integer.MIN_VALUE;
        if(head!=null){
            while (!nodes.isEmpty()){
                head=nodes.poll();
                if(map.get(head)==curlevel){
                    curNodeNum++;
                }else {
                    max=Math.max(max,curNodeNum);
                    curNodeNum=1;
                    curlevel++;
                }
                if(head.left!=null){
                    nodes.add(head.left);
                    map.put(head.left,curlevel+1);
                }
                if(head.right!=null){
                    nodes.add(head.right);
                    map.put(head.right,curlevel+1);
                }
            }
        }
        return Math.max(max,curNodeNum);
    }
    public static int getMaxWidth2(Node head){
        //方法二：不用Hashmap只用队列，再加上max、curNode、head、curnum、curendNode四个变量
        Queue<Node> nodes = new LinkedList<>();
        nodes.add(head);
        Node curendNode = head;//当前层的最后一个
        Node curNode = null;   //当前节点
        int curnum = 0;//当前层数量
        int max = Integer.MIN_VALUE;
        while (!nodes.isEmpty()){
            head=nodes.poll();  //head用于遍历
            if(head.left!=null){
                nodes.add(head.left);
                curNode=head.left;  //curNode用于记录新进队列的节点
            }
            if(head.right!=null){
                nodes.add(head.right);
                curNode=head.right;
            }
            curnum++;
            if(head==curendNode){
                max=Math.max(max,curnum);
                curnum=0;
                curendNode=curNode; //将最新进入队列的节点作为当前层的尾部
                curNode=null;
            }
        }
        return max;
    }
    public static int getMaxWidth3(Node head){
        //方法三：层序遍历
        Queue<Node> nodes = new LinkedList<>();
        nodes.add(head);
        int max = Integer.MIN_VALUE;
        int curSize; //当前层的大小
        while (!nodes.isEmpty()){
            curSize=nodes.size();
            max=Math.max(max,curSize);
            for (int i = 0; i < curSize; i++) {//重点在于这个for循环次数为size大小，因此上一层的一定会被全部弹出
                head=nodes.poll();              //下一层的全部进入  然后重新计算size
                if(head.left!=null){
                    nodes.add(head.left);
                }
                if(head.right!=null){
                    nodes.add(head.right);
                }
            }
        }
        return max;
    }
}

p5:

排序算法的稳定性及其汇总

稳定性：相同值排序后的相对次序和排序之前一样。e.g.:先按照年龄排序，排序后按照班级排序，如果稳定，则班级内部有序。

• 选择排序是不稳定的。举例：[3,3,3,1,3,3]，会先把1和第一个3交换，那么前三个3的相对次序变化，不稳定。

• 冒泡排序稳定。因为相等的时候不去交换。

• 插入排序稳定。举例：[3,2,2]，0-0排序[3,2,2]，0-1排序[2,3,2],0-2排序先变成[2,2,3]这时第二个2与第一个2比较，相等不换

• 归并排序稳定。如果merge函数里面比较的时候，相等时先存入左侧的，稳定。小数和问题中先放右边的，不稳定。

• 快排不稳定。partition过程会与<区的前一个交换数字，这个过程会破坏稳定性。

• 堆排序不稳定。heapInsert就做不到，[5,4,4,6]中6会与第一个4交换。heapify也做不到。

• 计数排序和基数排序都稳定。思路上不一样，不需要比较，一个萝卜一个坑。

• 稳定与否不止看算法，还看实现，虽然归并能够达成稳定，但是如果实现不对还是会不稳定的。不稳定的是一定无法稳定。

• 时间空间稳定性总结：

  	时间复杂度	空间复杂度	稳定性
  选择排序	O(N2)	O(1)	✖
  冒泡排序	O(N2)	O(1)	✔
  插入排序	O(N2)	O(1)	✔
  归并排序	O(N*logN)	O(N)	✔
  快排(3.0)	O(N*logN)	O(logN)	✖
  堆排序	O(N*logN)	O(1)	✖

• 有一道题目，奇数放在数组左边，偶数放在数组右边，还要求原始的相对次序不变（要求时间O(N),空间O(1),稳定），碰到这个问题可怼面试官。该题目是快排的0,1问题的变种，但是快排不能实现稳定性，论文上可以实现但是空间会变成O(N)因此不行。

• 综合排序：工业界用的排序，先用快排进行分治递归，然后当样本量小到一定程度时进行插入排序，充分利用快排的基数划分以及分治和插入排序极低的常数项。

• java中Arrays.sort()，如果要排序的是基础类型，用快排，自己定义的类型，用归并。因为稳定性的关系。

• 第四节，排序内容结束，开始讲哈希表内容。

  • HashSet和HashMap底层实现原理一样，不过Set底层给了个默认值，其实都是Key-Value的。Set存取常数时间O(1)。
  • 放入哈希表的东西，如果是基础类型(包括String)，那么按值传递，如果是自定义的类对象，按地址传递，固定8字节。
  • TreeMap有序表，可以找到到第一个key，或者离某个key最近的key等类似操作。增删性能O(logn)。
  • 红黑树、AVL数、size-balace-tree和跳表都是有序表结构，只是底层具体实现不同。时间都是O(logn)。
  • 有序表存入的时候，如果是基础类型(包括String)，那么按值传递，如果是自定义的类对象，必须同时传入一个比较器不然会报错，内部按运用传递，内存占的是这个东西的内存大小。

链表

如果有换头结点的操作，那么需要有返回值，否则不需要。

反转单向和双向链表Redo

题目：分别实现反转单向链表和双向链表的函数

要求：如果链表长度为N，时间复杂度要求为O(N)，额外空间复杂度要求为O(1)

• 单链表的反转有两种，第一种是遍历，第二种是递归，代码如下：

  package ZuoShen;
  public class Linked_list {
      public static void main(String[] args) {
          Node node1 = new Node(1);
          Node node2 = new Node(2);
          Node node3 = new Node(3);
          Node node4 = new Node(4);
          node1.next = node2;
          node2.next = node3;
          node3.next = node4;
          Node temp = node1;
          while (temp.next!=null){
              System.out.println("value:"+temp.value + "next:" + temp.next.value);
              temp = temp.next;
          }
          temp = reverseSinglyList2(node1);
          System.out.println("----------");
          while (temp.next!=null){
              System.out.println("value:"+temp.value + "next:" + temp.next.value);
              temp = temp.next;
          }
      }
      //递归反转法
      public static Node reverseSinglyList2(Node head){
          if(head==null||head.next==null){//返回的head是最后一个有数的节点 前面的null是为了当只有一个节点的时候直接返回
              return head;
          }
          Node temp = head.next;  //temp作为head的下一个，用于回调时将指针指向head
          Node newHead = reverseSinglyList2(head.next); //保存新的头结点
          temp.next=head;    //更新指向
          head.next = null;  //更新指向
          return newHead;
      }
      //遍历反转法
      public static Node reverseSinglyList1(Node head){
          if(head==null){
              return null;
          }
          if(head.next==null){
              return head;
          }
          Node preNode = null;
          Node curNode = head;
          Node nextNode = null;
          while (curNode!=null){
              nextNode = curNode.next; //先保存下一个节点
              curNode.next = preNode;  //将现在的指向前一个
              preNode = curNode;   //将前一个挪到现在的  （指针已经完事，开始下一个）
              curNode = nextNode;  //然后将现在的往下走
          }
          return preNode;
      }
  }
  class Node{
      int value;
      Node next;
      Node(int value){
          this.value=value;
      }
  }
  

• 双链表和单链表很像，代码如下：

  package ZuoShen;
  
  public class Double_list {
      public static void main(String[] args) {
          DoubleNode doubleNode1 = new DoubleNode(1);
          DoubleNode doubleNode2 = new DoubleNode(2);
          DoubleNode doubleNode3 = new DoubleNode(3);
          doubleNode1.next=doubleNode2;doubleNode2.pre=doubleNode1;doubleNode2.next=doubleNode3;doubleNode3.pre=doubleNode2;
          printDoubleLinkedList(doubleNode1);
          DoubleNode temp = reverseList(doubleNode1);
          printDoubleLinkedList(temp);
      }
      public static void printDoubleLinkedList(DoubleNode head){
          System.out.print("Double Linked List: ");
          DoubleNode end = null;
          while (head != null) {
              System.out.print(head.value + " ");
              end = head;
              head = head.next;
          }
          System.out.print("| ");
          while (end != null) {
              System.out.print(end.value + " ");
              end = end.pre;
          }
          System.out.println();
      }
      public static DoubleNode reverseList(DoubleNode head){
          DoubleNode pre = null;
          DoubleNode next = null;
          while (head!=null){
              next = head.next;
              head.next = pre;
              head.pre = next;
              pre = head;
              head = next;
          }
          return pre;
      }
  }
  class DoubleNode{
      int value;
      DoubleNode next;
      DoubleNode pre;
      DoubleNode(int value){
          this.value=value;
      }
  }
  

打印两个有序链表的公共部分

题目：给定两个有序链表的头指针head1和head2，打印两个链表的公共部分。

要求：如果两个链表的长度之和为N，时间复杂度要求为O(N)，额外空间复杂度要求为O(1)

思路：两个指针，很简单。

package ZuoShen;
public class printCommenPartInLinkedList {
    public static void main(String[] args) {
        Node node1 = new Node(2);
        node1.next = new Node(3);
        node1.next.next = new Node(5);
        node1.next.next.next = new Node(6);
        Node node2 = new Node(1);
        node2.next = new Node(2);
        node2.next.next = new Node(5);
        node2.next.next.next = new Node(7);
        node2.next.next.next.next = new Node(8);
        Linked_list.printLinkedList(node1);
        Linked_list.printLinkedList(node2);
        printCommonPart(node1, node2);
    }
    public static void printCommonPart(Node head1,Node head2) {
        while (head1!=null&&head2!=null){
            if(head1.value<head2.value){
                head1=head1.next;
            }else if(head1.value>head2.value){
                head2=head2.next;
            }else {
                System.out.println(head1.value);
                head1=head1.next;
                head2=head2.next;
            }
        }

    }
}

面试时链表题的方法论：

• 对于笔试，不用太在乎空间复杂度，一切为了时间复杂度。
• 对于面试，时间复杂度依然放在第一位，但是一定要找到空间最省的方法

重要技巧：

• 额外数据结构记录（哈希表等）
• 快慢指针

判断一个链表是否为回文结构Redo

题目：给定一个单链表的头节点head，请判断该链表是否为回文结构。

要求：如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度达到O(1)。

例子：1->2->1，返回true； 1->2->2->1，返回true；15->6->15，返回true； 1->2->3，返回false。比较的是节点而不仅仅是数字，1->20->1是回文。

方法一：笔试情况，直接从头到尾遍历，依次放入栈中，然后再从头开始比较。需要额外空间O(N)。

方法二：用快慢指针，找到中点，只把右侧的节点放入栈中，再从头开始比较。需要额外空间O(N/2)。

方法三：面试情况，用快慢指针，找到中点，再往右侧走时，将右侧所有节点逆序，走到尾部的时候再从尾部开始走，依次与从头开始走的比较，在返回ture或false之前要将链表还原成原来的样子。需要额外空间O(1)。

package ZuoShen;
import java.util.Stack;
import static ZuoShen.Linked_list.printLinkedList;
public class IsPalindromeList {
    public static void main(String[] args) {
        Node head = null;
        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        head.next.next.next = new Node(2);
        head.next.next.next.next = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        System.out.print(isPalindrome2(head) + " | ");
        System.out.println(isPalindrome3(head) + " | ");
    }
    //方法一   需要O(n)的额外存储空间
    public static boolean isPalindrome1(Node head) {
        Stack<Node> nodes = new Stack<>();
        Node temp = head;
        while (temp!=null){
            nodes.push(temp);
            temp = temp.next;
        }
        temp = head;
        while (temp!=null){
            if(temp.value!=nodes.pop().value){
                return false;
            }
            temp = temp.next;
        }
        return true;
    }
    //方法二   需要O(n/2)的额外存储空间
    public static boolean isPalindrome2(Node head) {
        if (head == null || head.next == null) {
            return true;
        }
        Node fast = head;
        Node slow = head;
        while (fast!=null){
            if(fast.next!=null&&fast.next.next==null){
                fast=fast.next;//说明链表为偶数长度，且slow在对称轴的前一个
            }
            if(fast.next==null){
                break;  //说明链表为奇数长度，且slow在对称轴
            }
            fast=fast.next.next;
            slow=slow.next;
        }
        Node mid = slow.next;
        Stack<Node> nodes = new Stack<>();
        while (mid!=null){
            nodes.push(mid);
            mid=mid.next;
        }
        while (!nodes.isEmpty()){
            if(head.value!=nodes.pop().value){
                return false;
            }
            head=head.next;
        }
        return true;
    }
    //方法三   需要O(1)的额外存储空间
    public static boolean isPalindrome3(Node head) {
        if (head == null || head.next == null) {
            return true;
        }
        Node fast = head;
        Node slow = head;
        while (fast!=null){
            if(fast.next!=null&&fast.next.next==null){
                fast=fast.next;//说明链表为偶数长度，且slow在对称轴的前一个
            }
            if(fast.next==null){
                break;  //说明链表为奇数长度，且slow在对称轴
            }
            fast=fast.next.next;
            slow=slow.next;
        }
        //从mid开始  对后面的进行逆序操作
        Node mid = slow.next;
        Node temp = mid;
        Node next = null;
        Node pre = null;
        while (mid!=null){
            next=mid.next;
            mid.next=pre;
            pre=mid;
            mid=next;
        }
        //此时pre为右侧的头,将其和head开始比较
        while (pre!=null){
            if(pre.value!= head.value){
                return false;
            }
            pre=pre.next;
            head=head.next;
        }
        return true;
    }
}

将单向链表按某值划分成左边小、中间相等、右边大的形式Redo

题目：给定一个单链表的头节点head，节点的值类型是整型，再给定一个整 数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的 节点，中间部分都是值等于pivot的节点，右部分都是值大于pivot的节点。

进阶：在实现原问题功能的基础上增加如下的要求

• 调整后所有小于pivot的节点之间的相对顺序和调整前一样
• 调整后所有等于pivot的节点之间的相对顺序和调整前一样
• 调整后所有大于pivot的节点之间的相对顺序和调整前一样
• 时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

方法一（笔试）：直接搞个数组，把链表中的元素放入数组里，然后对数组进行partition，再把数组转成链表。但数组中无法做到相对次序不变。

方法二（面试）：设置6个指针，小于区域的头SH,小于区域的尾ST,一开始都为null，当遇到第一个小于pivot的节点时，头尾都变成该节点，当遇到第二个时，将第一个节点的next赋值为第二个节点，然后把ST指向第二个节点，以此类推。直到结束，将ST连向EH，将ET连向BH，完成。

package ZuoShen.Class04;
import java.util.Arrays;
import static ZuoShen.Class04.Linked_list.printLinkedList;
public class SmallerEqualBigger {
    public static void main(String[] args) {
        Node head1 = new Node(7);
        head1.next = new Node(9);
        head1.next.next = new Node(1);
        head1.next.next.next = new Node(8);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(2);
        head1.next.next.next.next.next.next = new Node(5);
        printLinkedList(head1);
        head1 = listPartition2(head1,5);
        printLinkedList(head1);
    }
    //方法一 笔试方法
    public static Node listPartition1(Node head, int pivot) {
        if (head == null) {
            return head;
        }
        int length = 0;
        Node temp = head;
        while (temp!=null){
            length++;
            temp=temp.next;
        }
        temp=head;
        Node[] nodes = new Node[length];
        int i = 0;
        for (; i < length; i++) {
            nodes[i] = temp;
            temp=temp.next;
        }
        //partition部分
        int left = 0;
        int right = length-1;
        for ( i = 0; i !=right; ) { //这里  i要和right比较而不是length！！
            if(nodes[i].value<pivot){
                swap(nodes,left,i);
                i++;
                left++;
            }else if(nodes[i].value>pivot){
                swap(nodes,right,i);
                right--;
            }else {
                i++;
            }
        }
        //将数组转成链表
        for ( i = 1; i != length; i++) {
            nodes[i-1].next=nodes[i];
        }
        nodes[i - 1].next = null;
        return nodes[0];
    }
    //方法二 面试方法
    public static Node listPartition2(Node head, int pivot) {
        Node sH = null;
        Node sT = null;
        Node eH = null;
        Node eT = null;
        Node bH = null;
        Node bT = null;
        Node next = null;
        Node temp = head;
        while (temp!=null){
            //此处需要断开节点之间原来的联系 很重要！！
            next = temp.next;
            temp.next=null;
            if(temp.value<pivot){
                if(sH==null){
                    sH=temp;
                    sT=temp;
                }else {
                    //该写给sH串值，然后sT指向temp
                    sT.next=temp;
                    sT = temp;
                }
            }else if(temp.value==pivot){
                if(eH==null){
                    eH=temp;
                    eT=temp;
                }else {
                    //该写给sH串值，然后sT指向temp
                    eT.next=temp;
                    eT = temp;
                }
            }else {
                if(bH==null){
                    bH=temp;
                    bT=temp;
                }else {
                    //该写给sH串值，然后sT指向temp
                    bT.next=temp;
                    bT = temp;
                }
            }
            temp=next;
        }
        //sT连eH，eT连bH
//        sT.next=eH;
//        eT.next=bH;
        //我的代码没有判断当st、eT为null时的情况,当null.next时会报错
        if(sT!=null){
            sT.next=eH;
            eT= eT==null?sT:eT; //eT==null的时候说明eH也是null，因此sT.next此时指向null
                                //eT!=null时，说明此时链表尾部是eT
        }
        if(eT!=null){
            eT.next=bH;    //然后如果bH是null的话，无所谓，bH不是的话连上第三个链
        }
        //以上情况中唯独没判断sT==null的情况，在return里面讲的
        //如果sH==null，则sT==null，此时进入第一个:后面，如果eH还是null，返回bH，否则返回eH，因为eT和bH一定是连着的
        return sH!=null?sH:eH!=null?eH:bH; //通过返回eH完成逆序
    }
    public static void swap(Node[] arr, int i, int j) {
        Node tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

复制含有随机指针节点的链表

题目：一种特殊的单链表节点类描述如下

class Node { 
    int value; 
    Node next; 
    Node rand; 
    Node(int val) {
        value = val; 
    } 
}

rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节 点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点 head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。

方法一：直接遍历一遍，然后将每个节点和它的复制放入map的key和value中，然后rand指针直接指向value即可

方法二：直接遍历一遍，然后赋值当前节点让其成为该节点的next，然后与map中类似的一一对应关系。

package ZuoShen.Class04;
import java.util.HashMap;
import java.util.Map;
public class CopyListWithRandom {
    public static void main(String[] args) {
        Node head = null;
        Node res1 = null;
        Node res2 = null;
        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        head.next.next.next = new Node(4);
        head.next.next.next.next = new Node(5);
        head.next.next.next.next.next = new Node(6);
        head.rand = head.next.next.next.next.next; // 1 -> 6
        head.next.rand = head.next.next.next.next.next; // 2 -> 6
        head.next.next.rand = head.next.next.next.next; // 3 -> 5
        head.next.next.next.rand = head.next.next; // 4 -> 3
        head.next.next.next.next.rand = null; // 5 -> null
        head.next.next.next.next.next.rand = head.next.next.next; // 6 -> 4
        printRandLinkedList(head);
        res1 = copyListWithRand1(head);
	    printRandLinkedList(res1);
        res2 = copyListWithRand2(head);
        printRandLinkedList(res2);
        printRandLinkedList(head);
        System.out.println("=========================");

    }
    //方法一
    public static Node copyListWithRand1(Node head) {
        HashMap<Node,Node> nodeNodeMap = new HashMap<>();
        Node cur = head;
        while (cur!=null){
            nodeNodeMap.put(cur,new Node(cur.value));
            cur=cur.next;
        }
        cur=head;
        while (cur!=null){
            nodeNodeMap.get(cur).next=nodeNodeMap.get(cur.next);
            nodeNodeMap.get(cur).rand=nodeNodeMap.get(cur.rand);
            cur=cur.next;
        }
        return nodeNodeMap.get(head);
    }
    //方法二
    public static Node copyListWithRand2(Node head) {
        Node cur = head;
        //复制这些节点
        while (cur!=null){
            Node temp = new Node(cur.value);
            temp.next= cur.next;
            cur.next=temp;
            cur=temp.next;
        }
        cur=head;
        //绑定rand
        //因为复制了一份所以一定是偶数
        while (cur!=null) {
            //直接赋值rand.next有可能rand是null而导致空指针
            cur.next.rand=cur.rand==null?null:cur.rand.next;
            cur=cur.next.next;
        }
        cur=head;
        Node head2 = cur.next;
        Node a = cur.next;
        //split这两个链表
        while (cur.next.next!=null) {
            cur.next=head2.next;
            cur=head2.next;
            head2.next=cur.next;
            head2=cur.next;
        }
        cur.next=null;
        return a;
    }
    public static void printRandLinkedList(Node head) {
        Node cur = head;
        System.out.print("order: ");
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.next;
        }
        System.out.println();
        cur = head;
        System.out.print("rand:  ");
        while (cur != null) {
            System.out.print(cur.rand == null ? "- " : cur.rand.value + " ");
            cur = cur.next;
        }
        System.out.println();
    }
    public static class Node {
        public int value;
        public Node next;
        public Node rand;
        public Node(int data) {
            this.value = data;
        }
    }
}

要求：时间复杂度O(N)，额外空间复杂度O(1)。

p4:

堆排序

1. ：时间复杂度O(N*logN)，额外空间复杂度O(1)。

   • 完全二叉树 叶子节点个数：N/2 倒数第二层节点数：N/4 。

     T(N) = N/2 1 + N/4 * 2 + N/8 * 3 + N/16 * 4 +.... 用2T(N)-T(N) 作为相减 得T(N) = N + N/2 +N/4 +N/8 + ... 等比求和logN

   • 假设将数组从0~6排成完全二叉树，第一层是0，第二程1，2；第三层3，4，5，6。假设坐标是i,则左孩子是2i+1，右孩子是2i+2，父节点为(i-1)/2。

   • 大根堆：每个父节点都是它子树的最大值。

   • heapinsert：新进入的元素都要去跟自己的父元素比较，如果大，就交换。时间复杂度和高度一致，O(logN)。

   • heapify:取出最大值时，将最后一个元素放到根节点，然后将heapSize-1，将父节点与左右孩子比较，大的放在父节点，然后周而复始。时间复杂度和高度一致，O(logN)。

   • 如果改变了堆中的一个值，先heapinsert然后heapify无脑完事。

   • 堆排序：先从数组中依次读入，每读入一个数进行heapinsert，heapSize++。然后取出最大值和最后一个位置交换，heapSize--，然后heapify，然后重复。

   • 优先级队列结构就是，堆结构 ，在java中为PriorityQueue，认为堆顶是优先级最大的。初始化的时候默认大小是11，扩容每次扩容1.5倍( 旧容量小于64时 直接翻倍 否则容量增加50%)。假设16个元素，扩容2倍，初始2个，那么扩容3次，因此扩容次数为logN，但是由于扩容的时候要复制N个元素，因此总的扩容代价为N*logN，平均到每个元素上扩容代价就是logN的。

   • 分情况使用系统提供的PriorityQueue，因为无法高效的修改堆的值再进行heapify，如果有这种对黑盒的操作，那么得自己手动实现堆，如果没有，可以用系统中的PriorityQueue。

堆排序代码

package com.ldl.test;

import java.util.*;

public class test  {
    public static void main(String[] args) {
//        System.out.println(Arrays.toString(new test().nextGreaterElement(new int[]{4,1,2},new int[]{1,3,4,2})));
        int[] temp = new int[]{4,2,0,3,2,5};
        new test().heapSort(temp);
    }

    public void heapSort(int[] arr){
        //第一步 先构建大顶堆
        for (int i = 0; i < arr.length; i++) {
            // 插入节点 并让这个节点找到自己应该在的位置
            heapInsert(arr,i);
        }
        //第二步 拆分大顶堆 升序输出
        //这时已经成为大顶堆了  最大值应当放在最后 从头开始
        int heapSize = arr.length-1;
        for(int i=arr.length-1;i>=0;i--){
            //从尾部开始 和大顶堆的头交换
            swap(arr,0,i);
            //交换后堆的大小-1，并重新让堆有序
            heapify(arr,0,--heapSize);
        }
        System.out.println(Arrays.toString(arr));
    }
    //让最小值从大顶堆的头上走到自己合适的位置
    private void heapify(int[] arr,int index,int size){
        int left = index*2+1;
        int right = index*2+2;
        int max = index;
        if(left<size&&arr[left]>arr[max]){
            max=left;
        }
        if(right<size&&arr[right]>arr[max]){
            max=right;
        }
        //小于左右孩子的话 交换更大的孩子上来  自己去到max位置 继续递归往下走
        if(index!=max){
            swap(arr,index,max);
            heapify(arr,max,size);
        }
    }
    private void heapInsert(int[] arr,int index){
        //新插入的节点比父节点大的话要一直往上交换
        //走到最上面的时候会在0处和自己相等 结束循环
        while (arr[index]>arr[(index-1)/2]){
            swap(arr,index,(index-1)/2);
            index = (index-1)/2;
        }
    }

    private void swap(int[] arr,int a,int b){
        arr[a]=arr[a]^arr[b];
        arr[b]=arr[a]^arr[b];
        arr[a]=arr[a]^arr[b];
    }

}

堆排序扩展题目

题目描述：已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素的移动距离可以不超过k，并且k相对于整个数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。

思路：搞一个大小为k的小根堆，heapify完后将0位置上的元素放入数组的第一个，因为每个元素排序不可能超过k，因此数组的第一个元素即最小值一定在这个小根堆里。然后放入第k+1个元素，heapify，取出第一个放入第二个位置，以此类推。当数组中剩余位置正好为小根堆大小时，将小根堆中的数从小到大排入即可，因此时间复杂度为O(N*logK)，k足够小时甚至可以认为是O(N).

public static void sortedArrDistanceLessK(int[] arr,int k){
        //默认是小根堆
        PriorityQueue<Integer> heap = new PriorityQueue<>();
        //index表示堆尾端数字在数组中的脚标
        int index=0;
        for (; index <= k; index++) {
            heap.add(arr[index]);
        }
        //i代表小根堆中要放入数组时对应数组的脚标
        int i=0;
        for(;index<arr.length;i++,index++){
            arr[i] = heap.poll();
            heap.add(arr[index]);
        }
        while (!heap.isEmpty()){
            arr[i++] = heap.poll();
        }
    }

桶排序

1. 桶排序思想下的排序都是不基于比较的排序
2. 时间复杂度为O(N)，额外空间复杂度O(M)
3. 应用范围有限，需要样本的数据状况满足桶的划分

常见的两种桶排序：

• 计数排序

  比较员工年龄，按照年龄排序，可以创建一个0-200的记录频率，然后将每个位置上出现的次数++，然后将这些排列。

• 基数排序

  数字比较，现有十个桶，假设用队列实现桶，先用个位排序，从左边的桶先进先出，然后十位，然后百位。

  优化版本：首先有一个count数组，大小为10，第一次记录个位上的数字都是多少数量，但是记录的是累加和，然后arr数组中的元素从右往左走，第一个元素的个位上是a，就去找，在count[a]，在该基础上-1，并放入辅助数组中，遍历完成后，将辅助数组放入arr，第一遍完成，去看10位上的数字排序。这样的好处是，在count处用累加和，可以实现一定程度的分片。

  例如：数组[013,021,011,052,062],count[0,0,0,0,0,0,0,0,0,0],求完数量后为count:[0,2,2,1,0,0,0,0,0,0],求完累加和：count：[0,2,4,5,5,5,5,5,5,5], 准备工作完成。开始放入临时数组bucket，首先从右往左看arr中第一个元素，062，个位数是2，此时

  count[2]为4，因此062放入bucket[3]中，count[2]--，此时count为[0,2,3,5,5,5,5,5,5,5], 依次类推，完成个位的桶排序。

  package ZuoShen;
  import java.util.Arrays;
  public class radix_sort {
      public static void main(String[] args) {
          int[] arr = {6,900,4000,32,11,312,328,91,10};
          radixSort(arr);
          System.out.println(Arrays.toString(arr));
      }
      public static void radixSort(int[] arr){
          if(arr==null||arr.length<2){
              return;
          }
          radixSort(arr,0,arr.length-1,maxbits(arr));
      }
      //桶排序
      public static void radixSort(int[] arr,int L,int R,int digit){
          final int radix = 10;//桶是0-9，这个永远不会变，十进制只有10个数
          int i = 0,j = 0;
          int[] bucket = new int[R-L+1];//有多少个数就创建多少的辅助空间
          for(int d=0;d<digit;d++){//有多少位就要进出几次
              int[] count = new int[radix];//代表，该位上的数字数量的累加和  length=10
              for(i=L;i<=R;i++){
                  j=getDigit(arr[i],d);  //返回i元素第d位上的数字
                  count[j]++;  //记录d位上位j的元素数量   等价于初始的桶排序版本
              }
              for ( i = 1; i < radix; i++) {
                  count[i] = count[i]+count[i-1]; //优化后，计算count累加和
              }
              for(i=R;i>=L;i--){          //相当于一次出桶操作
                  j=getDigit(arr[i],d);
                  bucket[count[j]-1] = arr[i]; //从右往左开始，判断该元素d位置数字，将其放到辅助数组中
                  count[j]--;                  //位置为count数组中，以该元素d位置数字为脚标的元素-1
              }
              for(i=L,j=0;i<=R;i++,j++){
                  arr[i] = bucket[j];  //将辅助数组赋值到arr中对应位置上
              }
          }
      }
      //用于返回第d位上的数字
      public static int getDigit(int x,int d){
          return ((x / ((int) Math.pow(10,d)))%10); //pow() 方法用于返回第一个参数的第二个参数次方。
      }
      //这个数组中最大值有多少位
      public static int maxbits(int[] arr){
          int max = Integer.MIN_VALUE;
          for (int i = 0; i < arr.length; i++) {
              max = Math.max(max,arr[i]);
          }
          int res = 0;
          while (max!=0){
              max/= 10;
              res++;
          }
          return res;
      }
  }
  

p3:

1. mid=(L+R)/2 可能会溢出；改成 mid=L+(L-R)/2；提升效率，改成mid=L+(R-L)>>1。

2. Master公式：T(N) = aT(N/b) + O(N^d)。

   其中：a代表子规模执行次数，b代表子规模大小，d代表除了子规模调用其他的操作的时间复杂度。

   • 若log_ba<d ，时间复杂度为 O(N^d)
   • 若log_ba>d ，时间复杂度为 O(N^log_ba)
   • 若log_ba==d ，时间复杂度为 O(N^b * logN)

归并排序

复习链接：https://www.cnblogs.com/chengxiao/p/6194356.html

• 整体就是一个简单递归，左边排好序、右边排好序，让其整体有序。

• 让其整体有序的过程用了外排序方法。

• 利用master公式来求解时间复杂度。

• 归并排序比另外三个（插入、查找、冒泡）优秀的实质（没有浪费比较，每一轮比较都将结果留存下来了顺序的一个部分数组，不遗漏不重算）。

  时间复杂度O(N*logN)，额外空间复杂度O(N)

  不遗漏不重算：举例数组[a,b,c,d,e,f,g]，以c为例子，a,b先比成为[a,b]，然后与c相比合并成[..c..]的一个数组，接下来c依次合并，并与下面的未知继续比较合并，每个都只比较一次。

  为什么归并排序过程中能实现单方向的大小判断？实际上是因为归并排序在排序过程中保持了数据的局部有序性，当合并时，在两个子数组整体之间存在相对位置关系。这也是为什么只有在合并的时候才能进行单方向上的大小判断。

  归并算法代码

  package ZuoShen;
  import java.lang.reflect.Array;
  import java.util.Arrays;
  //归并排序
  public class merge_sort {
      public static void main(String[] args) {
          int[] arr = {1,3,2,4,5};
          mergesort(arr,0,arr.length-1);
          System.out.println(Arrays.toString(arr));
      }
      public static void mergesort(int[] arr,int L,int R){
          if(L==R){
              return;
          }
          int mid = L + ((R-L)>>1);
          mergesort(arr,L,mid);
          mergesort(arr,mid+1,R);
          merge(arr,L,mid,R);
      }
      public static  void  merge(int[] arr,int L,int M,int R){
          int[] help = new int[R-L+1];
          int i=0;
          int p1=L;
          int p2=M+1;
          while (p1<=M&&p2<=R){
              help[i++]=arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];
          }
          while (p1<=M){
              help[i++]=arr[p1++];
          }
          while (p2<=R){
              help[i++]=arr[p2++];
          }
          for (i  = 0; i < help.length; i++) {
              arr[L+i]= help[i];
              
              
          }
      }
  }
  

小数和问题Redo（分治策略）

问题描述：小和问题和逆序对问题 小和问题 在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组 的小和。求一个数组 的小和。 例子:[1,3,4,2,5] 1左边比1小的数，没有; 3左边比3小的数，1; 4左 边比4小的数，1、3; 2左边比2小的数，1; 5左边比5小的数，1、3、4、 2; 所以小和为1+1+3+1+1+3+4+2=16。

思路：将求左边比自己小的数转换为求右边比自己大的数的数量，再乘上本身，加给结果。

package ZuoShen;
public class merge_sort {
    public static void main(String[] args) {
        int[] arr = {1,3,2,4,5};//小数和18
        System.out.println(smallSum(arr));
    }
    public static int smallSum(int[] arr){
        if(arr==null||arr.length<2){
            return 0;
        }
        return process(arr,0,arr.length-1);
    }

    public static int process(int[] arr,int L,int R){
        if(L==R){
            return 0;
        }
        int mid = L + ((R-L)>>1);
        return process(arr,L,mid)+ process(arr,mid+1,R)+ merge(arr,L,mid,R);//这里返回的只有最后一次的合并 也就是想要的结果  中间的过程都是不要的
    }
    public static  int  merge(int[] arr,int L,int M,int R){
        int[] help = new int[R-L+1];
        int i=0;
        int p1=L;
        int p2=M+1;
        int res=0;
        while (p1<=M&&p2<=R){
            res += arr[p1]<arr[p2]?arr[p1]*(R-p2+1):0;
            help[i++]=arr[p1]<arr[p2]?arr[p1++]:arr[p2++];
        }
        while (p1<=M){
            help[i++]=arr[p1++];
        }
        while (p2<=R){
            help[i++]=arr[p2++];
        }
        for (i  = 0; i < help.length; i++) {
            arr[L+i]= help[i];
        }
        return res;
    }
}

逆序对问题

问题描述：数组中的两个数，若前面的一个数大于后面的一个数，那么这两个数组成一个逆序对。输入一个数组，返回逆序对的个数。

package ZuoShen.Class04;


import java.util.HashMap;
import java.util.Map;

public class merge_sort {
//    public static void main(String[] args) {
//        HashMap<Integer,Node> map = new HashMap<>();
//        Node a = new Node(1);
//        Node b = new Node(2);
//        map.put(1,a);
//        a.value=2;
//        System.out.println(map.get(1).value);
//    }
    public static void main(String[] args) {
        int[] arr = {1,3,2,3,1};//逆序对4
        System.out.println(smallSum(arr));
    }
    public static int smallSum(int[] arr){
        if(arr==null||arr.length<2){
            return 0;
        }
        return process(arr,0,arr.length-1);
    }

    public static int process(int[] arr,int L,int R){
        if(L==R){
            return 0;
        }
        int mid = L + ((R-L)>>1);
        return process(arr,L,mid)+ process(arr,mid+1,R)+ merge(arr,L,mid,R);
    }
    public static  int  merge(int[] arr,int L,int M,int R){
        int[] help = new int[R-L+1];
        int i=0;
        int p1=L;
        int p2=M+1;
        int res=0;
        while (p1<=M&&p2<=R){
            res += arr[p1]>arr[p2]?(M-p1+1):0;
            // 因为如果arr[p1]此时比右数组的当前元素arr[p2]大，
            // 那么左数组中arr[p1]后面的元素就都比arr[p2]大
            // 因为数组此时是有序数组
            help[i++]=arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];
        }
        while (p1<=M){
            help[i++]=arr[p1++];
        }
        while (p2<=R){
            help[i++]=arr[p2++];
        }
        for (i  = 0; i < help.length; i++) {
            arr[L+i]= help[i];
        }
        return res;
    }
}

快排

时间最差情况是O(N²),原因就是划分的位置太差了，即取得第一个或最后一个值。

空间最差是O(N)，最好和平均(收敛至)是O(logN),要记录基数(划分值)位置。

挖坑填数 + 分治法：举例｛7，5，9，4，1，3，10｝，取第一个数为基数，存到temp中，0位置上空出来，从后往前找第一个比temp小的数字，挖出来放到0位置上，这里是3，然后3位置空出来了，从前往后找比temp大的，这里是9，然后将9放入3位置上，9位置空了出来，从后往前找比7小的数，这里是1，然后从前往后找比temp大的，无了，左右指针相遇，将temp放入4位置。

• 1.0 直接交换 分成两部分，一部分是小于该数，另一部分是大于该数。

• 2.0 分成三部分，一部分是小于该数，一部分是等于该数，另一部分是大于该数。可以一次确定一批数。

• 3.0 每次选数之前，随机等概率选一个位置的数和最后一个数交换，然后再取最后一个数开始划分。这样复杂度为O(N*logN)

• 4.0 三数取中法，虽然随机基准数方法选取方式减少了出现不好分割的几率，但是最坏情况下还是 O(n²)。为了缓解这个尴尬的气氛，就引入了「三数取中」这样的基准数选取方式。

  快排1.0代码：

  package ZuoShen;
  
  import java.util.Arrays;
  
  public class quick_sort {
      public static void main(String[] args) {
          int[] arr = {6,5,1,8,9,8,4,5,1};
          quickSort(arr,0,arr.length-1);
          System.out.println(Arrays.toString(arr));
      }
      private static void quickSort(int[] arr, int left, int right) {
          if (arr == null || left >= right || arr.length <= 1)
              return;
          int mid = partition(arr, left, right);
          quickSort(arr, left, mid);
          quickSort(arr, mid + 1, right);
      }
      private static int partition(int[] arr, int left, int right) {
          int temp = arr[left];
          while (right > left) {
              // 先判断基准数和后面的数依次比较
              while (temp <= arr[right] && left < right) {
                  --right;
              }
              // 当基准数大于了 arr[right]，则填坑
              if (left < right) {
                  arr[left] = arr[right];
                  ++left;
              }
              // 现在是 arr[right] 需要填坑了
              while (temp >= arr[left] && left < right) {
                  ++left;
              }
              if (left < right) {
                  arr[right] = arr[left];
                  --right;
              }
          }
          arr[left] = temp;
          return left;
      }
  }
  

  快排3.0实现：随机取基数

  package ZuoShen;
  import java.util.Arrays;
  public class atest {
      public static void quickSort(int[] arr) {
          if (arr == null || arr.length < 2) {
              return;
          }
          quickSort(arr, 0, arr.length - 1);
      }
      public static void quickSort(int[] arr, int l, int r) {
          if (l < r) {
              swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
              int[] p = partition(arr, l, r);
              quickSort(arr, l, p[0] - 1);
              quickSort(arr, p[1] + 1, r);
          }
      }
      public static int[] partition(int[] arr, int l, int r) {
          int less = l - 1;
          int more = r;
          while (l < more) {
              if (arr[l] < arr[r]) {
                  swap(arr, ++less, l++);
              } else if (arr[l] > arr[r]) {
                  swap(arr, --more, l);
              } else {
                  l++;
              }
          }
          swap(arr, more, r);
          return new int[] { less + 1, more };
      }
      public static void swap(int[] arr, int i, int j) {
          int tmp = arr[i];
          arr[i] = arr[j];
          arr[j] = tmp;
      }
      // for test
      public static void comparator(int[] arr) {
          Arrays.sort(arr);
      }
      // for test
      public static int[] generateRandomArray(int maxSize, int maxValue) {
          int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
          for (int i = 0; i < arr.length; i++) {
              arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
          }
          return arr;
      }
      // for test
      public static int[] copyArray(int[] arr) {
          if (arr == null) {
              return null;
          }
          int[] res = new int[arr.length];
          for (int i = 0; i < arr.length; i++) {
              res[i] = arr[i];
          }
          return res;
      }
      // for test
      public static boolean isEqual(int[] arr1, int[] arr2) {
          if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
              return false;
          }
          if (arr1 == null && arr2 == null) {
              return true;
          }
          if (arr1.length != arr2.length) {
              return false;
          }
          for (int i = 0; i < arr1.length; i++) {
              if (arr1[i] != arr2[i]) {
                  return false;
              }
          }
          return true;
      }
      // for test
      public static void printArray(int[] arr) {
          if (arr == null) {
              return;
          }
          for (int i = 0; i < arr.length; i++) {
              System.out.print(arr[i] + " ");
          }
          System.out.println();
      }
      // for test
      public static void main(String[] args) {
          int testTime = 500000;
          int maxSize = 100;
          int maxValue = 100;
          boolean succeed = true;
          for (int i = 0; i < testTime; i++) {
              int[] arr1 = generateRandomArray(maxSize, maxValue);
              int[] arr2 = copyArray(arr1);
              quickSort(arr1);
              comparator(arr2);
              if (!isEqual(arr1, arr2)) {
                  succeed = false;
                  printArray(arr1);
                  printArray(arr2);
                  break;
              }
          }
          System.out.println(succeed ? "Nice!" : "Fucking fucked!");
          int[] arr = generateRandomArray(maxSize, maxValue);
          printArray(arr);
          quickSort(arr);
          printArray(arr);
  
      }
  }
  

  快排4.0实现：仅替换上方代码的partition部分

  private static int partition(int[] arr, int left, int right) {
          // 采用三数中值分割法
          int mid = left + (right - left) / 2;
          // 保证左端较小
          if (arr[left] > arr[right])
              swap(arr, left, right);
          // 保证中间较小
          if (arr[mid] > arr[right])
              swap(arr, mid, right);
          // 保证中间最小，左右最大
          if (arr[mid] > arr[left])
              swap(arr, left, mid);
          int pivot = arr[left];
          while (right > left) {
              // 先判断基准数和后面的数依次比较
              while (pivot <= arr[right] && left < right) {
                  --right;
              }
              // 当基准数大于了 arr[right]，则填坑
              if (left < right) {
                  arr[left] = arr[right];
                  ++left;
              }
              // 现在是 arr[right] 需要填坑了
              while (pivot >= arr[left] && left < right) {
                  ++left;
              }
              if (left < right) {
                  arr[right] = arr[left];
                  --right;
              }
          }
          arr[left] = pivot;
          return left;
      }
  

1. 给定一个数组arr和一个数num，把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)。（相当于快排的一趟）

   package ZuoShen;
   import java.util.Arrays;
   public class quick_sort {
       public static void main(String[] args) {
           int[] arr = {1, 3,6,4,3,2,8,9};
           onequicsort(arr,5);
           System.out.println(Arrays.toString(arr));
       }
       public static void onequicsort(int[] arr,int num){
           if (arr == null || arr.length < 2) {
               return;
           }
           int p1=0;
           int p2=arr.length-1;
           int i=0;
           while (p1<p2) {
               if(arr[i]<=num){
                   swap(arr,i++,p1++);
               }else {
                   swap(arr,i,p2--);
               }
           }
       }
       public static void swap(int[] arr, int L, int R) {
           int temp = arr[L];
           arr[L] = arr[R];
           arr[R] = temp;
       }
   }
   

荷兰国旗问题

(上面问题中条件添加，将等于num的放在数组中间)：

package ZuoShen;
import java.util.Arrays;
public class quick_sort {
    public static void main(String[] args) {
        int[] arr = {6,5,1,8,9,8,4,5,1};
        onequicsort(arr,5);
        System.out.println(Arrays.toString(arr));
    }
    public static void onequicsort(int[] arr,int num){
        if (arr == null || arr.length < 2) {
            return;
        }
        int p1=0;
        int p2=arr.length-1;
        int i=0;
        while (p1<p2-1) {
            if(arr[i]<num){
                swap(arr,i++,p1++);
            }else if(arr[i]>num){
                swap(arr,i,p2--);
            }else {
                i++;
            }
        }
    }
    public static void swap(int[] arr, int L, int R) {
        int temp = arr[L];
        arr[L] = arr[R];
        arr[R] = temp;
    }
}

p2:

1. 选择排序和冒泡排序

   选择排序是O(n²)，每次选取最大的，放在最前面，然后下次从第二个开始找到最后一个。

   冒泡也是O(n²)，一直交换到最后。

2. 插入排序

   插入排序最坏是O(n²)，最好是O(n)，但是算法一般都是按照最坏的来。插入是先排序0-1，然后0-2，然后0-3，eq.:排序0-5时，0-4已经排序好了，只需要将第五个数字插入即可，依次与4 3 2 1 判断并交换到对应位置上。

二进制加减乘除

通过位运算计算int的加减乘除:

加法原理:a+b

位的异或运算跟求'和'的结果一致：

异或 1^1=0 1^0=1 0^0=0

求和 1+1=0 1+0=1 0+0=0

位的与运算跟求'进位‘的结果一致：

位与 1&1=1 1&0=0 0&0=0

进位 1+1=1 1+0=0 0+0=0

所以a+b = (a^b)+((a&b)<<1)

减法原理:a-b

减去一个正数等于加上这个负数的补码.一个正数的补码是它的原码.一个负数的补码等于它的反码+1.即 -b = ~b+1.所以a-b = a+(-b) = a+ ~b+1.

补码的规定如下：

对正数来说，最高位为0，其余各位代表数值本身(以二进制表示)，如+42的补码为00101010。
对负数而言，把该数绝对值的补码按位取反，然后对整个数加1，即得该数的补码。如-42的补码为11010110(00101010按位取反11010101+1即11010110)

【例1】对 5 进行取反。

假设为16位。

5转换为二进制数为： 0000 0000 0000 0101得到二进制数

每一位取反： 1111 1111 1111 1010得到最终结果的补码

取补码： 1000 0000 0000 0110得到最终结果的原码

转换为十进制数：-6

则 5 取反为 -6 .

【例2】对 -5 进行取反。

假设为16位。

-5 转换为二进制数为： 1000 0000 0000 0101得到二进制数

取补码： 1111 1111 1111 1011得到二进制数的补码

每一位取反： 0000 0000 0000 0100 得到最终结果的补码

取补码： 0000 0000 0000 0100得到最终结果的原码

转换为十进制数：4

则 -5 取反为 4 .

如果用适合人类运算的计算方法：

如对 a 按位取反，则得到的结果为 -(a+1) .

此条运算方式对正数负数和零都适用。

所以_{（b-1）=-b可得a-b=a+（-b）=a+(}(b-1))。把减法转化为加法即可。

乘法原理:a*b

1.用循环加法替代乘法。a*b，就是把a累加b次。时间复杂度为O(N)。

2.在二进制数上做乘法.就是根据乘数的每一位为0或1时，将被乘数错位的加在积上。时间复杂度为O(logN)

除法原理:a/b

1.从被除数上减去除数，看能减多少次之后变得不够减。时间复杂度为O(N)。

2.采用类似二分法的思路，从除数*最大倍数开始测试，如果比被除数小，则要减去。下一回让除数的倍数减少为上一次倍数的一半，这样的直到倍数为1时，就能把被除数中所有的除数减去，并得到商。时间复杂度降低到O(logN)。

/**
     * 加法
     * @param a
     * @param b
     * @return
     */
    public static int add(int a,int b) {
        int res=a;
        int xor=a^b;//得到原位和
        int forward=(a&b)<<1;//得到进位和
        if(forward!=0){//若进位和不为0，则递归求原位和+进位和
            res=add(xor, forward);
        }else{
            res=xor;//若进位和为0，则此时原位和为所求和
        }
        return res;
    }
 
    /**
     * 减法
     * @param a
     * @param b
     * @return
     */
    public static int minus(int a,int b) {
        int B=~(b-1);
        return add(a, B);
    }
 
    /**
     * 乘法
     * @param a
     * @param b
     * @return
     */
    public static int multi(int a,int b){
        int i=0;
        int res=0;
        while(b!=0){//乘数为0则结束
            //处理乘数当前位
            if((b&1)==1){
                res+=(a<<i);
                b=b>>1;
                ++i;//i记录当前位是第几位
            }else{
                b=b>>1;
                ++i;
            }
        }
        return res;
    }
 
    /**
     * 除法
     * @param a
     * @param b
     * @return
     */
    public static int sub(int a,int b) {
        int res=-1;
        if(a<b){
            return 0;
        }else{
            res=sub(minus(a, b), b)+1;
        }
        return res;
    }
    public static void main(String[] args) {
        //加法运算
        int result1 = add(90,323);
        System.out.println(result1);
 
        //减法运算
        int result2 = minus(413,323);
        System.out.println(result2);
 
        int result3 = multi(90,2);
        System.out.println(result3);
 
        int result4 = sub(90,2);
        System.out.println(result4);
    }

异或的知识点

• 两个数字相异为1，相同为0，引申到int对比时，是32位的数字相异，也是相异为1，相同为0。

  public static void sway(int[] arr,int i,int j){
  	if(i!=j){
  		//不能两个值指向同一地址
  	    arr[i]=arr[i]^arr[j];
  	    arr[j]=arr[i]^arr[j];//就是arr[i]^arr[j]^arr[j]就表示a
  	    arr[i]=arr[i]^arr[j];//表示arr[i]^arr[j]^arr[i]^arr[j]^arr[j]就是b
      }
  }
  

• 可以理解为二进制上的不进位相加。

• 题目1：一组数只有一个数出现奇数次，其他出现偶数次，找出这个出现奇数次的数

  public class Main {
  	private static int process(int[] arr) {
  		int res = 0;
  		for (int i : arr) {
  			res ^= i;
  		}
  		return res;
  	}
  }
  

  取出最右边为1的二进制位所代表的数字

  int mostRightOne = pos & (~pos + 1); 
  // mostRightOne值在二进制位上的位次就是pos得最右第一个1的位置
  

• 题目2：有两种数出现了奇数次，另一种出现了偶数次，求出奇数次的a,b

  思路：先一路异或找到a^b，然后因为a!=b，因此一定有不相同的位，那取出两者从右边数第一个不相同的位置，即先取反+1再异或 （a^{b）。然后将与这个结果&运算==0的数字全部异或，也就获得了其中一个奇数次的数字，a或者b。在将其与a}b异或得到另一个数字。

  public class Main {
  	private static void process(int[] arr) {
  		int med = 0;
  		for (int a : arr) {
  			med ^= a;// 两个不同的单数^最后得到med
  		}
  		int rightOne = med & (~med + 1);// 取出med中二进制为1的位值（必存在，因为不同值）
  		int med1 = 0;
  		for (int a : arr) {
  			// 对应位为1的值取出进行^最后的到两个单数对应位为1的
  			// (a&rightOne)== 0得到对应位为0
  			if ((a & rightOne) == rightOne) {
  				med1 ^= a;
  			}
  		}
  		System.out.println(med1);// 两个单数其中一个值
  		System.out.println(med ^ med1);// 两个单数令一个值
  	}
  }
  

• 二分法的另类应用

  当数况和方法同时满足条件时，可以用二分法做。

  例如数组中相邻元素都不相等，而且要找到一个"局部最小点"，即即比左边小也比右边小的一个点。

  思路：根据数学定理，中间必有导数为0的点，取M为中点，如果不是"局部最小点"，则它左侧必有，一直向左边二分即可。