[模板] 插头 DP

[模板] 插头DP——从入门到入坟

陈丹琦——《基于连通性状态压缩的动态规划问题》

传送门

模板是插头DP的入门题，询问 带障碍网格中的合法回路个数。

概念类

棋盘模型问题：采用逐行，逐列，逐格的状态转移方式。

对于此题，逐格转移是最快的。

插头：整个 DP 中的核心。

定义

对于一个四联通问题来说，一个格子通常有上下左右四个插头，一个格子再一个方向上的插头定义为 该格子可以通过这个方向与外界连通。

比如说，插头 \(1\) 是上面黄底色格子的下插头，是下面格子的上插头。

如果逐行DP的话，第 \(i\) 行的所有下插头会成为第 \(i+1\) 行的所有上插头。

状态表示法

通过状态表示法，我们可以把轮廓线处的插头状态表示为一个 \(p\) 进制数。

最小表示法。

最小表示法，也就是用不同的数字来表示 轮廓线以上（已知部分） 不同的插头所处的线路。

比如上图轮廓线处状压起来就是 \((1,1,2,2)\)，至于最小表示类似于 字符串的最小表示，采用四进制存储以加快运算。

括号序列表示法。

对于一对连通的插头，用数对 \((1,2)\) 来表示，用 \(1\) 来代替左括号 \((\)，\(2\) 来代替右括号 \()\) 。

类似于括号序列，所以把它叫做括号序列表示法。

比如上图状压起来就是 \((1,2,1,2)\) 。

所有的状态表示法，都基于对线路的唯一表示，防止冲突。只要线路与状态表示一一对应，就可以是一种状态表示法。

轮廓线状压转移

通过状态表示法，根据轮廓线插头对当前格 \((i,j)\) 的影响 考虑几类可能的转移。

所谓轮廓线状压，也就是只关注轮廓线处的一些插头对逐格转移过程中当前格的影响。

根据格子所处位置附近连通块的连通情况，可以分为三类。

新建一个连通块。

当且仅当轮廓线处不存在向右或者向下的插头，\((i,j)\) 提供向下和向右的插头。

连接两个已有连通块。

轮廓线处有向右和向下的插头，\((i,j)\) 分别通过向左和向上的插头把它们连接起来。

接上之前的连通块。

也就是轮廓线处只有一个向右或向下的插头，\((i,j)\) 分别提供向左或向上的插头。

那么设 \(f(i,j,S)\) 表示当前处理完了 \((i,j)\) 及之前的点，轮廓线附近括号序列为 \(S\) 的方案数。

代码实现

采用滚动数组，对于一个 \((i,j)\) 维护一维 \(f\)。
用哈希表把 \(S\) 映射为序列数字，维护上一个点 \((i,j-1)\) 的所有状态信息，用挂链法处理哈希冲突。
采用刷表法，用哈希表维护 DP 过程。

上面讨论过了按照连通性分类，下面按照 \(up\) 和 \(left\) 插头的情况进行分类。

当前为障碍点，必须保证两个插头均为空才可加入决策集合。
当前不是障碍点。
1. 两个插头都没有：考虑新增一个连通块，括号序列改变。
2. 只有上面过来的插头：选择向右走或者向下走，注意：插头序列均改变。
3. 只有左面过来的插头：选择向右走或者向下走，插头序列均改变。
4. 上面和左面过来的插头都是 \(1\)，也就是都是左括号：向右找到第一个能和当前左括号匹配上的右括号的位置，计算插头贡献，插头序列改变。
5. 上面和左面过来的插头都是 \(2\)，也就是都是右括号：向左找到第一个能和当前右括号匹配上的左括号的位置，计算插头贡献，插头序列改变。
6. 上面过来的插头是 \(1\)，左面过来的插头是 \(2\)，直接连起来即可。
7. 上面过来的插头是 \(2\)，左面过来的插头是 \(1\)，说明形成了回路，在最后遍历到的非障碍点把答案加上，其它情况不管，这保证了最后一定是一种方案对应一条回路。

状压插头序列时的细节问题

对应于这一行：

for(int j=1;j<=tot[now];j++)a[now][j]<<=2;//详细分析

这就涉及到了当前 \(i\) 这一行的状压问题。

可以发现，一条竖线（ \((i,j)\) 左侧的边）将这一行分成了两部分，其中这一竖线占据第 \(j-1\) 位，这条竖线之前的第 \(t\) 列由于它都占据了第 \(t-1\) 位，而竖线右侧的第 \(t\) 列都占据了第 \(t\) 位。这是 \((i,j)\) 被刷到之前，也就是转移之前。

转移之后，竖线变为占据第 \(j\) 位，而之前的第 \(j\) 列占据了第 \(j-1\) 列，也就是说每次取到上面插头都是第 \(j\) 列，对于 上一行结束的状态序列，第 \(j\) 列表示的还是第 \(j-1\) 列，所以需要左移一位，这仅仅在每一行开始的时候做这个事情。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
	T x=0;char ch=getchar();bool fl=false;
	while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
	}
	return fl?-x:x;
}
const int maxn = 20 , P = 590027;
const int maxm = 6e5 + 10;
int n,m,mp[maxn][maxn],stx,sty;
#define LL long long
#define read() read<int>()
LL ans,f[2][maxm];
int head[maxm],tot[2],now,last;
int nxt[maxm],a[2][maxm];
int bit[28];
void Hash(int sta,LL val){//辅助维护上一阶段信息的哈希表
	int t=sta%P+1;
	for(int i=head[t];i;i=nxt[i]){
		if(a[now][i]==sta)return f[now][i]+=val,void();
	}
	nxt[++tot[now]]=head[t];head[t]=tot[now];
	a[now][tot[now]]=sta;f[now][tot[now]]=val;
}
void solve(){
	tot[now]=1;a[now][1]=0;f[now][1]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=tot[now];j++)a[now][j]<<=2;//详细分析
		for(int j=1;j<=m;j++){
			last=now;now^=1;tot[now]=0;
			memset(head,0,sizeof head);
			for(int k=1;k<=tot[last];k++){
				int sta=a[last][k],up=(sta>>(j*2))%4,left=(sta>>(j*2-2))%4;
				LL val=f[last][k];
				if(!mp[i][j]){if(!up && !left)Hash(sta,val);}//里面判不判都一样，保证合法即可
				else if(!up && !left){
					if(mp[i+1][j] && mp[i][j+1])Hash(sta+bit[j-1]+2*bit[j],val);//新开一个，1,0
				}
				else if(up && !left){
					if(mp[i+1][j])Hash(sta-bit[j]*up+bit[j-1]*up,val);//go down
					if(mp[i][j+1])Hash(sta-bit[j]*up+bit[j]*up,val);//go right
				}
				else if(!up && left){
					if(mp[i][j+1])Hash(sta-bit[j-1]*left+bit[j]*left,val);//go right
					if(mp[i+1][j])Hash(sta-bit[j-1]*left+bit[j-1]*left,val);//go down
				}
				else if(up==1 && left==1){//找到第一个匹配的右括号
					int sz=1;
					for(int t=j+1;t<=m;t++){
						if((sta>>(t*2))%4==1)sz++;
						if((sta>>(t*2))%4==2)sz--;
						if(!sz){
							Hash(sta-bit[j]-bit[j-1]-bit[t],val);//右括号->左括号
							break;
						}
					}
				}
				else if(up==2 && left==2){//找到第一个匹配的左括号
					int sz=1;
					for(int t=j-2;t>=0;t--){//t-1 --> t(真实)
						if((sta>>(t*2))%4==1)sz--;
						if((sta>>(t*2))%4==2)sz++;
						if(!sz){
							Hash(sta-2*bit[j]-2*bit[j-1]+bit[t],val);//左括号->右括号
							break;
						}
					}
				}
				else if(up==1 && left==2)Hash(sta-2*bit[j-1]-bit[j],val);
				else if(up==2 && left==1){
					if(i==stx && j==sty)ans+=val;
				}	
			}
		}
	}
}
char s[maxn];
int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++){
		cin>>s+1;
		for(int j=1;j<=m;j++){
			if(s[j]=='.')mp[i][j]=1,stx=i,sty=j;
			else if(s[j]=='*')mp[i][j]=0;
		}
	}
	bit[0]=1;
	for(int i=1;i<=12;i++)bit[i]=bit[i-1]<<2;
	solve();
	printf("%lld\n",ans);
	return 0;
}

简单例题

[SCOI2011]地板

题意

用 \(L\) 型地板铺满非障碍格子的方案数，\(L\) 型格子不能是条形的。

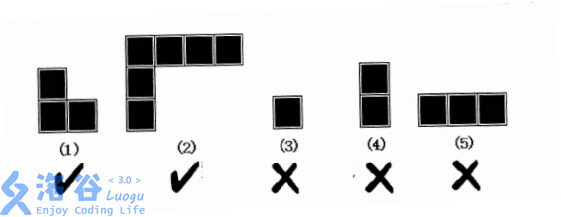
解题报告

类似于求回路的普通插头DP，有以下几点不同：

不需要使用上面的任何状态表示法，因为 不需要记录每一条线的连通情况 了。
由于一条 \(L\) 型地板只能拐一次弯，在插头处记录能不能拐弯。（\(1\) 表示可以拐弯，\(2\) 表示不能拐弯）
可以 在一条拐过弯的地板的任何时刻中止它，这也是最容易忘的。

新的体会（2021/8/6）

插头的真正含义是 相邻的两个格子可以连通，比如说中止当前地板时，就没有往外走的插头了。
三进制数在改状态改的少的情况下同样可以跑的飞快（除法对时间的影响小）。

换行时对于所有状态左移一位的操作，需要 分维计算。

for(int j=0;j<bit[m+1];j++)f[now^1][j]=0;
for(int j=0;j<bit[m];j++)f[now^1][j*3]=f[now][j];
now^=1;

否则会产生同一维之间的影响和一些奇怪错误。

插头DP真的是细节非常多，主要是分讨容易丢情况。

调试时的技巧

看当前结点可以由哪些状态转移过来，或者是与哪些插头相邻，手玩枚举这些所有可能的情况，看看丢没丢解。

cerr<<"pos: "<<i<<" "<<j<<" "<<s<<endl;//
cerr<<up<<" "<<left<<" "<<val<<endl;//

这是我调试时的图（第二个样例），明显对于 \((2,3)\) 这个点少了一种情况是：上插头为 \(1\)，这就是由于当时没有考虑停止当前地板的情况。

三进制写法：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
    T x=0;char ch=getchar();bool fl=false;
    while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
    while(isdigit(ch)){
        x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
    }
    return fl?-x:x;
}
const int P = 20110520;
inline void Plus(int &x,int y){
	x+=y;
	if(x>=P)x-=P;
}
const int maxm = 2e5 + 10;
const int maxn = 105;
int f[2][maxm],bit[100],mp[maxn][maxn];
char s[maxn];
int n,m,now,last;
void solve(){
	f[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<bit[m+1];j++)f[now^1][j]=0;
		for(int j=0;j<bit[m];j++)f[now^1][j*3]=f[now][j];
		now^=1;
		for(int j=1;j<=m;j++){
			last=now;now^=1;
			for(int s=0;s<bit[m+1];s++)f[now][s]=0;
			for(int s=0;s<bit[m+1];s++){
				if(!f[last][s])continue;
				int up=(s/bit[j])%3,left=(s/bit[j-1])%3;
				int val=f[last][s];
				if(!mp[i][j]){
					if(!up && !left)Plus(f[now][s],val);continue;
				}
				if(!up && !left){
					if(mp[i+1][j] && mp[i][j+1])Plus(f[now][s+2*bit[j]+2*bit[j-1]],val);
					if(mp[i+1][j])Plus(f[now][s+bit[j-1]],val);
					if(mp[i][j+1])Plus(f[now][s+bit[j]],val);
				}
				if(up && !left){
					if(up==1){
						if(mp[i][j+1])Plus(f[now][s-bit[j]+2*bit[j]],val);
					}
					if(up==2){
						Plus(f[now][s-2*bit[j]],val);
					}
					if(mp[i+1][j])Plus(f[now][s-up*bit[j]+up*bit[j-1]],val);
				}
				if(!up && left){
					if(left==1){
						if(mp[i+1][j])Plus(f[now][s-bit[j-1]+2*bit[j-1]],val);
					}
					if(left==2){
						Plus(f[now][s-2*bit[j-1]],val);
					}
					if(mp[i][j+1])Plus(f[now][s-left*bit[j-1]+left*bit[j]],val);
				}
				if(up==1 && left==1){
					Plus(f[now][s-bit[j]-bit[j-1]],val);
				}
			}
		}
	}
}
#define read() read<int>()
int main(){
	n=read();m=read();
	bool fl=(n<m);
	for(int i=1;i<=n;i++){
		cin>>s+1;
		for(int j=1;j<=m;j++){
			if(s[j]=='_')fl?(mp[j][i]=1):(mp[i][j]=1);
		}
	}
	if(fl)swap(n,m);
	bit[0]=1;
	for(int i=1;i<=m+1;i++)bit[i]=bit[i-1]*3;
	solve();
	printf("%d\n",f[now][0]);
	return 0;
}

posted @ 2021-08-12 18:32 ¶凉笙阅读(94) 评论(0) 编辑收藏举报

刷新页面返回顶部

¶凉笙