[模板] AC自动机
[模板] AC自动机
AC 自动机是以 Trie 树的结构 为基础,结合 KMP 的思想进行的一种多模式匹配算法。
典型应用是:用一个文本串来匹配多个模式串。
Trie 树构建
和 Trie 树模板没有区别,还是要记录模式串的结束位置。
放在 AC 自动机的算法里,一个结点表示一个字符串 \(S\) 的前缀,这也是这个模式串的一种状态。
严格意义来说,应该把 Trie 树的字符指针看成 边 比较形象。
失配指针 fail
类似与 KMP 中的 \(next\) 数组,我们把它们作下对比:
-
\(next\) 数组记录的是字符串 \(S\) 的一个前缀的 前缀等于后缀的最大长度 。
-
\(fail\) 指针指向 所有模式串的前缀中匹配当前状态的最长后缀。更加形象的说,\(fail\) 就是当前状态的一个后缀集合。
-
两者都是为了在失配的时候进行跳转用的。
构造思想 ,基本思想 。
设当前结点为 \(u\),\(p\) 为通过字符 \(c\) 指针的父亲,考虑如何构造 \(u\) 结点的失配指针。
-
如果 \(t[fail[p]][c]\) 存在,那么 \(fail[u]=t[fail[p][c]]\) ,类似于 KMP 中的继承 \(nxt\) 数组操作,这里是通过继承上一个状态而得到了延续状态的最长后缀。
-
如果上述结点不存在,向跳 \(next\) 数组一样跳 \(fail\),比如第二步就要找 \(t[fail[fail[p]]][c]\),直到找到存在结点或者到达根节点 \(rt=0\) 为止。
具体实现就是一直跳 \(fail\),直到存在该结点为止。

放一张 \(oi-wiki\) 的图理解一下:
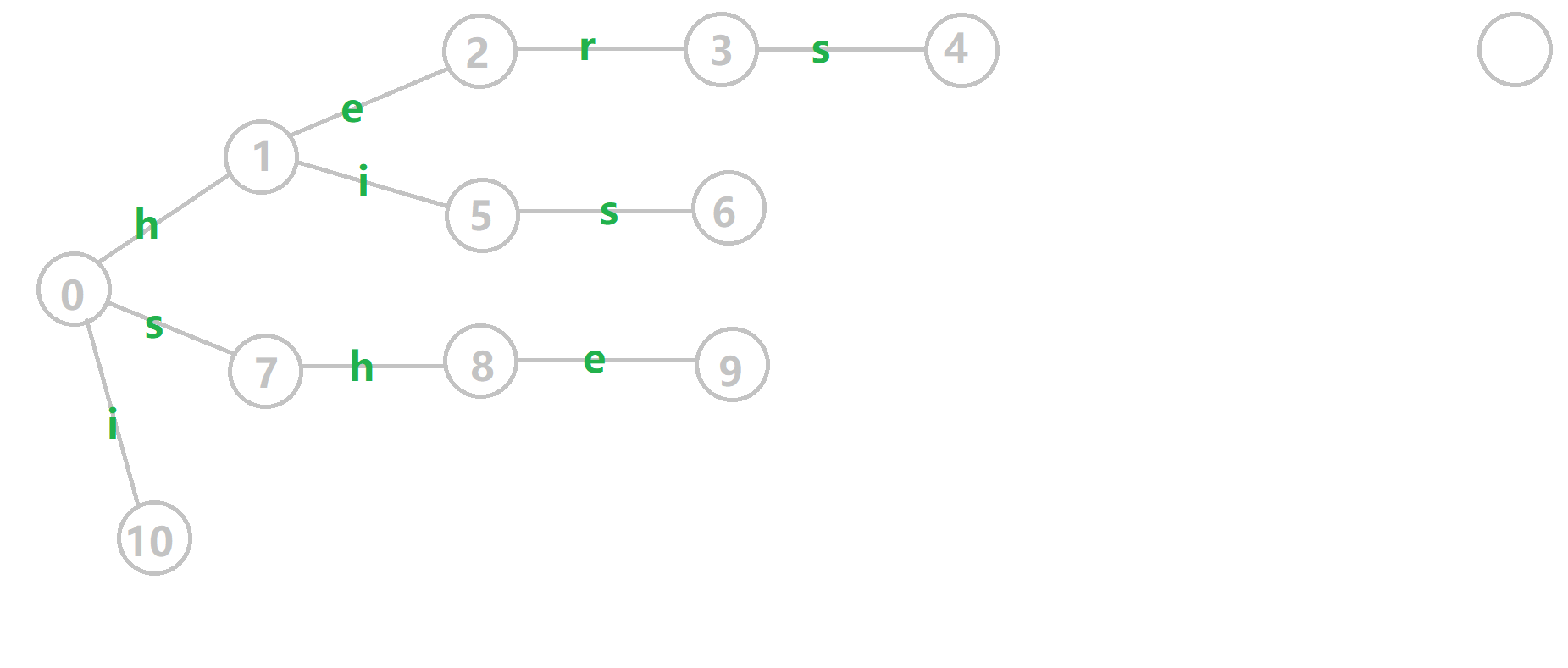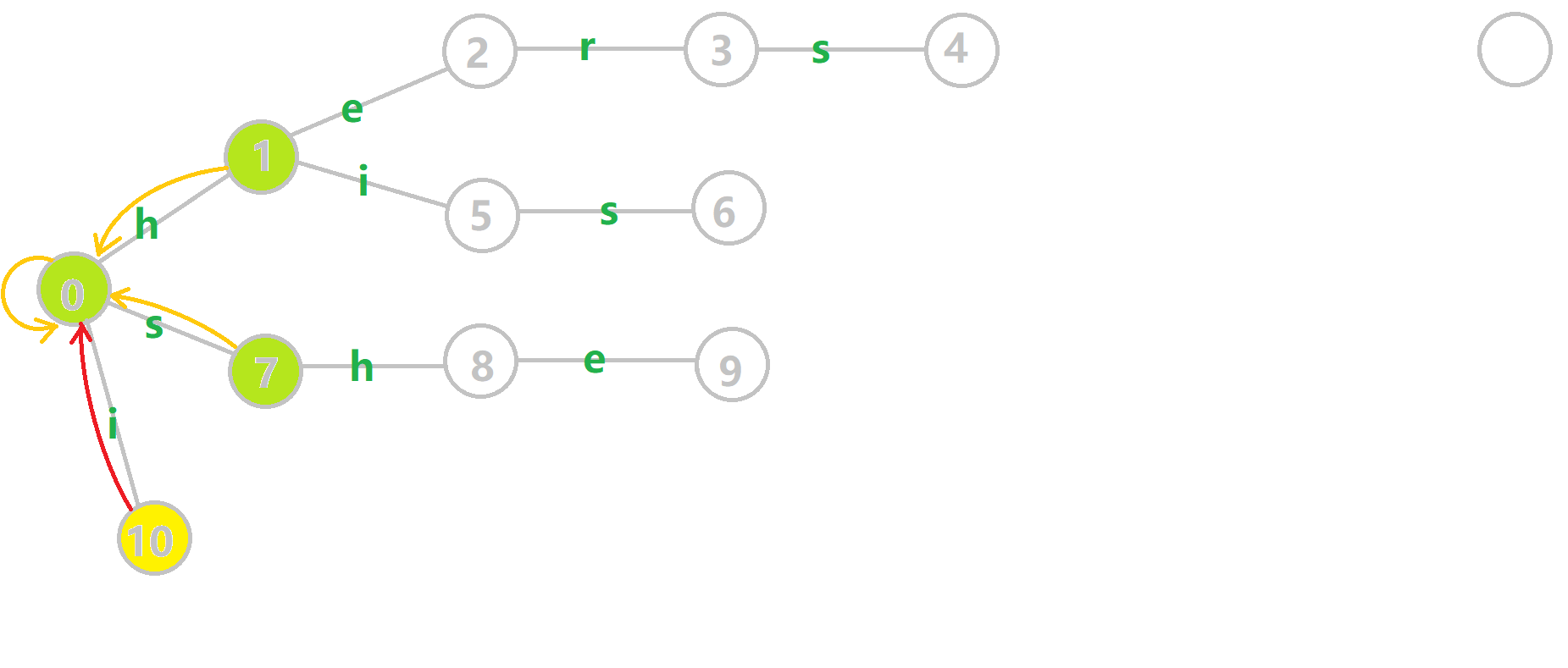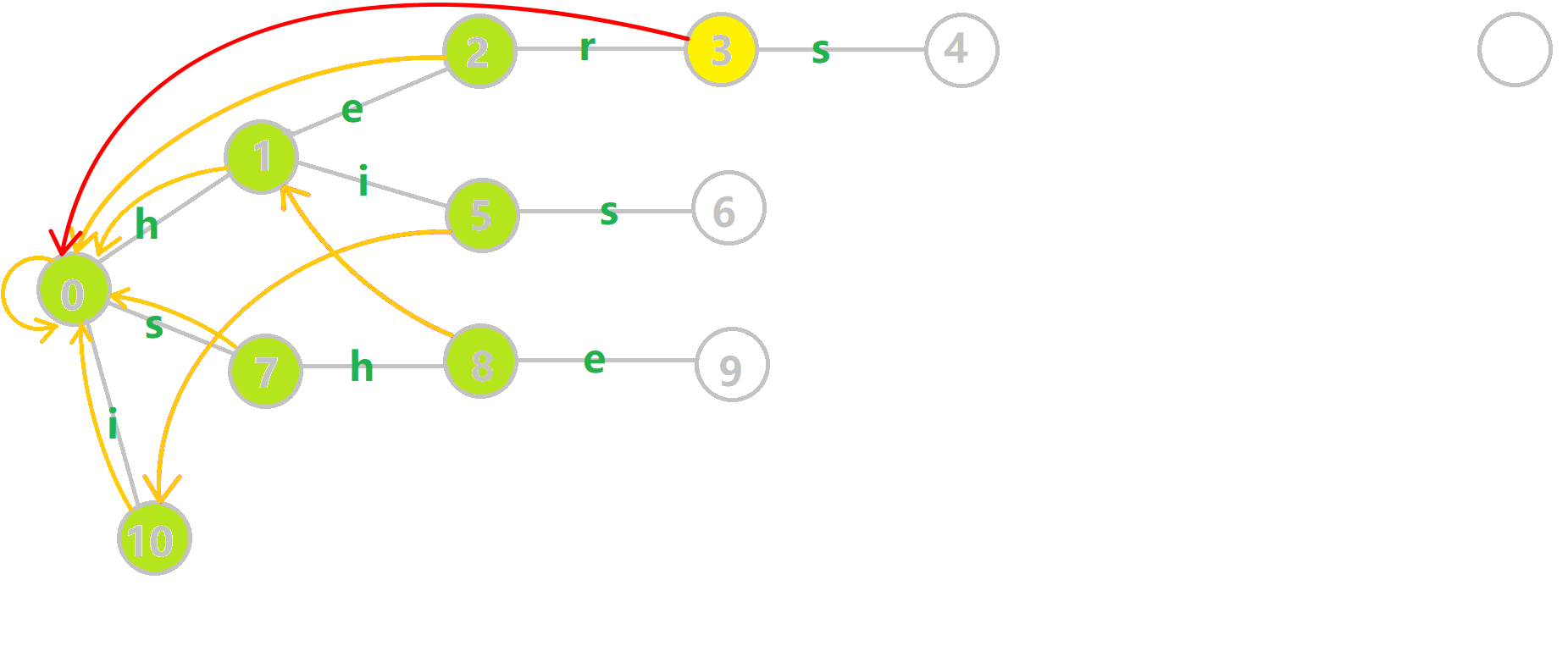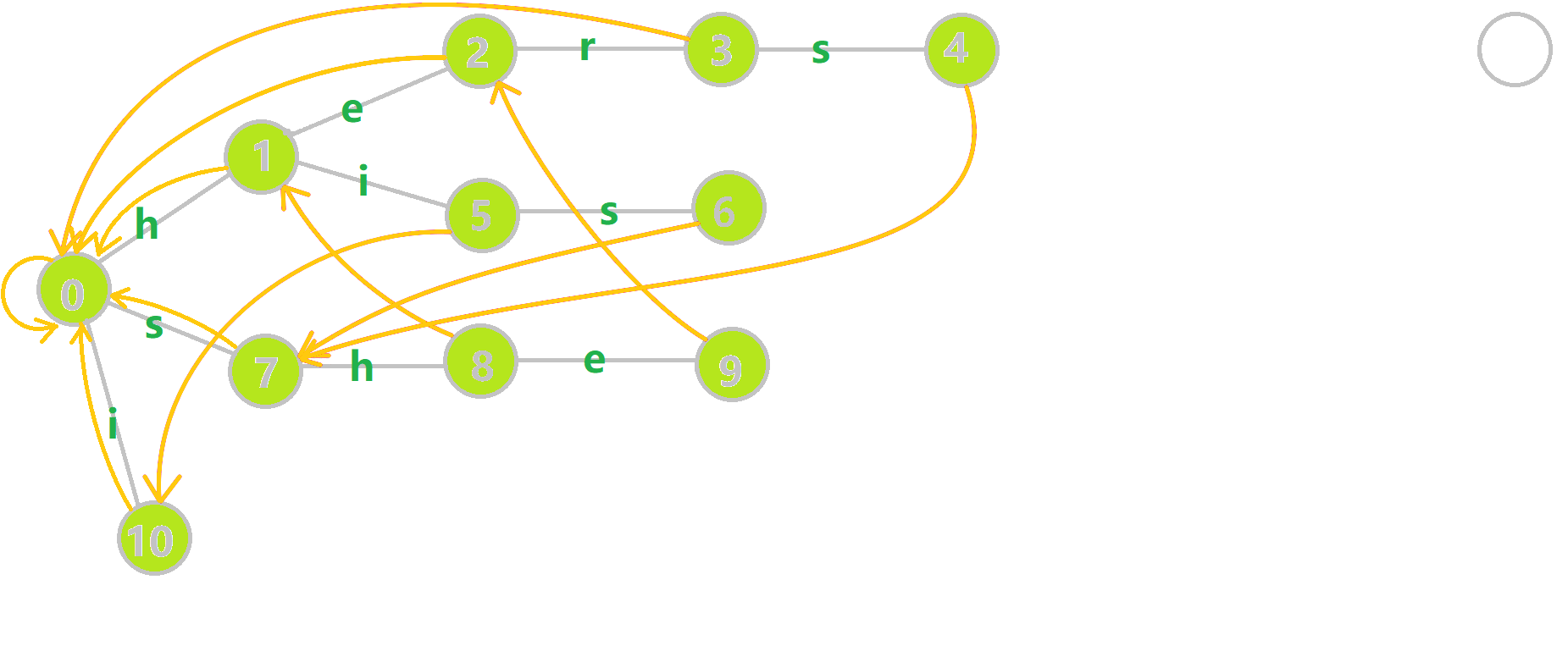
其中橙色和红色的边代表失配指针。
至于我们为什么要在 \(bfs\) 的时候处理 \(fail\) 指针,那就显然了,那么可以轻易得出结论:
**任意一个结点指向的 fail 指针的深度至少为它的深度 -1 **。
Trie 图的构建
Trie 图(字典图),是在对原有的 Trie 结构的基础上进行更改形成的 AC 自动机最后的图。
又好写又快
用来解决两个事情:fail 指针的处理 和 **AC 自动机的构建 **。
同样还是 bfs 更新子结点,在这里我们不妨把 \(t[p][c]\) 看成从 \(S\) 后加一个字符 \(c\) 形成的 新状态 。(即一个状态转移函数 \(trans(u,c)\))
类似于上面构造 \(fail\) 指针的过程,还是分两种情况讨论:
-
\(t[p][c]\) 存在,则让 \(t[p][c]\) 的 \(fail\) 指针指向 \(t[fail[p]][c]\) 。
-
否则如果不存在这个转移函数,我们就让这个转移函数 \(t[p][c]\) 指向 \(t[fail[p]][c]\) 。
这似乎有一个问题:我们之前在构建 \(fail\) 指针的时候得满足合法才能停止跳 \(fail\) 更新子节点的 \(fail\) 指针。
可以说我们通过灵魂操作 2 保证了 比当前结点 \(t[p][c]\) 深度低的点的儿子都填满了。
操作二的意义就是:我们之前可能会失配后跳 \(fail\) 指针多次才能来到下一个能够匹配到的位置,但是通过操作二,可以让失配的位置直接指向它下一个要匹配的位置。
这样修改字典树的结构,使得 匹配转移更加完善 。同时它将 fail 指针跳转的路径做了压缩(就像并查集的路径压缩),使得本来需要跳很多次 fail 指针变成跳一次。
这也是 Trie 图常数小的原因。
再来看一张动图:
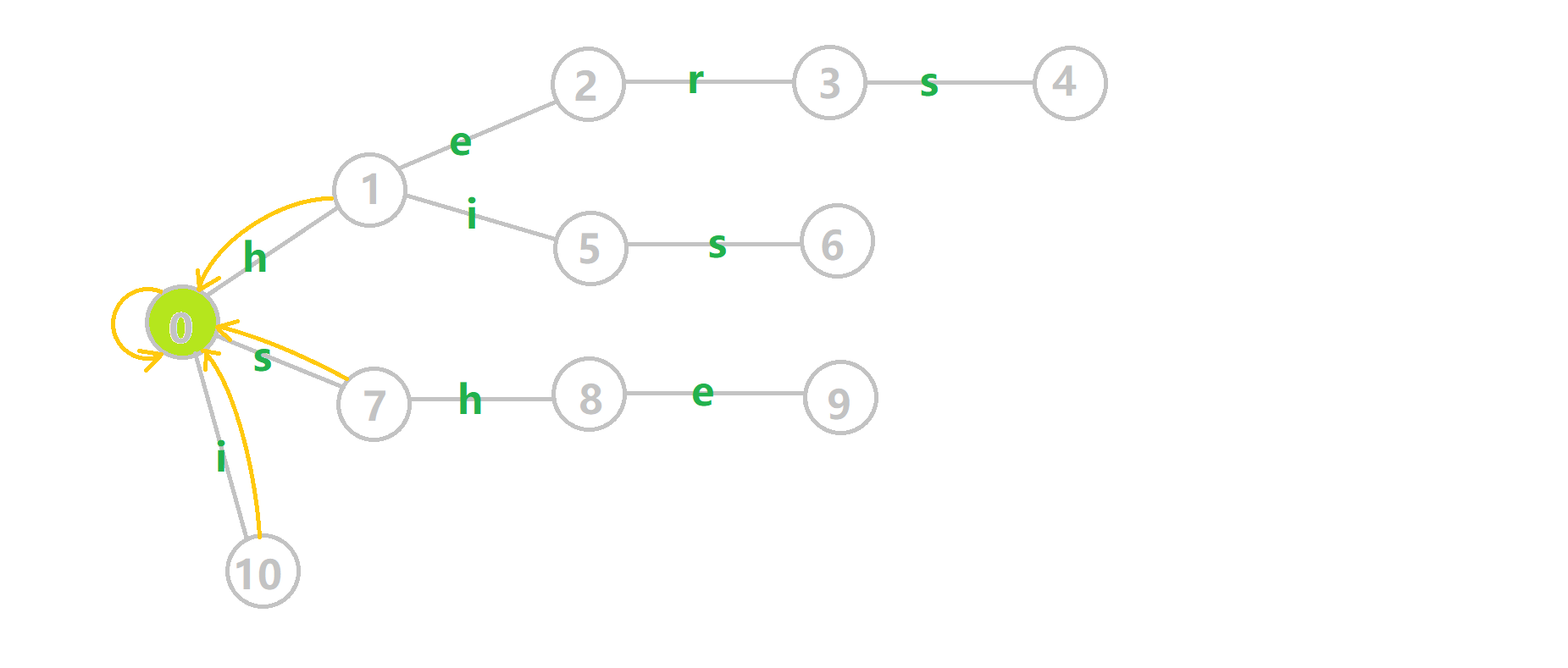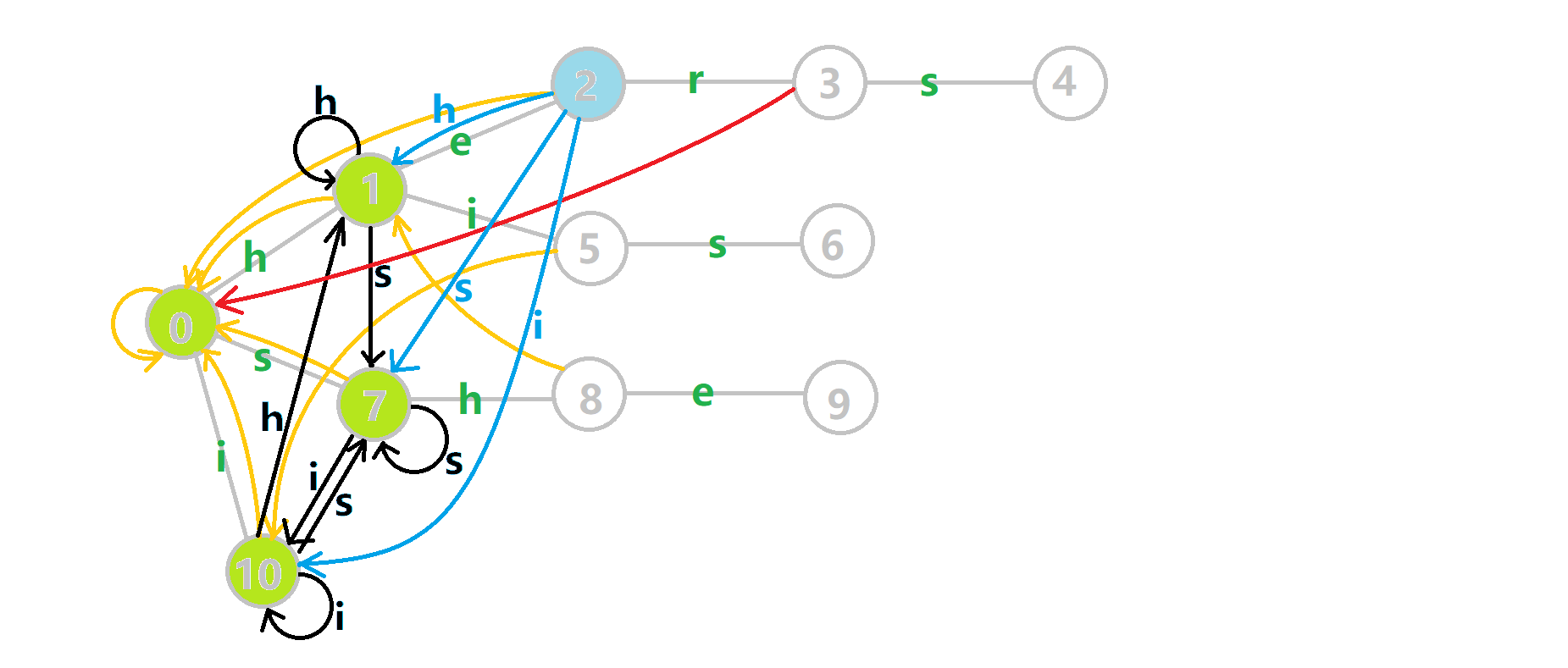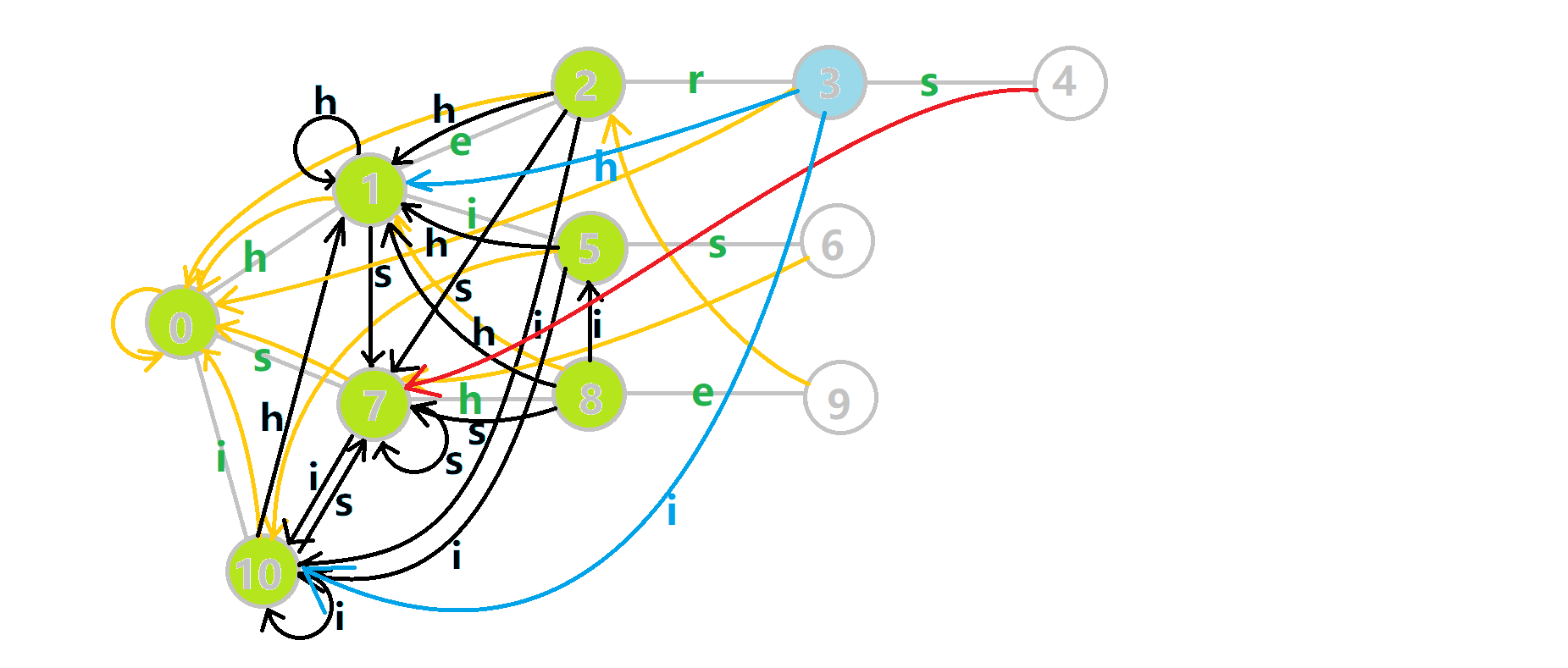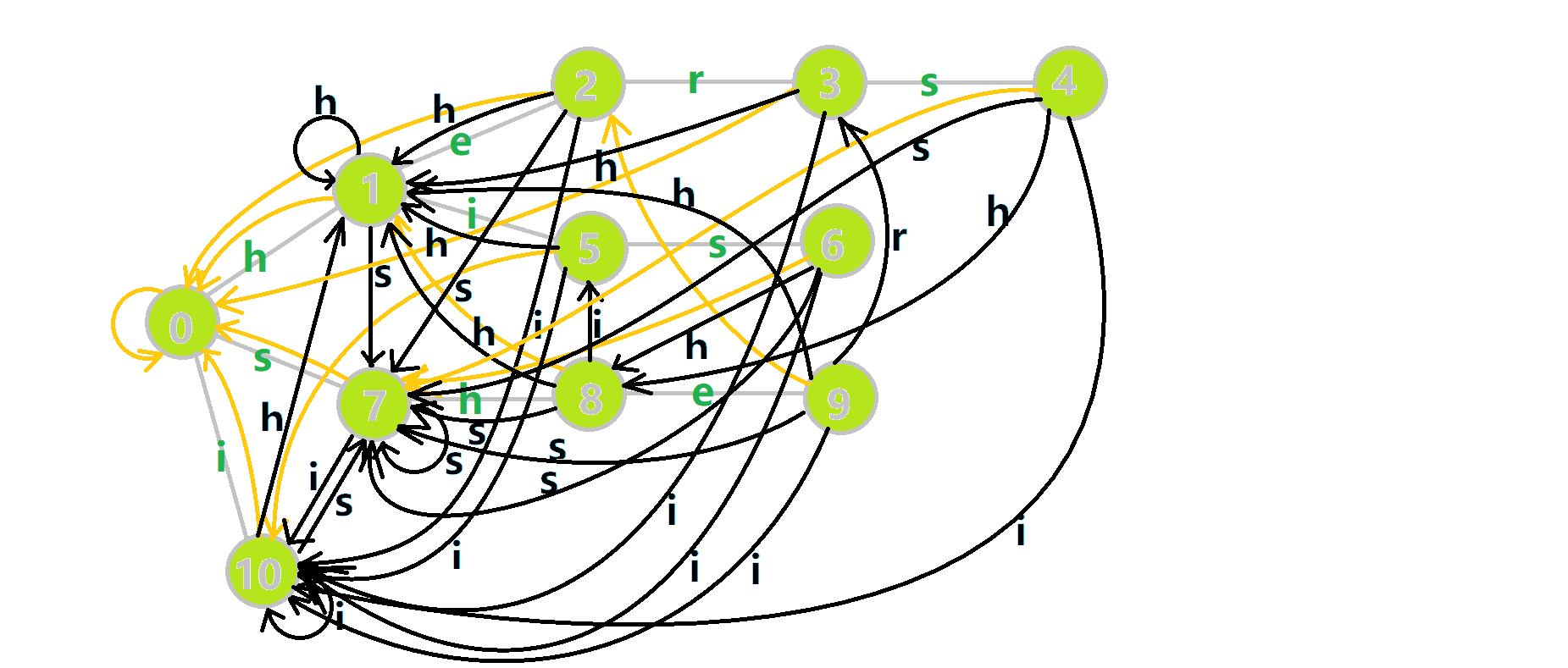
黑色的边代表在 Trie 树上修改转移函数得到的边,黄色的边代表 \(fail\) 指针。
如何理解这个东西?比如我们看四号结点的 \(trans(4,h)\) 更新情况。

先找到 \(fail[4]=7\) ,然后发现有 \(trans(7,h)\) 转移函数指向 \(8\) 号结点,那么 \(trans(4,h)\) 就是 \(8\) 号结点。
这个明显是有意义的,比如当前文本串 \(T\) 匹配了 \(h-e-r-s\) ,接下来一个字符恰好是 \(h\) ,我们通过它的 \(trans(4,h)\) 转移函数保证了一个尽量长的后缀。
小 \(tip\):不难发现自环只能发生在 \(bfs\) 的第一层。
void build(){
for(int i=0;i<26;i++){
if(t[0][i])q.push(t[0][i]);
}
while(q.size()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[u][i])fail[t[u][i]]=t[fail[u]][i],q.push(t[u][i]);
else t[u][i]=t[fail[u]][i];
}
}
}
多模式匹配操作
查询操作在建完 Trie 图后就简单了,分为两步:
-
在 Trie 图(树)上进行自我和树的匹配。(因为儿子都被填满了)
-
在匹配到的当前结点跳失配指针,并进行答案求解后清空标记数组。
int query(char *s){
int u=0,res=0;
for(int i=1;s[i];i++){
u=t[u][s[i]-'a'];
for(int j=u;j && end[j]!=-1;j=fail[j]){
res+=end[j];end[j]=-1;
}
}
return res;
}
由于跳 \(fail\) 指针是唯一的,所以一个点 \(end[j]=-1\) 当且仅当 \(j\) 在 \(fail\) 指针的路径上到根已经被打通了,这样做可以保证复杂度。
还是来一张多模式匹配动图:
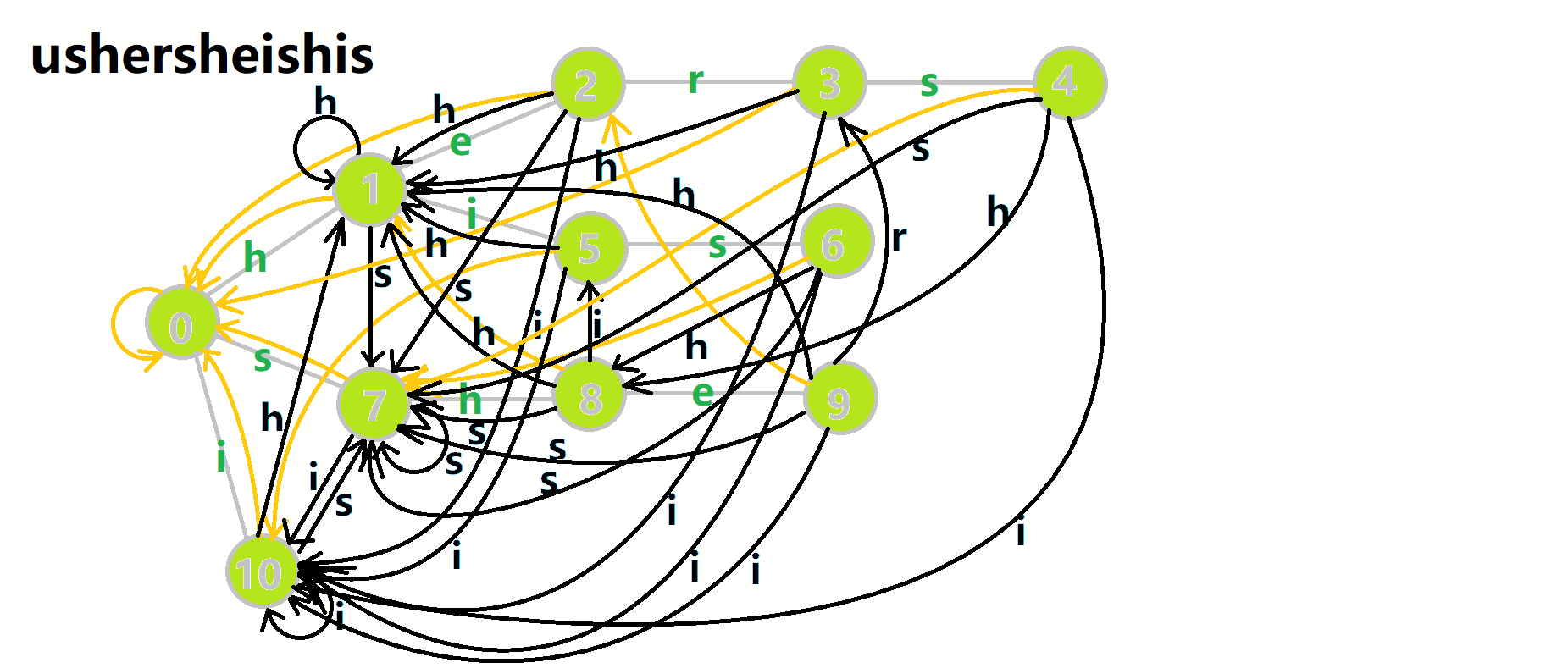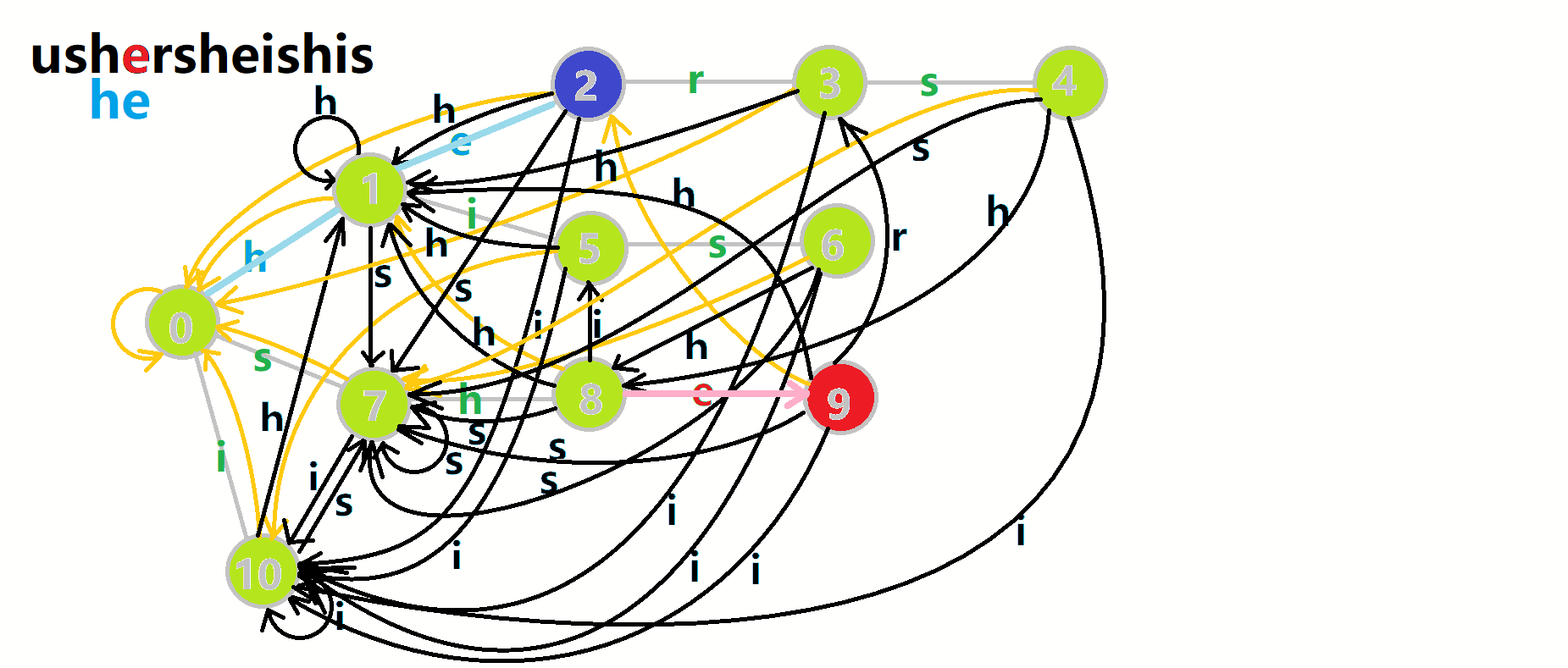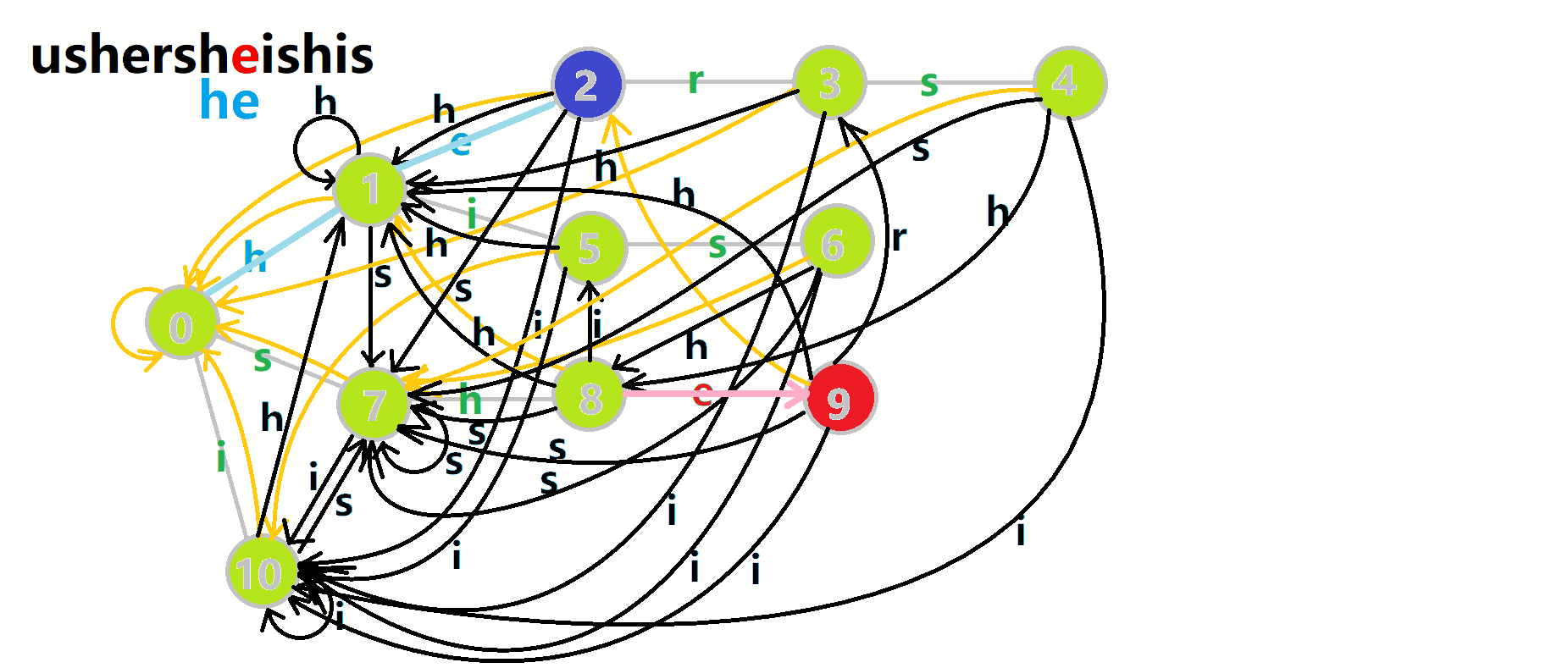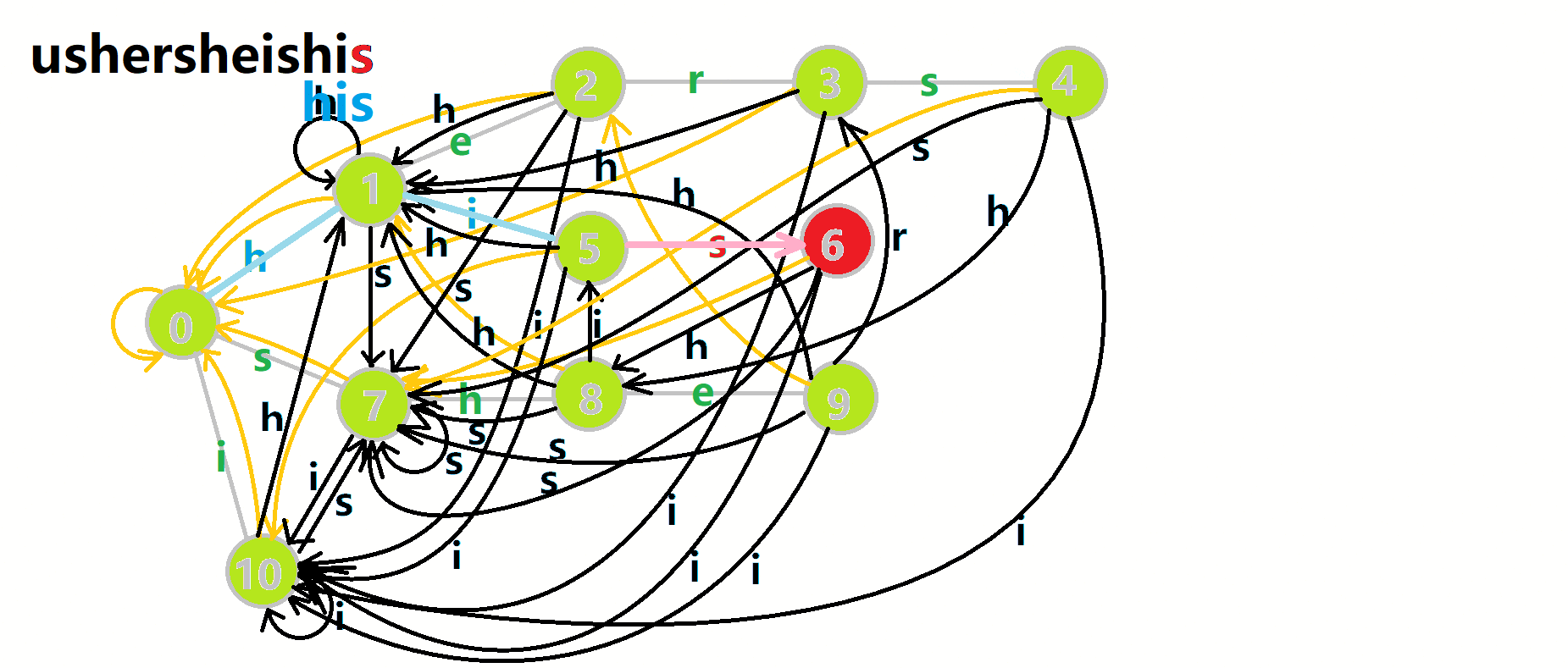
可以发现,在匹配完 \(s-h-e\) 后失配 \(r\) 的时候,直接跳到了 \(3\) 的位置,这也是最佳位置。
板子们
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
T x=0;char ch=getchar();bool fl=false;
while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
}
return fl?-x:x;
}
#define read() read<int>()
const int maxn = 1e6 + 6;
int n;
#include <queue>
namespace AC{
int t[maxn][26],cnt,end[maxn],fail[maxn];
void insert(char *s){
int u=0;
for(int i=1;s[i];i++){
if(!t[u][s[i]-'a'])t[u][s[i]-'a']=++cnt;
u=t[u][s[i]-'a'];
}
end[u]++;
}
queue<int> q;
void build(){
for(int i=0;i<26;i++){
if(t[0][i])q.push(t[0][i]);
}
while(q.size()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[u][i])fail[t[u][i]]=t[fail[u]][i],q.push(t[u][i]);
else t[u][i]=t[fail[u]][i];
}
}
}
int query(char *s){
int u=0,res=0;
for(int i=1;s[i];i++){
u=t[u][s[i]-'a'];
for(int j=u;j && end[j]!=-1;j=fail[j]){
res+=end[j];end[j]=-1;
}
}
return res;
}
}
using namespace AC;
char s[maxn];
#define read() read<int>()
int main(){
n=read();
for(int i=1;i<=n;i++)scanf("%s",s+1),insert(s);
scanf("%s",s+1);
build();
printf("%d\n",query(s));
return 0;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
T x=0;char ch=getchar();bool fl=false;
while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
}
return fl?-x:x;
}
#define read() read<int>()
const int maxn = 1e6 + 6;
int n;
#include <queue>
namespace AC{
int t[maxn][26],cnt,fail[maxn],val[maxn],idx[maxn],tot[200];
void insert(char *s,int id){
int u=0;
for(int i=1;s[i];i++){
if(!t[u][s[i]-'a'])t[u][s[i]-'a']=++cnt;
u=t[u][s[i]-'a'];
}
idx[u]=id;
}
queue<int> q;
void build(){
for(int i=0;i<26;i++){
if(t[0][i])q.push(t[0][i]);
}
while(q.size()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[u][i])fail[t[u][i]]=t[fail[u]][i],q.push(t[u][i]);
else t[u][i]=t[fail[u]][i];
}
}
}
inline void init(){
cnt=0;
memset(fail,0,sizeof fail);
memset(t,0,sizeof t);
memset(val,0,sizeof val);
memset(idx,0,sizeof idx);
memset(tot,0,sizeof tot);
}
int query(char *s){
int u=0,res=0;
for(int i=1;s[i];i++){
u=t[u][s[i]-'a'];
for(int j=u;j;j=fail[j]){
val[j]++;
}
}
for(int i=0;i<=cnt;i++)if(idx[i])res=max(res,val[i]),tot[idx[i]]=val[i];
return res;
}
}
using namespace AC;
char s[200][107],T[maxn];
#define read() read<int>()
int main(){
while(scanf("%d",&n)==1){
if(!n)break;
init();
for(int i=1;i<=n;i++)cin>>s[i]+1,insert(s[i],i);
build();
cin>>T+1;
int x=query(T);
printf("%d\n",x);
for(int i=1;i<=n;i++)if(tot[i]==x)printf("%s\n",s[i]+1);
}
return 0;
}
加强版唯一的区别就是需要记录最多位置,因此不能用上一题的套路清空\(end\) 数组了。(其实没有 \(end\) 数组)
- 感谢 OI-wiki 的信息 。


