[题解] P4363 [九省联考2018]一双木棋chess

[题解] P4363 [九省联考2018]一双木棋chess

传送门

轮廓线状态压缩 \(DP\)

题意

博弈游戏，两人轮换填数。

一个格子可以被填上数 当且仅当 其上面和左面的格子都填上了数。

两人都希望自己的分数之和减去对面的分数之和最小，求出最小值（单向，即 \(min\{sum1-sum2\}\)）。

题解

观察题目不难发现，题中的合法形态为 无数个上三角状（锯齿状）。

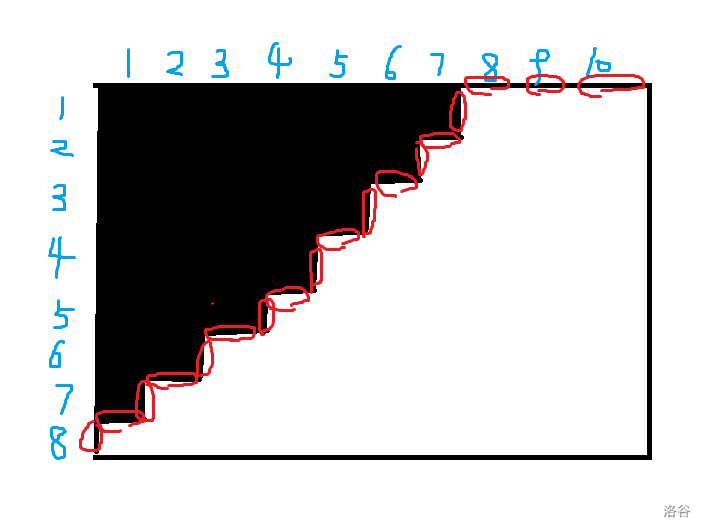
\(P.S.\)图片来自 @ LawrenceSivan。

\(n,m\) 不大，考虑状压轮廓线，竖直线为 \(1\) ，水平线为 \(0\)，例如上图状态为：

\(101010101010101000\)

可以惊奇的发现，这个状态是有利于转移的（但也不利于转移）。

有利于转移是因为不用引进别的状态，不利于转移是因为没有确定的转移顺序。

由于转移顺序难以确定，记忆化搜索即可。

记忆化搜索

• 用于 目标状态唯一确定 或者 搜索顺序部分已知（滑雪） 的 \(DP\) 实现方式，其意义为 该状态到目标状态的答案。

• 免除了大量的 冗杂状态，保留的仅仅为合法状态（例如在有些递推中需要将不合法值设成 \(-1\) ）。

• 玄学，可以骗分。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
	T x=0;char ch=getchar();bool fl=false;
	while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
	}
	return fl?-x:x;
}
const int maxn = 21;
int a[maxn][maxn],b[maxn][maxn];
int n,m,f[1<<maxn],s,t;
bool vis[1<<maxn];
const int INF = 0x3f3f3f3f;
#define read() read<int>()
int dfs(int s,int type){
	if(vis[s])return f[s];
	vis[s]=true;
	f[s]=type?-INF:INF;//1/2
	int x=n+1,y=1;
	for(int i=n+m-1;i>0;i--){//高位开始
		if((s>>i)&1)x--;
		else y++;
		if(!((s>>i)&1) || ((s>>i-1)&1))continue;//找到 10 拐角并进行转移
		if(type)f[s]=max(f[s],a[x][y]+dfs(s^(3<<i-1),0));//把 10 变成 01
		else f[s]=min(f[s],dfs(s^(3<<i-1),1)-b[x][y]);
	}
	return f[s];
}
int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)a[i][j]=read();
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)b[i][j]=read();
	int s=((1<<n)-1)<<m,t=(1<<n)-1;//起始状态与目标状态
	vis[t]=true;f[t]=0;
	dfs(s,1);
	printf("%d\n",f[s]);
	return 0;
}