[总结] 基环树
[总结] 基环树
基环树 \(\in\) \(NOIP\) 考纲
概念类
基环树的def
-
与普通树类似,仅仅看上去形态多了一个环(可以理解为树加了一条边),所以叫基环树。
-
基环树的顶点数和边数相等。
类似这样:( \(copy\) 的 )
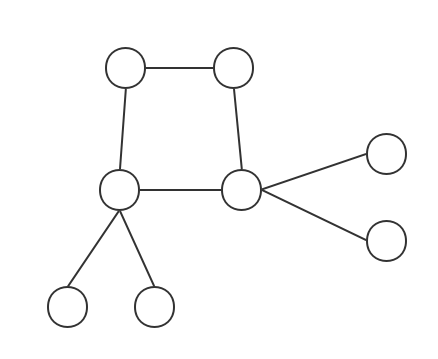
还有这样:(外向树)
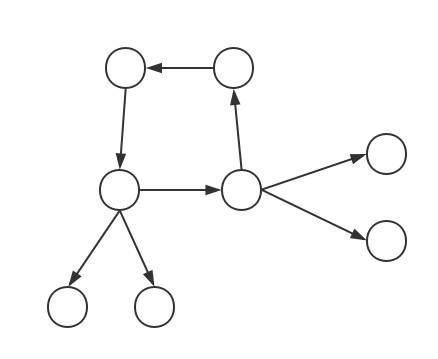 、
、
当然还有这样:(内向树)
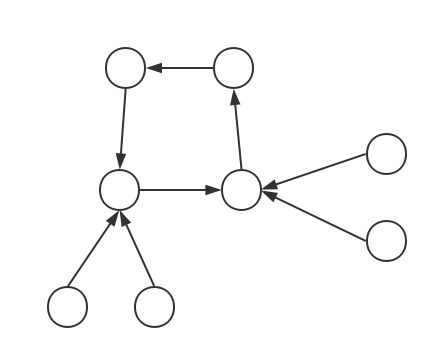
基环树直径def
- 和普通树直径类似,基环树只是要处理跨越环的那一部分

如这张图,直径为:
\(5->1->3->6\)
环为:
\(1->4->3\)
基环树性质
求(基环)树的最小 \(dfs\) 序。
如果是树:
\(vector\) 直接排序 \(dfs\) 即可。
如果是基环树:
- 枚举删边,\(dfs\) 求最小即可。
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn=5050;
vector <int> G[maxn];
int edge[maxn][2],ans[maxn];
int n,m;
namespace solve1{
bool vis[maxn];
int cnt = 0;
void dfs(int u,int fa){
ans[++cnt]=u;
vis[u]=true;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(!vis[v])dfs(v,u);
}
}
void main(){
for(int i=1;i<=n;i++){
sort(G[i].begin(),G[i].end());
}
memset(vis,false,sizeof vis);
dfs(1,0);
for(int i=1;i<=cnt;i++)printf("%d ",ans[i]);
}
}
namespace solve2{
bool vis[maxn];
int cnt=0,res[maxn],delu,delv;
bool cmp(){
for(int i=1;i<=n;i++)if(ans[i]!=res[i])return ans[i]>res[i];
return false;
}
bool check(int u,int v){
if((delu==u&&delv==v) || (delu==v&&delv==u))return false;
return true;
}
void dfs(int u,int fa){
res[++cnt]=u;
vis[u]=true;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(!vis[v]&&check(u,v))dfs(v,u);
}
}
void main(){
memset(ans,0x3f,sizeof ans);
for(int i=1;i<=n;i++)sort(G[i].begin(),G[i].end());
for(int i=1;i<=m;i++){
cnt=0;
delu=edge[i][0],delv=edge[i][1];
memset(vis,0,sizeof vis);
memset(res,0,sizeof res);
dfs(1,0);
if(cmp()&&cnt==n)memcpy(ans,res,sizeof res);
}
for(int i=1;i<=n;i++)printf("%d ",ans[i]);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
G[u].push_back(v);G[v].push_back(u);
edge[i][0]=u;edge[i][1]=v;
}
if(m==n)solve2::main();
else solve1::main();
return 0;
}
基环树求直径
基环树找环
暂时发现三种方法:
- \(dfs\) 找环
void dfs(int u){
vis[u]=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(vis[v]==1)continue;
if(vis[v]==-1)tot++;//环的个数
else if(vis[v]==0)dfs(v);
}
vis[u]=1;
}
- \(topo\) 找环
void topsort(){
queue<int> q;
for(int i=1;i<=n;i++)if(!ru[i])q.push(i);
while(q.size()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(--ru[v]==0)q.push(v);
}
}
}
最后 \(in[u]\geq 1\) 的点就是环内的点(其实有入度的点就在环内)
缺点是磨灭了原始图结构
- 首选:栈
他的优点就是保留了原始的图结构
细节还是比较多的,记得在回溯完的时候弹栈
void tarjan(int u,int fa){
stk[++top]=u;vis[u]=true;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
if(!vis[v])tarjan(v,u);
else if(!fl){//标志bool有必要
fl=true;
int tmp;
do{
tmp=stk[top--];on[top]=true;
cir[++len]=u;
}while(tmp!=v);
}
}
if(stk[top]==u)--top;
}
求直径
求直径的过程本质上就是在基环树上DP的过程
找到环之后,像普通树一样找到以环上每个结点为根的子树的直径
void dfs(int u,int fa){
f[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa || on[v])continue;//在环上的情况是要考虑的
dfs(v,u);
zhi=max(zhi,f[u]+f[v]+e[i].w);//用未更新的f[u]更新直径
f[u]=max(f[u],f[v]+e[i].w);//更新f[u]
}
}
然后考虑环上的情况。
考虑环的后效性处理,断环为链,复制一倍。
不难列出方程:
\(ans=max(ans,f[i]+f[j]+sum[i]-sum[j])\)
其中:\(i-j+1\leq len\),即 \(i-j<len\)
发现可以单调队列优化(决策集合的滑动窗口)。
for(int i=1;i<=(len<<1);i++){
while(hd<=tail && i-q[hd]>=len)hd++;
if(i!=1)res=max(res,f[cir[i]]+f[cir[q[hd]]]+sum[i]-sum[q[hd]]);
while(hd<=tail && f[cir[q[tail]]]-sum[q[tail]]<f[cir[i]]-sum[i])tail--;
q[++tail]=i;
}
求基环树直径的和。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
T x=0;char ch=getchar();bool fl=false;
while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
}
return fl?-x:x;
}
const int maxn = 1e6 + 10;
#define LL long long
struct edge{
int to,nxt;LL w;
}e[maxn<<1];
int head[maxn],cnt=1;
inline void link(int u,int v,LL w){
e[++cnt].to=v;e[cnt].nxt=head[u];head[u]=cnt;e[cnt].w=w;
}
int n;
int stk[maxn],top=0,cir[maxn<<1],len=0;
bool vis[maxn],on[maxn];
bool fl;
void tarjan(int u,int fa){
stk[++top]=u;vis[u]=true;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(i==(fa^1))continue;
if(!vis[v]){
tarjan(v,i);
}
else if(!fl){
fl=true;
int tmp;
do{
tmp=stk[top--];cir[++len]=tmp;
on[tmp]=true;
}while(tmp!=v);
}
}
if(stk[top]==u)top--;
}
LL f[maxn],zhi,sum[maxn<<1];
void dfs(int u,int fa){
f[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
if(on[v])continue;
dfs(v,u);
zhi=max(zhi,f[u]+e[i].w+f[v]);
f[u]=max(f[u],f[v]+e[i].w);
}
}
inline void init(){
fl=false;top=0;
len=0;
}
int to[maxn],q[maxn<<1],hd,tail;
LL v[maxn];
LL solve(int rt){
LL res=0;
init();tarjan(rt,0);
for(int i=1;i<=len;i++){
zhi=0;dfs(cir[i],0);
res=max(res,zhi);
cir[i+len]=cir[i];
}
sum[1]=0;
for(int i=2;i<=(len<<1);i++){
sum[i]=(to[cir[i-1]]==cir[i])?v[cir[i-1]]:v[cir[i]];
sum[i]+=sum[i-1];
}
hd=1;tail=0;
for(int i=1;i<=(len<<1);i++){
while(hd<=tail && i-q[hd]>=len)hd++;
if(i!=1)res=max(res,f[cir[i]]+f[cir[q[hd]]]+sum[i]-sum[q[hd]]);
while(hd<=tail && f[cir[q[tail]]]-sum[q[tail]]<f[cir[i]]-sum[i])tail--;
q[++tail]=i;
}
return res;
}
LL ans=0;
int main(){
n=read<int>();
for(int i=1;i<=n;i++){
int V=read<int>();LL w=read<LL>();
link(i,V,w);link(V,i,w);
to[i]=V;v[i]=w;
}
for(int i=1;i<=n;i++){
if(!vis[i])ans+=solve(i);//cerr<<"@"<<endl;
}
printf("%lld\n",ans);
return 0;
}


