[动态规划] 斜率优化
[动态规划] 斜率优化
$\ $
与单调队列优化的区别
前面讲过,单调队列优化的是状态变量和决策变量分开的动态规划(在转移式中可以进行分离)
比如一些类似于:
\(ans=max\{S[i]-min_{i-M\leq j\leq i-1}\{S[j]\} \}\)
\(F[i,j]=max_{j-L_i\leq k\leq S_i-1}\{F[i-1,k]+P_i*(j-k)\}\)
这都是状态和决策可以分离的,对于每一个阶段维护一个单调队列,还有下面的多重背包:
\(F[u+p*V_i]=max_{p-C_i\leq k\leq p-1}\{F[u+k*V_i]+(p-k)*W_i\}\)
详见:单调队列优化DP
总结一下,无妨就是 多项式 \(val(i,j)\) 的每一项仅与一个未知量有关
斜率优化的特点
-
斜率优化用于解决 \(val(i,j)\) 包含 \(i,j\) 乘积项的问题
-
结合计算几何知识得到最小值或最大值
-
最小值对应下凸包,最大值对应上凸包,因题而定
其思路来自于一个叫线性规划的东西:
把 \(z=-2x+y\) 转化成 \(y=kx+b\) 的形式
典型例题
P3195 [HNOI2008]玩具装箱
不管什么优化,先写出递推式才是最重要的
\(f[i]=min\{f[j]+(sum[i]-sum[j]+i-j-L-1)^2\}\)
其中 \(j\in(0,i)\),并没有什么限制
对式子转化成 \(y=kx+b\) 的形式
-
\(f[i]=min\{f[j]+(sum[i]+i-(sum[j]+j+L+1))^2\}\)
-
\(A[i]=sum[i]+i,B[j]=sum[j]+j+L+1\)
-
我们希望把 \(i\) 和 \(j\) 打包,让求得的 \(f[i]\) 变成截距
-
\(f[j]+B[j]^2=2*A[i]*B[j]+f[i]-A[i]^2\)(把i和j一定要分离开)
然后 \(f[i]-A[i]^2\) 变成了截距 \(b\) ,\(B[j]\) 看成 \(x\) ,\(f[j]+B[j]^2\) 看成 \(y\)
则 \(y=(2*A[i])x+b\) ,其中 \(x,y\) 都是只与 \(j\) 有关的不变量,这就在坐标系内确定了一个点。
对答案产生贡献的点一定在一个下凸包上
所以我们用单调队列通过斜率维护下凸包即可(斜率和 \(x\) 具有单调性),可以用滑动窗口解决。
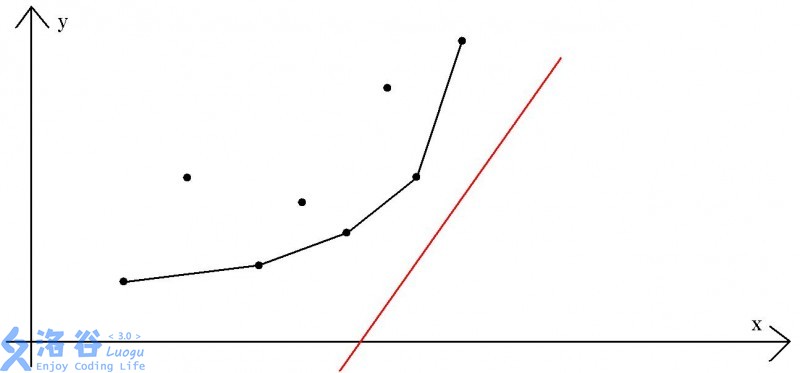
显然凸包上的斜率是单调递增的。
当循环到当前点时,及时排除不合理决策并维护下凸包,把当前点放入凸包内。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 5e4 + 10;
#define LL long long
double sum[maxn],f[maxn];
int n,L;
int head=1,tail=0,q[maxn];
inline double A(int i){return sum[i]+i;}
inline double B(int i){return A(i)+L+1;}
inline double X(int i){return B(i);}
inline double Y(int i){return f[i]+B(i)*B(i);}
inline double k(int i,int j){
return (double)(Y(j)-Y(i))/(X(j)-X(i));
}
int main(){
scanf("%d%d",&n,&L);
for(int i=1;i<=n;i++){
scanf("%lf",&sum[i]);sum[i]+=sum[i-1];
}
q[++tail]=0;//把原点放进去,否则会挂
for(int i=1;i<=n;i++){
while(head<tail && k(q[head],q[head+1])<2*A(i))head++;
f[i]=f[q[head]]+(A(i)-B(q[head]))*(A(i)-B(q[head]));
while(head<tail && k(q[tail-1],i)<k(q[tail-1],q[tail]))tail--;
q[++tail]=i;
//printf("head: %d tail: %d\n",head,tail);
}
//for(int i=1;i<=n;i++)printf("f[%d]: %.2lf\n",i,f[i]);
printf("%lld\n",(LL)f[n]);
return 0;
}
一定要把原点放在队列里
单调队列有时为了避免非空,需要把 \(head\leq tail\) 改成 \(head<tail\)
因题而定

