聊聊缓存

聊聊缓存

  • 分享人：李鹏飞

  • 分享时间：7月10日 19点30分

  • 分享主题：缓存——你之蜜糖,我之砒霜

  • 分享内容概要：有始有终，聊聊缓存在工程里的应用与在分布式下存在的问题。

  • 受众人群：想了解缓存的同学。

写在开始之前

第一次尝试系统的聊一个知识点，所以有可能有很多地方讲的不尽人意，希望大家谅解。也是基于这个原因，这一次更多是模糊的定性认识，而不是严谨的定量分析。文章的定位就是从一个点出发聊一聊，目前工业界的一个趋势和发展。

什么是缓存？& 为什么要用缓存？

缓存(Cache）是计算机领域里的一个重要概念，是优化系统性能的利器。

由于存取数据的链路漫长，计算机获取资源的成本较高。所以，非常有必要把“来之不易”的数据缓存起来，下次尽可能地复用。这样，就可以避免多次获取资源的成本，提高并发能力，也可以加快响应速度。

CPU速度：

2.5GHZ每个时钟周期为0.4ns 移位操作：大约1-2个时钟周期 ADD操作：大约占1-3个时钟周期

CPU缓存存取速度：

L1：4ns，1-5时钟周期 L2：10ns，5-20时钟周期 L3：20ns，40-100时钟周期

内存：

内存随机读取速度：100ns以内

SSD硬盘：

SSD随机访问：100μs 以内。

机械硬盘：

磁盘随机访问：15ms一次（寻道时间+旋转时间）

网络耗时

无线网络延时：20ms，加上核心网络耗时+骨干网耗时大约100ms以内。

每一层都会有两到三个数量级的差距

1秒=1000毫秒

1毫秒=1000微秒

1微秒=1000纳秒

1纳秒=1000皮秒

生活中的例子：

书桌 书架

在图书馆看书的时候，很少有人只从书架上拿一本书然后拿回书桌读，大多是都是一次性拿上好几书放到书桌上。因为随手从书桌上拿书要比去书架上成本低（去书架上拿书很有可能爬楼，去另一个书库）。

在这个例子中书桌上的书就是书架一份缓存。

缓存在计算机中的应用

操作系统OS：内存管理 页表——快表

网络IO：DNS缓存 HTTP协议 缓存

Mysql数据库内部：Chage Buffer

（插一嘴——书写是对思维的缓存）

缓存命中率？

那又怎么确定你的缓存里一定是想得到的书呢？

怎么得到有用的缓存？

这就设计到计算机领域很著名的局部性原理：程序在执行时呈现出局部性规律。

局部性原理讲的是：在一段时间内，整个程序的执行仅限于程序的某一部分，相应地，程序访问的存储空间也局限于某个内存区域。主要分为两类：

时间局部性：如果程序中的某条指令一旦执行，则不久之后该指令可能再次被执行；如果某数据被访问，则不久之后该数据可能再次被访问。（昨天借了书，那么今天也会借书的概率就会大）。

空间局部性：是指一旦程序访问了某个存储单元，则不久之后，其附近的存储单元也将被访问。（上一本借了《呐喊》，那么下一本书借《彷徨》的概率就会大）。

怎么去掉没用的缓存？

即淘汰策略。

LRU（Least Recently Used）最近最少使用（添加、查找）。

面试常问：LRU的手动实现 https://leetcode.cn/problems/lru-cache/

LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/lru-cache
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

LFU（Least Frequently Used）最不经常（记录使用次数）使用。

字节面试常问：LFU手动实现 https://leetcode.cn/problems/lfu-cache/

// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序（最左边的元素是最近的）
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1);   // cache=[1,_], cnt(1)=1
lfu.put(2, 2);   // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1);      // 返回 1
                 // cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3);   // 去除键 2 ，因为 cnt(2)=1 ，使用计数最小
                 // cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4);   // 去除键 1 ，1 和 3 的 cnt 相同，但 1 最久未使用
                 // cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4);      // 返回 4
                 // cache=[3,4], cnt(4)=2, cnt(3)=3

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/lfu-cache
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

并发场景下的数据一致性问题

image

Cache Aside Pattern（旁路缓存模式）

Cache Aside Pattern 是我们平时使用比较多的一个缓存读写模式，比较适合读请求比较多的场景。

Cache Aside Pattern 中服务端需要同时维系 DB 和 cache，并且是以 DB 的结果为准。

下面我们来看一下这个策略模式下的缓存读写步骤。

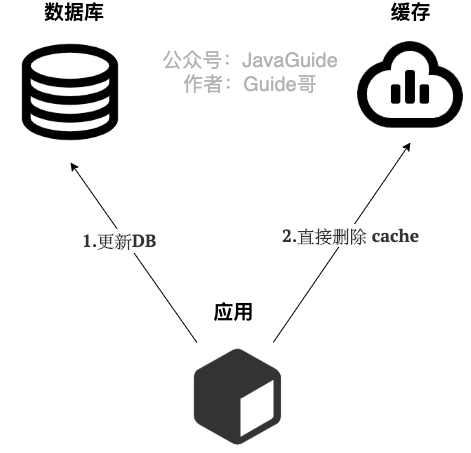
写 ：

  • 先更新 DB
  • 然后直接删除 cache 。

image

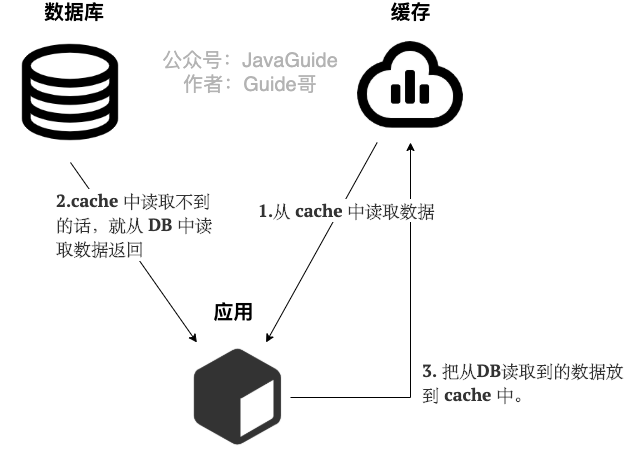
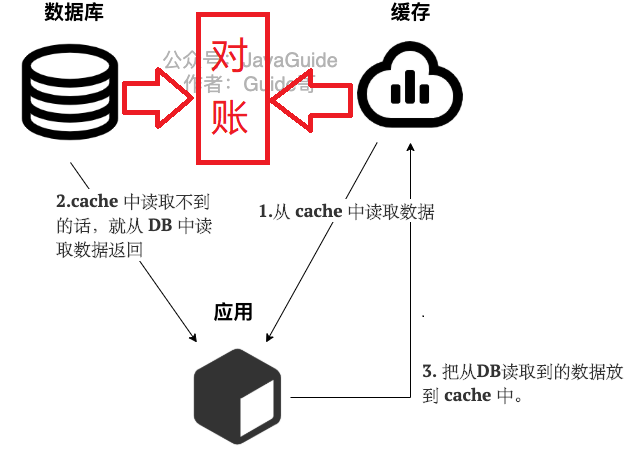
读 :

  • 从 cache 中读取数据，读取到就直接返回
  • cache中读取不到的话，就从 DB 中读取数据返回
  • 再把数据放到 cache 中。

image

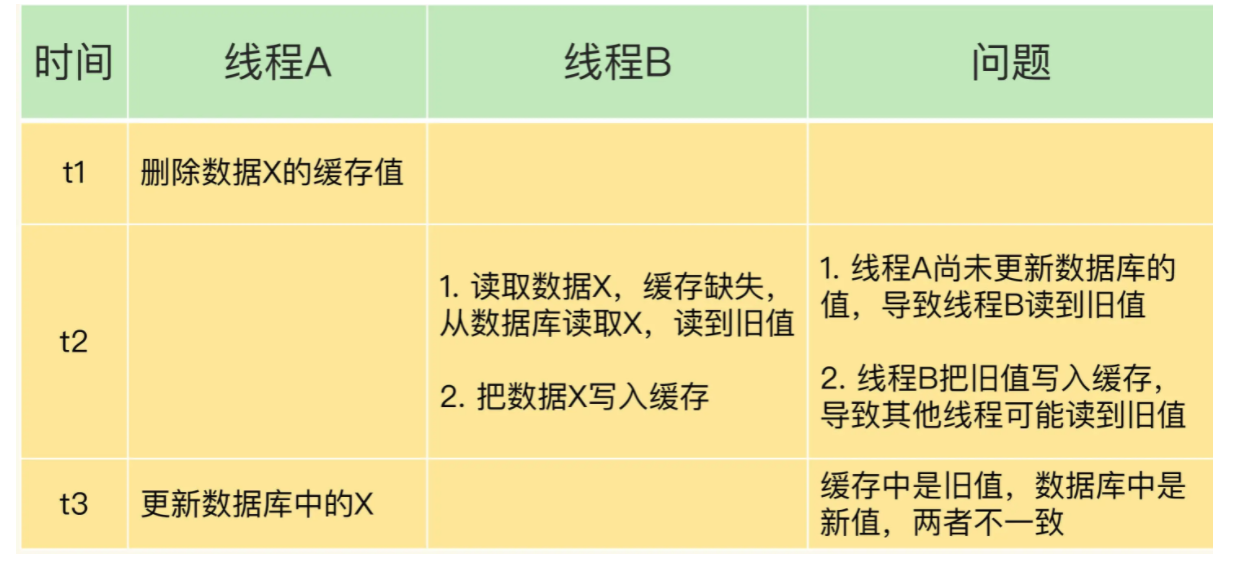
“在写数据的过程中，可以先删除 cache ，后更新 DB 么？”

答案： 那肯定是不行的！因为这样可能会造成数据库（DB）和缓存（Cache）数据不一致的问题。为什么呢？比如说请求1 先写数据A，请求2随后读数据A的话就很有可能产生数据不一致性的问题。这个过程可以简单描述为：

请求1先把cache中的A数据删除 -> 请求2从DB中读取数据->请求1再把DB中的A数据更新。

“在写数据的过程中，先更新DB，后删除cache就没有问题了么？”

答案： 理论上来说还是可能会出现数据不一致性的问题，不过概率非常小，因为缓存的写入速度是比数据库的写入速度快很多！

比如请求1先读数据 A，请求2随后写数据A，并且数据A不在缓存中的话也有可能产生数据不一致性的问题。这个过程可以简单描述为：

请求1从DB读数据A->请求2写更新数据 A 到数据库并把删除cache中的A数据->请求1将数据A写入cache。

设计缓存的过期时间

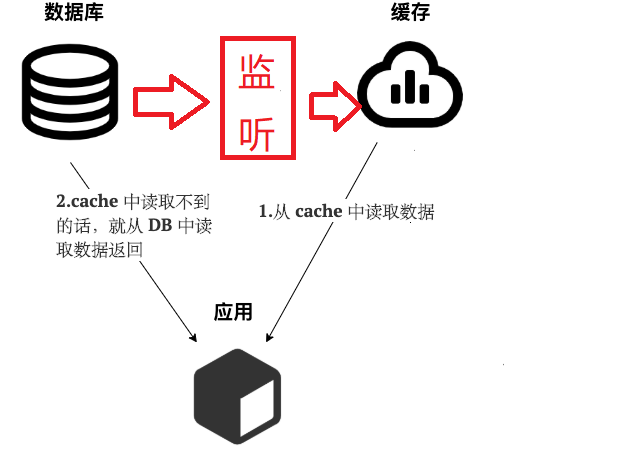
监听Canal

image

对账系统

image

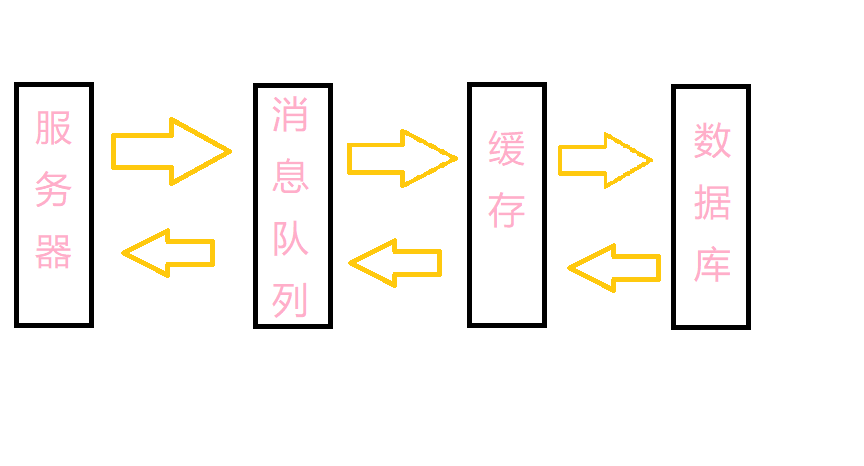
系统复杂导致的可用性下降

数据链路越长，系统可用性就会下降（一个子系统出错便会导致整个系统出错）

如果一个节点出错的概率为5%，那么有四个节点的系统出错的概率就会有（1-5%）^4就有18%，即可用性为92%，就很不能接受了。

image

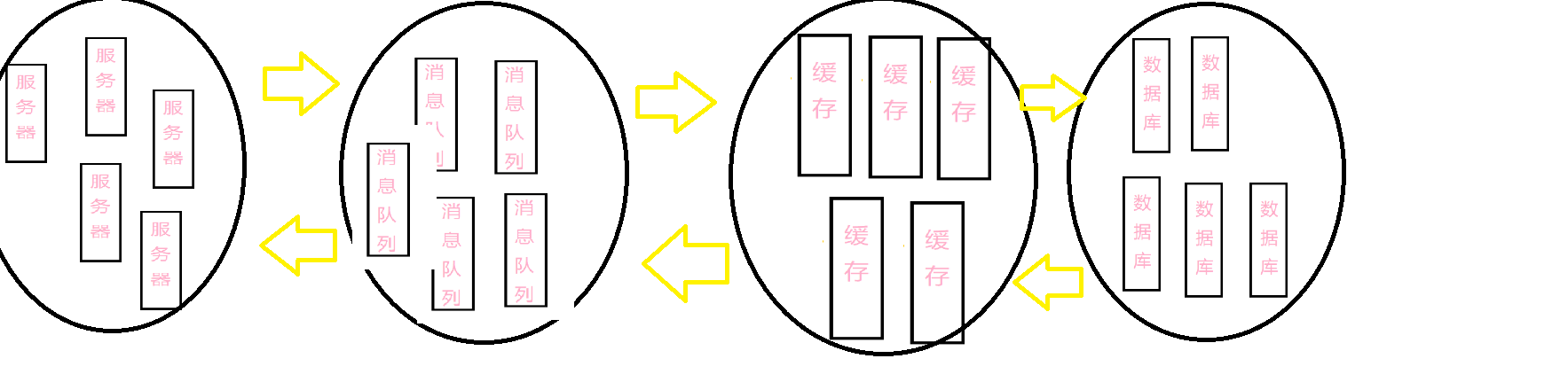
每个集群由一个Master对外提供服务，若干Slave提供备份。Master一旦出错，Slave就会选举出一个Master对外提供服务。

如果单个机器出错的概率为5%，由5台机器组成的一个节点，由于全部机器出错而导致的节点出错的概率为0.000003125%,而整个系统可用性为99.998%。

有点类似于电路里面串并联的意思。

image

不可靠的网络

网络是有时延的？

网络的不稳定的？

两将军问题

两将军问题（Two Generals' Problem）是计算机领域中的一个思想实验，是指两支由不同的将军领导的军队，正准备进攻一座坚固的城市。军队在城市附近的两个山丘扎营，中间有一个山谷将两个山丘隔开，只有两支军队同时发起进攻，才可以攻破城市。军队两个将军交流的唯一方法是派遣信使穿越山谷。然而，山谷被城市的守卫者占领，并且途经该山谷传递信息的信使有可能会被俘虏。

因此，两位将军必须通过信使沟通并约定攻击时间，并且他们都必须确保另一位将军知道自己已同意了进攻计划。但由于传递确认消息的信使可能被俘虏造成消息丢失，即使双方不断确认已收到对方的上一条信息，也无法确保对方已与自己达成共识。

达成一致进攻的共识难以实现。首先，将军A向将军B传递消息“8月4日9时整进攻”。然而，派遣信使后，将军A不知道信使是否成功穿过敌方领土。由于担心自己成为唯一的进攻军队，将军A可能会犹豫是否按计划进攻。

为了消除不确定性，将军B可以向将军A返回确认消息：“我收到了您的消息，并将在8月4日9时整进攻”。传递确认消息的信使同样可能会被敌方俘虏。由于担心将军A在没有收到确认消息的情况下退缩，将军B又会犹豫是否按计划进攻。

再次发送确认消息看上去可以解决问题—将军A再让新信使发送确认消息：“我已收到您对8月4日9时攻击计划的确认”。但是，将军A的新信使也可能被俘虏。显然，无论进行多少轮确认，都无法使两位将军确保对方已同意进攻计划。两位将军总是会怀疑他们派遣的最后一位使者是否顺利穿过敌方领土。

猜疑链——信任链

这个问题在理论上是无解的，因为你不可以通过不可靠的信道建立起可靠的通讯。

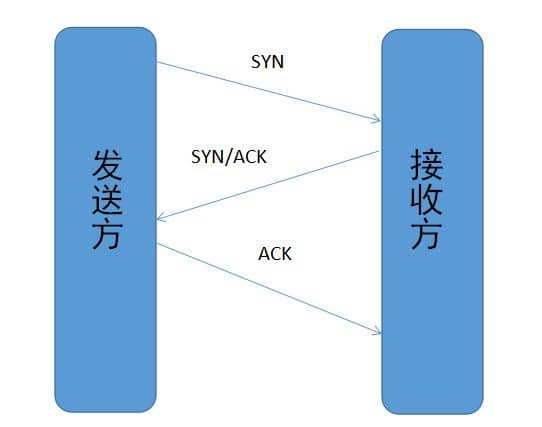
两将军问题虽然已被证明无解，仍然找到了工程上的解决方案，我们熟悉的传输控制协议（TCP）的“三次握手”就是两将军问题的一个工程解。

image

发送方与接收方都各自发送与接受了一次。

分布式场景下的数据一致性问题（了解）

共识算法

到了分布式系统里面，我们就必须考虑动态的数据如何在不可靠的网络通讯条件下，依然能在各个节点之间正确复制的问题。现在，我们来修改下要讨论的场景：如果你有一份会随时变动的数据，要确保它能正确地存储在网络中几台不同的机器上，你会怎么做？这时，你最容易想到的答案一定是“数据同步”：每当数据有变化，就把变化情况在各个节点间的复制看成是一种事务性的操作，只有系统里的每一台机器都反馈成功地完成磁盘写入后，数据的变化才能宣布成功。不过，这里有一个显而易见的缺陷，尽管可以确保 Master 和 Slave 中的数据是绝对一致的，但任何一个 Slave 节点、因为任何原因未响应都会阻塞整个事务。也就是说，每增加一个 Slave 节点，整个系统的可用性风险都会增加一分。

Paxos

Paxos 算法，是由Leslie Lamport提出的一种基于消息传递的协商共识算法。现在，Paxos 算法已经成了分布式系统最重要的理论基础，几乎就是“共识”这两字的代名词了。

2013 年，因为对分布式系统的杰出理论贡献，Lamport 获得了 2013 年的图灵奖。随后，才有了 Paxos 在区块链、分布式系统、云计算等多个领域大放异彩的故事。

Raft

Multi Paxos 对 Basic Paxos 的核心改进是，增加了“选主”的过程，利用Basic Paxos把分布式中最难的共识部分通过“选主”先解决了。 Basic Paxos是每次并发操作都需要达成共识，用共识算法跑一遍。 Multi Paxos是用共识算法先选个主节点出来，然后就开开心心地把并发操作变成了对主节点的单机操作。

posted @ 2022-07-08 21:32  飞飞很要强  阅读(181)  评论(0)  编辑  收藏  举报