2023.12.10闲话——浅谈等时圆

虽然我的物理很垃圾，但是不妨碍我写一些 whk 物理的东西！

以下是等时圆模型的一些口胡。

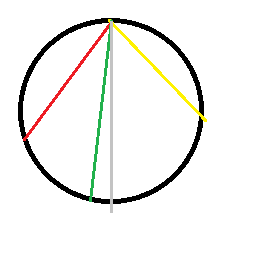
这是一个圆，从最高点下来有多个轨道，每个物体都要沿一个轨道运动，相当于每个物体从这个圆的最高点沿一个斜面运动，给定圆的半径 \(r\)，重力加速度 \(g\)，一个夹角 \(\theta\)，求各个点的到达圆上的时间。

我们先简单入手来分析一个轨道，其他的轨道大同小异，类比一下就能得到结论。

以红色的轨道来研究。

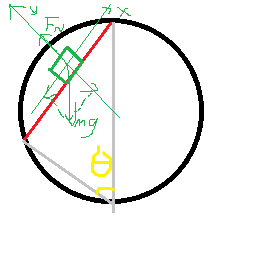
进行简单的受力分析可得，这个物体整体受一个平行于斜面向下的力，是匀加速直线运动。

设这个轨道的长度为 \(x\)，物体的加速度为 \(a\)，我们可以通过 \(x=\frac{1}{2}at^2\) 来求得其运动的时间。

可以得到 \(x=2r\sin\theta\)，\(a=\frac{mg\sin\theta}{m}=g\sin\theta\)。
即 \(2r\sin\theta=\frac{1}{2}gt^2\sin\theta\)。

我们把 \(t\) 放到左边，其他的都放到右边，可得 \(t^2=\frac{4r}{g}\)，开方之后为 \(t=\pm2\sqrt\frac{r}{g}\)，显然 \(t\) 为正数，所以 \(t=2\sqrt\frac{r}{g}\)。

然后会发现这个 \(t\) 的式子右边只有一个 \(r\) 和 \(g\)，跟哪个轨道一点关系也没有，所以这些轨道上所有物体运动的时间是相等的。

如果是不同圆的地方滑到最低点的话和这个大同小异，你会发现把圆倒放过来之后就是一个加速度为负其他都一模一样的问题。

以下是等势圆的一些应用。

平常的题目中不是每个题都是模型，很多题不是从最高点开始运动，但是我们可以给它转化一下。

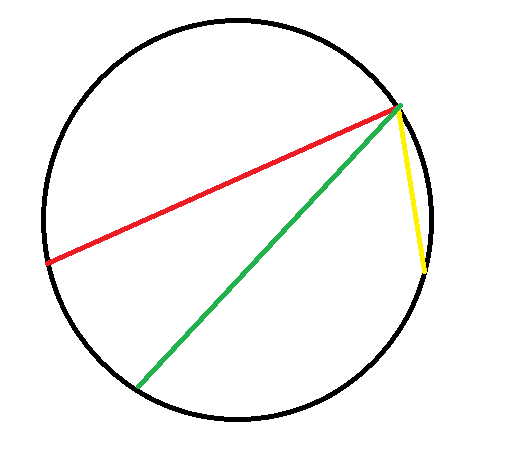
关于这个图，物体不是从最高点向下运动的，但是我们可以画几个圆使得出发的点是最高点且经过运动的终点，然后比较圆的半径/大小。

我们知道三点确定一个圆，但是我们只有两个点，不过好在还有一个信息：有一个点是圆的最高点。
也就是说，过这个点做一条竖直的直线，这条直线就是这个圆的对称轴，是过圆心的，然后再作轨道的中垂线，两个直线交点即为圆心。

还是以红的轨道为例。画出来大概是这样的。

（图画太大了/oh）

依次类推，都画出来直接比较圆的大小即可。

但是画图很费事，明明我们只需要比较半径啊。

所以我们连圆都不用画，作出圆心后连接最高点和圆心即为半径，直接比较这个更加省时省力。