字符串杂乱笔记
字符串哈希
万物皆可哈希。
将字符串压缩/映射为一个东西,一般压成一个值。
这样对这个值进行比较会更加方便、快捷。
正确性/原则:尽量让哈希出来的信息比较随机,冲突变小。
保证正确性可以既快捷又正确的处理信息。
多项式哈希
存在一个字符串 \(s\) 和一个值 \(base\),形如 \(h(s)=\sum\limits^{\left|s\right|}_{i=1}s_{i}base^{\left|s\right|-i}\) 的哈希。
由于多项式的值一般很大,所以可以对一个质数取模来方便存储。
字符的映射值
直接用 s[i]-'a' 会使得 a 的值为 \(0\),导致 a,aa,aaa 值相同。
直接用 s[i] 会使得 每个字符的值很大,导致 base 也被迫设的很大,这样调试的时候人手算会很痛苦。
所以用 s[i]-'a'+1 会好一点。
base 比较小容易调试,可以设 \(29\)。
(《可以给人看的》人言否!)
局限性
由于多项式哈希是按位独立的,会出一点问题。
例:两个串的哈希值相加容易冲突,不能代表唯一的两个串,"ab"+"cd"="ad"+"cb"。
矩阵哈希
将字符串每个字符映射为一个矩阵,将字符串中各个字符代表的矩阵乘起来即为值。
例:\(a\leftarrow \begin{bmatrix}1&1\\-1&2\end{bmatrix}\),\(b\leftarrow \begin{bmatrix}1&2\\3&4\end{bmatrix}\),abbab=\(\begin{bmatrix}1&1\\-1&2\end{bmatrix}\begin{bmatrix}1&2\\3&4\end{bmatrix}^2\begin{bmatrix}1&1\\-1&2\end{bmatrix}\begin{bmatrix}1&2\\3&4\end{bmatrix}\)。
字符映射出的矩阵直接随机一个就可以,不用手打。
矩阵哈希除了满足字符串哈希的基本性质,还可以满足一些很好的性质。
这样每个位置的值不仅与该位置的值有关,还与前后字符的一些值有关。
上面说的多项式哈希的问题就可以被解决掉。
随机两个相同的矩阵概率极其小,真发生了比买彩票中奖还顶。
可以用于计算字符串集合的哈希值。
查询
使用矩阵的逆查询是可以做到 \(O(1)\) 的。
模数为 \(P\),任取一个矩阵不可逆的概率为 \(\frac{1}{P}\)。
假设一个字符串的长度为 \(N\),则这个字符串矩阵哈希的不可逆的概率为 \((1-\frac{1}{P})^n\),使用伯努伊不等式可得这个式子约等于 \(\frac{P-N}{P}\),如果 \(N\) 远小于 \(P\) 可以近似认为式子为 \(1\)。
所以一般认为矩阵是都可逆的。
设每个字符对应的矩阵为 \(M_i\),求出字符串 \(\left[1,i\right]\) 的哈希值 \(S_i=\prod\limits_{i=1}^nM_i\),求出每个 \(S_i\) 的逆 \(inv_i\),则 \(\prod\limits_{j=l}^{r}M_j=inv_{l-1}S_r\)。
矩阵 \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) 的逆为 \(\begin{bmatrix}d&-c\\-b&a\end{bmatrix}\div(AD-BC)\)。
矩阵 \(A\) 的逆为 \(A\) 的伴随矩阵除以行列式,即 \(A^{-1}=\frac{A^*}{\left|A\right|}\)。
伴随矩阵求法 \(A^*_{i,j}\)
矩阵求逆使用高斯消元。
正确率
一个 \(2\times2\) 的矩阵哈希的正确率和四模的多项式哈希基本是一样的。
例:
给定串 \(S\),\(q\) 次询问,每次询问两个位置 \(l_1\),\(l_2\) 的最长公共前缀。
sol:复杂度允许的情况下,二分+hash 即可。
使用hash的一个要点是找到一种表示。
KMP
不要定义 next,会与某些库里的变量重名引起 CE。
KMP 通过求出一个存储最长相同前缀后缀长度(其中的前缀和后缀不能是整个字符串)的数组 nxt,然后利用 nxt 实现 \(O(n)\) 时间复杂度的求一个字符串 \(T\) 在另一个字符串 \(S\) 中的出现次数。
求 nxt 数组
求的是 \(T\) 的 nxt。
-
显然
nxt[1]为 \(0\)。 -
剩下的
nxt[i]都可以由nxt[i-1]求解得到。
我们已经求出了 \(S_{1,\dots,i-1}\) 的最长相同前缀后缀长度nxt[i-1],如果 \(S_{nxt[i-1]+1}\) 与 \(S_i\) 相等则nxt[i]为nxt[i-1]+1,即在这个长度的基础上匹配成功。
如果没有匹配成功的话,我们需要退到比这个次长的长度,即nxt[nxt[i-1]](等会会在底下证明),继续在这个长度的基础上匹配,如果再匹配不上再退到比这个次长的长度,以此类推,直到匹配成功或匹配失败(即最后一个字符不能和第一个字符匹配)。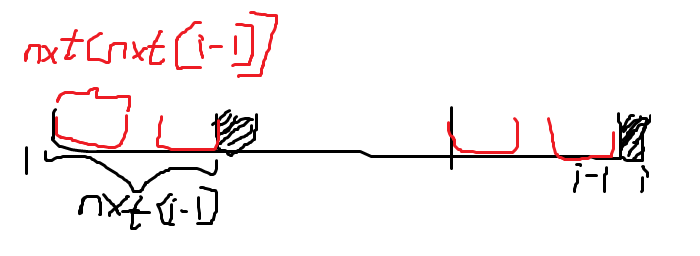
nxt[nxt[i]]为 \(S_{1,\dots,i}\) 次长的相同前缀后缀长度的证明:反证法:设
nxt[nxt[i]]不为次长的相同前缀后缀长度,则会有比其更长的长度 \(x\)。
由于nxt[i]为 \(S_{1,\dots,i}\) 的最长相同前缀后缀长度,所以 \(S_{1,\dots,nxt[i]}\) 与 \(S_{i-nxt[i]+1,\dots,i}\) 相等。
因为有相同前缀后缀长度 \(x\) 存在,所以 \(S_{1,\dots,x}\) 与 \(S_{i-x+1,\dots,i}\) 相等。(图中两端的红色部分)
所以 \(S_{1,\dots,x}\) 与 \(S_{nxt[i]-x+1,\dots,nxt[i]}\) 相等。(图中左侧两块红色部分)
所以 \(x\) 也为 \(S_{1,\dots,nxt[i]}\) 的相同前缀后缀长度之一,但nxt[nxt[i]]大于其不符合最长相同前缀后缀长度的定义,该假设不成立。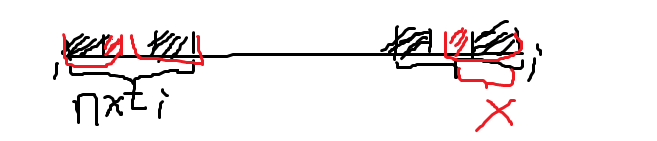
更直观点的想法是,假设已知这个相同前缀后缀长度 \(x\),则一定会满足其等于
nxt[nxt[i]]。
匹配
求出 nxt 后,就匹配 \(T\) 了。
先来扯一下暴力求解。
暴力求解就是枚举字符串的开头的位置,然后一个字符一个字符挨着匹配,这样的最坏的时间复杂度是 \(O(\left|S\right|\left|T\right|)\) 的。
假设在两个开头位置为 \(i\),\(j\) 时匹配成功了(分别为下图的红色和黄色部分),且这两个匹配成功的子串有重叠,显然重叠的部分相等,也就是存在长度为 \(\left|T\right|-(j-i)\) 的相同前缀后缀(如下图的绿色部分)。
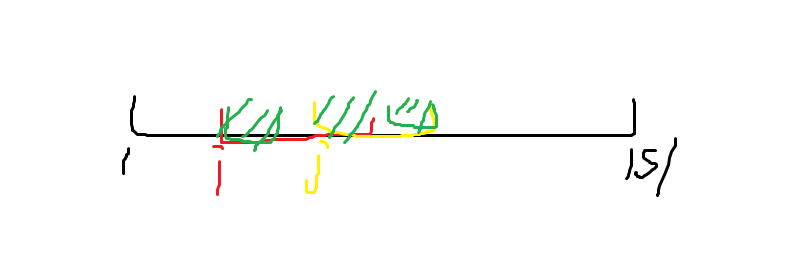
由此可以得出一个相反的结论,只要没有长度为 \(x\) 的相同前缀后缀,那么对于任意匹配成功的开头位置 \(i\),开头位置 \(j=i+\left|T\right|-x\) 的子串与 \(T\) 是不匹配的。
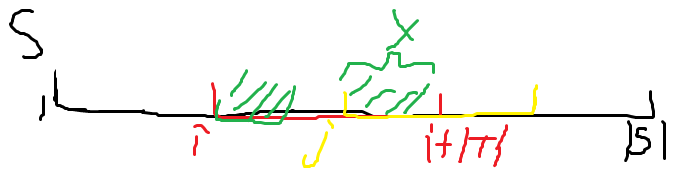
所以我们根据求出的 nxt 可以得知,对于匹配成功的 \(i\),下一个匹配成功的开头位置最近也只能为 \(i+\left|T\right|-nxt[\left|T\right|]\) ( \(nxt[\left|T\right|]\) 即上面的 \(x\) 的最大的情况)。
如果是将匹配了一半的 \(T\) 的子串看做上面的 \(T\) 的话,同样也是成立的。
于是我们可以用 nxt 数组来优化这个匹配的过程,这就是 KMP 算法。
假设当前已经匹配成功了 \(x\) 个字符,\(S\) 匹配的子串开头位置为 \(i\)。
下一步应该比较 \(S_{i+x}\) 与 \(T_{x+1}\)。
- 匹配成功则匹配的长度加 \(1\),假如加 \(1\) 后的长度即 \(T\) 的长度,则 \(T\) 成功匹配,答案加 \(1\),匹配的长度变为 \(nxt[\left|T\right|]\)。
- 如匹配失败,则匹配的长度变为 \(nxt_x\),继续匹配,直至匹配成功或匹配失败。
时间复杂度
对于 KMP 的时间复杂度,对 \(S\) 扫一遍是 \(O(n)\) 的,因为 \(x\) 从 \(\left|T\right|\) 每次减 \(1\) 跳到 \(0\),而扫每个字符时 \(x\) 最多增加 \(1\),所以均摊下来时间复杂度是 \(O(n)\) 的。
洛谷模板代码:
#include<bits/stdc++.h>
using namespace std;
const int MAXLEN=1e6+10;
char s1[MAXLEN],s2[MAXLEN];
int nxt[MAXLEN];
namespace sol{
void solve(){
scanf("%s%s",s1+1,s2+1);
int s2n=strlen(s2+1),p=0;
for(int i=2;i<=s2n;++i){
while(s2[i]!=s2[p+1]&&p)p=nxt[p];
if(s2[i]==s2[p+1]){
nxt[i]=++p;
}
}
int s1n=strlen(s1+1);
p=0;
for(int i=1;i<=s1n;++i){
while(s1[i]!=s2[p+1]&&p)p=nxt[p];
if(s1[i]==s2[p+1]){
++p;
}
if(p==s2n)printf("%d\n",i-p+1);
}
for(int i=1;i<=s2n;++i)printf("%d ",nxt[i]);
}
}
int main(){
sol::solve();
return 0;
}
扩展 KMP(Z 函数)
用类似 Manacher 的对称来做到 KMP 的作用,这何尝不是一种 ntr
给定字符串 \(S\),\(T\),求 \(S\) 的每个后缀与 \(T\) 的最长公共前缀。
设 z[i] 数组表示 \(T_i\) 为开头的 \(T\) 串后缀与 \(T\) 的最长公共前缀。
求 z[i]
显然 z[1] 为 \(\left|T\right|\)。
从 z[2] 开始放循环里求。
假设当前需要求出 z[i],已经求得 z[1] 至 z[i-1]。
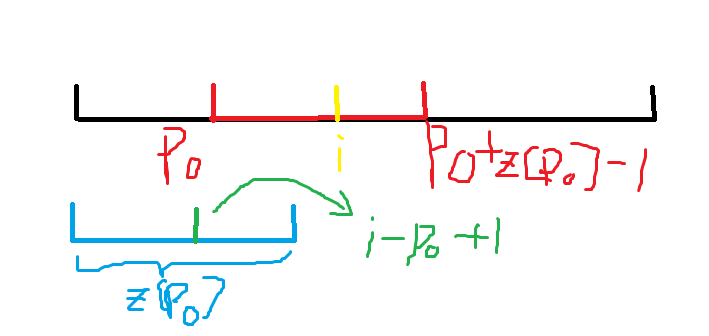
我们可以求得一个 \(p_0\),使得 p0+z[p0]-1 (下图红色部分的右端点,即以 \(p_0\) 为起点的后缀可以匹配到的最后一个字符的位置)最大。
我们知道 \(T_{p_0,\dots,p_0+z[p_0]-1}\) 与 \(T_{1,\dots,z[p_0]}\) 是相等的。
因此 \(T_{i,\dots,p_0+z[p_0]-1}\) 与 \(T_{i-p_0+1,\dots,z[p_0]}\) 也是相等的,可以让 z[i] 赋值为 min(z[p0]+p0-i-1,z[i-p0+1]),剩余的部分由于信息不足无法直接判断,暴力匹配求解后更新 \(p_0\)。
匹配
匹配跟上面求 z[i] 的过程非常像。
实际上我直接贺了上面的部分(包括图),然后稍微改了改。
类似的,像上面 KMP 一样先考虑一下暴力匹配,在此基础上优化。
设从 \(S_i\) 开始的 \(S\) 串的后缀匹配 \(T\) 串的最长长度为 \(p_i\)。
p[1] 可以单独拿出来求,但是边界问题做好的话也可以放循环里面。
假设当前需要求出 p[i],已经求得 p[1] 至 p[i-1]。
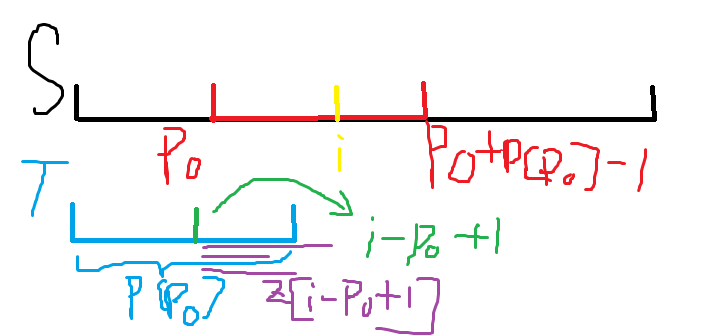
我们可以求得一个 \(p_0\),使得 p0+p[p0]-1 (下图红色部分的右端点,即以 \(p_0\) 为起点的后缀可以匹配到的最后一个字符的位置)最大。
我们知道 \(S_{p_0,\dots,p_0+p[p_0]-1}\) 与 \(T_{1,\dots,p[p_0]}\) 是相等的。
因此 \(S_{i,\dots,p_0+p[p_0]-1}\) 与 \(T_{i-p_0+1,\dots,p[p_0]}\) 也是相等的,我们在前面已经求出了与 \(S_i\) 对应的 \(T_{i-p_0+1}\) 的 z[i-p0+1] (下图绿点的 \(z\) 值,紫色线段为可能的长度),所以 \(S_{i,\dots,\min(p_0+p[p_0]-1,i+z[i-p0+1]-1)}\) 与 \(T_{1,\min(p_0+p[p_0]-i,z[i-p_0+1])}\) 相等,可以让 p[i] 赋值为 min(z[i-p0+1],p0+p[p0]-i),剩余的部分由于信息不足无法直接判断,暴力匹配求解后更新 \(p_0\)。
时间复杂度
由于每次暴力匹配一次会使得 \(p_0\) 加 \(1\),\(p_0\) 最多加到 \(O(n)\),所以时间复杂度均摊下来是 \(O(n)\) 的。
洛谷模板代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
namespace sol{
const int MAXLEN=2e7+10;
char a[MAXLEN],b[MAXLEN];
int z[MAXLEN],p[MAXLEN];
void solve(){
scanf("%s%s",a+1,b+1);
int lena=strlen(a+1),lenb=strlen(b+1);
//z函数部分
z[1]=0;
int p0=1;
ll valz=lenb+1;
for(int i=2;i<=lenb;++i){
z[i]=max(min(z[p0]+p0-i-1,z[i-p0+1]),0);
while(b[i+z[i]]==b[z[i]+1])++z[i];
if(p0+z[p0]<i+z[i])p0=i;
valz^=1ll*(z[i]+1)*i;
}
z[1]=lenb;
printf("%lld\n",valz);
//p数组部分
p0=1;
ll valp=0;
for(int i=1;i<=lena;++i){
p[i]=max(min(z[i-p0+1],p[p0]-(i-p0)),0);
while(i+p[i]<=lena&&p[i]+1<=lenb&&a[i+p[i]]==b[p[i]+1])++p[i];
if(i+p[i]>p0+p[p0])p0=i;
valp^=1ll*(p[i]+1)*i;
}
printf("%lld\n",valp);
}
}
int main(){
sol::solve();
return 0;
}

