dfs序求lca的讲解、相关常见错误及相关问题

本文暂时弃坑，以后会重构。

本文主要是用于警示自己避免犯错。

1|0相关博客

最近公共祖先 | st 表求 lca 别用欧拉序了！！！
冷门科技 —— DFS 序求 LCA

2|0算法讲解

这是以节点 $1$ 为根节点的一棵树

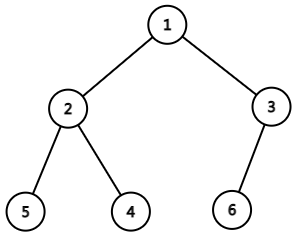
我们在根节点进行 dfs，在 dfs 的开始将到达的节点加入一个序列的末尾中，就得到了所有节点拼成的一个序列，这个序列就是 dfs 序，节点在 dfs 序中的位置被称为节点的 $dfn$ 值。

对这颗树进行 dfs，可求得它的 dfs 序为 $1$,$2$,$4$,$5$,$3$,$6$（dfs 序不唯一，也可能为$1$,$2$,$5$,$4$,$3$,$6$）。节点 $1$ 到 $6$ 的 $dfn$ 值分别为 $1$,$2$,$5$,$3$,$4$,$6$。
得到这个序列有啥用呢？如何求两个节点的 lca？
我们可以观察到某节点的祖先在 dfs 序中一定在该节点的前面，以某节点为根节点的子树的所有子节点（即除根节点外的所有节点）都在根节点的后面。所以不能直接在节点 $u$ 和节点 $v$ 之间找一个节点作为它们的 lca。

我们来分类讨论，从一个简单的情况切入这个问题。
（下面的讨论默认 $df{n}_u$<=$df{n}_v$）

1. $u$ 为 $v$ 的祖先。

还是以上面那个图为例。
我们要找 $1$ 和 $4$ 的 lca，显然 lca 为 $1$。
观察从 $1$ 到 $4$ 的 dfs 序，可以发现整个序列都是在 根节点为 $1$ 的子树上进行的，一定经过 $1$ 的子节点才到达 $4$。
难道是直接返回从 $1$ 到 $4$ 中深度最小的节点吗？
由前面的性质可知某节点的祖先在 dfs 序中一定在该节点的前面，万一 $u$ 不是 $v$ 的祖先，这个方法就完全错了。
我们再回去观察一下。
从 $1$ 到 $4$ 经过了 $1$ 的孩子，也经过了 $4$ 的祖先，$1$ 和 $4$ 的 lca 一定是 $4$ 的祖先，那我们找到 $4$ 的祖先中除去 $1$ 深度最小的那一个的父节点是不是就是 lca？

3|0参考代码

dfs 序求 lca 的参考代码如下。

#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+10,MAXLOG2N=20;
int N,M,S,cnt,head[MAXN],dfn[MAXN],dfncnt,stlca[MAXLOG2N][MAXN],LOG2[MAXN],deep[MAXN],anc[MAXN];
struct EDGE
{
    int v,nxt;
}edge[MAXN<<1];
void add(int u,int v)
{
    ++cnt;
    edge[cnt].v=v;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
}
void dfs(int u)
{
    stlca[0][dfn[u]=++dfncnt]=u;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].v;
        if(v!=anc[u]){anc[v]=u;deep[v]=deep[u]+1;dfs(v);}
    }
}
int deepget(int u,int v)//得到深度浅的节点
{
    return deep[u]<deep[v]?u:v;
}
void stlca_init()
{
    //求解log2部分
    for(int i=2;i<=N;++i){LOG2[i]=LOG2[i>>1]+1;}
    //建ST表部分
    for(int j=1;(1<<j)<=N;++j)
    {
        int temp=N-(1<<j)+1;
        for(int i=1;i<=temp;++i)
        {
            stlca[j][i]=deepget(stlca[j-1][i],stlca[j-1][i+(1<<(j-1))]);
        }
    }
}
int lca(int u,int v)
{
    if(u==v)return u;
    if(dfn[u]>dfn[v])swap(u,v);//保持dfn[u]<dfn[v]
    int k=LOG2[dfn[v]-dfn[u]];
    int lcason=deepget(stlca[k][dfn[u]+1],stlca[k][dfn[v]-(1<<k)+1]);
    return anc[lcason];
}
int main()
{
    ios::sync_with_stdio(0);cin.tie(0);
    cin>>N>>M>>S;
    for(int i=1;i<N;++i)
    {
        int x,y;cin>>x>>y;
        add(x,y);
        add(y,x);
    }
    deep[S]=1;//根节点深度为1好看
    dfs(S);
    stlca_init();
    while(M--)
    {
        int a,b;cin>>a>>b;
        cout<<lca(a,b)<<'\n';
    }
    return 0;
}

4|0常见错误

1. 无向边存储时少一次变成有向边。

太（）（）了。

2. dfs 过程中忘记添加祖先及深度的记录。

void dfs(int u)
{
    stlca[0][dfn[u]=++dfncnt]=u;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].v;
        if(v!=anc[u])dfs(v);
    }
}

这都能写错？？？

3. 查找深度小的节点的函数写错。

int deepget(int u,int v)//得到深度浅的节点
{
    return dfn[u]<dfn[v]?u:v;
}

我晕。

4. ST 表建表写错

for(int j=1;(1<<j)<=N;++j)
{
    for(int i=1;i+(1<<j)-1<=N;++i)
    {
        stlca[j][i]=deepget(stlca[j-1][i],stlca[j-1][i+(1<<j/*应为1<<(j-1)!*/)]);
    }
}

我怎么会在前面的 log 下标填 j-1 后填了个 i+(1<<j)。

5. lca 求解过程中忘了写 u==v 的情况。
6. lca 求解过程中忘了将 $dfn$ 较大的 $u$ 与 $v$ 交换。

这两种情况倒是没写错过，不过以防万一还是加上。

7. 直接把 lcason 返回。

st 表求的是 dfs 序中 $u$ 所在位置加上 $1$ 到 $v$ 的位置中的深度最小的节点，并不是 lca，而是 lca 的孩子。

8. 左移与加法运算的时候不加括号。

stlca[j][i]=deepget(stlca[j-1][i],stlca[j-1][i+1<<(j-1)]);

左移的优先级小于加法，不加括号导致运算的顺序错误，建议多加括号保险

5|0一些问题

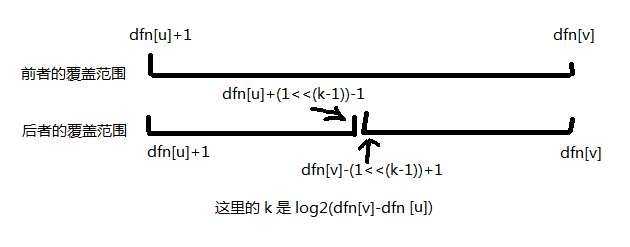
1. 我的 $k$ 在求解过程中写错了，原本应该是下面的代码的前者（dfn[u]+1 到 dfn[v] 这个序列的长度），却写成了后者（序列长度减去 $1$），但是没有被 hack 掉，是怎么回事？

int k=LOG2[dfn[v]-dfn[u]];//前者
int k=LOG2[dfn[v]-(dfn[u]+1)];//后者

可以看出这两种写法有区别当且仅当 dfn[v]-dfn[u] 为 $2$ 的倍数。
此时两种写法虽然 log 下标不同，但可以看出其覆盖范围是相同的。

看的出来，后者写法的两段区间刚好无缝衔接（衔接的两个端点差为 $1$），所以两种写法的输出都是正确的。

6|0后言

写的可能不是很完整，以后可能补充。

__EOF__

本文作者：LiJoQiao
本文链接：https://www.cnblogs.com/LiJoQiao/p/17706287.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！