[CTSC1999]家园

题目描述：

由于人类对自然资源的消耗，人们意识到大约在 2300 年之后，地球就不能再居住了。于是在月球上建立了新的绿地，以便在需要时移民。令人意想不到的是，2177 年冬由于未知的原因，地球环境发生了连锁崩溃，人类必须在最短的时间内迁往月球。

现有 n 个太空站位于地球与月球之间，且有 m 艘公共交通太空船在其间来回穿梭。每个太空站可容纳无限多的人，而每艘太空船 i 只可容纳 H[i]个人。每艘太空船将周期性地停靠一系列的太空站，例如：(1，3，4)表示该太空船将周期性地停靠太空站 134134134…。每一艘太空船从一个太空站驶往任一太空站耗时均为 1。人们只能在太空船停靠太空站(或月球、地球)时上、下船。

初始时所有人全在地球上，太空船全在初始站。试设计一个算法，找出让所有人尽快地全部转移到月球上的运输方案。

对于给定的太空船的信息，找到让所有人尽快地全部转移到月球上的运输方案。

程序运行结束时，将全部人员安全转移所需的时间输出。如果问题无解，则输出 0。

题解：

对于无解，我们可以用并查集维护联通性，只要地球和月球在同一个集里就行了。

剩下的跑分层最大流。

对于如何分层，这里画一下样例：

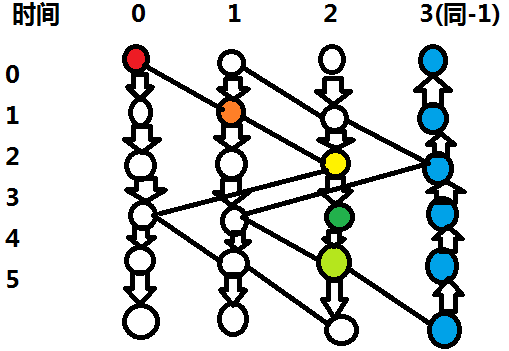
对于每个时间的每个点向下一时间建边，边权无穷大;

对于太空船的运动建边，边权为太空船容量。

一层一层加边，然后在残余网络上直接跑dinic，直到流量之和不小于k。

代码：

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 20
#define M 25
#define K 55
inline int rd()
{
    int f=1,c=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){c=10*c+ch-'0';ch=getchar();}
    return f*c;
}
int fa[N];
int findfa(int x)
{
    if(fa[x]==x)return x;
    return fa[x]=findfa(fa[x]);
}
int n,m,k,hed[100*N],cur[100*N],cnt=-1;
struct ship
{
    int h,r;
    int s[N];
    int fd(int k)
    {
        return s[k%r];
    }
}p[M];
struct EG
{
    int to,vl,nxt;
}e[1000*N];
void ae(int f,int t,int v)
{
    e[++cnt].to = t;
    e[cnt].vl = v;
    e[cnt].nxt = hed[f];
    hed[f] = cnt;
}
int sum = 0,S,T;
const int inf = 0x3f3f3f3f;
int dep[100*N];
bool bfs()
{
    queue<int>q;
    memset(dep,0x3f,sizeof(dep));
    memcpy(cur,hed,sizeof(cur));
    dep[S]=0;
    q.push(S);
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        for(int j=hed[u];~j;j=e[j].nxt)
        {
            int to = e[j].to;
            if(e[j].vl&&dep[to]==inf)
            {
                dep[to]=dep[u]+1;
                q.push(to);
            }
        }
    }
    if(dep[T]!=inf)return 1;
    return 0;
}
int dfs(int u,int lim)
{
    if(!lim||u==T)return lim;
    int fl=0,f;
    for(int j=cur[u];~j;j=e[j].nxt)
    {
        cur[u]=j;
        int to = e[j].to;
        if(dep[to]==dep[u]+1&&(f=dfs(to,min(lim,e[j].vl))))
        {
            fl+=f;
            lim-=f;
            e[j].vl-=f;
            e[j^1].vl+=f;
            if(!lim)break;
        }
    }
    return fl;
}
int dinic()
{
    int ret = 0;
    while(bfs())
        ret+=dfs(S,inf);
    return ret;
}
int main()
{
    n=rd(),m=rd(),k=rd();
    S=0,T=n+1;
    memset(hed,-1,sizeof(hed));
    for(int i=0;i<=n+1;i++)
        fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        p[i].h=rd(),p[i].r=rd();
        int f1=-1,f2=-1;
        for(int j=0;j<p[i].r;j++)
        {
            p[i].s[j]=rd();
            if(p[i].s[j]==-1)p[i].s[j]=n+1;
            if(!j)
            {
                f1=findfa(p[i].s[j]);
            }else
            {
                f2=findfa(p[i].s[j]);
                if(f1!=f2)fa[f2]=f1;
            }
        }
    }
    int f1 = findfa(0);
    if(findfa(n+1)!=f1)
    {
        printf("0\n");
        return 0;
    }
    int ans = 0,f,t,v;
    while(sum<k)
    {
        ans++;
        for(int i=0;i<=n;i++)
        {
            f = (n+2)*(ans-1)+i;
            t = (n+2)*ans+i;
            ae(f,t,inf);
            ae(t,f,0);
        }
        f = (n+2)*(ans+1)-1;
        t = (n+2)*ans-1;
        ae(f,t,inf);
        ae(t,f,0);
        for(int i=1;i<=m;i++)
        {
            f = (n+2)*(ans-1)+p[i].fd(ans-1);
            t = (n+2)*ans+p[i].fd(ans);
            v = p[i].h;
            ae(f,t,v);ae(t,f,0);
        }
        sum+=dinic();
    }
    printf("%d\n",ans);
    return 0;
}