ZJOI2012 小蓝的好友

题目描述：

bz

luogu

题解：

好久不写$treap$了来水一发。

$treap$维护dp。

考虑在这个图上确定一个矩形的三条边，那么至少包含一个关键点的矩形的数量由开口方向的第一个关键点决定。

然后是这样的一个图：

 

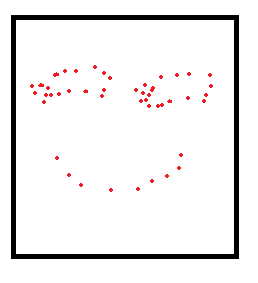
考虑从下往上做扫描线，对于左右下三条边，我们能取的范围是这样的：

这个只是对当前的左右下来说的。

扩展一下，还有这样的：

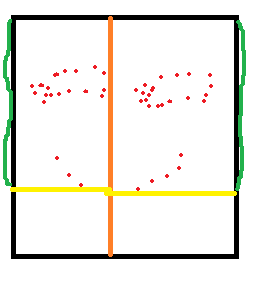
这个过程像是堆的遍历。

考虑动态维护这个堆，发现不会……

但是善良的出题人写了：

所以位置是随机的=v=

所以直接$Treap$维护这个大根堆+左右区间个数了=v=

同时这个图还有一个性质，就是定住$x$改变$y$时$y$只会变大。

所以$Treap$在修改的时候节点只会向上转=v=

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 100050;
const int M = 40050;
template<typename T>
inline void read(T&x)
{
    T f = 1,c = 0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){c=c*10+ch-'0';ch=getchar();}
    x = f*c;
}
struct Point
{
    ll x,y;
    Point(){}
    Point(ll x,ll y):x(x),y(y){}
    bool operator < (const Point&a)const{return x!=a.x?x<a.x:y<a.y;}
}p[N];
ll r,c,n;
struct Treap
{
    int rt,ls[M],rs[M],siz[M];
    ll w[M],k[M];
    void update(int u)
    {
        siz[u] = siz[ls[u]]+siz[rs[u]]+1;
        w[u] = k[u]*(siz[ls[u]]+1)*(siz[rs[u]]+1)+w[ls[u]]+w[rs[u]];
    }
    void lturn(int&u)
    {
        int t = rs[u];rs[u] = ls[t];
        ls[t] = u;siz[t] = siz[u];
        update(u),update(t);u = t;
    }
    void rturn(int&u)
    {
        int t = ls[u];ls[u] = rs[t];
        rs[t] = u;siz[t] = siz[u];
        update(u),update(t);u = t;
    }
    void chg(int&u,int qx,ll qw)
    {
        if(!u)return ;
        if(u==qx)
        {
            k[u] = qw;
            update(u);
            return ;
        }
        if(qx<u)
        {
            chg(ls[u],qx,qw);
            if(k[u]<k[ls[u]])rturn(u);
        }else
        {
            chg(rs[u],qx,qw);
            if(k[u]<k[rs[u]])lturn(u);
        }
        update(u);
    }
    void build(int l,int r,int&u)
    {
        if(l>r)return ;
        u = (l+r)>>1;
        build(l,u-1,ls[u]);
        build(u+1,r,rs[u]);
        update(u);
    }
}tr;
int main()
{
    read(r),read(c),read(n);
    for(int i=1;i<=n;i++)
        read(p[i].x),read(p[i].y);
    tr.build(1,c,tr.rt);
    sort(p+1,p+1+n);
    ll ans = 0;
    for(int i=1,j=1;i<=r;i++)
    {
        while(j<=n&&p[j].x==i)tr.chg(tr.rt,p[j].y,i),j++;
        ans += tr.w[tr.rt];
    }
    printf("%lld\n",ans);
    return 0;
}