三倍经验——bzoj3663、4660、4206 Crazy Rabbit/最大团

题目描述：

3663

4660

4206

题解：

第一眼：不成立的互相连边，然后用网络流求解无向图最小点覆盖！

好吧我不会。

正解：

每个点对应圆上的一段圆弧，长这样：

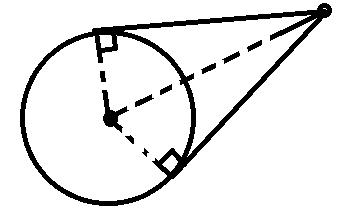
设对应圆弧$(l,r)$。

若$[a,b]$可以同时选中，那么$la<lb<ra<rb$（或者二者调换）。

还有一点是，优弧=劣弧。这个自己手画一下应该会更清楚。

所以将$[a,b]$限制在$[-Pi,Pi]$内，问题转化为求最长的$la<lb<……<lk<ra<rb<……<rk$。

先按$l$排序，枚举$a$，把合法的$rb……rk$都扔到数组里，最后跑一遍最长上升子序列。

时间复杂度$O(n^2logn)$

代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2050;
const double Pi = acos(-1.0);
const double eps = 1e-8;
int dcmp(double x)
{
    if(fabs(x)<=eps)return 0;
    return x>0?1:-1;
}
template<typename T>
inline void read(T&x)
{
    T f = 1,c = 0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){c=c*10+ch-'0';ch=getchar();}
    x = f*c;
}
int n,x[N],y[N],tl,ans,t;
struct node
{
    double x,y;
    node(){}
    node(double x,double y):x(x),y(y){}
    bool operator < (const node&a)const{return dcmp(x-a.x)?dcmp(x-a.x)<0:dcmp(y-a.y)<0;}
}p[N];
double r,sta[N],s[N];
void fix(double x)
{
    int l = 1,r = t,k = t;
    while(l<=r)
    {
        int mid = (l+r)>>1;
        if(s[mid]>x)k=mid,r=mid-1;
        else l=mid+1;
    }
    s[k] = x;
}
void LIS()
{
    t = 0;
    for(int i=1;i<=tl;i++)
        if(!t||sta[i]>s[t])s[++t]=sta[i];
        else fix(sta[i]);
    ans = max(ans,t);
}
int main()
{
//  freopen("crazy.in", "r", stdin);
//  freopen("crazy.out", "w", stdout);
//  freopen("tt.in","r",stdin);
    read(n),read(r);
    for(int i=1;i<=n;i++)
    {
        read(x[i]),read(y[i]);
        double bas = atan2(y[i],x[i]);
        double dlt = acos(r/sqrt(x[i]*x[i]+y[i]*y[i]));
        p[i].x = bas-dlt,p[i].y = bas+dlt;
        if(p[i].x<-Pi)p[i].x+=2*Pi;
        if(p[i].y>Pi)p[i].y-=2*Pi;
        if(p[i].x>p[i].y)swap(p[i].x,p[i].y);
    }
    sort(p+1,p+1+n);
    for(int i=1;i<=n;i++)
    {
        tl=0;
        for(int j=i+1;j<=n&&p[j].x<=p[i].y;j++)
            if(p[j].y>p[i].y)sta[++tl]=p[j].y;
        LIS();
    }
    printf("%d\n",ans+1);
    return 0;
}