计算几何模板（3）：圆

现在让我们来说说圆……

1.圆

貌似只有圆心+半径是人类可用的……

我们还可以知道圆上任一角度点的坐标。

struct Circle
{
    Point p;
    double r;
    Circle(){}
    Circle(Point p,double r):p(p),r(r){}
    Point point(double rad){return Point(p.x+r*cos(rad),p.y+r*sin(rad));}
};

2.直线与圆交点

显然三种情况：

圆心到直线距离>半径，此时没有交点；

圆心到直线距离=半径，此时交点为垂足；

圆心到直线距离<半径，此时交点有两个：

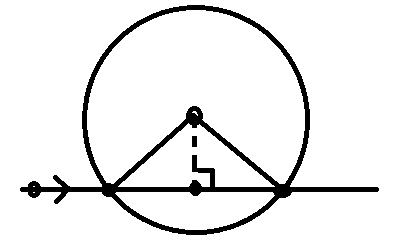
现在我们已知直角边=半径，一条直角边=圆心到直线距离，那么另一条直角边边长可求，搞出高线法向量即可。

int L_C(Line l,Circle c,vector<Point>&ve)
{
    Point p = c.p;double r = c.r,dis = Dis_P_L(p,l);
    if(dcmp(dis-r)>0)return 0;
    else if(!dcmp(dis-r))
    {
        ve.push_back(P_L(p,l));
        return 1;
    }
    Point h = P_L(p,l);Vector tmp = Nol(h-p);
    double len = sqrt(r*r-dis*dis);
    ve.push_back(h+tmp*len);
    ve.push_back(h-tmp*len);
    return 2;
}

3.圆与圆交

分好几种情况：

圆心重合，若半径相同则无数条，半径不同则无交点；

圆心不重合，若相离则无交点；

然后：

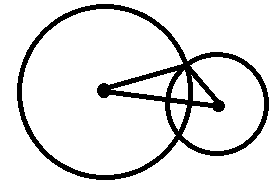
我们惊奇地发现三角形三边都已知，那么暴力余弦定理可求得夹角。

int C_C(Circle a,Circle b,vector<Point>&ve)
{
    double dis = lth(a.p-b.p);
    if(!dcmp(dis))
    {
        if(!dcmp(a.r-b.r))return -1;
        return 0;
    }
    if(dcmp(a.r+b.r-dis)<0)return 0;
    double rad = ang(b.p-a.p);
    double dlt = acos((a.r*a.r+dis*dis-b.r*b.r)/(2*a.r*dis));
    Point p1 = a.point(rad+dlt),p2 = a.point(rad-dlt);
    if(p1==p2)
    {
        ve.push_back(p1);
        return 1;
    }else
    {
        ve.push_back(p1);
        ve.push_back(p2);
        return 2;
    }
}

4.过顶点作圆的切线

三种情况：

点在圆内，此时无切线；

点在圆上，此时切线与两点连线垂直；

点在圆外，就是：

然后直接得到夹角。

int T_P_C(Circle c,Point p,vector<Vector>&ve)
{
    Vector v = c.p-p;
    double dis = lth(v);
    if(!dcmp(dis-c.r))
    {
        ve.push_back(Vector(-v.y,v.x));
        return 1;
    }else if(dcmp(dis-c.r)<0)return 0;
    double rad = asin(c.r/dis);
    ve.push_back(rot(v,rad));
    ve.push_back(rot(v,-rad));
    return 2;
}

5.两圆公切线

情况比较多。

设几个变量，$dis$表示圆心距离，$rd$表示半径之差，$rs$表示半径之和。

首先，判一下圆心重合。

然后公切线有两种，外公切线和内公切线：

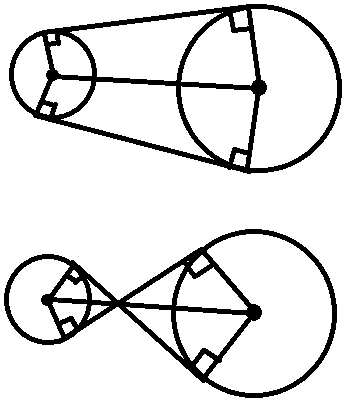
外公切线从无到有的临界是这样的：

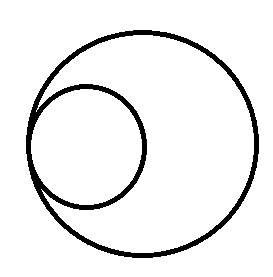
这个时候$dis=rd$，一条公切线。

然后是：

两条外公切线，没有内公切线。

再动一动：

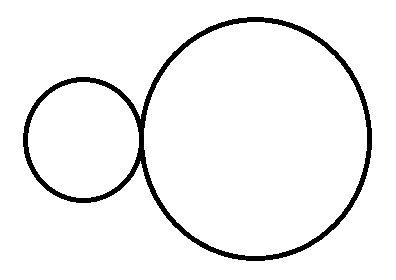
两条外公切线，一条内公切线。

此时$dis=rs$。

最后：

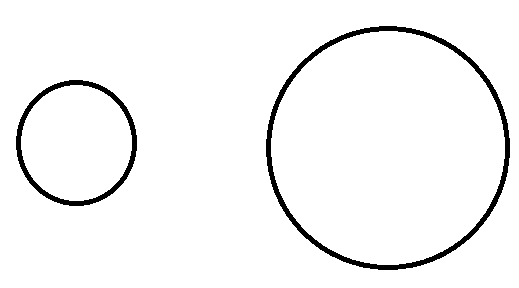
两条外公切线，两条内公切线。

现在回到怎么求的问题上。

辅助线：

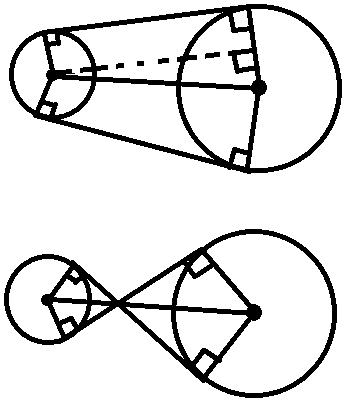
外公切线用$rd$与$dis$求，内公切线用$rs$与$dis$求。

int T_C_C(Circle a,Circle b,vector<Point>&pa,vector<Point>&pb)
{
    if(a.r>b.r)swap(a,b),swap(pa,pb);
    double dis = lth(a.p-b.p),rd = fabs(a.r-b.r),rs = a.r+b.r;
    if(dcmp(dis-rd)<0)return 0;
    if(!dcmp(dis)&&!dcmp(a.r-b.r))return -1;
    double rad = ang(b.p-a.p);
    if(!dcmp(dis-rd))
    {
        pa.push_back(a.point(rad)),pb.push_back(b.point(rad));
        return 1;
    }
    double drad = acos(rd/dis);
    pa.push_back(a.point(rad+drad)),pb.push_back(b.point(rad+drad));
    pa.push_back(a.point(rad-drad)),pb.push_back(b.point(rad-drad));
    if(!dcmp(dis-rs))
    {
        pa.push_back(a.point(rad)),pb.push_back(b.point(-rad));
        return 3;
    }else if(dcmp(dis-rs)>0)
    {
        drad = acos(rs/dis);
        pa.push_back(a.point(rad+drad)),pb.push_back(b.point(rad-drad));
        pa.push_back(a.point(rad-drad)),pb.push_back(b.point(rad+drad));
        return 4;
    }else return 2;
}