计算几何模板（2）：线与线

比点与向量部分要难一点，会有一定的技巧与证明。

---

 

1.首先是直线。

小学生都知道两点确定一条直线。

所以我们不用两点式，用点斜式。

一个直线上的点+一个向量=一条直线。

struct Line
{
    Point x;
    Vector v;
    Line(){}
    Line(Point x,Vector v):x(x),v(v){}
};

2.两直线求交点

我们知道两直线是这样的：

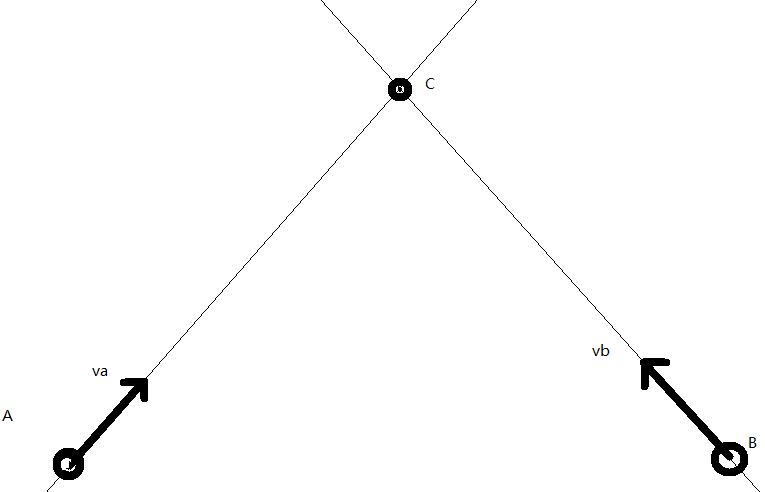
求点$C$。

现在来做几条辅助线：

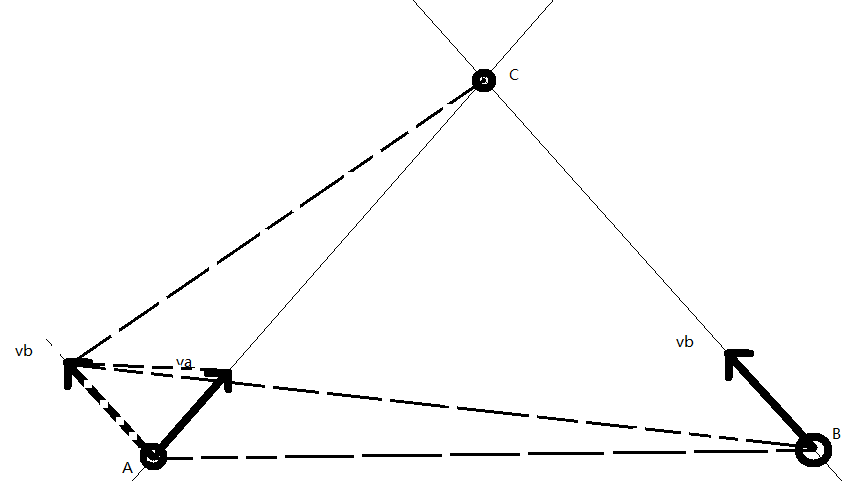
现在新产生了三个三角形，两大一小。

两个大的面积相等，因为同底等高。

所以面积可求，$AC$可求。

Point L_L(Line a,Line b)
{
    double t = (b.v^(b.x-a.x))/(b.v^a.v);
    return a.x+a.v*t;
}

 3.点到直线距离

有标准式方程就可以套公式了，但是我们只有（假的）点斜式。

其实更简单，搞个三角形叉积求面积，然后求高就好了。

就像这样：

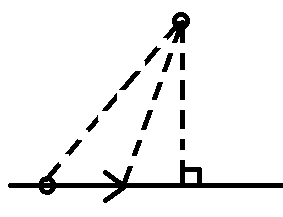
（叉积求的是有向面积，结果要加绝对值）

double Dis_P_L(Point p,Line l)
{
    return fabs((l.v^(p-l.x))/lth(l.v));
}

4.点到线段

（线段直接用端点给出）

端点处有钝角=垂足不在线段上。

钝角直接用$sin$值判。

double Dis_P_S(Point p,Point a,Point b)
{
    if(a==b)return lth(p-a);
    Vector v1 = b-a,v2 = p-a,v3 = p-b;
    if(v1*v2<=0)return lth(v2);
    else if(v1*v3>=0)return lth(v3);
    else return (v1^v2)/lth(v1);
}

5.过定点求直线垂足（非人语

依然是面积法，与上面那个差不多（？）就不证了。

Point P_L(Point p,Line l)
{
    return l.p+l.v*(((p-l.x)*l.v)/(l.v*l.v));
}

6.线段是否相交（交点不在端点上）

相交和不相交：

然后连起来：

所以判对于任意一条线段，另一条线段的两端点是否在其两侧即可。

bool S_S(Point a1,Point a2,Point b1,Point b2)
{
    double d1 = (a2-a1)^(b1-a1),d2 = (a2-a1)^(b2-a1);
    double d3 = (b2-b1)^(a1-b1),d4 = (b2-b1)^(a2-b1);
    return dcmp(d1)*dcmp(d2)<0&&dcmp(d3)*dcmp(d4)<0;
}

7.点在线段上（不能在端点上）

叉积判点在直线上，点积判端点在其两侧。

bool P_S(Point p,Point a,Point b)
{
    Vector A = a-p,B = b-p;
    return dcmp(A*B)==0&&dcmp(A^B)<0;
}