bzoj3336 Uva10572 Black and White
题目描述:

数据范围:2<=n,m<=8
题解:
很明显需要状压。但是怎么压不知道,压什么不知道。
然后从条件下手。
条件1要求黑色在一起白色在一起,记录轮廓线很容易做到。
条件2要求不能出现$2*2$的同色方格。我们还需要再记录当前位置的左上角。
所以这道题的轮廓线长这样。
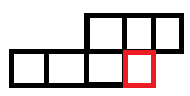
丑图。
我们需要确定一个顺序记录哪几块互相联通。由于轮廓线奇特的形状我决定这样标号。
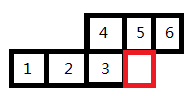
如果编号相同但是并不互相联通我们可以知道他俩不同颜色。
为了颜色我们决定记录某个块的颜色,这样可以得到所有颜色。
于是这道题表中存的就是$1$号颜色+所有状态。
为了方便调试我用了十进制。
每次调用时都要解压,处理后压缩放回去。
由于第一行和第一列找不到长这样的轮廓线,我们可以搜出第一行所有状态,处理第一列时直接枚举黑色/白色。
接下来就是精彩的特判环节。
(这一部分针对处于中心部位的一干普通点)
以填黑色为例。
如果这里不能填黑:
1.输入要求白色。
2.拐角处已经有三个黑块。
3.要考虑到上图中红块填上后$5$号块就不再与不定颜色相邻,我们不能把$5$号块憋死我们要判断$5$号是否有与之联通的好朋友在轮廓线上。
类似围棋中的气。
如果没有而且$5$号是白的,那么就不能填黑!
等等好像是错的。
如果红块已经到$(n,m-1)$或者是$(n,m)$,而且轮廓线上其他都是黑的,我们可以放黑色。
所以这又是个特判。
4.对于3我们考虑的是上下断开,能否出现左右断开?
当然可能。
但是只能在最后一行出现。
所以统计答案时要填回去看一眼。
真 恶心。
深思熟虑后糊上去的代码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define N 15 #define ll long long int T,n,m,k,a[N][N]; char ch[N][N]; ll bas[N],ans; struct Map { int hed[1000050],cnt[2]; struct EG { int nxt; ll to,w; }e[2000050][2]; void ae(int f,ll t,ll w) { e[++cnt[k]][k].to = t; e[cnt[k]][k].nxt = hed[f]; e[cnt[k]][k].w = w; hed[f] = cnt[k]; } void push(ll u,ll w) { for(int j=hed[u%1000000];j;j=e[j][k].nxt) if(e[j][k].to==u) { e[j][k].w += w; return ; } ae(u%1000000,u,w); } void clear() { cnt[k] = 0; memset(hed,0,sizeof(hed)); } }mp; int col[N],grp[N],tmp[N],las[N]; ll zip() { ll ret = 0; for(int i=1;i<=m+1;i++)ret=10*(ret+grp[i]); return ret+col[1]; } void upz(ll u) { memset(tmp,-1,sizeof(tmp)); tmp[1]=u%10;u/=10; for(int i=m+1;i>=1;i--,u/=10)grp[i]=u%10; for(int i=1;i<=m+1;i++) if(tmp[grp[i]]==-1)tmp[grp[i]]=tmp[grp[i-1]]^1; for(int i=1;i<=m+1;i++) col[i]=tmp[grp[i]]; } void shake()//get the express { memset(tmp,0,sizeof(tmp)); for(int cnt=0,i=1;i<=m+1;i++) if(!tmp[grp[i]])tmp[grp[i]]=++cnt; for(int i=1;i<=m+1;i++)grp[i]=tmp[grp[i]]; } bool find_friend(int now,int beg,int ens) { int cnt = 0; for(int i=beg;i<=ens;i++) if(grp[i]==now)cnt++; return cnt>0; } bool ck1() { for(int i=1;i<=m;i++) if(col[i]+a[1][i]==1)return 0; return 1; } bool ck2() { int cnt = 0; for(int i=2;i<=m;i++) cnt+=(col[i]!=col[i-1]); return cnt<=2; } int ck3(int c) { if(col[m-1]==col[m]&&col[m]==col[m+1]&&col[m+1]==c)return 0; int c0 = col[m],ret=1; for(int i=1;i<=m+1;i++)las[i]=grp[i]; col[m] = c;grp[m] = m+2; if(col[m-1]==c) { int kg = grp[m-1]; for(int i=1;i<=m+1;i++)if(grp[i]==kg)grp[i]=m+2; } if(col[m+1]==c) { int kg = grp[m+1]; for(int i=1;i<=m+1;i++)if(grp[i]==kg)grp[i]=m+2; } shake(); for(int i=1;i<=m+1;i++)if(grp[i]>2)ret = 0; for(int i=1;i<=m+1;i++)grp[i] = las[i]; if(col[m-1]==c) { int kg = grp[m-1]; for(int i=1;i<=m+1;i++)if(grp[i]==kg)grp[i]=m+2; } if(col[m+1]==c) { int kg = grp[m+1]; for(int i=1;i<=m+1;i++)if(grp[i]==kg)grp[i]=m+2; } shake(); for(int i=1;i<=m+1;i++)if(grp[i]>2)ret = 0; for(int i=1;i<=m+1;i++)grp[i]=las[i]; col[m] = c0; return ret; } void PushF() { for(int i=0;i<(1<<m);i++) { for(int j=1;j<=m;j++)col[j]=(i>>(j-1))&1; if(!ck1())continue; if(!ck2())continue; grp[1]=1; for(int j=2;j<=m+1;j++)if(col[j]==col[j-1])grp[j]=grp[j-1];else grp[j]=grp[j-1]+1; mp.push(zip(),1); } } bool check_b(int i,int j) { if(a[i][j]==0)return 0; if(col[j-1]==1&&col[j]==1&&col[j+1]==1)return 0; if((i!=n||j!=m)&&(i!=n||j!=m-1)) if(col[j+1]==0&&!find_friend(grp[j+1],j+2,m+1)&&!find_friend(grp[j+1],1,j-1)) return 0; return 1; } bool check_w(int i,int j) { if(a[i][j]==1)return 0; if(col[j-1]==0&&col[j]==0&&col[j+1]==0)return 0; if((i!=n||j!=m)&&(i!=n||j!=m-1)) if(col[j+1]==1&&!find_friend(grp[j+1],j+2,m+1)&&!find_friend(grp[j+1],1,j-1)) return 0; return 1; } int main() { // freopen("tt.in","r",stdin); scanf("%d",&T); bas[0]=1; for(int i=1;i<=10;i++)bas[i] = 10*bas[i-1]; while(T--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%s",ch[i]+1); for(int j=1;j<=m;j++) { if(ch[i][j]=='o')a[i][j]=0; else if(ch[i][j]=='#')a[i][j]=1; else a[i][j]=2; } } ans=0,k=0,mp.clear(); PushF(); for(int i=2;i<=n;i++) { k^=1;mp.clear(); for(int j=1;j<=mp.cnt[!k];j++) { ll now = mp.e[j][!k].to,val = mp.e[j][!k].w; upz(now); for(int o=m+1;o>=2;o--)grp[o]=grp[o-1],col[o]=col[o-1]; for(int q=1;q<=m+1;q++)las[q]=grp[q]; if(a[i][1]!=0)//black { if(col[2]==1) { col[1]=1,grp[1]=grp[2]; shake(); mp.push(zip(),val); }else { if(find_friend(grp[2],3,m+1)) { col[1]=1,grp[1]=m+2; shake(); mp.push(zip(),val); }else if(i==n&&m==2) { col[1]=1,grp[1]=m+2; shake(); mp.push(zip(),val); } } } for(int q=1;q<=m+1;q++)grp[q]=las[q]; if(a[i][1]!=1)//white { if(col[2]==0) { col[1]=0,grp[1]=grp[2]; shake(); mp.push(zip(),val); }else { if(find_friend(grp[2],3,m+1)) { col[1]=0,grp[1]=m+2; shake(); mp.push(zip(),val); }else if(i==n&&m==2) { col[1]=0,grp[1]=m+2; shake(); mp.push(zip(),val); } } } } for(int j=2;j<=m;j++) { k^=1,mp.clear(); for(int o=1;o<=mp.cnt[!k];o++) { ll now = mp.e[o][!k].to,val = mp.e[o][!k].w; upz(now);int c0 = col[j]; if(i==n&&j==m) { if(n==2&&m==2) { if(col[1]==col[3]) { if((a[n][m]==2||a[n][m]!=col[1])&&col[2]==col[1]) ans+=val*ck3(col[1]^1); else if((a[n][m]==2||a[n][m]==col[1])&&col[2]!=col[1]) ans+=val*ck3(col[1]); }else { if(a[n][m]==2)ans+=val*(ck3(0)+ck3(1)); else ans+=val*ck3(a[n][m]); } }else { if(col[m-1]==col[m+1]) { if(a[n][m]==2||a[n][m]==col[m-1]) ans+=val*ck3(col[m-1]); }else { if(a[n][m]==2)ans+=val*(ck3(0)+ck3(1)); else ans+=val*ck3(a[n][m]); } } continue; } if(check_b(i,j))//black { col[j]=1;grp[j]=m+2; for(int q=1;q<=m+1;q++)las[q]=grp[q]; if(col[j-1]==1) { int kg = grp[j-1]; for(int q=1;q<=m+1;q++)if(grp[q]==kg)grp[q]=m+2; } if(col[j+1]==1) { int kg = grp[j+1]; for(int q=1;q<=m+1;q++)if(grp[q]==kg)grp[q]=m+2; } shake(); if(i==n&&j==m)ans+=val; mp.push(zip(),val); for(int q=1;q<=m+1;q++)grp[q]=las[q]; } col[j] = c0; if(check_w(i,j))//white { col[j]=0;grp[j]=m+2; if(col[j-1]==0) { int kg = grp[j-1]; for(int q=1;q<=m+1;q++)if(grp[q]==kg)grp[q]=m+2; } if(col[j+1]==0) { int kg = grp[j+1]; for(int q=1;q<=m+1;q++)if(grp[q]==kg)grp[q]=m+2; } shake(); if(i==n&&j==m)ans+=val; mp.push(zip(),val); } } } } printf("%lld\n",ans); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号