HNOI2011 括号修复

题目描述

题解：

首先，任意一个括号序列消去成对括号后一定是‘)))……)(……(((’的形式。

如果我们能求出当前子序列消去后剩下的东西长什么样，我们就能O(1)出解。

比如前面有a个')'，后面有b个‘(’。

那么$ans = (a+1)/2 + (b+1)/2$.

建议自己画一画。

现在的问题是怎么修改。

splay支持区间翻转，考虑用splay维护。

这里引入我的构造想法，不知道有没有人用：

将')''('分别作为：

这样串$))(((((())))$可表示为：

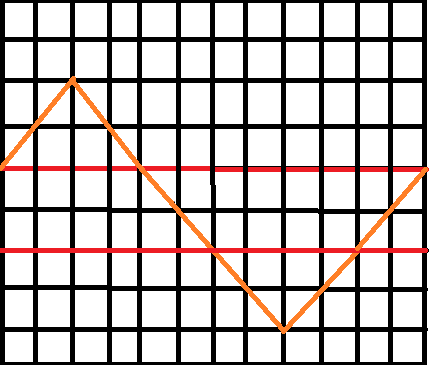
我们可以发现，剩余的')'就是正向看的最大向上高度，'('就是反向看的最大向下高度。

所以我们要维护这两个值。

这样replace和swap操作可以解决。

那么invert呢？

就是让这个图形上下倒过来画咯。

所以我们还要维护最小向上/向下高度。

所以总结一下：

swap:交换两个最大、交换两个最小；

invert:交换两个正向看的值并变成相反数、交换两个反向看的值并变成相反数；

replace:区间赋值，重要的是清invert标记！！！

然后代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100050
int n,m;
char s[N];
struct Splay
{
    int fa[N],ch[N][2],siz[N],rt,rep[N];
    bool swa[N],inr[N];
    int v[N],f[N][2],g[N][2],tag[N],sum[N];//max/min front max/min back
    void update(int u)
    {
        int ls = ch[u][0],rs = ch[u][1];
        siz[u] = siz[ls]+siz[rs]+1;
        sum[u] = sum[ls]+sum[rs]+v[u];
        f[u][0] = max(f[ls][0],sum[ls]+v[u]+f[rs][0]);
        f[u][1] = min(f[ls][1],sum[ls]+v[u]+f[rs][1]);
        g[u][0] = max(g[rs][0],sum[rs]+v[u]+g[ls][0]);
        g[u][1] = min(g[rs][1],sum[rs]+v[u]+g[ls][1]);
    }
    void Swap(int u)
    {
        if(!u)return ;
        swa[u]^=1;
        swap(ch[u][0],ch[u][1]);
        swap(f[u][0],g[u][0]);
        swap(f[u][1],g[u][1]);
    }
    void Inr(int u)
    {
        if(!u)return ;
        inr[u]^=1;
        v[u]=-v[u];sum[u]=-sum[u];
        swap(f[u][0],f[u][1]);
        swap(g[u][0],g[u][1]);
        f[u][0]=-f[u][0];f[u][1]=-f[u][1];
        g[u][0]=-g[u][0];g[u][1]=-g[u][1];
    }
    void Rep(int u,int d)
    {
        if(!u)return ;
        tag[u]=d;
        inr[u]=0;
        v[u]=d;
        if(d==1)
        {
            sum[u]=siz[u];
            f[u][0]=g[u][0]=siz[u];
            f[u][1]=g[u][1]=0;
        }else
        {
            sum[u]=-siz[u];
            f[u][0]=g[u][0]=0;
            f[u][1]=g[u][1]=-siz[u];
        }
    }
    void pushdown(int u)
    {
        int ls = ch[u][0],rs = ch[u][1];
        if(tag[u])
        {
            Rep(ls,tag[u]),Rep(rs,tag[u]);
            tag[u]=0;swa[u]=0;
        }
        if(swa[u])
        {
            Swap(ls),Swap(rs);
            swa[u]=0;
        }
        if(inr[u])
        {
            Inr(ls),Inr(rs);
            inr[u]=0;
        }
    }
    int st[N],tl;
    void down(int u)
    {
        tl=0;st[++tl]=u;
        while(fa[u])u=fa[u],st[++tl]=u;
        while(tl)pushdown(st[tl]),tl--;
    }
    void rotate(int x)
    {
        int y = fa[x],z = fa[y],k = (ch[y][1]==x);
        ch[y][k]=ch[x][!k],fa[ch[x][!k]]=y;
        ch[x][!k]=y,fa[y]=x;
        ch[z][ch[z][1]==y]=x,fa[x]=z;
        update(y),update(x);
    }
    void splay(int x,int goal)
    {
        down(x);
        while(fa[x]!=goal)
        {
            int y = fa[x],z = fa[y];
            if(z!=goal)
                (ch[z][1]==y)^(ch[y][1]==x)?rotate(x):rotate(y);
            rotate(x);
        }
        if(!goal)rt = x;
    }
    int get_pnt(int x,int k)
    {
        pushdown(x);
        int tmp = siz[ch[x][0]];
        if(k<=tmp)return get_pnt(ch[x][0],k);
        else if(k==tmp+1)return x;
        return get_pnt(ch[x][1],k-tmp-1);
    }
    int build(int l,int r,int f)
    {
        if(l>r)return 0;
        int x = (l+r)>>1;
        fa[x] = f;
        v[x] = (s[x]=='('?-1:1);
        ch[x][0] = build(l,x-1,x);
        ch[x][1] = build(x+1,r,x);
        update(x);
        return x;
    }
    void split(int &x,int &y)
    {
        x = get_pnt(rt,x);
        y = get_pnt(rt,y+2);
        splay(x,0);splay(y,x);
    }
    void _replace(int x,int y,int d)
    {
        split(x,y);
        Rep(ch[y][0],d);
        update(y),update(x);
    }
    void _swap(int x,int y)
    {
        split(x,y);
        Swap(ch[y][0]);
        update(y),update(x);
    }
    void _invert(int x,int y)
    {
        split(x,y);
        Inr(ch[y][0]);
        update(y),update(x);
    }
    int _query(int x,int y)
    {
        split(x,y);
        return (f[ch[y][0]][0]+1)/2+(-g[ch[y][0]][1]+1)/2;
    }
}tr;
char opt[20];
int main()
{
    scanf("%d%d%s",&n,&m,s+2);
    tr.rt=tr.build(1,n+2,0);
    for(int x,y,i=1;i<=m;i++)
    {
        scanf("%s%d%d",opt+1,&x,&y);
        if(opt[1]=='R')
        {
            scanf("%s",opt+1);
            int d = 1;
            if(opt[1]=='(')d=-1;
            tr._replace(x,y,d);
        }else if(opt[1]=='S')
        {
            tr._swap(x,y);
        }else if(opt[1]=='I')
        {
            tr._invert(x,y);
        }else
        {
            printf("%d\n",tr._query(x,y));
        }
    }
    return 0;
}